Dessinons une spirale de Fibonacci

• Le pourquoi du comment des lignes à haute tension
• Assemblée Générale Ordinaire 2016 de Zeste de Savoir

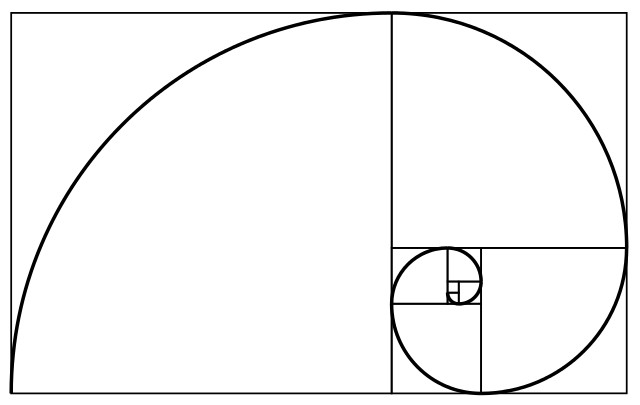
Tout le monde connait la célèbre suite de Fibonacci et sa spirale. Cette spirale est composée d’une série de quarts de cercles s’inscrivant chacun dans un carré. Ces carrés sont disposés selon un chemin qui tourne autour du centre de la spirale et recouvrent entièrement rectangle tendant à être d’or lorsque le nombre de carrés augmente. C’est de cette spirale dont il sera question dans cet article.

La spirale de Fibonacci parait être un motif particulièrement simple, voire simpliste : composée uniquement de quarts de cercles inscrit dans des carrés et agencés de manière régulière, le dessin à la main est particulièrement facile lorsqu’on connait quelques propriétés de celle-ci. Si dessiner une spirale de Fibonacci à la main est facile, comment s’y prendrait-on pour demander à un ordinateur de le faire lui-même ? Ce n’est plus aussi simple que de le faire soi-même si on désire automatiser cette tâche en ne se donnant comme point de départ que le nombre de carrés et la largeur du plus petit d’entre eux.

Dans cet article, je vais vous expliquer la construction d’un algorithme qui permet de dessiner une spirale de Fibonacci ainsi que ses carrés. Une fois cet algorithme implémenté, vous serez capable de produire une image analogue à la figure ci-dessous.

• La suite de Fibonacci
• Construction de l’algorithme de dessin
• Implémentation de l’algoritme et exemple

La suite de Fibonacci

La suite de Fibonacci se définit par récurrence : chaque terme est la somme des deux termes précédents. Si on note cette suite $(u_n)$ avec $n$ un entier naturel, alors $u_0=0$, $u_1=1$ et, pour tous les indices $n\geqslant2$, $u_n=u_{n-1}+u_{n-2}$. Les dix premiers termes de la suite de Fibonacci sont donc : 0, 1, 1, 2, 3, 5, 8, 13, 21 et 34.

Construction de l’algorithme de dessin

Analyse de la spirale de Fibonacci

Observons les étapes successives de la construction d’une spirale de Fibonacci en partant du premier carré. Posons $N$ comme étant le nombre maximal d’itérations, $n\leqslant N$ comme étant l’itération courante et définissons quelques points :

• $O$, le centre de la spirale et correspond au début de celle-ci ;
• $F_n$, l’extrémité de la spirale à l’étape $n$ ;
• $M_n$, le coin inférieur gauche du dernier carré à l’étape $n$ ;
• $C_n$, le coin inférieur gauche du rectangle à l’étape $n$ ;
• $P_n$, le centre de l’arc de cercle de l’étape $n$.

Les points $M_n$ et $C_n$ sont les origines des carrés et du rectangle et sont utilisés pour leur tracé. Le point $C_N$ permet de positionner l’ensemble du motif lors du tracé afin d’éviter que des points aient des coordonnées négatives ou de ne pas avoir à se soucier des coordonnées de $O$.

Considérons dès à présent que nous nous trouvons dans un repère orthonormé $(O, \vec{x}, \vec{y})$.

Les six images suivantes représentent l’évolution de la spirale pendant les six premières étapes. Les points correspondant à la dernière étape sont reportés.

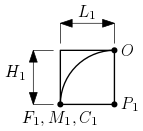
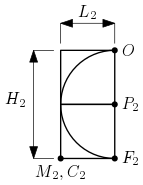
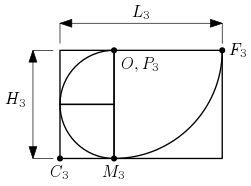
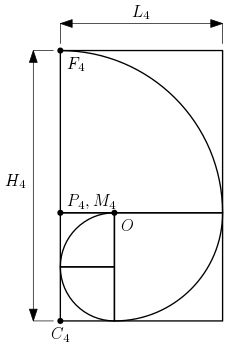
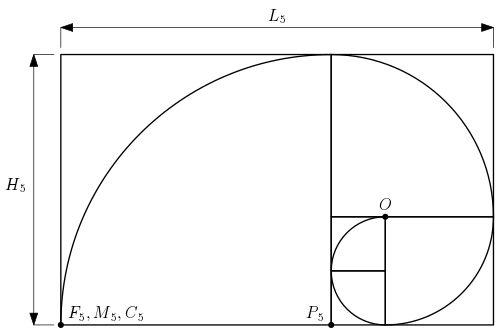
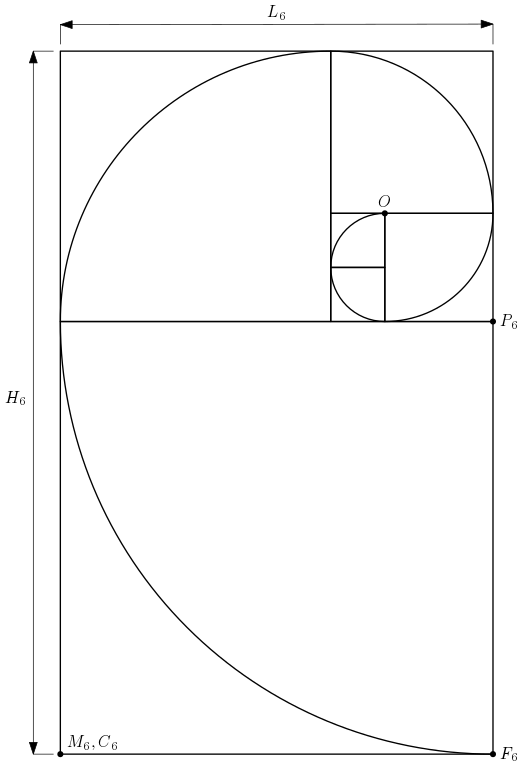
La spirale, partant du point $O$, traverse le premier carré de côté $u_1=1$ et arrive au point $F_1$ ; dans le deuxième carré (de côté $u_2=1$), la spirale part du point $F_1$ et arrive au point $F_2$ ; au $n$-ième carré (de côté $u_n$), la spirale part du point $F_{n-1}$ et arrive au point $F_n$.

À tout instant, la spirale s’inscrit dans un rectangle de largeur $L_n$ et de hauteur $H_n$. Si on considère l’orientation de l’image, alors la valeur de $L_n$ et de $H_n$ est :

La spirale en elle-même est composée de quarts de cercles centrés sur des points $P_n$. Les angles extrêmes $\theta^+_n$ et $\theta^-_n$ ont pour valeur des multiples de $\frac\pi2$ et on a toujours $\theta^+_n-\theta^-_n=\frac\pi2$. Dans le dessin, $\theta^-_1=\frac\pi2$. À chaque itération, les angles augmentent de $\frac\pi2$. Il est alors évident que :

et que

Pour calculer la position de tous les points pour toutes les valeurs de $n$, exprimons la position de $M_n$, $P_n$ et $C_n$ à partir de la position de $F_n$, celle-ci étant déterminé à partir de la position de $O$. Cela se fera en considérant les six premières itérations de la spirale.

Détermination de la position de l’extrémité de la spirale

Pour aller du point $O$ au point $F_1$, il faut se déplacer selon le vecteur $\overrightarrow{OF_1}+(-1,-1$). Pour aller du point $O$ au point $F_2$, il faut se déplacer selon le vecteur $\overrightarrow{OF_2}+\overrightarrow{OF_1}=(1,-1)$. Par suite : $\overrightarrow{OF_3}=\overrightarrow{OF_2}+(2,2)$ ; $\overrightarrow{OF_4}=\overrightarrow{OF_3}+(-3,3)$ ; $\overrightarrow{OF_5}=\overrightarrow{OF_4}+(-5,-5)$ ; $\overrightarrow{OF_6}=\overrightarrow{OF_5}+(8,-8)$.

En divisant chaque vecteur par la valeur de la suite de Fibonacci, les coordonnées des vecteurs ajoutés successivement sont toujours égales à 1 en valeur absolue :

Finalement, si on trace l’évolution des coordonnées de $\frac1{u_n}\overrightarrow{F_{n-1}F_n}$ en fonction de $n$ sachant que $\frac1{u_n}\overrightarrow{F_0F_1}=\overrightarrow{OF_1}=(-1,-1)$, on obtient ceci :

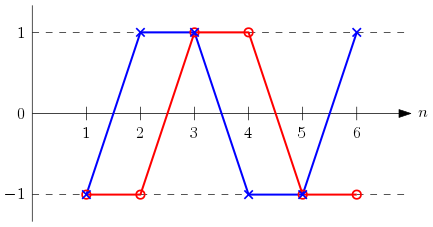
Pour connaître la valeur des coordonnées du vecteur $\overrightarrow{OF_n}$ pour toutes les valeurs de $n$, il faut trouver une fonction qui rend compte des variations de $\frac1{u_n}\overrightarrow{F_{n-1}F_n}$. On peut exprimer les variations de $\frac1{u_n}\overrightarrow{F_{n-1}F_n}$ selon $\vec y$ avec la même fonction mais en décalant $x$ de 1. La fonction qu’il faut construire devrait être périodique et son amplitude devrait être constante. Cela ressemble à un sinus ou à un cosinus. Introduisons la fonction $f$ telle que :

avec $a$, $b$ et $c$ des réels à déterminer. Il s’agit d’un cosinus dont on peut faire varier l’amplitude, la période et le décalage par rapport à $x=0$. Démontrons que $f$ permet de rendre compte des variations de $\frac1{u_n}\overrightarrow{F_{n-1}F_n}$ :

Pour que $f$ puisse rendre compte des variations de $\frac1{u_n}\overrightarrow{F_{n-1}F_n}$ selon $\vec x$, il faut que :

De plus, il faut que la dérivée de $f'(\frac12)=0$. Comme $f'(x)=-ab\sin(bx+c)$ :

Connaissant ce résultat, on sait maintenant que $a\cos-c=a\cos c=-1$, $a\cos(-3c)=a\cos(3c)=1$. Or $\cos x=\sin\left(\frac\pi2-x\right)$ et $\sin(-x)=-\sin x$. On a donc :

et :

On peut alors dire que :

Donc :

La condition $a\cos c=-1$ donne immédiatement $a=-\sqrt2$.

Donc $f(x)=-\sqrt2\cos\left(\frac\pi2\left(\frac12-x\right)\right)$. On a donc $\frac{1}{u_n}\overrightarrow{F_{n-1}F_n}=f(n)$, soit :

Détermination de la position de l’origine des carrés

Pour déterminer la position de $M_n$, procédons de la même manière que précédement mais, au lieu de partir de $O$, partons de $F_n$ et analysons les variations du vecteur $\overrightarrow{F_nM_n}$ :

Traçons l’évolution des coordonnées de $\frac1{u_n}\overrightarrow{F_nM_n}$ en fonction de $n$ :

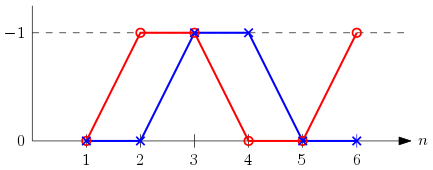
L’évolution est semblable à celle du vecteur $\overrightarrow{F_{n-1}F_n}$. En réalité, on peut exprimer $\overrightarrow{F_nM_n}$ en fonction de $f$ :

avec $g(x)= \frac12(1+f(x))$. Ce qui donne :

Détermination de la position du centre des arcs

Analysons les variations du vecteur $\overrightarrow{F_nP_n}$ :

Traçons l’évolution de $\frac1{u_n}\overrightarrow{F_nP_n}$ en fonction de $n$ :

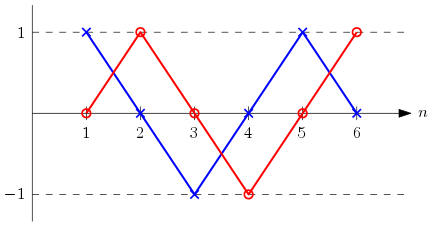
$\overrightarrow{F_nP_n}$ dépend directement de l’angle $\theta^-_n$ :

Détermination de la position de l’origine du rectangle circonscrit

Analysons les variations du vecteur $\overrightarrow{F_nC_n}$ :

Traçons l’évolution des coordonnées de $\overrightarrow{F_nM_n}$ en fonction de $n$. Cette fois-ci, les coordonnées selon $\vec x$ sont divisées par $L_n$ et les coordonnées selon $\vec y$ sont divisées par $H_n$.

On retrouve exactement la même évolution que celle de $\overrightarrow{F_nM_n}$. Cela signifie que :

Mise en place de l’algorithme de dessin

La position de tous les points a été déterminée. Nous pouvons maintenant établir l’algorithme de dessin de la spirale de Fibonacci. Les variables utilisées sont :

• N : nombre maximal de carrés ;
• largeur_unité : largeur du plus petit carré ;
• origine_spirale_x et origine_spirale_y : coordonnées du point $O$ ;
• fin_spirale_x et fin_spirale_y : coordonnées des points $F_n$ ;
• coin_carré_x et coin_carré_y : coordonnées des points $M_n$ ;
• coin_ext_x et coin_ext_y : coordonnées des points $C_n$ ;
• centre_arc_x et centre_arc_y : coordonnées des points $P_n$ ;
• angle_min et angle_max : angles limites des arcs de cercle.

Il est utile de définir préalablement quelques fonctions. La première et la plus importante est celle qui calcule les différents termes de la suite de Fibonacci et qui est appelée fibonacci. Une implémentation de fibonacci peut-être réalisée simplement en utilisant la récursivité :

1
2
3
4
5
6
7

Fonction fibonacci(n)
    Si n <= 1 alors
        Retourner n
    Sinon
        Retourner fibonacci(n - 1) + fibonacci(n - 2)
    Fin si
Fin fonction

La largeur $L_n$ et la hauteur $H_n$ peuvent être définies comme suit :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

Fonction L(n)
    Si n est pair alors
        Retourner fibonacci(n)
    Sinon
        Retourner fibonacci(n + 1)
    Fin si
Fin fonction

Fonction H(n)
    Si n est pair alors
        Retourner fibonacci(n + 1)
    Sinon
        Retourner fibonacci(n)
    Fin si
Fin fonction

Les fonctions $f$ et $g$ se traduisent directement :

1
2
3
4
5
6
7

Fonction f(n)
    Retourner sqrt(2)*cos((pi/2)*(1/2 - n)
Fin fonction

Fonction g(n)
    Retourner (1/2 - 1/sqrt(2))*cos((pi/2)*(1/2 - n))
Fin fonction

L’algorithme suivant traduit le raisonnement mathématique effectué précédemment. Les carrés et les arcs peuvent soit être tracés au fur-et-à-mesure soit être tracés tous ensemble après avoir calculé et stocké les coordonnées de tous les points.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

Pocédure dessin_spirale(N, largeur_unité, origine_spirale_x, origine_spirale_y)
    fin_spirale_x := origine_spirale_x
    fin_spirale_y := origine_spirale_y

    Pour n allant de 1 à N: {1 et N sont inclus}
        fin_spirale_x := fin_spirale_x - largeur_unité*fibonacci(n)*f(n)
        fin_spirale_y := fin_spirale_x - largeur_unité*fibonacci(n)*f(n - 1)

        coin_carré_x := fin_spirale_x - largeur_unité*fibonacci(n)*g(n)
        coin_carré_y := fin_spirale_y - largeur_unité*fibonacci(n)*g(n - 1)

        coin_ext_x := fin_spirale_x - largeur_unité*L(n)*g(n)
        coin_ext_y := fin_spirale_y - largeur_unité*H(n)*g(n - 1)

        centre_arc_x := fin_spirale_x + largeur_unité*fibonacci(n)*sin(n*pi/2)
        centre_arc_y := fin_spirale_y - largeur_unité*fibonacci(n)*cos(n*pi/2)

        angle_min = n*pi/2
        angle_max = angle_min + pi/2
    Fin pour
Fin procédure

Pour positionner la spirale à partir du point $A$ (qui sera confondu avec $C_N$) dont les coordonnées sont stockées dans les variables origine_x et origine_y, il y a deux approches. La première est de parcourir l’algorithme ci-dessus et de stocker séparément les coordonnées, puis, connaissant les valeurs extrêmes de coin_ext_x et de coin_ext_y, d’effectuer le calcul suivant :

1
2
3
4

Pour tous les points Q
    q_x := q_x - max(coin_ext_x) + origine_x
    q_y := q_y - max(coin_ext_y) + origine_y
Fin pour

La deuxième approche est de déterminer à l’avance la position du point $C_n$ et d’initialiser origine_spirale_x et origine_spirale_y en fonction de ses coordonnées :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

fin_spirale_x := 0
fin_spirale_y := 0

coin_ext_x := 0
coin_ext_y := 0

Pour n allant de 1 à N
    fin_spirale_x := fin_spirale_x - largeur_unite*fibonacci(n)*f(x)
    fin_spirale_y := fin_spirale_y - largeur_unite*fibonacci(n)*f(x - 1)

    coin_ext_x := fin_spirale_x - largeur_unite*L(n)*g(n)
    coin_ext_y := fin_spirale_y - largeur_unite*H(n)*g(n - 1)
Fin pour

origine_spirale_x := origine_x - coin_ext_x
origine_spirale_y := origine_y - coin_ext_y

Passons maintenant à l’implémentation de l’algorithme.

Implémentation de l’algoritme et exemple

Ci-dessous, je vous propose une implémentation dans l’environnement Processing. Processing est un environnement de programmation graphique qui peut utiliser plusieurs syntaxes différentes. La syntaxe utilisée ici est celle du langage Python.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

def L(n):
    if n%2 == 0:
        return fibonacci(n)
    else:
        return fibonacci(n + 1)

def H(n):
    if n%2 == 0:
        return fibonacci(n + 1)
    else:
        return fibonacci(n)

largeur_unite = 10
ordre_max = 7

# Vecteur OF
fin_spirale_x, fin_spirale_y = 0, 0

# Vecteur OC = OF + FC
coin_ext_x, coin_ext_y = 0, 0

# Calcul de la position du coin inférieur gauche de la spirale.
for n in range(1, ordre_max + 1):
    fin_spirale_x -= sqrt(2)*largeur_unite*fibonacci(n)*cos(HALF_PI*(0.5 - n))
    fin_spirale_y -= sqrt(2)*largeur_unite*fibonacci(n)*cos(HALF_PI*(1.5 - n))

    coin_ext_x = fin_spirale_x - largeur_unite*L(n)*(0.5 - (1/sqrt(2))*cos(HALF_PI*(0.5 - n)))
    coin_ext_y = fin_spirale_y - largeur_unite*H(n)*(0.5 - (1/sqrt(2))*cos(HALF_PI*(1.5 - n)))

# Application du décalage.
fin_spirale_x, fin_spirale_y = -coin_ext_x, -coin_ext_y

# Dessin du cadre.
rect(0, 0, largeur_unite*L(ordre_max), largeur_unite*H(ordre_max))

for n in range(1, ordre_max + 1):
    # Vecteur OF
    fin_spirale_x -= sqrt(2)*largeur_unite*fibonacci(n)*cos(HALF_PI*(0.5 - n))
    fin_spirale_y -= sqrt(2)*largeur_unite*fibonacci(n)*cos(HALF_PI*(1.5 - n))

    # Vecteur OM = OF + FM
    coin_carre_x = fin_spirale_x - largeur_unite*fibonacci(n)*(0.5 - (1/sqrt(2))*cos(HALF_PI*(0.5 - n)))
    coin_carre_y = fin_spirale_y - largeur_unite*fibonacci(n)*(0.5 - (1/sqrt(2))*cos(HALF_PI*(1.5 - n)))

    # Vecteur OC = OF + FC
    coin_ext_x = fin_spirale_x - largeur_unite*L(n)*(0.5 - (1/sqrt(2))*cos(HALF_PI*(0.5 - n)))
    coin_ext_y = fin_spirale_y - largeur_unite*H(n)*(0.5 - (1/sqrt(2))*cos(HALF_PI*(1.5 - n)))

    # Vecteur OP = OF + FP
    centre_arc_x = fin_spirale_x + largeur_unite*fibonacci(n)*sin(HALF_PI*n)
    centre_arc_y = fin_spirale_y - largeur_unite*fibonacci(n)*cos(HALF_PI*n)

    angle_min = n*HALF_PI
    angle_max = angle_min + HALF_PI

    rect(coin_carre_x, coin_carre_y, largeur_unite*fibonacci(n), largeur_unite*fibonacci(n))
    arc(centre_arc_x, centre_arc_y, 2*largeur_unite*fibonacci(n), 2*largeur_unite*fibonacci(n), angle_min, angle_max)

Résultat avec $N=7$ :

On constate que la spirale tourne dans le sens des aiguilles d’une montre alors que l’étude a été effectuée avec une spirale tournant dans le sens trigonométrique. Cette différence s’explique par le repère utilisé par Processing et les ordinateurs en général. En mathématiques, l’origine d’un repère est généralement située en bas à gauche et l’axe $\vec y$ est dirigé vers le haut. En informatique, l’origine est située en haut à gauche et l’axe $\vec y$ est dirigé vers le bas.

Nous venons de voir la construction d’un algorithme de dessin de la spirale de Fibonacci. Il vous permettra de réaliser facilement ces spirales à chaque fois que vous en aurez besoin. Il est facilement adaptable et la technique utilisée pour le dessin lui-même peut grandement varier : du pixel-art, du dessin vectoriel, etc. À ce titre, je vous invite à générer quelques spirales originales et à les montrer en commentaire.

L’algorithme présenté n’est pas le seul possible : n’hésitez-pas à en présenter de nouveaux dans les commentaires.

• Le pourquoi du comment des lignes à haute tension
• Assemblée Générale Ordinaire 2016 de Zeste de Savoir