Fonction logistique

Salut !

Je m'intéresse actuellement aux fonctions logistiques définies par

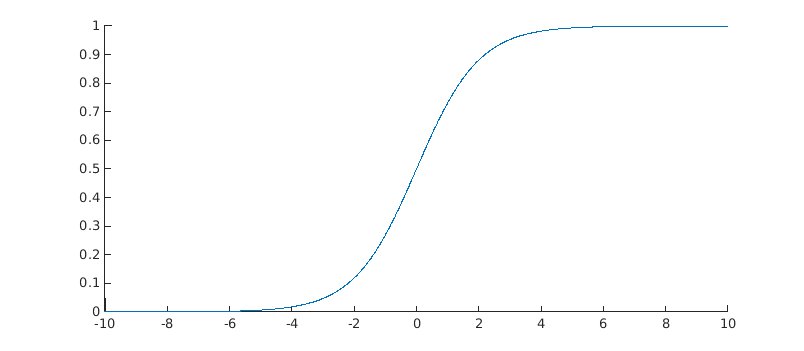
Ma question c'est : comment réussir à créer une fonction sigmoïde comprise entre $1 > y_0 >0$ et ayant un "plateau proche de 0". En image :

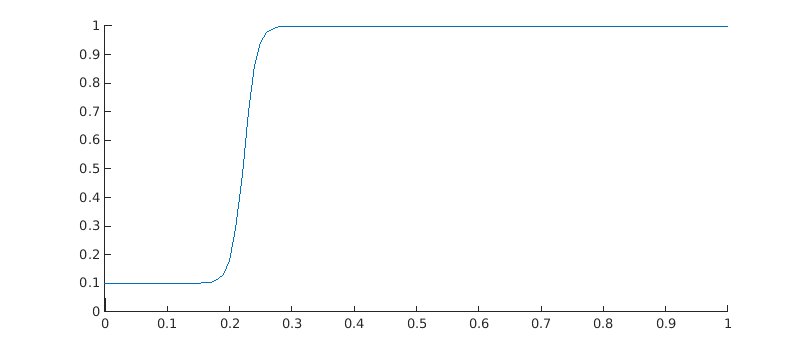
J'ai obtenu ca en bidouillant $\lambda$ et $a$ (ici 100 et 10 respectivement) ainsi qu'en calculant pour $X = x-0.2$ (décale à droite) et en faisant finalement $ y_2 = y*(1-y0) + y0 $ pour décaler verticalement.

Seulement : - C'est pas propre comme façons de faire. - Je peux pas régler tout comme je veux, c'est du bidouillage.

Du coup, est-ce que vous voyez un moyen propre de faire tout ca ? L'idée serait qu'à la fin je fasse un script avec en entrée l'ordonnée à l'origine, l'abscisse du point d'inflexion et un "indice de pente" (qui lui est déterminé par $\lambda$). J'y suis presque, sauf pour l'abscisse du point d'inflexion.

Tu utilises quel langage ?

Ma question c'est : comment réussir à créer une fonction sigmoïde comprise entre 1>y0>0

y0, c'est ta fonction ?

et ayant un "plateau proche de 0"

Tu parles du morceau qui part de 0.1 ?

On y verrait plus clair si tu nous expliquais pourquoi tu veux faire ça.

Désolé je suis pas rigoureux $ y_0 $ c'est l'ordonnée à l'origine, le plateau c'est bien ce qui part de 0.1.

J'essaie de rendre compte d'un phénomène qui a 2 seuils : l'évaporation du sol en fonction de son contenu en eau. Tout d'abord l'évaporation est limité par le rayonnement solaire arrivant, puis au bout d'un temps par la vitesse de déplacement de la vapeur d'eau. Or je n'ai pas envie de résoudre le déplacement de la vapeur d'eau dans le sol… Or pour un phénomène à 2 phases la sigmoïde est bien adaptée. Quand je teste sur des données ca correspond pas mal aux observations, seulement j'essaie d'affiner.

J'utilise Matlab pour faire ca, mais ca ne devrait pas changer grand chose, c'est la partie mathématique qui m'intéresse là.

Salut,

Logiquement, en prenant $x-0.2\to x$ comme tu l'as fait, tu décales bien la courbe de façon rigide et donc l'abscisse du point d'intersection est à $0.2$.

Pour la compression verticale, j'aurais tendance à calculer $0.9y+0.1$. Si j'ai bien compris, c'est ce que tu as fait aussi. Mais du coup, je ne comprends pas ce qu'il te manque.

J'aimerais pouvoir spécifié l'abscisse du point d'inflexion. Or pour l'instant le $x - 0.2 \rightarrow x$ décale pas comme il faut. Normalement $y(0)=0.5=y_{1/2}$ au point d'inflexion. Je comprend assez bien que la compression verticale fasse que le "$y_{1/2}$" après transformation ne soit plus 0.5, mais par contre je comprend pas pourquoi il n'est pas en $x=0.2$, mais plutôt en $x=0.25$ visiblement.

Je vais potasser tout ca, notamment en faisant proprement avec dérivée, dérivée seconde et tout…

Il y a un truc que je pige pas, c'est pourquoi tu t'attends à ce que le point d'inflexion soit en $x=0$ avec la fonction de base. À vue de nez, il faut $a=1$ pour que ce soit le cas.

Yep… J'ai cafouillé là… En faite j'ai mélangé 2 trucs. Au début j'avais pas décaler en ordonnées avec le $0.9y +0.1$, je le faisant à la louche en changeant $a$ car la fonction logistique admet comme ordonnée à l'origine $y(0)=y_0$ qui est lié à $a$.

Les fonctions logistiques doivent résoudre : \begin{cases}
y' &=\lambda y\left(1-\frac yK\right) \newline y(0) &= y_0 \end{cases}

Les solutions sont les fonctions $f$ tel que

donc $a = K/y_0 -1$. Mais toujours est-il que maintenant j'en ai plus besoin.

Merci de m'avoir fait prendre du recul sur le truc