La représentation intervallaire

Gestion d'arbre en SQL

Une notion bien étrange que voilà…

Mettons nous en situation, sur un système de forums, ayant plusieurs niveaux. Chaque forum peut posséder un parent et des enfants. Pour naviguer dans ce type d’arborescence, vous procéderez probablement par des héritages ditsrécursifs, caractérisés par une colonne parent_id, méthode également connue sous le terme peu barbare de représentation classique ou représentation récursive, en renseignant de manière récursive la clause WHERE, en utilisant des sous-requêtes ou bien des jointures… Ou des concepts plus avancés que je n’aborderai pas ici.

Mais cela peut très vite devenir lourd… et peu pratique, surtout à partir d’un certain niveau, comme nous le verrons par la suite.

Dans ce tuto, nous allons donc voir comment éviter cette lourdeur en employant une "ruse" mise au point par les développeurs : la représentation par arbre d’intervalle.

Accrochez-vous, on y va !

La Théorie

Une (petite) présentation du schmilblick

Avant d’attaquer la bête, nous avons, tout d’abord, besoin de la définir. Tout d’abord, qu’est-ce que la repr…

C’est vrai ça, c’est quoi la rapré… représentation invert… cette chose ?

La représentation intervallaire !

Cette technique peut permettre de situer un élément dans une hiérarchie. Pour donner une image de cette notion de hiérarchie, prenons l’exemple d’un système de forums.

Un tel système peut proposer $[1,\infty[$ catégories, elles-même composées de $[0,\infty[$ forums, eux-mêmes pouvant être composés de $[0,\infty[$ sous-forums. Voilà ce qu’est la notion de hiérarchie : si je suis dans un sous-forum, qui lui est donc dans un forum, lui-même dans une catégorie, ça veut dire que je suis à la troisième hiérarchie. Il peut, bien entendu, y avoir plusieurs éléments ayant le même niveau, comme, toujours à l’image d’un système de forums, plusieurs forums affiliés à une catégorie.

Un point essentiel – si ce n’est le plus important ! – à retenir dans la représentation intervallaire (je ne vois pas ce qu’il y a de compliqué à retenir là-dedans, ce n’est quand même pas de l’acide acétyli… acide acytéli… bref, un certain médicament…), c’est la notion de borne gauche, borne droite. Voici un schéma1 pour illustrer cette notion :

Concept de la RI

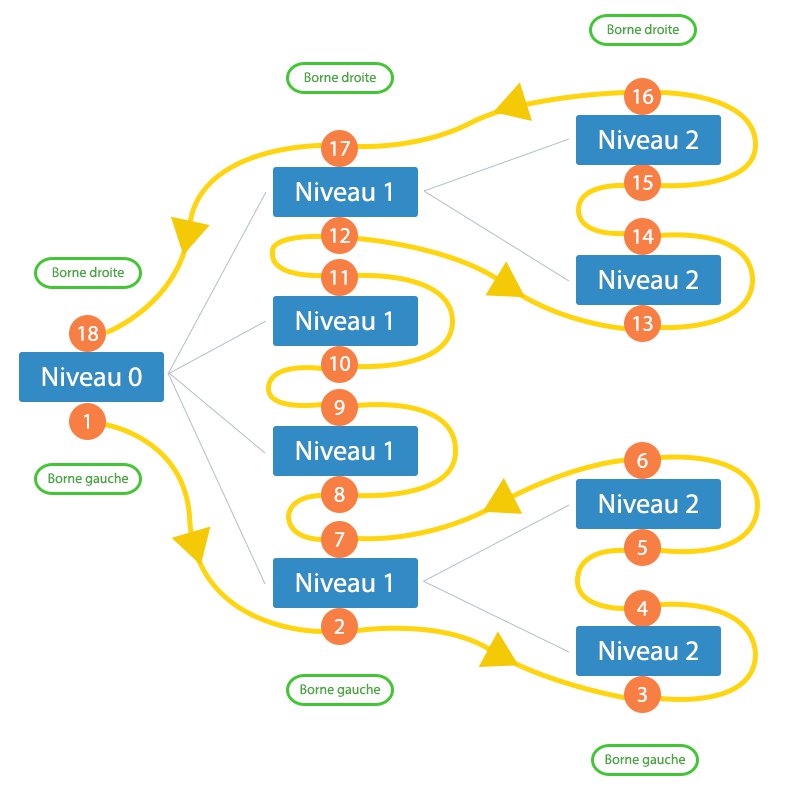
Comme vous pouvez le voir, chaque borne de chaque élément se voit attribuer un nombre. Ce nombre permet de déterminer la position de l’élément dans l’ensemble. Notez également que la borne gauche est toujours inférieure à la borne droite. Notez bien ce point, il est très important  !

À propos de points importants, j’en profite pour présenter un autre aspect de la représentation intervallaire : il existe plusieurs type de nœud, deux pour être plus précis. Soit il s’agit d’un nœud dit "nœud complexe" (ou sous-arbre), qui comprend donc des nœuds fils, soit il peut s’agir d’une feuille, qui, à l’image d’un arbre, ne sera qu’un simple élément, et ne comporte pas de descendance quelconque.

Pour identifier mathématiquement les deux, il faut juste calculer la différence entre la borne droite et la borne gauche. Si le résultat est égal à 1, il s’agit d’une feuille, sinon d’un nœud. On peut même pousser le raisonnement un peu plus loin : cette différence nous donne le double nombre d’enfants de ce nœud auquel on lui rajoute un. Vérifions-le pour une feuille (disons le nœud ayant les bornes 3 et 4) :

$$ \begin{array} {lcl} \text{borne droite} - \text{borne gauche} & = & 4 - 3 \\\ & = & 1 \\\ & = & 0 + 1 \\\ & = & \boxed{0} \times 2 + 1 \end{array}$$

Le nœud aux bornes 3 et 4 est donc une feuille, et ne comporte donc aucun élément fils. Vérifions le également pour un des nœuds du premier niveau du schéma, celui ayant les bornes 2 et 7 :

$$\begin{array} {lcl} \text{borne droite} - \text{borne gauche} & = & 7 - 2 \\\ & = & 5 \\\ & = & 4 + 1 \\\ & = & \boxed{2} \times 2 + 1 \end{array}$$

La différence des bornes de ce nœud est donc supérieure à 1 : il s’agit donc d’un nœud "complexe". On s’aperçoit également qu’il comporte 2 enfants, ce qui est vérifiable sur le schéma.

Passons maintenant à la préparation pour pouvoir pratiquer dans les deux parties suivantes de ce tutoriel. Je montrerai également pourquoi il est difficile (et coûteux) d’utiliser les "auto-jointures" – soit l’utilisation avec abus de la clause WHERE, des sous-requêtes et des jointures – pour accéder aux différents nœuds… Et qu’à moins d’avoir des idées tordues, cela devient vite impraticable.

NB : Dans cette sous-partie, je considère que vous avez un minimum de connaissances en SQL. Sinon, vous avez un bon tutoriel sur le SQL2 par Taguan que je ne peux que vous recommander.

La représentation intervallaire versus l’héritage récursif

L’héritage récursif ? Quelle prise de tête…

Voici la table type que nous allons utiliser pour illustrer (la faiblesse de) l’héritage récursif :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
CREATE TABLE tuto_herit (
        id mediumint(8) NOT NULL AUTO_INCREMENT,
        parent_id mediumint(8) DEFAULT NULL,
        /* ... */

        PRIMARY KEY  (id),
        KEY parent_id (parent_id)
    );

INSERT INTO tuto_herit (id, parent_id)
    VALUES
        (1, NULL),
        (2, 1),
        (3, 2),
        (4, 2),
        (5, 1),
        (6, 1),
        (7, 1),
        (8, 7),
        (9, 7)/*,[...]*/;

À partir du nœud portant l’id n°8, comment faire, à l’aide des jointures, pour accéder à l’ensemble de ses parents ? Vous ne devez, bien entendu, n’avoir qu’un seul parent par ligne (pas tous, sinon ce serait trop facile, surtout si on connaît la profondeur du nœud !).

…

…

Vous n’y arrivez pas ? Pour tout vous avouer, moi non plus ! Ici, on peut facilement avoir tous les parents sur la même ligne à l’aide de quelques jointures (en utilisant l’héritage de la colonne parent_id) ; or, ce n’était pas ce qui était demandé : on voulait un nœud par ligne. Certes, les jointures, c’est pratique, mais à la longue… c’est vite pesant et peu pratique.

NB : pour les curieux qui veulent absolument résoudre ce problème, une piste serait d’utiliser une procédure récursive pour trouver ce qu’on cherche, mais ça reste consommateur de ressources si l’arbre est trop profond (dans notre cas, cela peut être considéré comme trop profond). Mais ce sujet ne nous intéresse pas ici.

La représentation intervallaire ? Yeah !

Reprenons la première table, et adaptons-la dans un arbre :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
CREATE TABLE tuto_ri (
        id mediumint(8) NOT NULL AUTO_INCREMENT,
        node_depth mediumint(8) NOT NULL DEFAULT 0,
        node_left mediumint(8) NOT NULL,
        node_right mediumint(8) NOT NULL,
        /* ... */

        PRIMARY KEY  (id),
        KEY node (node_left, node_right)
    );

INSERT INTO tuto_ri (id, node_depth, node_left, node_right)
    VALUES
        (1, 0, 1, 18),
        (2, 1, 2, 7),
        (3, 2, 3, 4),
        (4, 2, 5, 6),
        (5, 1, 8, 9),
        (6, 1, 10, 11),
        (7, 1, 12, 17),
        (8, 2, 13, 14),
        (9, 2, 15, 16)/*,[...]*/;

Allez, même exercice que tout à l’heure : recherchez l’id et la hiérarchie des nœuds parents de la feuille ayant l’id "8", ayant pour bornes 13 et 14, en les triant du parent le plus proche au parent le plus lointain !

…

…

…

…

Ah, c’est vrai, j’avais oublié le petit indice : utilisez les bornes des nœuds. Si vous n’aviez pas deviné, ce n’est pas grave, voici ma solution, et pour tenter de me faire pardonner, je l’ai commentée pour que vous la compreniez mieux.

1
2
3
4
5
SELECT id, node_depth
    FROM tuto_ri
    WHERE node_left < 13
        AND node_right > 14
    ORDER BY node_depth DESC;

On cherche à récupérer l’ID, le nom, et la hiérarchisation des nœuds parents, ce qu’on fait en sélectionnant les champs id, name, et node_depth. Ensuite, dans la clause WHERE, on applique un des points principaux de la représentation intervallaire : la borne gauche d’un nœud est toujours plus grande que celle des nœuds parents. On sélectionne donc tous les nœuds ayant, dans notre cas, une borne gauche plus petite que 7. On applique la même chose à la borne droite, sauf que cette fois-ci, la borne droite de la feuille est toujours plus petite que celle des nœuds parents.

On a donc les nœuds que l’on désire… Mais ce n’est pas fini, il y avait un petit piège : on souhaite avoir les nœuds… Du plus proche au plus lointain par rapport à la feuille. Il suffisait juste d’ajouter une petite clauseORDER BY, en indiquant le nom de la colonne qui sert à trier (node_depth), et par ordre décroissant. Je vous avais bien dit que la notion de hiérarchisation pouvait s’avérer utile par moments… En voilà la preuve même !

id node_depth
7 1
1 0

NB : Notez que si je vous avais demandé, dans la liste des nœuds ressortie, de ressortir également le nœud dans lequel on est, à la place des opérateurs < et >, il faudrait alors utiliser <= et >=.

1
2
3
4
5
SELECT id, node_depth
    FROM tuto_ri
    WHERE node_left <= 13
        AND node_right >= 14
    ORDER BY node_depth DESC;
id node_depth
8 2
7 1
1 0

Dans les deux parties qui suivent, nous allons voir les différentes techniques et opérations chirurgicales liées à la représentation intervallaire, telles que…

  • le comptage du nombre d’éléments dans un nœud (que ce soit le nombre d’enfants, de parents, d’éléments…) ;
  • la modification du statut d’un élément, par l’ajout ou la suppression de nœuds ;
  • la possibilité de mettre à jour les indices aux bornes en fonction du nombre d’éléments

Ces deux parties agiront donc par plusieurs séries de "mini-TP", qui demandent par moments de la réflexion, et par moments des astuces… Bien évidemment, je vous guiderai pas à pas pour la réalisation de ces TP.

  1. Réalisé par Alex-D ↩

  2. Administrez vos bases de données avec MySQL ↩

La pratique : comptons !

Dans cette première (courte) série de TP, et afin de se mettre en jambes pour la seconde série, nous allons voir comment compter le nombre d’éléments d’un nœud, le nombre de feuilles d’un nœud, le nombre de nœuds "complexes" dans un même nœud, … bref, on va compter.

Compter le nombre d’éléments d’un nœud

Pour compter le nombre d’éléments d’un nœud, ça va être relativement simple, et vite expédié. Vous vous souvenez, à la fin de la première partie, on a vu comment récupérer tous les parents d’un nœud (et leur caractéristiques), en incluant ou non l’élément… Ici, ça va plus ou moins être le même topo.

Ce qui change, c’est que vous aurez besoin, comme je l’ai dit, non pas de sélectionner les parents de l’élément, mais ses enfants ! Donc, au lieu de rechercher tous les éléments qui ont une borne gauche inférieure à celle de l’élément recherché, et une borne droite supérieure à celle de l’élément, on va faire l’inverse.

On va essayer de compter le nombre d’enfants pour le nœud ayant l’id n°1 (le nœud racine) :

1
2
3
4
SELECT COUNT(*)
    FROM tuto_ri
    WHERE node_left > 1
        AND node_right < 18;

Vous avez vu, ce n’était pas si sorcier, il suffisait donc juste d’inverser les signes pour les deux bornes pour obtenir les enfants et non pas les parents du nœud, et d’utiliser la fonction d’agrégat COUNT(*). On trouve alors 8 éléments ; dans le sens inverse (en comptant donc les parents du nœud portant l’id n°2), on ne devrait trouver aucun parent.

Compter le nombre de feuilles d’un nœud

Mais… Mais… N’est-ce pas la même chose que ce qu’on a fait à l’instant même ?

Pas tout à fait ; ici, on ne cherchera pas à compter toute la filiation d’un nœud, mais en prenant également en compte le type de nœud (le nombre de feuilles ou de nœuds donc) d’un nœud.

Donc, on va à peu près procéder de la même manière qu’auparavant, mais tâchez juste de vous rappeler l’un des points à retenir de la représentation intervallaire. Vous y êtes ? Non ? Vous savez ce qu’il vous reste à faire…

1
2
3
4
5
SELECT COUNT(*)
    FROM tuto_ri
    WHERE node_left > 1
        AND node_right < 18
        AND (node_right - node_left) = 1;
COUNT(*)
6

Ce TP était également plutôt facile ; il suffisait de se souvenir que pour toutes les feuilles d’un arbre, la différence entre les deux bornes est toujours égale à 1. De même, pour compter le nombre de nœuds fils, vous pouvez, je pense, aisément le deviner : il faut chercher non pas les fils ayant une différence entre leurs bornes égale à 1, mais strictement supérieure à 1.

1
2
3
4
5
SELECT COUNT(*)
    FROM tuto_ri
    WHERE node_left > 3
        AND node_right < 24
        AND (node_right - node_left) > 1;
COUNT(*)
2

NB : Vous vous en doutez, un nœud ne peut avoir de feuilles comme parentes, ou c’est qu’il y alors un problème dans vos branches… Tout comme le calcul du nombre d’éléments parents donnera le même résultat que celui du calcul du nombre des nœuds parents. De plus, si vous additionnez le résultat du décompte des feuilles enfantes et des nœuds enfants du nœud recherché, on trouve alors le même résultat que celui du premier exercice.

Nous avons fini de tout compter, nous allons passer maintenant à quelque chose de bien plus intéressant : la modification d’un arbre. Que ce soit pour ajouter ou supprimer un nœud, ou même le déplacer, effectuer ces tâches n’est pas une mince affaire : on verra un poil d’algorithmie avant d’attaquer…

Manipulation de noeuds

Ici, on va voir comment mettre à jour un élément : mettre ses bornes à jour (ajout / suppression d’éléments), déplacement de nœuds… Bref, on va s’amuser à mettre à jour notre arbre.

Dans cette partie du tutoriel, nous allons voir quelques concepts intéressants, nous montrerons qu’en fait notre arbre est loin d’être immuable : nous pouvons rajouter ou enlever des nœuds, et même les déplacer ! Nous verrons d’abord l’ajout et la suppression, actions nécessaires pour bien comprendre le déplacement ensuite, qui lui est assez complexe et peut être divisé en plusieurs sous-parties, que nous aborderons alors en temps et en heure.

Ajout et/ou suppression d’éléments

Le cas des feuilles

Avant de s’amuser à pouvoir véritablement insérer ou retirer des nœuds dans le sens général du terme, regardons un peu comment le faire dans un cas un peu plus particulier, celui des feuilles. Celui-ci demande moins de réflexion, mais est tout de même assez intéressant pour comprendre le concept derrière la modification d’un arbre.

On va donc insérer une nouvelle feuille au nœud ayant l’id N°5. Même si dans ce cas très précis, on connaît déjà la borne gauche (8) et la borne droite (9) de cet élément, nous allons tout de même nous mettre dans un cas réel où ces deux bornes ne sont en général pas encore connues ; il nous faut alors les récupérer via une requête de type SELECT. En général, seule la sélection de la borne droite et – si on suit l’architecture, qui, je le rappelle, est facultative – de la profondeur suffit.

On aura également besoin de faire 2 requêtes UPDATE : changer les bornes droites puis les gauches de tous les éléments à partir desquels on souhaite insérer la nouvelle feuille. Donc, à chacun des nœuds concernés par cette modification (donc la feuille ayant l’id n°5 et les suivantes), on va incrémenter tout d’abord leur borne droite de 2, puis la borne gauche de 2 également. Faire ici deux requêtes nous évitera d’avoir une incohérence dans les bornes de nos tables. Une explication sur "pourquoi ajouter 2" viendra lorsque nous aborderons le cas des nœuds en général.

Enfin, on insère la nouvelle feuille par la droite. Pourquoi ? Lorsqu’on insère un élément, par pure logique, il est préférable de d’abord faire de la place pour celui-ci, et pour ne pas avoir de bornes négatives, on pousse alors les éléments qui seront situés après le nôtre vers la droite, pour qu’aucune borne ne puisse être négative, risquant ainsi d’invalider notre arbre au milieu de notre transaction.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
SELECT node_right, node_depth
    FROM tuto_ri
    WHERE id = 5;

/*
 * Ainsi, on sait que node_right vaut 9 et que la profondeur est de 1 ; tous les
 * éléments ayant une borne gauche et une borne droite supérieures à 9 seront
 * mis à jour par les deux requêtes qui suivent.
 *
 * Notre feuille aura alors comme borne 9 et 9+1 = 10, et aura pour profondeur
 * node_depth + 1 = 1 + 1 = 2.
 */

UPDATE tuto_ri
    SET node_right = node_right + 2
    WHERE node_right >= 9;

UPDATE tuto_ri
    SET node_left = node_left + 2
    WHERE node_left >= 9;

INSERT INTO tuto_ri (node_depth, node_left, node_right)
    VALUES (2, 9, 10);

Lorsqu’on sélectionne les données, on trouve la feuille insérée à la bonne place :

id

node_depth

node_left

node_right

1

0

1

20

2

1

2

7

…

5

1

8

11

…

10

2

9

10

NB : Vous pouvez ainsi transformer une feuille en un nœud, tel qu’on vient ici de le faire.

Je pense que vous devinerez comment supprimer une feuille : le topo est à peu près le même que pour l’insertion, sauf que cette fois-ci on procède en sens inverse.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
 * Même si on connaît la borne gauche de l'élément à supprimer, mettons-nous
 * dans un cas où ce n'est justement pas le cas
 */
SELECT node_left
    FROM tuto_ri
    WHERE id = 21;

/*
 * On sait donc que la borne gauche de notre élément est 9 ; on peut donc
 * procéder à la suite
 */

DELETE
    FROM tuto_ri
    WHERE node_left = 9;

UPDATE tuto_ri
    SET node_left = node_left - 2
    WHERE node_left >= 9;

UPDATE tuto_ri
    SET node_right = node_right - 2
    WHERE node_right >= 9;

NB : Pour la suppression, vous n’êtes pas obligés de tout redécaler, mais suivez mon conseil, et faites-le, histoire d’avoir un arbre plus propre et ne pas avoir "trop" de trous. Ceux-ci peuvent devenir problématiques par la suite, spécialement concernant l’organisation et des statisques sur vos nœuds (je pense par exemple au nombre d’enfants pour un nœud précis).

Maintenant, si vous êtes toujours là, on va aborder la même chose… Mais dans le cas général !

Le cas général : l’insertion et la suppression d’un nœud dans un arbre

Je ne pense pas avoir besoin de trop détailler. Vous avez juste besoin de connaître les bornes de l’arbre à insérer, le nombre d’éléments qu’il contient, et ça devrait faire l’affaire si on emploie la même méthode que tout à l’heure. Voici l’arbre1 que l’on va chercher à insérer :

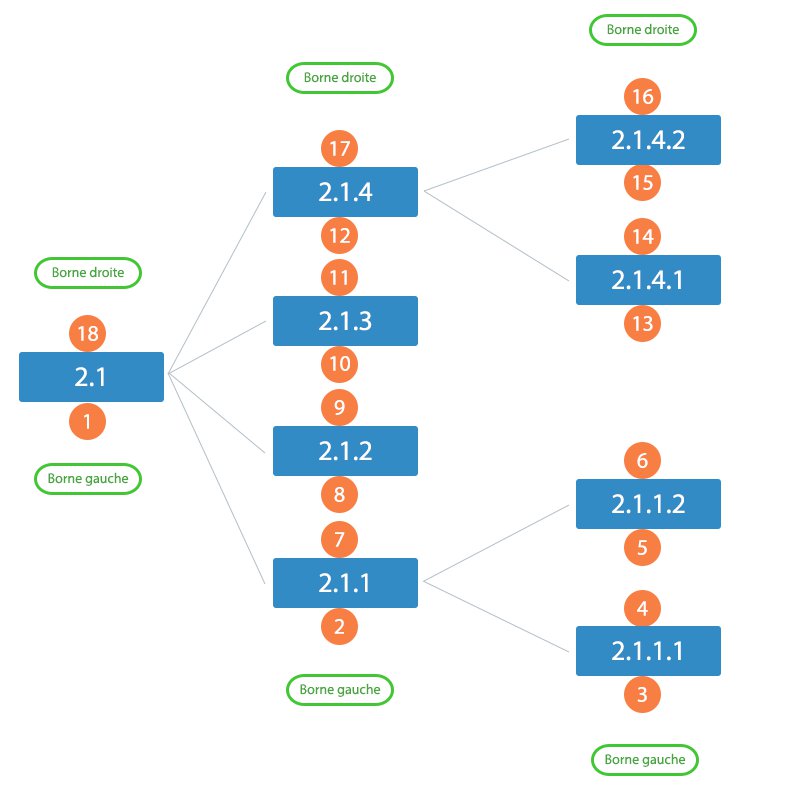
Arbre qu’on va chercher à insérer sur notre arbre de base

On va donc rattacher cet arbre à la feuille ayant l’id n°5, et donc – en considérant notre arbre propre, sans la feuille rajoutée lors de l’exercice précédent – les bornes 8 et 9. Avant de commencer, rendons l’arbre à insérer compatible avec le nœud d’accueil. Pour cela, il nous faut ajouter la borne droite du nœud d’accueil, auquel on retranche un (en effet, la borne gauche du premier élément de l’arbre à insérer commence à 1 et pas 0 !). Soit ici$9 - 1 = 8$.

Occupons-nous maintenant de provoquer un trou dans l’arbre d’accueil. Souvenez-vous du calcul du nombre d’enfants que nous avions abordé dans la partie théorique :

$$ \begin{array}{lcl}\text{borne droite} - \text{borne gauche} & = & 18 - 1 \\\ & = & 17 \\\ & = & 16 + 1 \\\ & = & \boxed{8} \times 2 + 1 \end{array}$$

Si on compte l’élément racine, ça nous fait donc : $8 + 1 = \bf{9}$ éléments) ; il faudra donc ajouter 18 aux bornes gauche et droite des éléments ayant une borne supérieure ou égale à 9. Vous pouvez maintenant faire le rapprochement avec l’ajout d’une feuille : nous ajoutions 2 aux bornes à modifier, car il y avait un élément à insérer.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
SELECT node_right, node_depth
    FROM tuto_ri
    WHERE id = 5;

/*
 * node_right vaut donc 9, et node_depth 1
 */

UPDATE tuto_ri
    SET node_right = node_right + 18
    WHERE node_right >= 9;

UPDATE tuto_ri
    SET node_left = node_left + 18
    WHERE node_left >= 9;

INSERT INTO tuto_ri (node_depth, node_left, node_right)
        VALUES
        (2, 9, 26),
        (3, 10, 15),
        (3, 16, 17),
        (3, 18, 19),
        (3, 20, 25),
        (4, 11, 12),
        (4, 13, 14),
        (4, 21, 22),
        (4, 23, 24);

id

node_depth

node_left

node_right

1

0

1

38

2

1

2

7

…

5

1

8

27

…

10

2

9

26

11

3

10

15

12

3

16

17

13

3

18

19

14

3

20

25

15

4

11

12

16

4

13

14

17

4

21

22

18

4

23

24

Et voici la suppression (vous pouviez la deviner, c’est à peu près la même chose que l’insertion), sauf qu’il faut cette fois-ci récupérer les deux bornes du nœud racine à enlever :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*
 * Même si on connaît la borne gauche et la borne droite de l'élément à
 * supprimer, mettons-nous dans un cas où ce n'est justement pas le cas
 */
SELECT node_left, node_right
    FROM tuto_ri
    WHERE id = 10;

/*
 * On sait donc que la borne gauche de notre élément est donc de 9, et sa borne
 * droite est 26
 */

/* Même si on le connait, récupérons le nombre d'éléments à supprimer */
SELECT COUNT(*)
    FROM tuto_ri
    WHERE node_left >= 9
        AND node_right <= 26

DELETE
    FROM tuto_ri
    WHERE node_left >= 9
        AND node_right <= 26;

UPDATE tuto_ri
    SET node_left = node_left - 18
    WHERE node_left > 9;

UPDATE tuto_ri
    SET node_right = node_right - 18
    WHERE node_right > 26;

C’était tout simplement un mélange entre l’application de la suppression d’une feuille et l’insertion d’un arbre. Comme pour la suppression d’une feuille, les mises à niveau des bornes de l’arbre dans lequel on a supprimé notre nœud ne sont pas obligatoires, mais restent un plus non négligeable pour avoir un arbre propre, et évitera surtout de fausser les statistiques des nœuds. Comme pour l’insertion, pour connaître le nombre à soustraire aux deux bornes, il "suffisait" de connaître le nombre d’éléments à supprimer et de le doubler.

Maintenant qu’on a vu comment insérer et supprimer un nœud d’un arbre, nous allons voir un autre point très intéressant dans la manipulation des arbres : le déplacement de nœuds, qui est en fait une sorte de combinaison de ces deux derniers exercices.

Déplacement d’un nœud

Comme je vous le disais, le déplacement d’un nœud se résume basiquement à deux actions : la "suppression" d’un nœud, et sa "réinsertion".

Mais comme un bon exemple vaut mieux qu’un long discours, tâchons par exemple de déplacer le nœud n°7, et mettons-le à l’extrémité du nœud n°2. J’ai volontairement omis les bornes de ces deux nœuds, pour nous mettre dans un cas où nous ne les connaissons pas. Profitons-en pour également connaître le nombre d’enfants que nous déplaçons.

1
2
3
SELECT node_left, node_right
    FROM tuto_ri
    WHERE id = 7;
id node_left node_right
7 12 17 
1
2
3
4
SELECT COUNT(*)
    FROM tuto_ri
    WHERE node_left >= 12
        AND node_right <= 17;
COUNT(*)
3

Je parlais de suppression, et maintenant qu’on a toutes les informations à notre disposition, on va donc pouvoir supprimer le nœud que nous souhaitons déplacer… Attention, notez bien l’italique sur l’emploi du mot supprimer ! En effet, nous n’allons pas le supprimer de la base de donnée, nous allons juste nous contenter de le cacher dans notre arbre. On appelle ça une zone temporaire.

Pour déplacer un arbre en zone temporaire, il existe deux façons ; soit on met les bornes de notre arbre en négatif, soit en un nombre faramineusement grand. Par préférence, je préfère nettement la première solution ; il est en effet difficile de prévoir la taille de notre arbre, ou de celui de destination. Alors que si nous nous contentons de mettre le nœud déplacé en zone négative, notre arbre peut alors continuer de grossir sans poser trop de problèmes.

Pour cela, il suffit de retrancher la borne droite du nœud à déplacer à toutes ses bornes (gauche comme droite) ;

1
2
3
UPDATE tuto_ri
    SET node_left = node_left - 17, node_right = node_right - 17
    WHERE node_left >= 12 AND node_right <= 17;

Mais maintenant qu’on a "supprimé" notre nœud, et comme nous l’avons vu dans le point précédent, il nous faut alors reboucher le trou ;

1
2
3
4
5
6
7
UPDATE tuto_ri
    SET node_left = node_left - 3 * 2
    WHERE node_left > 12;

UPDATE tuto_ri
    SET node_right = node_right - 3 * 2
    WHERE node_right > 17;

Maintenant que notre nœud est en zone temporaire, il nous faut dès à présent ouvrir un trou où nous le souhaitons. Comme tout à l’heure, sélectionnons alors les bornes du nouveau parent d’accueil (le noeud n°2). Nous aurions pu les connaître lors de la sélection du noeud de départ, mais dans le cas d’un déplacement sur la droite, celles-ci vont changer une fois le rebouchage du trou effectué ! Ce n’est pas notre cas (nous nous déplaçons vers la gauche), mais il est bonne pratique de faire un cas général.

1
2
3
SELECT node_left, node_right
    FROM tuto_ri
    WHERE id = 7;
id node_left node_right
2 2 7

Nous déplacerons donc notre noeud temporaire à l’extrémité du nœud ayant pour bornes (2, 7). Il s’agit du cas que nous avons déjà vu dans la sous-partie précédente ; nous nous occuperons de voir l’autre cas par la suite.

1
2
3
4
5
6
7
UPDATE tuto_ri
    SET node_right = node_right + 3 * 2
    WHERE node_right >= 7

UPDATE tuto_ri
    SET node_left = node_left + 3 * 2
    WHERE node_left >= 7;

Le trou est ouvert ; il ne nous reste plus qu’a réinsérer notre nœud à l’endroit qui convient. Pour cela, plutôt que de faire comme nous avions fait précédemment (soit une bête insertion), il faut juste manipuler les bornes du nœud à déplacer, en leur ajoutant l’ancienne valeur de la borne droite du nouveau parent, le nombre d’éléments dans le nœud à déplacer, et à multiplier le tout par deux pour avoir une différence de bornes consistante.

1
2
3
4
5
6
7
UPDATE tuto_ri
    SET node_right = node_right + 7 + 3 * 2
    WHERE node_right <= 0;

UPDATE tuto_ri
    SET node_left = node_left + 7 + 3 * 2
    WHERE node_left <= 0;

Félicitations, vous avez réussi à déplacer le nœud n°7 dans le nœud n°2.

Au fil de cette explication, Je vous ai parlé de cas un peu spéciaux, qui sont en fait vrai pour l’insertion comme pour le déplacement de nœud ; on a en effet abordé que le cas où nous souhaitions juste insérer notre nœud en tant quedernier enfant du nœud d’accueil. Et maintenant que nous avons vu le déplacement en détail, nous pouvons ainsi voir que les cas suivants existent :

  • Nous souhaitons insérer le nœud avant les autres enfants du nœud d’accueil
  • Nous souhaitons insérer le nœud après un enfant bien particulier du nœud d’accueil
  • Nous souhaitons insérer le nœud après le dernier enfant du nœud d’accueil (s’il en a)

Nous avons déjà traité le troisième cas ; attardons-nous sur les deux premiers cas. En fait, ils ne sont pas si compliqués que ça ; il y a juste quelques paramètres qui changent. Même si la mise en "zone temporaire" et le rebouchage qui suit ne change pas, observons quand même le moment où nous créons un trou et le moment où on insère effectivement notre nœud dans le nœud d’accueil.

Dans le premier cas (nous souhaitons alors insérer notre nœud avant ses frères), plutôt que de se baser sur la borne droite du parent, basons-nous plutôt sur sa borne gauche. Nos requêtes deviennent donc les suivantes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
UPDATE tuto_ri
    SET node_right = node_right + 3 * 2
    WHERE node_right > 2;

UPDATE tuto_ri
    SET node_left = node_left + 3 * 2
    WHERE node_left > 2;

UPDATE tuto_ri
    SET node_right = node_right + 2 + 3 * 2
    WHERE node_right <= 0;

UPDATE tuto_ri
    SET node_left = node_left + 2 + 3 * 2
    WHERE node_left <= 0;

Pour le second cas (nous souhaitons alors insérer notre nœud après un de ses frères), plutôt que de se baser sur la borne droite du parent, nous allons alors nous focaliser sur la borne droite du frère. Mettons que nous souhaitons déplacer le nœud n°7 après le nœud n°3. Une sélection des bornes de ce nœud nous indique alors que ses bornes ont pour valeur le tuple (3, 4).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
UPDATE tuto_ri
    SET node_right = node_right + 3 * 2
    WHERE node_right > 4;

UPDATE tuto_ri
    SET node_left = node_left + 3 * 2
    WHERE node_left > 4;

UPDATE tuto_ri
    SET node_right = node_right + 4 + 3 * 2
    WHERE node_right <= 0;

UPDATE tuto_ri
    SET node_left = node_left + 4 + 3 * 2
    WHERE node_left <= 0;

Félicitations, vous avez maintenant vu comment déplacer et insérer un nœud à n’importe quel endroit de votre arbre !

  1. Réalisé par Alex-D ↩

Vous avez maintenant découvert comment représenter un arbre efficace en SQL, bien que ce ne soit toutefois pas la panacée non plus ; ça peut en effet être gourmand si vous avez une très grosse hiérarchie (ça se verra lors de la numérotation des bornes, les entiers SQL possédant une limite, certes vaste).

Si vous souhaitez creuser un peu plus cette notion, je vous invite à consulter le tutoriel de Frédéric Brouard1 sur ce sujet, et d’ailleurs l’ensemble de ses cours sur le SQL2 qui sont d’ailleurs plutôt bien écrits, si le cœur vous en dit !

  1. http://sqlpro.developpez.com/cours/arborescence ↩

  2. http://sqlpro.developpez.com ↩

12 commentaires

Bonjour !

Je me permets de donner quelques remarques ou suggestions linguistiques concernant cet article. Ce ne sont que des détails, mais je ne me verrais pas critiquer le fond, je ne connaissais rien à la représentation intervallaire avant cet article. Il tombe néanmoins plutôt bien vu que je souhaite me remettre au SQL. Je jetterai un coup d'œil aux cours de Frédéric Brouard ces prochains jours. Merci en tout cas pour ce tutoriel, il est très clair même pour un néophyte comme moi.

  • Chaque forum peut posseder : posséder
  • méthode également connue sous le terme peu barbare de représentation
  • Mais, ceci peut très vite devenir lourd : mais cela (sans virgule et avec cela plutôt que ceci)
  • schmilblik : schmilblick
  • Vérifions le : vérifions-le
  • pour pouvoir pratiquer, dans les deux parties : pas de virgule
  • Et qu'à moins d'avoir
  • devient vite impraticable : j'ajouterais un cela avant pour alléger la proposition.
  • versus étant un mot latin, il se met en italique.
  • consommateur de ressource : de ressources plutôt ?
  • opérations <del>chirurgicales</del> : à formater
  • d'éléments, … : la forme « d'éléments… » est à privilégier. (Plusieurs occurrences.)
  • minis-TP : mini-TP (mini étant un préfixe, il est invariable)
  • se mettre en jambe : jambes
  • on a vu comment récupérer tous les parents (et leur caractéristiques) d'un nœud : on a vu comment récupérer tous les parents d’un nœud (et leurs caractéristiques)
  • Ce qui change ici : supprimer le ici, déjà présent dans la phrase précédente.
  • mais, tâchez juste : la virgule n'est pas pertinente.
  • rappeler d'un des points : rappeler l'un des points
  • nous montrons qu'en fait, notre arbre est loin : j'enlèverais la virgule. Ne faudrait-il pas également mettre la proposition au futur ?
  • seule la sélection de la borne droite
  • une borne gauche et une borne droite supérieures
  • sauf que cette fois-ci, on procède en sens inverse : pas de virgule
  • mettons nous : mettons-nous
  • re-décaler : redécaler
  • Ceux-ci peuvent devenir problématiques
  • spécialement au niveau de l'organisation : spécialement concernant l’organisation (l’utilisation d’au niveau de avec ce sens est un anglicisme)
  • ça devrait faire l'affaire, si on emploie la même méthode : pas de virgule
  • On va donc rattacher cet arbre à la feuille ayant l'id n°5, ayant donc : répétition du ayant un peu gênante
  • mettons nous : mettons-nous
  • il "suffisait" de connaître le nombre d'éléments à supprimer, et à le doubler : à supprimer (sans virgule) et de le doubler
  • tachons par exemple de déplacer : tâchons
  • mettons le : mettons-le
  • l'emploi du mot supprimer : je mettrais de l'italique à supprimer.
  • Autant la mise en "zone temporaire" : problème de syntaxe, ce autant ne se rapporte pas à un autre autant.
  • basons nous : basons-nous
  • nous alors nous focaliser : nous allons ?
  • ça se verra au niveau de la numérotation : le au niveau de me dérange encore, mais je ne vois pas trop comment le remplacer.
  • ses cours sur le SQL qui sont d'ailleurs plutôt bien écrits

Les « NB : » sont parfois suivis d'une minuscule et parfois d'une majuscule, il faudrait peut-être être cohérent sur l'ensemble de l'article. Les deux-points étant normalement suivis d'une minuscule, cette forme aurait ma préférence.

Un petit point typographique me dérange sur cet article, mais c'est un détail de puriste. C’est d'ailleurs peut-être comme les guillemets à corriger directement par le parsage. J’explique mon problème : en réalité, l’abréviation de numéro n’est autre qu’un n avec un o en exposant. En bonne typographie, l'on devrait donc écrire no 5 et non n°5.

+4 -0

Hello,

J'ai pas encore pris le temps de tout lire en détail mais j'ai bookmarké la page et je compte bien tester tout ça.

Par contre je me pose la question des performances : quel est le coût de la sélection d'un arbre entier ? Typiquement, lister toutes les catégories d'un blog (style WordPress) avec la hiérarchie complète, ou plus simplement les enfants d'une catégorie.

Je sens que je vais tester ça et voir ce qu'il est possible de faire à partir de là… :)

+1 -0

Bah justement en fait : à la lecture, il n'y a pas vraiment de problèmes de perf. Mais c'est à l'insertion qu'il faut se poser la question ; si ton arbre est gros (profond), et que tu veux faire régulièrement des insertions, là ça peut éventuellement poser un problème.

Mais pour des catégories WP, ca devrait le faire. :)

edit Par contre, pour la selection entière d'un arbre, faudra que tu fasses le parcours du coté applicatif (PHP, …). Ca dépend après de la taille de ton objet / nombre de colonnes de la table, ça peut être en effet chiant de s'en occuper....

+0 -0

Tiens, y'a quelques années j'avais fait un truc pour faire un menu de saut rapide : https://github.com/Taluu/Talus-Works/blob/master/includes/functions.php#L1052

En gros, ca donnait le résultat qu'on peut voir ici, en bas à droite : http://talus-works.net/topic-227-p1-link-tpl-1-14.html (le petit menu déroulant qui paye pas de mine)

edit oh le bel exemple de fail, je me suis planté de fonction. Mea culpa, j'ai édité le lien. :)

+0 -0

Oh mais je connais Talus TPL ! Je savais bien que ton pseudo me disait quelque chose ! J'avais utilisé ton framework il y a quelques années ^^

Effectivement, je vois bien le principe.

Par contre je vois pas de cas typique où l'arbre serait amené à changer super souvent. Parce que les forums et les catégories de blog, c'est loins d'être hyper variable en général…

Par contre dans ton code je vois bien l'appel à la fonction qui récupère l'arbre, mais pas celle qui le récupère ni celle qui l'affiche…

+0 -0

Celle qui récupère l'arbre est dans une classe helper RI : https://github.com/Taluu/Talus-Works/blob/master/includes/class/ri.php#L296, et celle qui l'utilise est en fait le moteur de TPL (vu par l'appel de block, même si ca date vachement).

Ensuite, https://github.com/Taluu/Talus-Works/blob/master/tpl/files/forums/topic.html#L124.

Enfin, je te déconseille d'utiliser le helper que j'avais fait à l'époque, il est maintenant tout pourri. :D

+0 -0

C'est super utile, cette représentation, en fait ! Pour ma part, ce sont plutôt des use cases où ça deviendrait ennuyeux que j'ai de la peine à trouver…

Petite chose néanmoins : dans la déclaration des données, on parle de node_depth, puis ensuite de node_level, et il y a un joli mélange qui s'ensuit… En fait, dans les gros blocs de code, c'est souvent node_depth, et dans le texte, node_level…

+0 -0

Bonjour,

Je pense qu’il y a une erreur (ou un manque) dans l’algo de déplacement dans le cas où l’on souhaite déplacer un enfant vers un parent dont les bornes sont supérieures (ex : déplacer le nœud n°2, et mettons le à l’extrémité du nœud n°7) Dans ce cas, il faut reprendre les bornes du parent suite au "rebouchage du trou" puisqu’elles auront changé.

Mais sinon, l’article est top! Merci

+1 -0

Hello,

En effet, les bornes du parent à prendre, sont celles au moment ou on fait l’insertion, pas au début de l’opération. Bien vu ! C’est pareil pour un déplacement "sur la gauche", même si de soit les bornes ne changent pas (mais autant faire attention, et prendre la bonne habitude).

Ça me fait penser que j’ai toujours des trucs à corriger (et toujours aussi peu de temps :/)

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte