Introduction au problème du tri

• Une classe d'algorithme non naïfs : diviser pour régner
• Sommaire
• Quelques autres structures de données courantes

Comme on l'a vu, il est facile de rechercher un élément particulier dans un ensemble trié, par exemple un dictionnaire. Mais dans la "vraie vie", ou plutôt dans la vie d'un programmeur, les informations ne sont pas souvent triées. Il se produit même un phénomène assez agaçant et très général : quand on laisse quelque chose changer, ça devient vite le bazar (exemple : votre chambre). Des scientifiques très intelligents ont passé beaucoup de temps à étudier ce principe.

Il y a plusieurs approches pour se protéger de ce danger. La première est de faire très attention, tout le temps, à ce que les choses soient bien rangées. C'est ce que fait par exemple un bibliothécaire : quand on lui rend un livre, il va le poser sur le bon rayon, au bon endroit, et s'il fait bien cela à chaque fois il est facile de trouver le livre qu'on cherche dans une bibliothèque. C'est aussi ce que certains font avec leur chambre, ils passent leur temps à réordonner leurs livres, leurs cahiers, etc. D'autres préfèrent une méthode plus radicale : toutes les semaines, ou tous les mois, ou tous les dix ans, ils font un grand ménage.

Pour l'instant, nous allons nous intéresser au grand ménage : quand on a un ensemble de données dans un ordre quelconque, comment récupérer les mêmes données dans l'ordre ? C'est le problème du tri, et il a de multiples solutions. Curieusement, les méthodes utilisées par l'ordinateur sont parfois très différentes de celles qu'utilisent les humains ; il y a plusieurs raisons, par exemple le fait qu'ils trient souvent beaucoup plus de choses (vous imaginez une chambre avec 5 millions de chaussettes sales ?) mais surtout qu'ils ne font presque jamais d'erreurs et ne s'ennuient jamais.

• Formuler le problème du tri
• Tri par sélection
• Implémentation du tri par sélection
• Le retour du "diviser pour régner" : Tri fusion

Formuler le problème du tri

Pour écrire un algorithme, il faut se mettre bien d'accord sur le problème qu'il résout.

Problème du tri : On possède une collection d'éléments, que l'on sait comparer entre eux. On veut obtenir ces éléments dans l'ordre, c'est-à-dire une collection contenant exactement les mêmes éléments, mais dans laquelle un élément est toujours "plus petit" que tous les éléments suivants.

Vous noterez qu'on n'a pas besoin de préciser quel est le type des éléments : on peut vouloir trier des entiers, des mots ou des chaussettes. On n'a pas non plus précisé de méthode de comparaison particulière : si on veut trier une liste de personnes, on peut la trier par nom, par adresse ou par numéro de téléphone. Même pour des entiers, on peut vouloir les trier par ordre croissant ou par ordre décroissant, c'est-à-dire en les comparant de différentes manières. Le tout est de convenir ce que veut dire "plus petit" pour ce que l'on veut trier (paradoxalement, si l'on veut trier des entiers en ordre décroissant, on dira que 5 est "plus petit" que 3, puisqu'on le veut avant dans la liste triée).

Dans la plupart des cas, on triera des entiers par ordre croissant. C'est le cas le plus simple, et les tris exposés ici seront tous généralisables aux autres situations.

Question de la structure de donnée

Comment sont concrètement stockées nos données ? Nous avons déjà vu deux structures très importantes, les listes et les tableaux. En pratique, vous avez soit une liste soit un tableau sous la main, et vous voulez le trier, vous vous demandez donc "comment trier ma liste" ou "comment trier mon tableau ?".

Il se trouve que les algorithmes pour trier des listes et des tableaux sont assez proches (ils reposent fondamentalement sur les mêmes idées). En général, ce sont les petits détails qui changent. Cependant, il y a tout de même des algorithmes qui utilisent une opération privilégiée d'une des deux structures et ne sont pas adaptés pour l'autre.

Nous allons procéder ainsi : nous commencerons par décrire l'algorithme de tri de manière assez abstraite, en prenant beaucoup de distance, et ensuite nous nous demanderons si l'algorithme est adapté pour chaque structure, et si oui comment l'implémenter. Cela permet à la fois d'avoir une approche généraliste qui fait ressortir les idées essentielles de chaque tri, et de discuter à nouveau des problématiques du choix de la structure de donnée.

Tri par sélection

Le tri par sélection est sans doute le tri le plus simple à imaginer.

On a une suite d'éléments dans le désordre, que l'on va appeler E (comme "entrée"), et on veut construire une suite de résultats, contenant les mêmes éléments dans l'ordre, que l'on va appeler S (comme "sortie").

Quel sera le premier élément de S ? C'est le plus petit élément de E. Il suffit donc de parcourir E, d'en choisir le plus petit élément, et de le mettre en première position dans S. On peut, au passage, l'enlever de la suite E, pour ne pas risquer de se tromper et de l'ajouter plusieurs fois dans S.

Quel sera le deuxième élément de S ? C'est le deuxième plus petit élément de E. Quand on a une suite quelconque, c'est plus difficile de trouver le deuxième plus petit élément que le premier (mais ce n'est pas très difficile, vous pouvez essayer comme Exercice) ; mais ici, on peut jouer sur le fait qu'on a enlevé le plus petit élément, c'est-à-dire qu'on a à disposition la suite E privée de son plus petit élément, que l'on peut noter E'. Le deuxième plus petit élément de E, c'est clairement le premier plus petit élément de E'. Il suffit donc de trouver le plus petit élément de E', le mettre en deuxième position dans S. On peut continuer ainsi pour obtenir le troisième élément, etc. , jusqu'au dernier élément de S.

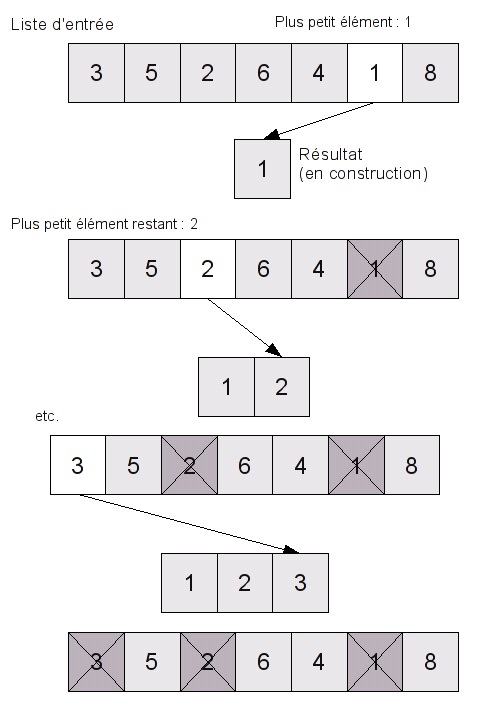
Complexité

Quelle est la complexité du tri par sélection ? C'est assez simple.

• À chaque étape, on trouve le plus petit élément et on le retire ; comme on l'a déjà vu, trouver le plus petit élément est linéaire (O(N), où N est le nombre d'éléments au total) ; retirer un élément est linéaire aussi.
• On répète les étapes jusqu'à avoir retiré tous les éléments. On effectue donc N étapes, si N est le nombre d'éléments à trier. Cela fait donc N fois une opération en O(N), donc du O(N²).

Le tri par sélection est un algorithme en O(N²), ou quadratique.

Implémentation du tri par sélection

Pour une liste

L'algorithme pour les listes est très clair.

On commence par une fonction retire_min, qui à partir d'une liste renvoie son plus petit élément, et la suite privée de cet élément.

Si vous avez lu la première partie, vous savez déjà récupérer le plus petit élément d'une liste, en la parcourant en conservant l'information "quel est le plus petit élément rencontré pour l'instant ?". On procède de la même manière, mais on conserve en plus la liste des éléments non minimums (qui ne sont pas des plus petits éléments) déjà rencontrés : quand on trouve un élément plus petit que le minimum courant, on rajoute le minimum courant dans la liste des "non minimums" avant de passer à l'élément suivant, et à la fin la liste des "non minimum" contient bien tous les éléments, sauf le plus petit.

Une implémentation en caml :

1
2
3
4
5
6

let rec retire_min min_actuel non_minimums = function
| [] -> min_actuel, non_minimums
| tete::queue ->
    (* on met le plus petit (min) comme minimum_actuel,
       et on rajoute le plus grand (max) dans les non-minimums *)
    retire_min (min min_actuel tete) (max min_actuel tete :: non_minimums) queue

Une implémentation en C :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

List *retire_min(List *liste, List *non_mins, int min_actuel)
{
    if (NULL == liste)
        return cons(min_actuel, non_mins);
    else {
        int min = (liste->val < min_actuel ? liste->val : min_actuel);
        int non_min = (liste->val > min_actuel ? liste->val : min_actuel);
        return retire_min(liste->next, cons(non_min, non_mins), min);
    }
}

Remarque : avec cette méthode, l'ordre des éléments dans la "liste des non minimums" n'est pas le même que celui de la liste de départ : si un élément du début de la liste reste le plus petit pendant longtemps, puis est finalement ajouté à la liste non_minimums, il sera loin de sa position de départ (faites dans votre tête un essai sur [1;3;4;5;0] par exemple ; à la fin la liste non_minimums est [3;4;5;1] : le 1 a été déplacé). Mais ce n'est pas grave, parce qu'on va utiliser cette fonction sur la liste d'entrée, qui est en désordre : on va la trier ensuite, donc ce n'est pas un problème si on bouleverse un peu l'ordre des éléments en attendant.

Ensuite, il est très facile de décrire l'algorithme de tri par sélection :

• si la liste E est vide, on renvoie la liste vide
• sinon, on récupère P le premier élément de E, et E' la liste privée de P, on trie E' et on ajoute P devant

1
2
3
4
5

let rec tri_selection = function
| [] -> []
| tete::queue ->
    let plus_petit, reste =  retire_min tete [] queue in
    plus_petit :: tri_selection reste

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

List *tri_selection(List *liste)
{
    if (NULL == liste)
        return NULL;
    else {
        List *selection, *resultat;
        selection = retire_min(liste->next, NULL, liste->val);
        resultat = cons(selection->val, tri_selection(selection->next));
        free_list(selection); /* on libère la liste intermédiaire */
        return resultat;
    }
}

Remarque : on pourrait modifier l'implémentation C de retire_min pour modifier la liste qu'on lui donne au lieu d'en allouer une nouvelle qu'il faut libérer ensuite. Comme ça ne changerait rien à la complexité de l'algorithme (on doit parcourir la liste dans tous les cas, pour trouver le minimum), j'ai choisi de privilégier la simplicité.

De manière générale, les codes que je mets dans ce tutoriel n'ont pas pour but d'être les plus rapides possibles, mais d'être les plus clairs possible (en ayant la bonne complexité). Il y a de nombreuses autres façons d'écrire le même algorithme, certaines étant plus performantes ou moins lisibles. Si vous avez un code plus efficace mais plus compliqué pour le même algorithme, vous pouvez le poster en commentaire, mais je ne changerai l'implémentation du tutoriel que si vous m'en proposez une plus simple ou aussi simple.

Pour un tableau

Quand on trie une liste, on renvoie une nouvelle liste, sans modifier la liste de départ. Pour trier un tableau, on procède souvent (quand l'algorithme s'y prête) différemment : au lieu d'écrire les éléments dans l'ordre dans un nouveau tableau, on modifie le tableau d'entrée en réordonnant les éléments à l'intérieur.

Cette approche a un avantage et un inconvénient. L'avantage c'est qu'il n'y a pas besoin de créer un deuxième tableau, ce qui utilise donc moins de mémoire. On dit que c'est un tri en place (tout est fait sur place, on n'a rien rajouté). L'inconvénient c'est que le tableau de départ est modifié. Si pour une raison ou une autre vous aviez envie de conserver aussi l'ordre initial des éléments (par exemple, si vous vouliez vous souvenir aussi de l'ordre dans lequel les données sont arrivées), il est perdu et vous ne pourrez pas le retrouver, à moins de l'avoir sauvegardé dans un autre tableau avant le tri.

On commence par une fonction qui échange la position de deux éléments dans un tableau.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

<?php
function echange(&$tab, $i, $j)
{
    if ($i != $j) {
        $temporaire = $tab[$i];
        $tab[$i] = $tab[$j];
        $tab[$j] = $temporaire;
    }
}
?>

1
2
3
4
5
6
7
8

void echange(int tab[], int i, int j)
{
    if (i != j) {
        int temp = tab[i];
        tab[i] = tab[j];
        tab[j] = temp;
    }
}

Au lieu de stocker la valeur du minimum, on stocke son indice (sa position dans le tableau) pour pouvoir échanger les cases ensuite.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

<?php
function tri_selection(&$tab)
{
  $taille = count($tab);
  for ($i = 0; $i < $taille - 1; ++$i) {
     $i_min = $i;
     for ($j = $i+1; $j < $taille; ++$j)
        if ($tab[$j] < $tab[$i_min])
          $i_min = $j;
     echange($tab,$i,$i_min);
  }
}
?>

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

void tri_selection(int tab[], int taille)
{
    int i, j;
    for (i = 0; i < taille - 1; ++i) {
        int i_min = i;
        for (j = i + 1; j < taille; ++j)
            if (tab[j] < tab[i_min])
                i_min = j;
        echange(tab, i, i_min);
    }
}

On parcourt le tableau avec un indice i qui va de 0 à la fin du tableau. Pendant le parcours, le tableau est divisé en deux parties : à gauche de i (les indices 0 .. i-1) se trouvent les petits éléments, triés, et à droite les autres éléments dans le désordre. À chaque tour de boucle, on calcule le plus petit élément de la partie non encore triée, et on l'échange avec l'élément placé en i. Ainsi, la partie 0 .. i du tableau est triée, et on peut continuer à partir de i+1 ; à la fin le tableau sera complètement trié. Pour faire le parallèle avec les listes, au lieu de retirer l'élément du tableau, on le met dans une partie du tableau qu'on ne parcours plus ensuite.

Remarque : la boucle sur i s'arrête en fait avant taille-1, et pas avant taille comme d'habitude : quand il ne reste plus qu'un seul élément à trier, il n'y a rien à faire : il est forcément plus grand que tous les éléments précédents, sinon il aurait été choisi comme minimum et échangé, donc il est à la bonne position.

La fonction ne renvoie rien, mais après son exécution le tableau d'entrée est trié.

1
2
3
4
5

<?php // exemple :
$tab = array(1,5,4,3,6);
tri_selection($tab); // modifie le tableau $tab
print_r($tab);
?>

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

#define N 5
int main()
{
    int i, tab[N] = {1,5,4,3,6};
    tri_selection(tab, N); /* modifie le tableau `tab` */
    for (i = 0; i < N; ++i)
        printf("%d ", tab[i]);
    printf("\n");
    return 0;
}

Comparaison

Les deux implémentations de la même idée illustrent bien les différences majeures entre les listes et les tableaux. On utilise dans un cas la possibilité d'ajouter et d'enlever facilement des éléments à une liste, et dans l'autre l'accès arbitraire qui permet de parcourir, comparer et échanger seulement des cases bien précises du tableau.

Tri par insertion

Il existe un tri très proche du tri par sélection, appelé tri par insertion, qui a la même complexité (O(N²)) mais est en pratique plus efficace (car il effectue moins de comparaisons). Vous pouvez vous référer à deux tutoriels le décrivant :

• une version avec des tableaux, à lire en premier, implémentée en C
• une version avec des listes, implémentée en OCaml

Le retour du "diviser pour régner" : Tri fusion

Vous avez maintenant vu le tri par sélection, dont le fonctionnement est assez naturel. Vous vous dites peut-être que finalement, ce tuto est assez inutile, puisqu'il ne fait que parler longuement de chose assez évidentes. Découvrir que pour trier une liste il faut commencer par chercher le plus petit élément, merci, votre petite soeur de deux ans et demi l'aurait deviné (et en plus, elle est mignonne, et elle mange de la purée de potiron, avantages décisifs qui manquent à ce modeste tutoriel).

Nous allons maintenant voir un autre tri, le tri par fusion. Il est surprenant par deux aspects, qui sont très liés :

• il n'est pas du tout naturel au départ ;
• il est beaucoup plus efficace que les tri quadratiques vus jusqu'à présent.

C'est en effet un tri qui a une complexité bien meilleure que les tris par sélection ou insertion. On ne le voit pas sur un petit nombre d'élément, mais sur de très gros volumes c'est décisif. Nous verrons sa complexité en détail après avoir décrit l'algorithme.

Algorithme

L'idée du tri par fusion se décrit en une phrase :

on coupe la liste en deux parts égales, on trie chaque moitié, et on fusionne les deux demi-listes

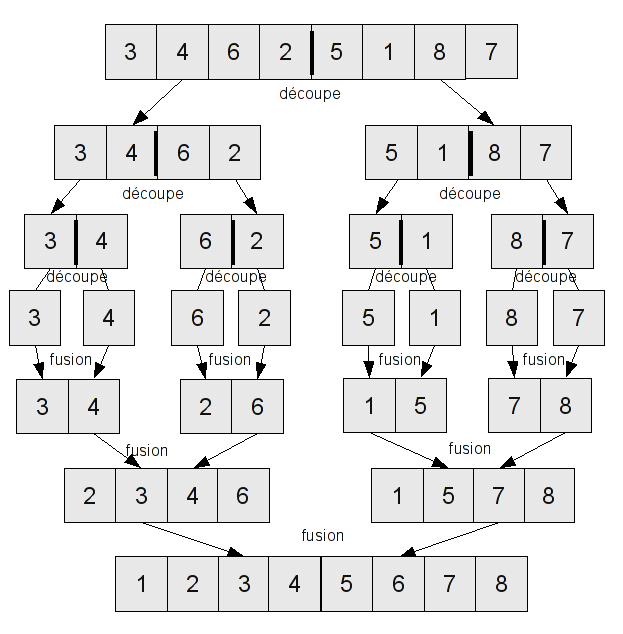
Vous avez bien entendu reconnu une approche de type "diviser pour régner" : on découpe le problème (un tableau => deux demi-tableaux), on traite chaque sous-problème séparément, puis on rassemble les résultats de manière intelligente.

Évidemment, tout le sel de la chose se situe dans la phase de fusion : on a deux demi-listes triées, et on veut obtenir une liste triée. On pourrait se dire qu'il suffit de mettre les deux listes bout à bout, par exemple si on a les deux listes triées [1; 2; 3] et [4; 5; 6], on les colle et pouf [1;2;3;4;5;6]. Malheureusement, ça ne marche pas, prenez par exemple [1; 3; 6] et [2; 4; 5]. Il y a bien quelque chose à faire, et ce quelque chose a intérêt à être efficace : si cette opération cruciale du tri est trop lente, on peut jeter l'ensemble.

L'idée qui permet d'avoir une fusion efficace repose sur le fait que les deux listes sont triées. Il suffit en fait de les parcourir dans l'ordre : on sait que les plus petits éléments des deux listes sont au début, et le plus petit élément de la liste globale est forcément soit le plus petit élément de la première liste, soit le plus petit élément de la deuxième (c'est le plus petit des deux). Une fois qu'on l'a déterminé, on le retire de la demi-liste dans laquelle il se trouve, et on recommence à regarder les éléments du début. Une fois qu'on a épuisé les deux demi-listes, on a bien effectué la fusion.

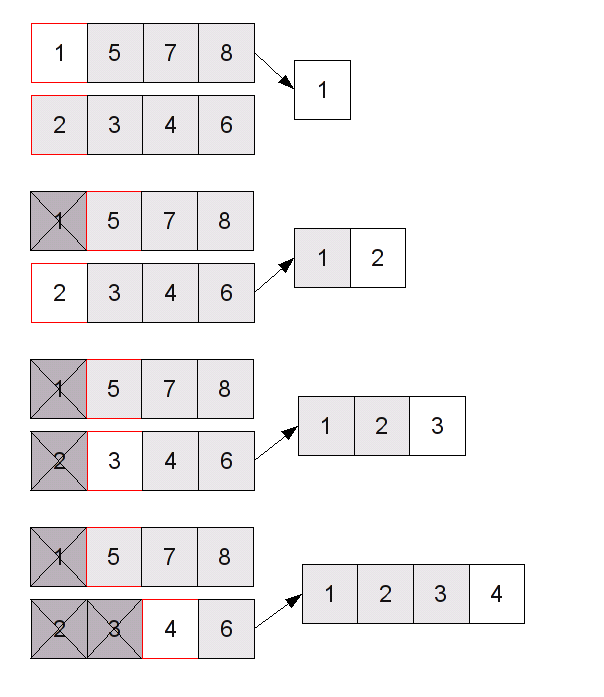
Implémentation avec des listes

Commençons par coder l'opération de fusion d'un couple de listes :

• si l'une des listes est vide, on renvoie l'autre liste ;
• sinon, on compare les têtes de chaque liste, on prend la plus petite et on rappelle la fusion sur la queue de cette liste, et l'autre demi-liste.

En Caml :

1
2
3
4
5
6
7
8

let rec fusion = function
| ([], li) | (li, []) -> li
| tete_a::queue_a, tete_b::queue_b ->
  let bonne_tete, queue, autre_demi_liste =
     if tete_a < tete_b
     then tete_a, queue_a, tete_b::queue_b
     else tete_b, queue_b, tete_a::queue_a in
  bonne_tete :: fusion (queue, autre_demi_liste)

En C :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

List *fusion(List *gauche, List *droite)
{
    if (NULL == gauche)
        return droite;
    if (NULL == droite)
        return gauche;
    if (gauche->val <= droite->val)
        return cons(gauche->val, fusion(gauche->next, droite));
    else
        return cons(droite->val, fusion(gauche, droite->next));                        
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

void print_list(List *liste)
{
    while (NULL != liste) {
        printf("%d ", liste->val);
        liste = liste->next;
    }
    printf("\n");
}

int main()
{
    List *a, *b, *c;
    printf("Éléments de a :\n");
    a = cons(1, NULL);
    print_list(a);

    printf("Éléments de b :\n");
    b = cons(2, cons(3, NULL));
    print_list(b);

    printf("Éléments de c = fusion(a,b) :\n");
    c = fusion(a, b);
    print_list(c);

    printf("Modification du troisième élément c :\n");
    c->next->next->val = 5;
    print_list(c);

    printf("Est-ce que b a été modifiée ?\n");
    print_list(b);

    free_list(a);
    free_list(c);
    return 0;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

List *copy_list(List *liste)
{
    if (NULL == liste)
        return NULL;
    else return cons(liste->val, copy_list(liste->next));
}

List *fusion(List *gauche, List *droite)
{
    if (NULL == gauche)
        return copy_list(droite);
    else if (NULL == droite)
        return copy_list(gauche);
    else if (gauche->val <= droite->val)
        return cons(gauche->val, fusion(gauche->next, droite));
    else
        return cons(droite->val, fusion(gauche, droite->next));                        
}

Il y a une autre opération à implémenter : la découpe d'une liste en deux demi-listes. On parcourt la liste par bloc de deux éléments, en ajoutant le premier dans la demi-liste de gauche, le deuxième dans la demi-liste de droite. S'il reste moins de deux éléments, on met la liste n'importe où (par exemple à gauche) et on met une liste vide de l'autre côté.

En Caml :

1
2
3
4
5

let rec decoupe = function
| ([] | [_]) as liste -> (liste, [])
| gauche::droite::reste ->
    let (reste_gauche, reste_droite) = decoupe reste in
    gauche :: reste_gauche, droite :: reste_droite

En C :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

void decoupe(List *liste, List **gauche, List **droite)
{
    do {
        if (NULL != liste) {
            *gauche = cons(liste->val, *gauche);
            liste = liste->next;
        }
        if (NULL != liste) {
            *droite = cons(liste->val, *droite);
            liste = liste->next;
        }
    } while (NULL != liste);
}

On peut alors écrire facilement le tri (s'il reste moins de deux éléments, la liste est déjà triée donc on la renvoie directement) :

En Caml :

1
2
3
4
5

let rec tri_fusion = function
| ([] | [_]) as liste_triee -> liste_triee
| liste ->
  let demi_gauche, demi_droite = decoupe liste in
  fusion (tri_fusion demi_gauche, tri_fusion demi_droite)

En C :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

List *tri_fusion(List *liste)
{
    if (NULL == liste || NULL == liste->next)
        return copy_list(liste);
    else {
        List *gauche, *droite, *gauche_triee, *droite_triee, *resultat;
        /* au début, gauche et droite sont vides */
        gauche = NULL;
        droite = NULL;
        /* on decoupe la liste en gauche et droite */
        decoupe(liste, &gauche, &droite);
        /* on trie gauche et droite, avant de les libérer */
        gauche_triee = tri_fusion(gauche);
        droite_triee = tri_fusion(droite);
        free_list(gauche);
        free_list(droite);
        /* on fait la fusion des deux listes triées, avant de les libérer */
        resultat = fusion(gauche_triee, droite_triee);
        free_list(gauche_triee);
        free_list(droite_triee);
        /* il ne reste plus qu'à renvoyer le résultat */
        return resultat;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

int main()
{
    List *a, *b, *c;
    a = cons(1, cons(5, cons(4, cons(3, cons(6, NULL)))));
    b = tri_fusion(a);
    print_list(a);
    print_list(b);
    free_list(a);
    free_list(b);
    return 0;
}

Implémentation avec des tableaux

L'implémentation avec des tableaux a des avantages et des inconvénients.

• La phase de découpe est très simple : comme on connaît à l'avance la taille du tableau, il suffit de la diviser par deux et de couper au milieu
• l'opération de fusion est moins naturelle : il faut manipuler les indices

On commence par coder l'opération de fusion. On procède à peu près comme pour les listes, sauf qu'au lieu d'utiliser une procédure récursive, on utilise une boucle pour parcourir les tableaux. On doit conserver trois indices différents :

• la position de lecture dans le premier demi-tableau
• la position de lecture le deuxième demi-tableau
• la position d'écriture dans le tableau résultat

Le dernier indice évolue de façon prévisible : à chaque fois qu'on choisit un élément dans l'une des demi-listes, il augmente de 1. On peut donc l'utiliser comme indice d'une boucle for.

Quand on compare les éléments en tête des deux demi-listes, il faut faire attention à vérifier qu'aucune demi-liste n'est "épuisée" (on a pris tous ses éléments, donc l'indice correspondant est supérieur ou égal à sa taille).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

<?php
function fusion($tab_g, $tab_d)
{
   $taille_g = count($tab_g);
   $taille_d = count($tab_d);
   $res = array(); // tableau résultat
   $i_g = 0; $i_d = 0; // indices de lecture, g->gauche, d->droite
   for ($i = 0; $i_g < $taille_g && $i_d < $taille_d; ++$i)
      if ($tab_g[$i_g] <= $tab_d[$i_d])
         $res[$i] = $tab_g[$i_g++];
      else
         $res[$i] = $tab_d[$i_d++];
   /* on copie le reste du tableau de gauche (s'il reste quelque chose) */
   while ($i_g < $taille_g)
      $res[$i++] = $tab_g[$i_g++];
   /* pareil pour le tableau de droite */
   while ($i_d < $taille_d)
      $res[$i++] = $tab_d[$i_d++];
   return $res;
}
?>

On utilise une fonction copie pour récupérer chaque demi-tableau dans un tableau à part, avant de les trier.

1
2
3
4
5
6
7
8
9

<?php
function copie($tab, $debut, $fin)
{
   $res = array();
   for ($i = $debut; $i <= $fin; ++$i)
      $res[$i - $debut] = $tab[$i];
   return $res;
}
?>

On peut alors écrire le tri entier.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

<?php
function tri_fusion($tab)
{
  $taille = count($tab);
  if ($taille <= 1)
    return $tab;
  else {
    $milieu = (int)($taille / 2);
    $gauche = copie($tab, 0, $milieu-1);
    $droite = copie($tab, $milieu, $taille-1);
    return fusion(tri_fusion($gauche), tri_fusion($droite));
  }
}

// exemple :
$tab = array(1,5,4,3,6);
print_r(tri_fusion($tab));
?>

Remarque : On a utilisé une fonction copie pour copier les deux demi-tableaux en dehors du tableau avant de les trier et de les fusionner. La procédure fusion, elle aussi, crée un nouveau tableau, qu'elle renvoie. On a donc alloué de nouveaux tableaux, ce n'est pas un tri en place. Il est possible de faire mieux : on peut, en manipulant des indices au lieu de tableaux complets, trier les demi-tableau dans le tableau initial, ce qui le modifie mais permet de ne pas allouer de mémoire supplémentaire. Par contre, pour l'étape de fusion il faut tout de même copier des informations, par exemple les deux demi-tableaux triés. Ce n'est toujours pas un tri en place. Il est en fait possible de recopier seulement le demi-tableau de gauche.

Exercice : Écrire (dans le langage de votre choix) un tri fusion sur les tableaux ne recopiant que le demi-tableau de gauche. Pourquoi ça marche ?

Remarque : Il existe des version complètement en place du tri fusion (sans aucune recopie), mais elles sont nettement plus compliquées et souvent moins rapides. Il faut faire un compromis, et la simplicité est souvent le meilleur objectif.

Complexité

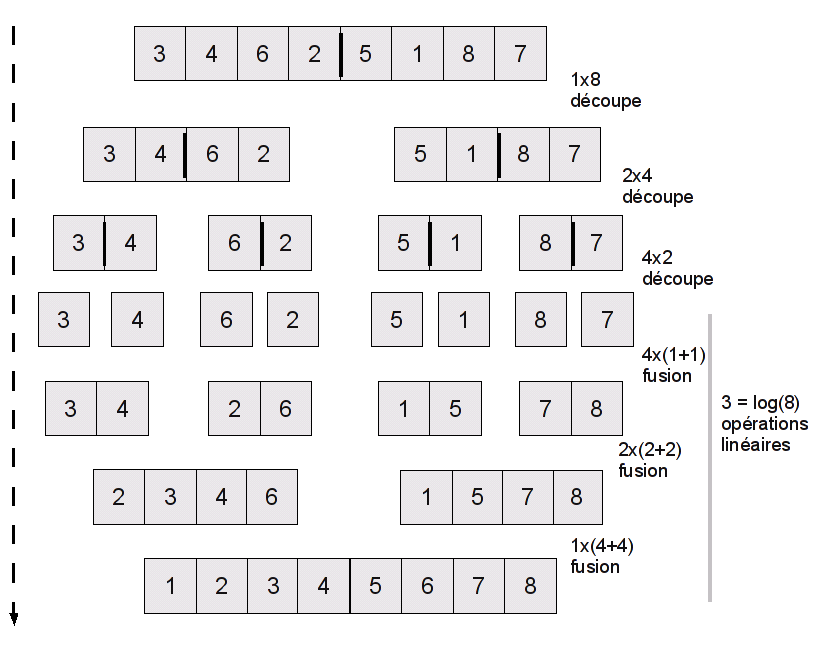
L'étude de la complexité du tri par fusion est assez simple. On commence avec une liste (ou un tableau) de N éléments. On le découpe, ce qui fait deux tableaux de N/2 éléments. On les découpe, ce qui fait 4 tableaux de N/4 éléments. On les découpe, ce qui fait 8 tableaux …

Quand est-ce que la phase de découpage s'arrête ? Quand on est arrivé à des tableaux de taille 1. Et combien de fois faut-il diviser N par 2 pour obtenir 1 ? On l'a déjà vu, c'est la fonction logarithme ! En effet, si on a un tableau de taille 1, on renvoie le tableau en une seule opération (f(0) = 1), et si on double la taille du tableau il faut faire une découpe de plus (f(2*N) = f(N) + 1). C'est bien notre sympathique fonction du chapitre précédent. On a donc log(N) phases de "découpe" successives.

Quel est le travail effectué à chaque étape ? C'est le travail de fusion : après le tri, il faut fusionner les demi-listes. Notre algorithme de fusion est linéaire : on parcours les deux demi-listes une seule fois, donc la fusion de deux tableaux de taille N/2 est en O(N).

Vous allez sûrement me faire remarquer que plus on découpe, plus on a de fusions à faire : au bout de 4 étapes de découpe, on se retrouve avec 16 tableaux à fusionner ! Oui, mais ces tableaux sont petits, ils ont chacun N/16 élément. Au total, on a donc 16 * N/16 = N opérations lors des fusions de ces tableaux : à chaque étape, on a O(N) opérations de fusion.

On a donc log(N) étapes à O(N) opérations chacune. Au total, cela nous fait donc O(N * log(N)) opérations : la complexité du tri fusion est en O(N * log(N)) (parfois noté simplement O(N log N), la multiplication est sous-entendue).

Efficacité en pratique

On est passé, en changeant d'algorithme, d'une complexité de O(N²) à une complexité de O(N * log(N)). C'est bien gentil, mais est-ce si génial que ça ?

La réponse est oui : O(N log(N)) ça va vraiment beaucoup plus vite. Pour vous en convaincre, voici des timings concrets comparant une implémentation du tri par sélection (avec des tableaux) et du tri par fusion (avec des listes), le tout dans le même langage de programmation et sur le même (vieil) ordinateur pour pouvoir comparer :

Les mesures confirment ce que nous avons expliqué jusqu'à présent. On parle bien d'une complexité asymptotique, pour des N grands. Quand N est petit, les deux algorithmes sont à peu près équivalents (pour un petit nombre d'éléments, le tri par insertion va même un peu plus vite que le tri par fusion). La différence se fait sur de grandes valeurs, mais surtout elle caractérise l'évolution des performances quand les demandes changent. Avec une complexité de O(N² ), si on double la taille de l'entrée, le tri par sélection va environ 4 fois plus lentement (c'est assez bien vérifié sur nos exemples). Avec une complexité de O(N * log(N)), cela va seulement un peu plus de 2 fois plus lentement environ (vu les petits temps de calcul, les mesures sont plus sensibles aux variations, donc moins fiables).

En extrapolant ce comportement, on obtient sur de très grandes données un fossé absolument gigantesque. Par exemple, dans ce cas précis, le tri fusion sur 10 millions d'éléments devrait prendre environ une demi heure, alors que pour un tri par sélection il vous faudra… un an et demi.

Ce genre de différences n'est pas un cas rare. On est passé d'un facteur N à un facteur log(N), ce qui est plutôt courant quand on passe d'un code "naïf" (sans réflexion algorithmique) à quelque chose d'un peu mieux pensé. Cela vous donne une idée des gains que peut vous apporter une connaissance de l'algorithmique.

Le passage des tris quadratique aux tri par fusion était impressionnant. Est-ce que dans le prochain chapitre, je vais encore vous décoiffer avec quelque chose d'encore plus magique ? Un tri en O(log(N)) ? Un tri qui renvoie la sortie avant qu'on lui ai donné l'entrée ?

La réponse est non. On dit que le tri fusion est "optimal" parmi les tris par comparaison, c'est à dire qui trient en comparant les élément deux par deux. Si on ne connaît rien des données que l'on trie, on ne peut pas les trier avec une meilleure complexité. Si l'on avait des informations supplémentaires, on pourrait peut-être faire mieux (par exemple si on sait que toutes les valeurs sont égales, bah on ne s'embête pas, on renvoie la liste directement), mais pas dans le cas général. Ce résultat assez étonnant sera montré dans la dernière partie de ce tutoriel (qui n'est pas encore écrite : vous devrez attendre).

Ça ne veut pas dire que le tri par fusion est le meilleur tri qui existe. Il existe d'autres tris (de la même complexité, voire parfois moins bonne dans le pire des cas) qui sont plus rapides en pratique. Mais d'un point de vue algorithmique, vous ne pourrez pas faire beaucoup mieux.

Remarque : c'est le moment de mentionner un petit détail intéressant, qui sort du cadre de l'algorithmique proprement dite. On a déjà expliqué que la mesure de la complexité était de nature asymptotique, c'est à dire qu'elle n'était pertinente que pour de grandes valeurs, à une constante multiplicative près. Il se trouve que pour des petites valeurs (disons jusqu'à 20, 50 ou 100 éléments par exemple), le tri par insertion, bien que quadratique, est très efficace en pratique.

On peut donc donner un petit coup de pouce au tri par fusion de la manière suivante : au lieu de couper la liste en deux jusqu'à qu'elle n'ait plus qu'un seul élément, on la coupe jusqu'à qu'elle ait un petit nombre d'éléments, et ensuite on applique un tri par insertion. Comme on n'a changé l'algorithme que pour les "petites valeurs", le comportement asymptotique est le même et la complexité ne change pas, mais cette variante est un peu plus rapide.

Ce genre de petits détails, qui marchent très bien en pratique, sont là pour nous empêcher d'oublier que l'approche algorithmique n'est pas la réponse à toutes les questions de l'informatique. C'est un outil parmi d'autres, même si son importance est capitale.

• Une classe d'algorithme non naïfs : diviser pour régner
• Sommaire
• Quelques autres structures de données courantes