Pour les fonctions géométriques aussi, les premières choses à définir sont l’ensemble de départ et l’ensemble d’arrivée. La plupart du temps, ces deux ensembles seront les mêmes : si on fait de la géométrie plane, alors notre ensemble de départ sera un plan dans lequel on peut tracer des figures comme des triangles, des polygones ou encore des cercles, et si au contraire on parle de géométrie dans l’espace, on pourra transformer des cubes, des sphères ou des polyèdres.
La géométrie est une discipline aux nombreuses facettes et il est possible d’imaginer des fonctions dans tous les espaces géométriques existants, comme des espaces en dimension 4 ou supérieure ou encore des espaces non euclidiens dans lesquels les distances sont déformées.
Dans ce chapitre, nous limiterons les exemples à la géométrie plane, mais gardez bien à l’esprit que tout cela peut être décliné sous de nombreuses formes.
Représentation des fonctions
Avant de commencer, il faut lever une petite ambiguïté sur l’ensemble de départ et d’arrivée d’une fonction géométrique. En géométrie plane par exemple, il s’agit d’un plan et leurs éléments sont donc les points du plan. Ainsi, une fonction de géométrie plane est une machine à laquelle on donne un point et qui donne un autre point.
Mais alors si l’ensemble de départ ne contient que des points, il n’est pas possible de transformer des figures géométriques ?
Il est vrai qu’habituellement, quand on parle de fonction géométrique, on s’attend plutôt à une machine qui transforme des figures entières. Mais une figure ce n’est rien d’autre qu’un ensemble de points, il est donc facile d’adapter une machine qui transforme des points pour lui faire transformer des figures entières : il suffit de prendre tous les points de la figure et de les transformer en même temps pour former la figure de sortie.
En bref, d’un point de vue parfaitement rigoureux une fonction géométrique ne transforme que des points, mais par abus de langage, on utilise souvent ces fonctions pour transformer des figures entières. Cette distinction peut paraître un peu subtile, et en réalité on l’oublie assez vite quand on passe à la pratique. D’ailleurs nous allons faire cet amalgame dans toute la suite de ce chapitre.
Clem déformée !
Une façon visuelle de représenter une fonction géométrique est de faire un dessin dans notre plan de départ pour pouvoir faire la comparaison entre la position des points avant et après le passage de la fonction.
Voici par exemple comment on peut représenter une telle fonction :

À gauche, on a le dessin de Clem dans le plan de départ, c’est-à-dire avant de transformer les points, puis à droite la même Clem, mais après l’execution de la fonction. On voit que les points se sont déplacés et mélangés. Chaque point du plan de départ se retrouve à un endroit dans le plan d’arrivée.
En réalité, en géométrie, on étudie assez peu ce genre de fonctions qui découpent les figures en petits morceaux comme un puzzle. La plupart des fonctions géométriques intéressantes sont des fonctions dites continues, c’est-à-dire qu’elles déforment et déplacent, mais sans faire de découpage. En voici un exemple :
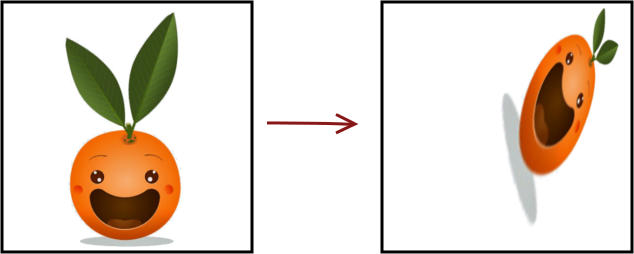
Dans la suite de ce chapitre, nous allons faire un peu de tri en donnant quelques critères qui permettent de classifier ces fonctions.
Tiroirs à fonctions
On peut imaginer une multitude de façons de transformer des figures planes. Nous allons maintenant voir les principales d’entre elles et faire un peu de classement pour mieux s’y retrouver dans cette jungle géométrique.
À quelques adaptations près, toutes les transformations que nous allons voir peuvent également être définies en trois dimensions. Vous pouvez essayer de les imaginer au fur et à mesure.
Les isométries
Les plus simples de toutes les transformations géométriques sont les isométries. Ce sont celles qui conservent les longueurs des figures. Autrement dit, une isométrie se contente de déplacer les figures géométriques sans les déformer.
Le mot isométrie est formé du préfixe grec iso- qui signifie égal et du mot métrie qui désigne la mesure. L’isométrie est donc bien une fonction qui garde les mesures égales. Le préfixe iso- se retrouve par exemple dans l’adjectif isocèle qui qualifie un triangle ayant deux côtés égaux, le mot métrie est également très utilisé, par exemple dans le mot trigonométrie qui désigne l’étude des mesures d’un triangle (aussi appelé trigone).
Faisons un petit tour d’horizon des isométries classiques.
Les translations
Une translation est une transformation qui décale simplement les points d’une certaine distance dans une certaine direction. En voici un exemple :
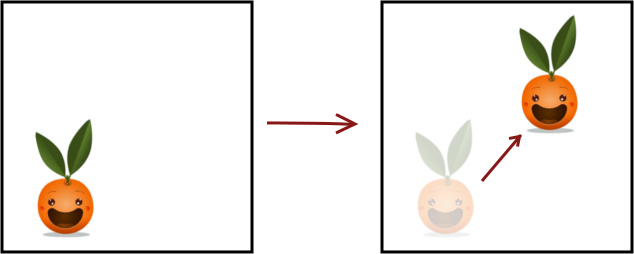
Clem s’est simplement déplacée, sans être ni déformée, ni tournée, ni retournée.
Les rotations
Une rotation est une transformation qui fait tourner les figures d’un certain angle autour d’un point qui se nomme le centre de la rotation. Voici un exemple :
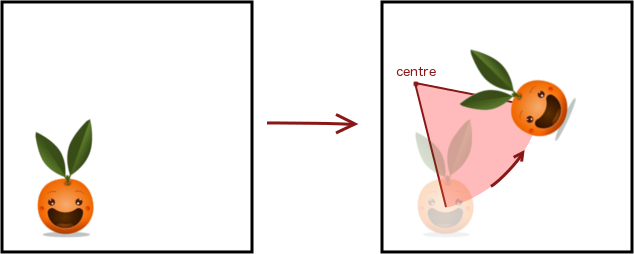
Notez que dans une rotation, le centre est le seul point à ne pas bouger.
Les symétries
Une symétrie est une transformation qui retourne une figure à la façon d’un miroir par rapport à une droite donnée qui se nomme l’axe de symétrie. Voici sa représentation en image :
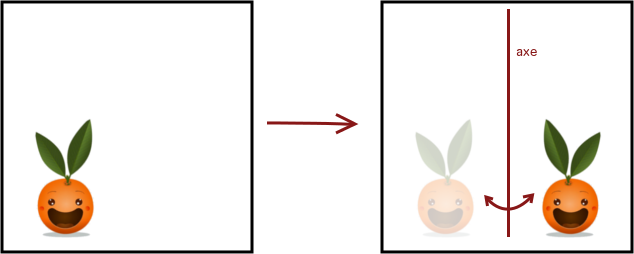
Quand on fait une symétrie, tous les points qui se trouvent sur l’axe ne bougent pas : si on met ces points dans la fonction, elle les rend tels quels sans les avoir modifiés.
Notez que l’exemple ci-dessus s’appelle une symétrie axiale car on fait la symétrie par rapport à une droite (l’axe) dans le plan, mais on peut également faire des symétries par rapport à un point, et même par rapport à un plan quand on fait de la géométrie dans l’espace.
Les trois transformations que nous venons de voir (translations, rotations et symétries), sont les briques de base permettant de reconstituer toutes les autres isométries. Notez que les isométries peuvent être classées en deux catégories :
- Les déplacements qui déplacent la figure sans la retourner. Ce sont celles dans lesquelles il n’y a pas de symétrie, autrement dit, quand on observe l’image de Clem, sa plus petite feuille reste à gauche et la grande à droite. Les translations et les rotations sont des déplacements.
- Les antidéplacements qui retournent la figure. Ce sont celles où une symétrie intervient, éventuellement combinée avec des translations et rotations. Si on regarde l’image de Clem par un antidéplacement, sa petite feuille est passée à droite et sa grande à gauche.
Les transformations affines
Une transformation affine est une fonction géométrique qui conserve les alignements. Autrement dit, si trois points A, B et C sont alignés dans la figure de départ, alors ils le sont toujours à l’arrivée.
Nous en connaissons déjà puisque toutes les isométries sont également des transformations affines. Mais il en existe également qui ne sont pas des isométries, c’est le cas par exemple des homothéties et des transvections que nous allons voir maintenant.
Les homothéties
Une homothétie est une transformation qui agrandit les figures d’un certain rapport à partir d’un point appelé centre de l’homothétie. Voici un exemple avec un rapport égal à à 2 :
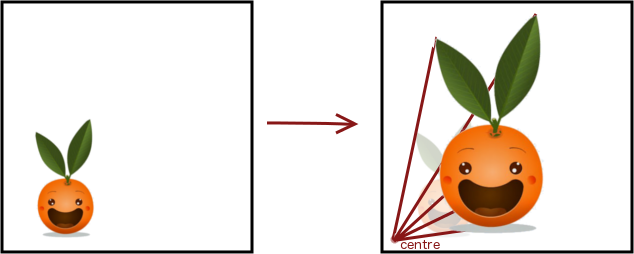
Notez que si le rapport de l’homothétie est plus petit que 1, alors les figures ne sont pas agrandies mais réduites.
Les transvections
Une transvection, aussi appelée cisaillement, est une transformation qui penche les figures dans une certaine direction. Elle est un peu difficile à décrire sans dessin, je vous laisse donc la découvrir avant de la commenter un peu plus :
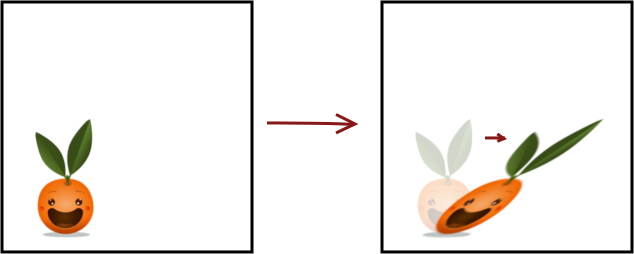
Il s’agit ici d’une transvection horizontale car tous les points sont déplacés en restant sur une même ligne horizontale. Les points situés en bas de Clem ne sont pas déplacés, en revanche, plus on va vers le haut, plus le décalage est important de façon à ce que les alignements soient conservés.
On pourrait construire de la même façon des transvections verticales ou dans n’importe quelle autre direction donnée et avec des décalages plus ou moins importants.
Les transformations conformes
Une transformation conforme est une transformation géométrique qui conserve les angles. Bien entendu, les isométries sont également des applications conformes, mais il y en a bien d’autres.
Ces applications peuvent sembler un peu mystérieuses la première fois qu’on les rencontre car il est assez difficile d’imaginer des transformations des figures qui conservent les angles sans conserver les alignements. En voici un exemple en image :
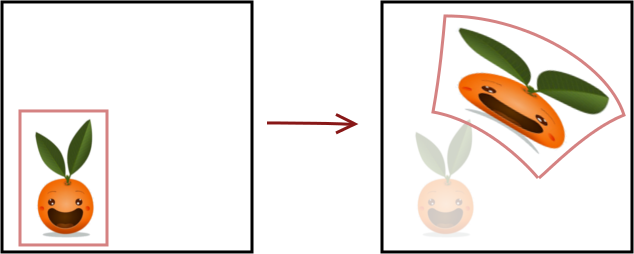
Le rectangle placé autour de Clem permet de constater que les quatre angles sont bien toujours des angles droits malgré la déformation des lignes.
Les similitudes
Les similitudes sont les transformations qui conservent à la fois les angles et les alignements. Ainsi, les similitudes conservent parfaitement les formes des objets, c’est-à-dire que l’image d’une figure sera une figure semblable.
Pour trouver toutes les similitudes, il faut donc prendre les transformations que nous venons de voir et exclure les transformations conformes qui ne conservent pas les alignements, ainsi que les transformations affines qui ne conservent pas les angles (comme les transvections). Une fois ce tri effectué, il ne reste plus que les isométries et les homothéties. Ainsi, une similitude est une combinaison de translations, de rotations, de symétries et d’homothéties.
En voici un exemple :
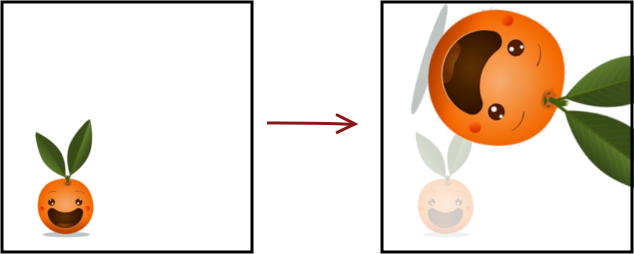
Descartes s'en mêle
Au XVIIe siècle, le mathématicien et philosophe français René Descartes inventa un pont permettant de relier la géométrie à l’étude des nombres. Son idée était la suivante : repérer les points d’un plan par deux nombres que l’on nomme ses coordonnées. Pour cela, il suffit de disposer de deux axes gradués, le premier, horizontal, nommé axe des abscisses et le second, vertical, nommé axe des ordonnées.
Voici par exemple comment sont situés dans le plan les points de coordonnées (3,5) et (-7,-1) :
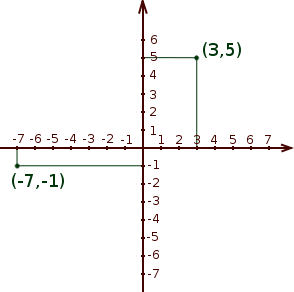
Cette passerelle jetée par Descartes entre les deux domaines est extraordinaire, elle permet de traduire tout ce que l’on fait en géométrie en termes algébriques et inversement. Ainsi, toute fonction géométrique du plan peut être vue comme une fonction numérique à deux variables.
Par exemple, l’homothétie de rapport 2 et dont le centre se trouve à l’intersection des deux axes s’exprime de la façon suivante :
Autrement dit, les coordonnées sont simplement multipliées par 2. La symétrie par rapport à l’axe horizontal s’écrit comme ceci :
La première coordonnée reste inchangée, par contre la deuxième devient son opposé, ce qui correspond bien dans le plan au fait de passer d’un côté à l’autre de l’axe des abscisses.
Les deux exemples ci-dessus sont parmi les plus faciles à exprimer, mais toutes les fonctions géométriques peuvent se traduire de cette façon. Si vous avez envie de faire un peu chauffer vos neurones, essayez d’exprimer en termes algébriques quelques-unes des autres transformations géométriques que nous avons vues dans ce chapitre : translation, transvection, rotation d’un quart de tour, homothétie dont le centre se trouve en un autre point que le centre du repère…
