Haskell est un langage au typage fort et statique. Les types ont souvent une assez grande importance dans un programme : ils permettent d'éviter un certain nombre de bugs, en vérifiant qu'on manipule toujours les données de manière correcte. Mais les types prédéfinis ne suffisent pas toujours à assurer ces propriétés.
Par exemple, que faire si on veut un type similaire à Either mais avec 3 possibilités ? Si on représente les coordonnées d'un point dans l'espace par un triplet de réels, et qu'on utilise la même représentation pour une couleur, comment faire pour ne pas les confondre ? Et quel type utiliser pour représenter un arbre binaire ?
Pour résoudre tous ces problèmes, il faut pouvoir créer de nouveaux types, ce qui est le sujet de la première partie de ce chapitre. La partie suivante s'intéresse aux classes de types : avec quelques exemples, vous verrez comment déclarer un type comme instance d'une classe, et comment créer vos propres classes de types.
Déclarer un type
Il existe trois manières de déclarer un type en Haskell, qui ont toutes une utilité différente.
type : un autre nom pour un type
Avec type, vous pouvez déclarer un nouveau nom pour un type qui existe déjà. Par exemple, vous avez déjà vu que le type String est en fait un autre nom pour le type [Char]. En réalité, le type String est défini de la façon suivante :
1 | type String = [Char] |
Ce genre de définition ne crée pas à proprement parler un nouveau type : les deux types String et [Char] sont interchangeables, String n'est qu'un autre nom pour [Char]. Cependant, ce genre de définition présente un avantage quand on écrit le type d'une variable. Par exemple, si on utilise (Double,Double,Double) comme type pour représenter une couleur, et qu'on crée une liste de couleurs, si on indique le type comme dans l'exemple ci-dessous, son rôle est assez obscur :
1 2 3 4 5 | palette :: [(Double,Double,Double)] palette = [(1,0,0), (0,1,1), (0,1,0)] inverser :: (Double,Double,Double) -> (Double,Double,Double) inverser (r,g,b) = (1-r,1-g,1-b) |
Comparez avec ce code-là, où on a défini un type avec type. Le code est tout de suite plus clair, et comme c'est moins long d'écrire les signatures de chaque valeur, vous pourrez toutes les écrire sans perdre votre temps, ce qui fait que le code est plus sûr et plus compréhensible.
1 2 3 4 5 6 7 | type Couleur = (Double, Double, Double) palette :: [Couleur] palette = [(1,0,0), (0,1,1), (0,1,0)] inverser :: Couleur -> Couleur inverser (r,g,b) = (1-r,1-g,1-b) |
Pour définir en général un nouveau nom pour un type déjà existant, il faut écrire : type NomDuType = UnAutreType (Au,Nom) Super Long
Les noms de types doivent toujours commencer par une majuscule. Par exemple, MonSuperType est un nom valide, pas monSuperType
Utiliser data pour définir des types algébriques
La deuxième manière de déclarer des types utilise data. Cette construction permet de faire beaucoup de choses, comme vous allez le voir dans les paragraphes qui suivent.
Des énumérations
Imaginons que vous êtes en train de coder un logiciel pour un marchand de glace. Ce marchand vend des glaces avec plusieurs goûts différents, et certains coûtent plus cher que d'autres. Il faut donc coder une fonction qui, pour un parfum donné, renvoie le prix d'une boule de glace à ce goût-là. Pour cela, il faut d'abord vous demander comment vous allez représenter un parfum. Une première solution serait d'utiliser des chaînes de caractères; la fonction ressemblerait à ceci :
1 2 3 4 5 6 | type Parfum = String prixParfum :: Parfum -> Double prixParfum "chocolat" = 1.5 prixParfum "vanille" = 1.2 prixParfum "framboise" = 1.4 |
Le problème, c'est qu'il est très facile d'introduire des valeurs invalides, comme "qsd%ù&é" (ou de faire une faute d'orthographe quelque part dans le code). Pour être sûr de ne pas faire d'erreur, il faudrait mettre beaucoup de vérifications dans toutes les fonctions qui utilisent des parfums. Et même dans ce cas, on ne profite pas du système de types : les erreurs ne sont pas détectées à la compilation. On pourrait représenter les parfums avec des entiers, mais on se retrouve avec le même problème. On va donc utiliser data pour faire une énumération :
1 2 3 4 | data Parfum = Chocolat | Vanille | Framboise deriving Show |
Cette fois, on a créé un nouveau type. Cette déclaration veut dire qu'une valeur de type Parfum est soit Fraise, soit Framboise, soit Chocolat. Le deriving Show à la fin de la déclaration fait que ghc génère automatiquement une instance de Show pour notre type, si c'est possible. Cela nous permet notamment de travailler facilement avec dans ghci, c'est donc une bonne idée de l'indiquer.
Maintenant, pour traiter des valeurs de notre nouveau type, on doit utiliser le filtrage de motif. Ici, on définit la fonction prixParfum pour utiliser notre nouveau type :
1 2 3 4 | prixParfum :: Parfum -> Double prixParfum Chocolat = 1.5 prixParfum Vanille = 1.2 prixParfum Framboise = 1.4 |
On peut définir d'autres énumérations avec data, mais un nom ne doit être utilisé qu'une fois. Il est donc impossible de créer une autre énumération qui comprend une valeur comme Chocolat, Vanille ou Framboise. On peut redéfinir les booléens de cette façon :
1 | data Booleen = Vrai | Faux |
Types algébriques
Vous savez maintenant utiliser data pour créer des énumérations. Mais ce n'est qu'un cas particulier de quelque chose de plus général : les types algébriques, qu'on définit avec data. Revenons à notre logiciel pour commander des glaces. Le glacier fait deux types de glace : des glaces à une boule, et des glaces à deux boules. On pourrait utiliser une liste pour représenter ces deux types de glace, mais dans ce cas, on risque d'avoir des commandes pour des glaces à 0 boule ou à 3 boules, alors que le glacier n'en fait pas. On va donc utiliser data pour créer un nouveau type :
1 2 3 | data Glace = UneBoule Parfum | DeuxBoules Parfum Parfum deriving Show |
Si on prononce "|" comme "ou", le sens de cette déclaration devient évident : une glace est soit une glace à une boule ayant un parfum, soit une glace à deux boules ayant deux parfums. Ensuite, on utilise le filtrage de motif pour différencier les deux cas dans nos fonctions :
1 2 | prixGlace (UneBoule a) = 0.10 + prixParfum a prixGlace (DeuxBoules a b) = 0.15 + prixParfum a + prixParfum b |
Ainsi, pour créer un type avec data, on donne une liste de possibilité (les différents constructeurs, UneBoule et DeuxBoules dans le cas de glace), et les attributs qui correspondent à chaque possibilité.
Par exemple, pour un programme de dessin, on pourrait vouloir représenter des formes géométriques : cercle et rectangle. Pour définir un cercle, on a besoin de son centre (un point), et de son rayon; pour définir un rectangle, il faut deux points : la position du sommet en bas à gauche, et celle du sommet en haut à droite. Vous pouvez donc essayer d'écrire le type correspondant, et des fonctions aire et perimetre qui renvoient l'aire et le périmètre d'une forme.
1 2 3 4 5 6 7 8 9 10 11 | type Point = (Float,Float) data Forme = Cercle Point Float | Rectangle Point Point aire :: Forme -> Float aire (Rectangle (a,b) (c,d)) = abs (a-c) * abs (b-d) aire (Cercle _ r) = pi * r^2 perimetre :: Forme -> Float perimetre (Rectangle (a,b) (c,d)) = 2 * ( abs (a-c) + abs (b-d) ) perimetre (Cercle _ r) = 2 * pi * r |
La troisième façon de définir des types en Haskell est d'utiliser newtype. En fait, newtype est un cas particulier de data : il permet seulement de définir des types à un seul constructeur, et ce constructeur ne doit prendre qu'un seul argument. Par exemple, pour éviter de mélanger les points avec autre chose, on pourrait écrire newtype Point = Point (Float, Float) (le Point à gauche du signe = est un nom de type, celui à droite le nom d'un constructeur de type, donc utiliser deux fois le nom Point ne pose pas de problème ici). La seule différence est qu'avec newtype, le compilateur sait qu'une valeur de type Point utilise forcément le constructeur Point, donc peut optimiser le programme pour qu'il fonctionne comme si on utilisait le type (Float,Float) à la place de Point. Cependant, quand le compilateur vérifie les types, les deux types sont différents, ce qui permet de repérer les erreurs où on utilise l'un à la place de l'autre.
Enregistrements
Maintenant, le glacier veut garder un profil de chacun de ses utilisateurs. Pour cela, il veut stocker le nom, le prénom, l'adresse e-mail, la date des première et dernière commandes de ce client, et la somme totale dépensée chez le glacier. On a donc toutes les informations nécessaires pour créer un type, et quelques fonctions utiles :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | data Date = Date Int Int Int -- Une date : jour/mois/année data Client = Client String String String Date Date Float -- Créer un nouveau client qui n'a encore rien commandé nouveauClient :: String -> String -> String -> Client nouveauClient nom prenom mail = Client nom prenom mail (Date 0 0 0) (Date 0 0 0) 0 -- Actualiser les infos d'un client qui vient de passer une commande actualiserClient : Date -> Float -> Client -> Client actualiserClient date somme (Client nom prenom mail premiereCommande _ sommeCommandes) = Client nom prenom mail premiereCommande date (sommeCommandes + somme) -- Donne l'adresse mail d'un client mailClient :: Client -> String mailClient (Client _ _ mail _ _ _) = mail |
Comme vous le voyez, ce type n'est pas facile à manipuler : on ne voit pas nettement le nom des champs, donc on risque d'inverser l'ordre de deux champs de même type, et d'avoir une erreur non trouvée par le système de type, ce n'est pas facile d'accéder à un champ du type, et quand on veut modifier une valeur, on est obligé de copier toutes les autres explicitement, ce qui fait du code vraiment très lourd.
Heureusement, pour ce genre de choses, on peut utiliser les enregistrements. On définit un type d'enregistrement comme ceci :
1 2 3 4 5 6 7 8 | data Client = Client { nom :: String, prenom :: String, mail :: String, premiereCommande :: Date, derniereCommande :: Date, sommeCommandes :: Float } deriving Show |
On peut toujours créer un client en utilisant le constructeur et en donnant la valeur des champs dans l'ordre, mais on peut aussi indiquer le nom des champs. Dans ce cas, l'ordre n'importe pas :
1 2 3 4 5 6 7 8 9 | unClient = Client { nom = "Dupont", prenom = "Hubert", mail = "hubert.dupont@example.com", premiereCommande = Date 1 2 2003, derniereCommande = Date 9 9 2009, sommeCommandes = 13.3 } autreClient = Client "Dupont" "Robert" "rdupont@example.com" (Date 29 2 2003) (Date 1 10 2009) 42 |
On peut aussi utiliser le nom des champs avec le filtrage de motif. Cependant, quand on définit un enregistrement, des fonctions sont automatiquement créées pour accéder à chacun des champs :
1 2 3 | nomPrenom (Client {nom = nom, prenom = prenom}) = nom ++ " " ++ prenom nomPrenom' client = nom client ++ " " ++ prenom client |
Enfin, on dispose d'une syntaxe plus pratique pour modifier seulement quelques champs d'un enregistrement :
1 2 3 4 5 | actualiserClient :: Date -> Float -> Client -> Client actualiserClient date somme client = client { derniereCommande = date, sommeCommandes = sommeCommandes client + somme } |
Types récursifs, types paramétrés
Des paramètres pour les types
Dans cette partie, on va créer un nouveau type qui correspond aux listes à au moins un élément. Ce n'est pas forcément un type utile dans toutes les situations, mais des fois il peut être utile, pour des opérations qui n'ont pas de sens sur des listes vides. Une façon simple de créer un type qui correspond est de prendre une paire constituée d'un élément, et d'une liste d'éléments, ce qui garantit qu'on a au moins un élément. Cependant, en essayant de déclarer un tel type, vous allez avoir un problème : quel est le type de l'élément ? On va commencer par définir notre type pour les entiers, et une ou deux fonctions :
1 2 3 4 5 6 7 | data SomeInt = SomeInt Int [Int] someIntToList :: SomeInt -> [Int] someIntToList (SomeInt x xs) = x:xs addInt :: Int -> SomeInt -> SomeInt addInt i s = SomeInt i (someIntToList s) |
On pourrait alors redéfinir un type à chaque fois qu'on veut un type différent pour les éléments. Mais ça nous oblige aussi à redéfinir les fonctions. On pourrait le faire par copier-coller, mais vous savez déjà que c'est une bonne façon de faire des erreurs bêtes, et de les copier partout dans le programme pour les rendre impossible à corriger, et que ça va à l'encontre du premier principe du programmeur (et de n'importe qui) : faire le moins possible de choses inutiles et inintéressantes. Dans ce cas, les fonctions ne font rien de spécial sur les éléments contenus dans le type SomeInt, on devrait donc pouvoir en faire des fonctions polymorphes. C'est ce qu'on ferait avec des listes, ou avec Maybe. Pour résoudre ce problème, on va utiliser les types paramétrés :
1 2 3 4 5 6 7 | data Some a = Some a [a] someToList :: Some a -> [a] someToList (Some x xs) = x:xs add :: a -> Some a -> Some a add i s = Some i (someToList s) |
En fait, vous aviez déjà utilisé des types paramétrés, comme Maybe ou le type des listes. La seule chose que vous ne saviez pas faire, c'est en définir. Maintenant, vous êtes capables de redéfinir le type Maybe, mais pas encore le type des listes : ce sera le sujet de la suite.
Notez que vous pouvez aussi utiliser des paramètres quand vous déclarez un alias avec type, de la même façon qu'avec data. Il est aussi possible de prendre plusieurs paramètres. Vous pouvez donc définir des types comme :
1 2 3 | -- Ce type représente des listes d'associations : par exemple [("Jean Dupont", 42), ("Jean Bon", 12)] -- pour représenter l'argent dans le compte en banque d'un certain nombre de personnes type Assoc a b = [(a,b)] |
Types récursifs
Rappelez-vous du chapitre sur les suites : elles sont définies par deux constructeurs possibles, [] (la liste vide), et : qui permet d'ajouter un élément en tête d'une liste, et qui prend donc deux arguments, un élément et une liste d'éléments. Ce type est défini en fonction de lui même : c'est un type récursif.
Pour vous montrer comment définir des types récursifs, on va créer un type MyList a, qui correspond en fait au type [a], avec deux constructeurs : Nil et Cons.
1 | data MyList a = Nil | Cons a (MyList a) |
Voilà, définir un type récursif n'est pas vraiment compliqué. Ensuite, on peut l'utiliser comme n'importe quel type normal :
1 | liste = Cons 1 (Cons 2 (Cons 3 Nil)) |
Exemples
Manipuler des arbres
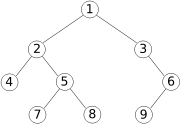Un arbre binaire est une structure de donnée qui peut se représenter sous la forme d'un arbre, dont chaque noeud contient une valeur et deux éléments fils (c'est à dire deux arbres), comme sur la figure ci-contre.
On voit bien qu'une telle structure de données se définit très facilement de manière récursive : à chaque niveau, soit on est arrivé au bout de l'arbre (représenté par le constructeur Feuille), soit on arrive à un embranchement, où l'arbre se sépare en deux branches. À chaque embranchement, on trouve un élément.
1 2 3 | data Arbre a = Branche a (Arbre a) (Arbre a) | Feuille deriving Show |
Par exemple, l'arbre donné comme exemple est représenté de la façon suivante :
1 2 3 4 5 6 7 8 9 10 11 | arbreExemple = Branche 1 (Branche 2 (Branche 4 Feuille Feuille) (Branche 5 (Branche 7 Feuille Feuille) (Branche 8 Feuille Feuille))) (Branche 3 Feuille (Branche 6 (Branche 9 Feuille Feuille) Feuille)) |
On appelle profondeur d'un arbre la distance maximale de la racine à une Feuille. Par exemple, si la racine est une Feuille, la profondeur vaut 0. On peut donc calculer la profondeur d'un arbre à l'aide d'une fonction récursive. On veut aussi des fonctions pour calculer le nombre de branches et le nombre de feuilles d'un arbre. On crée aussi une fonction permettant de calculer la somme des éléments d'un arbre.
1 2 3 4 5 6 7 8 9 10 11 | profondeur Feuille = 0 profondeur (Branche _ gauche droite) = 1 + max (profondeur gauche) (profondeur droite) feuilles Feuille = 1 feuilles (Branche _ gauche droite) = feuilles gauche + feuilles droite branches Feuille = 0 branches (Branche _ gauche droite) = 1 + branches gauche + branches droite somme Feuille = 0 somme (Branche el gauche droite) = el + somme gauche + somme droite |
Comme vous pouvez le constater, ces fonctions se ressemblent beaucoup : on donne une valeur fixée pour les Feuilles, et pour chaque Branche, on combine les résultats obtenus avec la fonction sur les deux sous-arbres. On aimerait bien créer une fonction d'ordre supérieur pour factoriser ce code. Si vous suivez vraiment attentivement, vous devriez avoir une impression de déjà vu : dans le chapitre sur les listes, c'est à partir d'un procédé de récursivité utilisé par un certain nombre de fonctions qu'on a montré l'utilité de la fonction foldr sur les listes. Et en effet, la fonction d'ordre supérieur foldArbre qu'on va créer suit le même principe :
1 2 3 4 5 6 7 8 9 | foldArbre f n Feuille = n foldArbre f n (Branche e d g) = f e (foldArbre f n d) (foldArbre f n g) profondeur' = foldArbre (\ _ d g -> 1 + max d g) 0 feuilles' = foldArbre (\ _ d g -> d + g) 1 branches' = foldArbre (\ _ d g -> 1 + d + g) 0 somme' = foldArbre (\ e d g -> e + d + g) 0 retourner = foldArbre (\ e d g -> Branche e g d) Feuille |
Pour vous convaincre de la similarité entre foldr et foldArbre, comparez ces deux schémas :
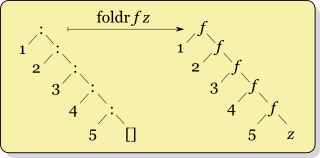
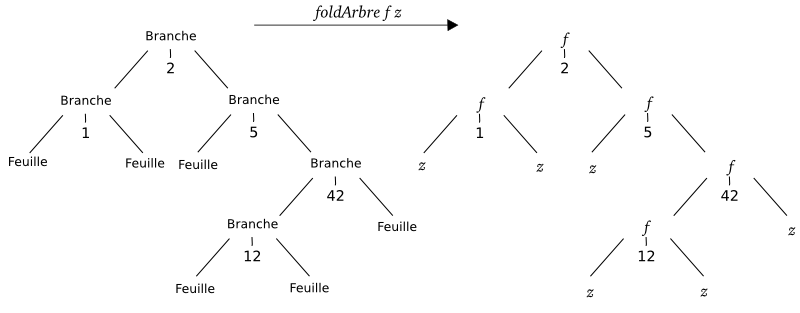
Dans les deux schémas, fold remplace tous les constructeurs Branche par un appel à la fonction f, et tous les constructeurs Branche (qui ne prennent pas d'argument) par la valeur z. On peut définir de manière similaire une opération fold sur tous les types récursifs.
Arbres binaires de recherche
Les arbres binaires servent de base à un certain nombre de structures de données. Une structure simple et pourtant intéressante est l'arbre binaire de recherche (ou ABR). C'est un arbre binaire qui doit respecter une propriété particulière : pour chaque noeud de l'arbre, tous les éléments dans la branche gauche de l'arbre doivent être inférieurs à l'élément placé dans le noeud, et tous ceux situés à droite doivent être supérieurs. Par exemple, l'arbre ci-contre est un arbre binaire de recherche, mais celui donné comme exemple d'arbre n'en est pas un.
On peut déjà créer une fonction qui teste si un arbre est un ABR ou pas, et la tester dans ghci :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | -- teste si une propriété p est respectée par tous les éléments d'un arbre allArbre _ Feuille = True allArbre p (Branche e g d) = p e && allArbre p g && allArbre p d abrValide Feuille = True abrValide (Branche e g d) = allArbre (< e) g && allArbre (> e) d && abrValide g && abrValide d abr = Branche 10 (Branche 5 Feuille (Branche 8 (Branche 7 Feuille Feuille) (Branche 9 Feuille Feuille))) (Branche 20 (Branche 15 (Branche 12 Feuille Feuille) (Branche 17 Feuille Feuille)) (Branche 25 Feuille Feuille)) invalide = Branche 10 Feuille (Branche 3 Feuille Feuille) |
1 2 3 4 | Prelude> abrValide abr True Prelude> abrValide invalide False |
Si un arbre binaire s'appelle un arbre binaire de recherche, c'est bien parce qu'il est facile de rechercher des éléments dedans. Imaginons qu'on veuille vérifier si un élément est dans l'arbre. On se trouve donc à une Branche. Soit l'élément se trouve à cette branche, soit il se trouve à gauche, soit il se trouve à droite. On doit donc parcourir tout l'arbre pour savoir si un élément se trouve dans l'arbre avec cette méthode, ce n'est donc pas plus efficace que de chercher dans une simple liste. Cependant, on n'a pas pris en compte la propriété de l'arbre binaire de recherche, donc notre algorithme marche même sur un arbre binaire normal. Dans le cas des arbres binaires de recherche, on sait que les éléments sont ordonnés. Donc, quand on se trouve à une Branche, on peut décider de quel côté aller chercher l'élément. On a donc qui un algorithme, qui au lieu d'explorer les deux possibilités à chaque branche n'en choisit qu'une seule : il est donc beaucoup plus performant.
1 2 3 4 | rechercher _ Feuille = False rechercher e (Branche f g d) | e == f = True | e < f = rechercher e g | e > f = rechercher e d |
On teste ce code dans ghci pour voir s'il marche comme prévu :
1 2 3 4 5 6 | *Main> rechercher 15 abr True *Main> rechercher 10 abr True *Main> rechercher 100 abr False |
Et voilà, il a l'air de marcher correctement. Maintenant, on a besoin d'autres opérations pour manipuler les ABR, par exemple ajouter et supprimer des éléments. Pour ajouter un élément, on fait comme pour rechercher un élément, sauf qu'on reconstruit un nouvel arbre avec les données, et qu'on ajoute l'élément dès qu'on rencontre une feuille :
1 2 3 4 | inserer e Feuille = Branche e Feuille Feuille inserer e (Branche f g d) | e == f = Branche f g d | e < f = Branche f (inserer e g) d | e > f = Branche f g (inserer e d) |
Ce code ne modifie pas l'arbre, mais en renvoie un nouveau. On pourrait donc s'inquiéter de ses performances : est-ce que tout l'arbre est copié à chaque fois pour rendre cela possible ? En regardant le code, vous pouvez trouver la réponse : seules les branches qui sont sur le chemin pour aller de la racine à l'élément qu'on a inséré ont été recréées. Les performances sont donc plutôt bonnes : avec une liste, il aurait fallu en moyenne recréer la moitié de la liste, alors que là on ne recopie que quelques branches de l'arbre.
D'ailleurs, on peut se servir de l'arbre binaire de recherche pour faire un tri plus rapide que le tri par insertion : au lieu d'insérer les éléments dans une liste triée, on les insère dans un ABR (donc trié lui aussi). Pour cela, on doit coder deux fonctions auxiliaires : une fonction construireArbre, qui construit un arbre binaire de recherche à partir d'une liste triée, et d'une fonction aplatir qui renvoie une liste triée constituée de tous les éléments d'un arbre binaire.
1 2 3 4 5 6 7 8 9 10 11 12 | -- construire un arbre à partir d'une liste construireArbre :: (Ord a) => [a] -> Arbre a construireArbre = foldr inserer Feuille aplatir :: Arbre a -> [a] aplatir = foldArbre (\e g d -> g ++ [e] ++ d) [] -- version sans foldArbre : aplatir' Feuille = [] aplatir' (Branche e g d) = aplatir' g ++ [e] ++ aplatir' d triABR :: (Ord a) => [a] -> [a] triABR = aplatir . construireArbre |
Une dernière opération utile sur les ABR est la suppression d'un élément (autrement dit, créer un nouvel arbre auquel on a enlevé un élément donné). C'est une opération un peu plus délicate à effectuer, et je vous invite à y réfléchir et à essayer de la coder vous-même avant de lire la solution (avec du papier et un crayon, c'est plus facile pour dessiner les arbres). Puisqu'on sait déjà trouver un élément dans un arbre, on peut se ramener au cas où l'élément que l'on souhaite supprimer se trouve à la racine. Ensuite, on doit envisager différents cas suivant le ce qu'on trouve en allant à droite et à gauche : si on trouve deux Feuilles, il suffit de remplacer la racine par une Feuille. Si on trouve une Feuille et une Branche, on remplace la racine par cette Branche. Le cas compliqué est celui où on a deux branches. On doit donc chercher un nouvel élément qui servira de racine : pour cela, on prend le plus grand élément de la branche de gauche.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | supprimerPlusGrand (Branche e g Feuille) = (g,e) supprimerPlusGrand (Branche e g d) = let (d',grand) = supprimerPlusGrand d in (Branche e g d', grand) supprimerRacine (Branche _ Feuille Feuille) = Feuille supprimerRacine (Branche _ g Feuille) = g supprimerRacine (Branche _ Feuille d) = d supprimerRacine (Branche _ g d) = Branche e' g' d where (g',e') = supprimerPlusGrand g supprimer _ Feuille = Feuille supprimer e (Branche f g d) | e == f = supprimerRacine (Branche f g d) | e < f = Branche f (supprimer e g) d | e > f = Branche f g (supprimer e d) |
On a donc vu comment utiliser les arbres binaires de recherche comme structure de données pour représenter des ensembles, et les opérations qui vont avec. Un problème se pose cependant. Quand on introduit successivement des éléments déjà ordonnés dans un ABR, à chaque fois l'élément qu'on insère va se retrouver à droite de l'arbre. Donc, tous les éléments vont être concentrés d'un côté, ce qui fait qu'on se retrouve finalement avec des opérations de recherche, d'insertion et de suppression inefficaces. Par exemple, avec un arbre à $2^n$ éléments, il faut $2^n$ opérations dans le pire des cas pour trouver si un élément est dans l'arbre. Au contraire, si l'arbre est équilibré (c'est-à-dire si la feuille qui est à la plus grande profondeur n'a pas une profondeur très différente de celle qui est le plus proche de la racine), il va avoir à peu près une profondeur de $n$, et donc il faudra $n$ opérations pour rechercher un élément. Il existe des arbres où les opérations de modification rééquilibrent automatiquement l'arbre : c'est le cas des arbres AVL et des arbres rouge-noir.
Représenter des expressions mathématiques
On peut aussi utiliser des types algébriques récursifs pour représenter un petit langage de programmation. Par exemple, ici on va créer un type qui représente des expressions mathématiques simples (addition, multiplication, soustraction). Le constructeur Litt permet d'utiliser des valeurs littérales dans les expressions (par exemple Lit 42), et Var sert à représenter une variable.
1 2 3 4 5 6 7 8 9 | data Expr = Litt Integer | Var String | Add Expr Expr | Mul Expr Expr deriving (Eq, Show) -- Exemple : cette expression correspond à x^2+7x+1 test = Add (Mul (Var "x") (Var "x")) (Add (Mul (Litt 7) (Var "x")) (Litt 1)) |
On peut commencer par coder une fonction pour évaluer une expression, c'est-à-dire donner sa valeur. Elle prend en argument un contexte, qui donne la valeur des variables utilisées, et bien sûr une expression. Pour des raisons de simplicité, on ne s'occupera pas de la gestion des erreurs, par exemple si on ne connaît pas la valeur d'une variable utilisée.
1 2 3 4 5 6 7 8 9 10 | -- Cette fonction renvoie la valeur d'une variable dans le contexte ctx valeur ctx var = snd $ head $ filter (\(nom,_) -> nom == var) ctx eval ctx (Add a b) = eval ctx a + eval ctx b eval ctx (Mul a b) = eval ctx a * eval ctx b eval ctx (Litt a) = a eval ctx (Var s) = valeur ctx s -- On évalue l'expression test pour x=5 valTest = eval [("x",5)] test |
Le code pour évaluer nos expressions est donc plutôt simple. En revanche, la syntaxe pour écrire les expressions est très lourde : on pourrait vouloir créer un parser pour nos expressions mathématiques, qui transforme une chaîne de caractère comme (x^2+72x+2)(20+y+xy) en la valeur du type Expr qui correspond. Si vous cherchez quelque chose à faire, ça peut être amusant de regarder comment faire. En tout cas, vous verrez dans la prochaine sous-partie une astuce amusante pour ne pas avoir à faire ça vous même.
On peut aussi coder des fonctions qui font des transformations sur les expressions : développer, évaluer tout ce qui peut être évalué sans connaître la valeur de toutes les variables, réduire une expression (regrouper les termes en x ensembles, puis les termes en $x^2$, …
1 2 3 4 5 6 | developper (Add x y) = Add (developper x) (developper y) developper (Mul x y) = case (developper x, developper y) of (Add a b,y') -> developper (Add (Mul a y') (Mul b y')) (x', Add a b) -> developper (Add (Mul x' a) (Mul x' b)) (x',y') -> Mul x' y' developper e = e |
Il y a beaucoup de choses intéressantes à faire à partir de ça : vous pouvez coder d'autres fonctions de manipulation des expressions mathématiques (par exemple, mettre les expressions dans une forme correcte ou essayer de factoriser une expression) ou bien rajouter des opérations à ce tout petit langage de base pour créer un petit langage de programmation.
Des instances de classes de types
Maintenant que vous pouvez créer vos propres types, vous aurez probablement besoin de créer des instances de classes de types qui leur correspondent. Par exemple, on ne peut pas savoir si des éléments de notre type Parfum sont égaux, puisqu'on n'a pas d'instance de Eq pour Parfum. Cette sous-partie va donc vous apprendre à définir des instances d'une classe de type.
deriving : une instance sans se fatiguer
La manière la plus simple de créer une instance est d'utiliser deriving : on a déjà utilisé cette technique avec Show, pour pouvoir afficher les valeurs dans ghci. Par exemple, le code ci-dessous permet de déclarer un type Parfum, et en même temps une instance de Eq qui va avec :
1 2 3 4 | data Parfum = Chocolat | Vanille | Framboise deriving Eq |
On peut dériver des instances de plusieurs classes en utilisant des parenthèses :
1 2 3 4 | data Parfum = Chocolat | Vanille | Framboise deriving (Eq, Show, Read) |
1 2 3 4 5 6 7 8 | *Main> show Framboise "Framboise" *Main> read "Framboise" :: Parfum Framboise *Main> Framboise == Chocolat False *Main> Vanille == Vanille True |
Cependant, il y a quelques limitations : d'abord, on ne peut dériver que des instances de classes "simples", comme Eq, Ord, Read ou Show. Ensuite, l'instance générée n'est pas toujours satisfaisante : par exemple, on pourrait aimer que l'instance de Eq pour les arbres binaires de recherche ne vérifie pas si les deux arbres ont la même forme et les mêmes éléments, mais juste si ils contiennent les mêmes éléments : dans ces deux cas, on doit déclarer l'instance de façon manuelle.
Créer une instance
Instances simples
La première chose à faire quand on veut créer une instance d'une classe de type est de lire la documentation. En effet, elle indique les fonctions qui doivent être déclarées pour que l'instance soit valide. De plus, parfois, les classes de types fournissent des déclarations par défaut pour certaines fonctions de la classe. Par exemple, la classe Eq fournit une fonction (==) et une fonction (/=). Cependant, il est très facile de définir == à partir de /= et inversement : ces deux fonctions ont donc une déclaration par défaut qui utilise l'autre, et ce serait inutile de déclarer les deux.
Une fois que vous avez trouvé les informations nécessaires, vous pouvez déclarer votre instance (avant cela, enlevez le deriving Eq de la déclaration de Parfum).
1 2 3 4 5 | instance Eq Parfum where Chocolat == Chocolat = True Vanille == Vanille = True Framboise == Framboise = True _ == _ = False |
Maintenant, vous avez une préférence pour les parfums des glaces, donc vous aimeriez bien les ordonner, de celui que vous aimez le plus à celui que vous aimez le moins. Pour cet exemple, on va dire que dans l'ordre, les parfums préférés sont Framboise, Chocolat et Vanille mais je ne veux pas déclencher une guerre de religion sur les parfums de glace, donc si vous voulez un autre ordre, vous avez le droit de le changer.
Donc, première étape, on va chercher la documentation de Ord. Cette classe de type est définie dans le Prelude, donc sa documentation devrait se trouver ici : http://www.haskell.org/ghc/docs/6.10.4/html/libraries/base/Prelude.html. Ensuite, regardez dans la partie Synopsis : vous trouverez une ligne qui ressemble à class Eq a => Ord a where. C'est ce que vous cherchez, donc cliquez sur le mot Ord. Vous trouvez une liste de fonctions qui font parties de la classe, et cette phrase :
Minimal complete definition: either
compareor<=. Usingcomparecan be more efficient for complex types.
documentation
Cette phrase nous indique donc qu'il suffit de définir soir la fonction compare, soit l'opérateur <=. Pour cet exemple, on va choisir de définir <= :
1 2 3 4 5 6 | instance Ord Parfum where _ <= Framboise = True -- La Framboise, c'est le mieux Chocolat <= Chocolat = True Vanille <= Vanille = True Vanille <= Chocolat = True _ <= _ = False -- Dans le reste des cas, c'est faux |
Voilà, vous savez définir des classes de types pour des types simples.
Pour des types paramétrés
Maintenant, on veut définir une instance d'Eq pour notre type Arbre : deux arbres binaires de recherche sont égaux si et seulement s'ils contiennent les mêmes éléments (on ne s'intéresse donc pas à la structure de l'arbre). Cependant, en voulant définir cette instance, on rencontre un problème : les éléments du type Arbre a (éléments de type a) ne sont pas forcément membres de la classe Eq. On doit donc indiquer une condition pour que l'instance soit définie :
1 2 | instance (Eq a) => Eq (Arbre a) where a == b = aplatir a == aplatir b |
Cette déclaration se lit "Si on peut comparer des a pour l'égalité, on peut comparer des Arbre a pour l'égalité". Parfois, vous aurez besoin de plusieurs conditions : vous pouvez les séparer par des virgules. Notez aussi qu'on ne peut pas écrire instance (Eq a) => Eq Arbre : Arbre n'est pas un type mais un constructeur de type, une valeur de type Arbre ne peut pas exister.
Des instances pour le type Expr
Nous allons définir deux instances utiles pour le type Expr.
Afficher des expressions mathématiques
Pour l'instant, quand on essayer d'afficher des valeurs de type Expr, on obtient un résultat illisible, comme par exemple Mul (Add (Mul (Var "x") (Var "x")) (Add (Mul (Litt 7) (Var "x")) (Litt 1))) (Add (Add (Mul (Mul (Mul (Var "x") (Var "x")) (Mul (Var "x") (Var "x"))) (Var "x")) (Mul (Litt 3) (Var "x"))) (Litt 7)) au lieu de (x^2+7*x+1)*(x^5 + 3*x + 7). On va donc essayer de créer une instance de Show pour résoudre ce problème. On va commencer par une idée simple : remplacer les Mul par des * et les Add par des +. On va aussi rajouter des parenthèses autour de chaque expression pour éviter les problèmes de priorités. On définit aussi quelques expressions pour tester notre instance :
1 2 3 4 5 6 7 8 9 | instance Show Expr where show (Litt a) | a < 0 = "("++ show a ++ ")" | otherwise = show a show (Var s) = s show (Add a b) = "(" ++ show a ++ "+" ++ show b ++ ")" show (Mul a b) = "(" ++ show a ++ "*" ++ show b ++ ")" expr1 = Add (Add (Mul (Var "x") (Var "x")) (Mul (Litt 3) (Var "x"))) (Litt 7) expr2 = Add (Add (Mul (Var "x") (Var "x")) (Mul (Litt 3) (Mul (Var "y") (Var "y")))) (Litt 2) |
On peut comparer les résultats :
1 2 3 4 5 6 | ### Avant Main> expr1 * expr2 Mul (Add (Add (Mul (Var "x") (Var "x")) (Mul (Litt 3) (Var "x"))) (Litt 7)) (Add (Add (Mul (Var "x") (Var "x")) (Mul (Litt 3) (Mul (Var "y") (Var "y")))) (Litt 2)) ### Après Main> expr1 * expr2 ((((x*x)+(3*x))+7)*(((x*x)+(3*(y*y)))+2)) |
C'est un peu mieux, mais il y a des parenthèses en trop : par exemple, Add (Litt 1) (Add (Litt 2) (Litt 3)) est affiché 1+(2+3), alors qu'on pourrait afficher 1+2+3. Cependant, on ne peut pas simplement enlever les parenthèses partout : elles sont nécessaires quand on veut afficher une addition à l'intérieur d'une multiplication. On peut donc mettre un niveau de priorité : le niveau de priorité de l'addition est 0, celui de la multiplication est 1, et on ne peut enlever les parenthèses que si le niveau de priorité de ce qu'on veut afficher est supérieur ou égal au niveau de priorité courant. Cependant, on ne peut pas magiquement rajouter un paramètre pour ça à show : on va devoir créer une autre fonction.
1 2 3 4 5 6 7 8 9 10 11 12 | -- Cette fonction ajoute les parenthèses si nécessaire addPar k n s | k <= n = s | otherwise = "(" ++ s ++ ")" showExpr k (Add a b) = addPar k 0 (showExpr 0 a ++ "+" ++ showExpr 0 b) showExpr k (Mul a b) = addPar k 1 (showExpr 1 a ++ "*" ++ showExpr 1 b) showExpr _ (Var s) = s showExpr _ (Litt a) | a < 0 = "("++ show a ++ ")" | otherwise = show a instance Show Expr where show e = showExpr 0 e |
En testant dans ghci, on obtient le résultat qu'on attendait :
1 2 | *Main> expr1 * expr2 (x*x+3*x+7)*(x*x+3*y*y+2) |
Combiner les expressions
On peut additionner, soustraire et multiplier des expressions : il est donc naturel de créer une instance de Num pour Expr. Si on regarde la documentation, on voit qu'on doit définir en plus de ces trois opérations les fonctions fromInteger, signum et abs. fromInteger correspond très bien au constructeur Litt, et on va ignorer abs et signum pour l'instant. De plus, on voit que notre type doit obligatoirement pouvoir être affiché (Show) et comparé (Eq) : ces conditions sont déjà réalisées. On peut donc déclarer notre instance :
1 2 3 4 5 | instance Num Expr where (+) = Add (*) = Mul negate = Mul (Litt (-1)) fromInteger = Litt |
On a préféré déclarer negate plutôt que (-) : la documentation signale que l'on peut déclarer l'un ou l'autre, au choix. Vous aurez un avertissement du compilateur en chargeant ce programme puisqu'il manque les méthodes signum et abs.
L'avantage de cette instance, c'est qu'on peut écrire des expressions avec les opérations mathématiques normales. On profite même de l'opérateur puissance alors qu'on n'a rien défini pour que ça marche !
1 2 3 4 | x = Var "x" y = Var "y" exprTest = 3*x^5 + 7*x + 9 + 12 * x * y |
1 2 3 4 | *Main> eval [("x",5),("y",12)] exprTest 10139 *Main> eval [("x",5),("y",12)] (exprTest ^ 2) 102799321 |
Créer des classes de types
Vous pouvez aussi créer vos propres classes de types. Par exemple, dans certains langages, on peut utiliser if sur d'autres choses que des booléens : une conversion en booléen est réalisée. Par exemple, une liste vide ou le nombre 0 donneraient False, et une liste non vide donnerait True. On définit donc notre classe comme ceci :
1 2 | class OuiNon a where toBool :: a -> Bool |
Voilà, ce n'est pas compliqué : on indique le nom de la classe de type, puis le type des différentes fonctions qui devront être fournies.
Ensuite, on rajoute quelques instances :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | instance OuiNon Bool where toBool = id instance OuiNon Int where toBool 0 = False toBool _ = True instance OuiNon Integer where toBool 0 = False toBool _ = True instance OuiNon [a] where toBool [] = False toBool _ = True instance OuiNon (Arbre a) where toBool Feuille = False toBool _ = True instance OuiNon (Maybe a) where toBool Nothing = False toBool _ = True |
On peut alors tester le code :
1 2 3 4 5 6 7 8 9 10 | Main> toBool Nothing False Main> let (a,b) = (0,1) Main> let f n = if (toBool n) then "YEAH !" else "NON :(" Main> f a "NON :(" Main> f b "YEAH !" Main> f [] "NON :(" |
Il est possible de créer des définitions plus compliquées, en ayant par exemple des conditions ou des définitions par défaut pour certaines fonctions, comme par exemple avec la définition de la classe Ord, tirée directement du code source du Prelude (vous pouvez regarder le code source des fonctions qui vous intéressent en cliquant sur le lien "Source" à côté de la documentation de la fonction) :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | -- Pour qu'on puisse déclarer une instance de Ord, on a besoin d'une instance de Eq class (Eq a) => Ord a where -- on définit les fonctions nécessaires et leurs types compare :: a -> a -> Ordering (<), (<=), (>), (>=) :: a -> a -> Bool max, min :: a -> a -> a -- Les définitions par défaut : compare est défini en fonction de <= et inversement compare x y = if x == y then EQ else if x <= y then LT else GT x < y = case compare x y of { LT -> True; _ -> False } x <= y = case compare x y of { GT -> False; _ -> True } x > y = case compare x y of { GT -> True; _ -> False } x >= y = case compare x y of { LT -> False; _ -> True } max x y = if x <= y then y else x min x y = if x <= y then x else y |
Vous pouvez lire le code original (et les commentaires associés) ici : http://www.haskell.org/ghc/docs/6.10.4/html/libraries/base/src/GHC-Classes.html#Ord
Voilà, ce chapitre est terminé. Dans le prochain chapitre, vous allez voir comment découper votre code en modules, créer des programmes qui interagissent avec l'extérieur et comment les compiler.