Le théorème de Pythagore est à la fois très connu mais aussi essentiel dans nombres de domaines que ce soit en mécanique, en géométrie ou en algèbre linéaire. Il fut amélioré par certains savants du moyen-âge mais donna aussi naissance à de nouveaux problèmes qui ne trouveront de solution qu'à l'orée du XXIème siècle. Le présent chapitre vous propose d'aller voir ces différentes extensions du théorème de Pythagore.
- Norme euclidienne d'un espace à n dimensions
- Trigonométrie et théorème d'Al-Kashi
- Triplets pythagoriciens et dernier théorème de Fermat
Norme euclidienne d'un espace à n dimensions
De quoi parle-t-on ?
Nous allons ici chercher à déterminer la norme euclidienne d'un vecteur dans un repère orthonormé. Mais ne fuyez pas, je vais vous expliquer de quoi il s'agit. Un vecteur, en géométrie, ce n'est rien de plus qu'une flèche comme ci-dessous :

Pour simplifier, on pourrait dire qu'il s'agit d'un segment muni d'un sens. Le vecteur ci-dessus se note $\vec {AB}$ et symbolise un déplacement de A vers B, ce qui n'est pas la même chose que le vecteur $\vec {BA}$ qui représente le déplacement inverse de B vers A. Chercher à calculer sa norme, ce n'est rien de plus que de chercher sa longueur AB. Le terme exact est norme euclidienne, car il existe des géométries calculant les longueurs de façon très particulière. Ce qui est commode, c'est d'utiliser les vecteurs dans un repère orthonormé. Qu'est-ce qu'un repère orthonormé ? Rien de plus que les axes d'un graphique. Mais attention, il faut que les axes soient perpendiculaires et gradués de la même façon. Exemple :

Les points A et B peuvent chacun être situés à l'aide de deux nombres appelés coordonnées du point. Ainsi, le point A ci-dessus a pour coordonnées (2 ; 4) alors que B a pour coordonnées (6 ; 6). De façon plus générale, ces coordonnées sont notées A(xA ; yA) et B(xB ; yB). De la même manière, un vecteur peut aussi être muni de coordonnées, mais celles-ci ne représentent pas sa position dans le repère mais le déplacement qu'il symbolise. Par exemple, le vecteur $\vec {AB} = \vec v$ ci-dessus a pour coordonnées $\binom{4}{2}$, car il se déplace de 4 carreaux vers la droite et de 2 carreaux vers le haut. Le vecteur $\vec{BA}$ aurait eu pour coordonnées $\binom{-4}{-2}$ car il se serait déplacé de 4 carreaux vers la gauche et de 2 carreaux vers le bas. Enfin, la norme du vecteur $\vec {AB} = \vec v$ se note $||\vec {AB}|| = ||\vec v||$.
Norme euclidienne en dimension 2
Notre but est donc de connaître la longueur de ce vecteur $\vec {AB}$ à partir des coordonnées de A et B. L'astuce consiste à introduire un point H afin de former un triangle rectangle :
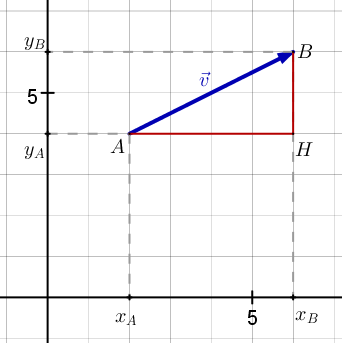
On peut alors lire facilement que AH = 4 et BH = 2 (il n'y a pas d'unité ici). En utilisant le théorème de Pythagore on obtient :
Ce qui se note également $|| \vec{AB} ||=\sqrt {20}$. Maintenant, réfléchissons. D'où vient cette valeur AH=4 ? Nous savions que xA=2 et xB=6, donc ce 4 a été obtenu par la soustraction $AH = x_B - x_A = 6 - 2 = 4$. De même, $BH = y_B - y_A = 6 - 4 = 2$. Donc, si $AH = x_B - x_A$ et $BH = y_B - y_A$, alors le théorème de Pythagore nous donne :
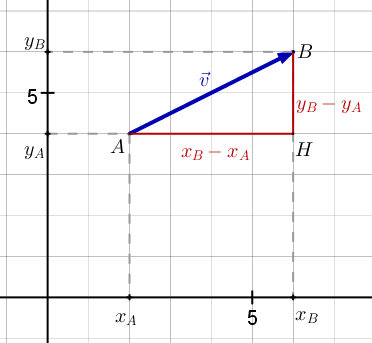
Nous avons donc les formules suivantes pour calculer la norme euclidienne d'un vecteur dans un espace à 2 dimensions :
Si A et B sont deux points de coordonnées $(x_A ; y_A)$ et $(x_B ; y_B)$ alors on a :
Autrement dit, si on a un vecteur $\vec v \binom x y$, alors :
Pour être rigoureux, il faudrait dire que $AH = |x_B - x_A|$ et $BH = |y_B - y_A|$. Mais les valeurs absolues devenant inutiles lors de l'application des carrés et alourdissant l'explication, le choix a été fait de ne pas les mentionner afin de ne pas ajouter des difficultés supplémentaires.
Norme euclidienne en dimension 3
Cette formule peut-elle se généraliser à des espaces de plus grande dimension ?
Pour répondre à cette question, revenons quelques instants sur un exercice précédent : le calcul de la diagonale d'un pavé droit.
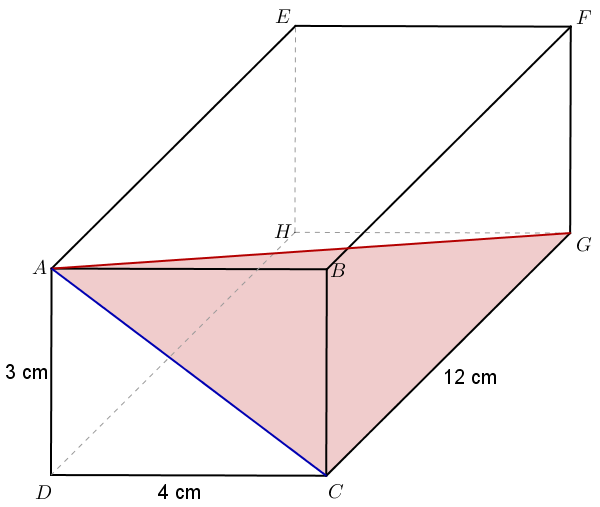
Nous avions alors calculé la longueur de la diagonale [AC] à l'aide de la formule $AC^2 = DA^2 + DC^2$, pour ensuite obtenir la longueur AG à l'aide de la formule $AG^2 = AC^2 + CG^2$. Mais si dans la deuxième égalité, nous remplaçons $AC^2$ par ce qui est donné dans la première, nous obtenons une sorte de "formule de Pythagore 3D" :
Ce qui peut également se formuler ainsi (en notant $d$ la diagonale du pavé, $l$ sa largeur, $L$ sa longueur et $h$ sa hauteur) :
Gardez cette formule dans un coin de votre tête et revenons à notre problème : calculer la norme d'un vecteur dans un espace à trois dimensions. Voilà pour commencer à quoi cela peut ressembler :
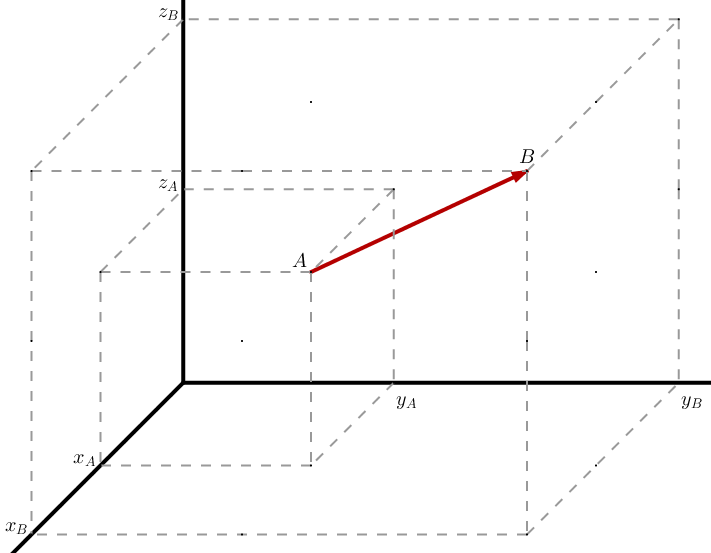
Il faut cette fois non plus 2 nombres pour situer un point, mais 3 ! Les coordonnées de A et B sont donc notées $A(x_A ; y_A ; z_A)$ et $B(x_B ; y_B ; z_B)$. Pour connaître la norme du vecteur $\vec {AB}$, nous allons faire apparaître un pavé droit ayant [AB] comme diagonale :
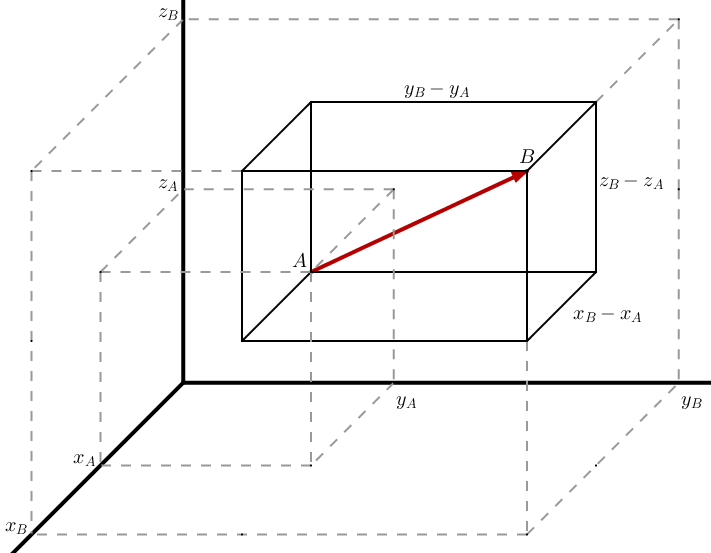
Pour connaître les dimensions de ce pavé, il suffit d'effectuer les soustractions habituelles : $x_B - x_A$, $y_B - y_A$ et $z_B - z_A$. C'est donc maintenant que nous allons faire appel à notre super formule de Pythagore 3D et y injecter nos soustractions :
Nous obtenons donc deux nouvelles formules très proches des formules obtenues précédemment :
Si A et B sont deux points de coordonnées $(x_A ; y_A ; z_A)$ et $(x_B ; y_B ; z_B)$ alors on a :
Autrement dit, si on a un vecteur $\vec v \begin{pmatrix}x\\y\\z\end{pmatrix}$, alors :
Norme euclidienne en dimensions 4, 5, 6 …
Même si cela semble difficile à visualiser, les mathématiciens actuels aiment travailler avec des espaces à 4, 5, 6 voire n dimensions (où n est un nombre potentiellement très grand). Il va devenir compliqué pour moi de réaliser les dessins explicatifs, mais vous devriez pouvoir vous en passer. Commençons par un espace de dimension 4 : vous aurez compris qu'il faudra 4 nombres dans les coordonnées des points et des vecteurs. Oublions nos points A et B, ne gardons que le vecteur $\vec v$. Celui-ci aura pour coordonnées :
Vous ne devriez pas avoir de peine à extrapoler la formule permettant de calculer la norme de notre vecteur :
Facile non ? On essaye avec 6 dimensions ? C'est parti mais avant cela, nous allons changer nos notations ou sinon nous risquons de nous emmêler les pinceaux dans l'alphabet (et puis ça deviendrait ridicule d'écrire les lettres dans le désordre). Chaque coordonnée sera notée à l'aide de la lettre $x$ à laquelle on adjoindra un numéro en indice. Ainsi, notre vecteur sera :
Et sa norme sera : $|| \vec v || = \sqrt{{x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2 + {x_5}^2 + {x_6}^2}$ Mais vous vous apercevez comme moi que cette formule devient longue à écrire, c'est pourquoi les mathématiciens ont inventé un symbole spécifique pour les additions à rallonge. Il s'agit de la lettre grecque sigma : $\sum$. Et voici ce que donne notre formule :
Tous les numéros ont été remplacés par la lettre $i$. On indique au-dessous du symbole $\sum$ la valeur minimale de $i$ (ici 1) et au-dessus sa valeur maximale (ici 6). Il devient alors très facile d'augmenter le nombre de dimensions à 7, 8, 9 ou 1000, puisqu'il suffit de modifier la valeur maximale. Ainsi, pour un espace de dimension $n$ (où $n$ est un nombre entier aussi grand que souhaité), la norme euclidienne d'un vecteur est donnée par la formule :
Avouez qu'en voyant cette formule pour la première fois, vous n'auriez jamais pensé qu'il s'agissait en fin de compte du théorème de Pythagore. 
Trigonométrie et théorème d'Al-Kashi
Cette partie va faire appel à des notions de trigonométrie, notamment le sinus, le cosinus et le cercle trigonométrique. Ce cours n'ayant pas vocation à couvrir tous les champs des mathématiques, je vous invite à consulter ce tutoriel si vous n'avez jamais manipuler ces notions.
Valeurs remarquables du cosinus et du sinus
Petits rappels
Nous allons déterminer les valeurs du cosinus et du sinus pour des angles de 30°, 45° ou 60°. Pour cela, nous allons avoir besoin du cercle trigonométrique. Sans faire un cours de trigonométrie, rappelons qu'un cercle trigonométrique est un cercle de rayon 1 dont le centre est le centre d'un repère orthonormé. Exemple :
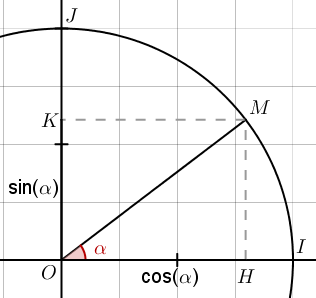
Sur ce cercle, si on place un point M et que l'on appelle $\alpha$ la mesure de l'angle $\widehat {IOM}$, alors on peut lire très facilement le cosinus et le sinus de $\alpha$. Il suffit pour cela de construire les points H et K, projetés orthogonaux de M sur l'axe des abscisses et sur l'axe des ordonnées. On a alors $OH = MK = \cos(\alpha)$ et $HM = OK = \sin(\alpha)$.
On peut dors et déjà appliquer le théorème de Pythagore puisque OMH est rectangle en H :
Cette fameuse formule trigonométrique permet de déterminer le sinus d'un angle connaissant son cosinus et réciproquement. Mais venons-en à des cas particuliers. Et tout d'abord, que valent le sinus et le cosinus d'un angle de 45 ° ?
L'angle de 45°
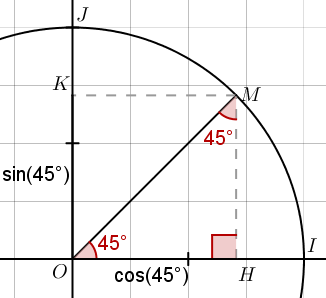
Si nous considérons un angle $\alpha$ de 45°, on constate rapidement que le triangle OHM est non seulement rectangle mais également isocèle. De là se dégagent deux conclusions assez évidentes :
- Le rectangle OHMK est en réalité un carré
- $OH=OK$ donc $\cos(45°) = \sin(45°)$
La plus intéressante est la première car nous avons établi une formule au chapitre précédent : les diagonales des carrés de côté $a$ mesurent $a \sqrt 2$ ! Et nous savons que la diagonale [OM] mesure 1 puisque c'est également un rayon du cercle trigonométrique. Nous aboutissons ainsi à l'équation : $a \sqrt 2 = 1$. Ne reste plus qu'à la résoudre pour trouver la longueur du côté $a$ :
Nous avons ainsi trouver une première valeur remarquable : $\color{red}\cos(45°) = \sin(45°) = {\sqrt 2 \over 2}$. Passons maintenant aux angles de 60° et 30°.
Les angles de 30° et 60°

Si nous considérons un angle $\alpha$ de 60° tout d'abord (le cas 30° étant symétrique), on constate que l'on obtient un triangle OMI équilatéral. En effet, $OI = OM$ donc le triangle OMI est toujours isocèle. Mais comme les angles à la base d'un triangle isocèle sont égaux, $\widehat {OMI} = \widehat {OIM} = {{180 - 60} \over 2} = 60°$. Là encore, deux conclusions s'imposent :
- H est le milieu de [OI] donc $OH = \frac{OI}{2}=\frac 1 2$ ;
- d'après le chapitre précédent, la hauteur d'un triangle équilatéral de côté 1 mesure $\frac {\sqrt 3} 2$.
Le théorème de Pythagore nous a ainsi permis de dire que $\sin(60°) = \frac{\sqrt 3}{2}$ et $\cos(60°) = \frac{1}{2}$. Si nous faisions la figure pour un angle de 30°, nous constaterions cette fois que OMJ serait équilatéral et donc, par symétrie, que $\cos(30°) = \frac{\sqrt 3}{2}$ et $\sin(30°) = \frac{1}{2}$.
Généralisation du Théorème de Pythagore
Le théorème
Le théorème de Pythagore est très utile, nous l'avons vu. Mais il a une limite importante : il faut absolument un angle de 90° dans le triangle où l'on souhaite l'appliquer. Heureusement, le théorème de Pythagore a connu des améliorations, sous l'Antiquité tout d'abord puis au Moyen-Âge. C'est ainsi que fut formulée le théorème de Pythagore généralisé, aussi appelé Loi des cosinus ou théorème d'Al-Kashi, en l'honneur d'un important mathématicien persan du XIVème-XVème siècle.

Pour utiliser le théorème d'Al-Kashi, il faut disposer des longueurs de deux côtés d'un triangle ainsi que de la mesure de l'angle situé entre ces deux côtés. Ce théorème permet de déterminer la longueur du troisième côté du triangle ou, inversement, si l'on connaît les trois côtés du triangle, de déterminer ses angles. Prenons un triangle ABC dans lequel on cherche la longueur CB, le théorème de Pythagore généralisé donne la relation suivante :
Dans un triangle rectangle, la fin de cette formule ($- 2 \times AB \times AC \times \cos(\widehat{BAC})$) n'apparaît pas car le cosinus d'un angle droit vaut 0.
Un exemple
Voyons maintenant ce que donne ce théorème dans le triangle ci-dessous :
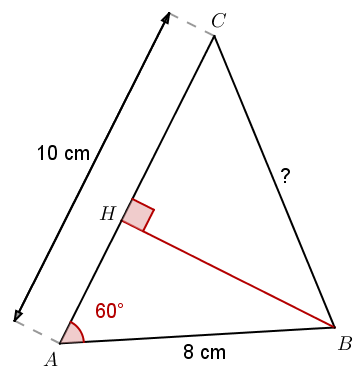
Il suffit, pour commencer, de remplacer chaque longueur par sa mesure :
Or nous avons vu que le cosinus d'un angle de 60° vaut 0,5. Il suffit donc désormais de calculer cette expression :
Une démonstration
Voyons maintenant comment parvenir à cette formule. Vous aurez remarqué que, dans la figure précédente, j'avais fait apparaître la hauteur [BH]. La raison est simple : il s'agit de faire apparaître des triangles rectangles pour pouvoir utiliser à la fois le théorème de Pythagore classique et les formules de trigonométrie. Ainsi, le théorème de Pythagore nous permet de calculer CB dans le triangle CBH : $CB^2 = CH^2 + HB^2$. Problème, nous ne connaissons pas la hauteur BH (entre autres). Mais celle-ci peut se calculer (toujours avec notre ami Pythagore) dans le triangle AHB : $HB^2 = AB^2 - AH^2$. En injectant cette deuxième formule dans la première, on obtient donc :
Mais nous sommes toujours face à un problème : nous ne savons pas où se situe le point H. C'est là qu'interviennent nos formules trigonométriques. Nous connaissons l'angle $\widehat {BAC}$ donc nous allons utiliser son cosinus : $\cos(\widehat{BAC}) = \frac {AH}{AB}$. Ce qui peut également s'écrire $\color{purple} AH = AB \cos(\widehat{BAC})$. Nous avons une formule pour $AH$, reste à en trouver une pour $CH$. Ce n'est pas le plus compliqué : $CH = AC - \underline{AH} = \color{purple}AC - AB \cos(\widehat{BAC})$.
Pour les triangles obtusangles, c'est à dire ceux ayant un angle aigu, la hauteur "sort" du triangle. On a alors : $CH = AH - AC$. Cette différence n'ayant pas d'impact sur le reste de la démonstration, nous allons la négliger.
Enfin, nous allons réutiliser la formule rouge dans laquelle nous remplacerons $AH$ et $CH$ par les deux formules violettes précédentes.
Vous aurez remarqué que l'un des carrés, celui souligné d'une accolade, est devenu un peu compliqué. Nous allons donc développer son écriture à l'aide de l'identité remarquable $(a+b)^2 = a^2 + 2ab + b^2$.
Après développement, les termes $AB \cos(\widehat{BAC})$ se suppriment et nous obtenons enfin la formule tant recherchée, celle du Théorème de Pythagore généralisé.
Triplets pythagoriciens et dernier théorème de Fermat
Sur les triplets pythagoriciens
Des triplets en pagaille
Nous avons déjà vu ce qu'était un triplet pythagoricien et j'espère que vous aurez retenu le fameux triplet (3;4;5). Mais peut-être avez-vous remarqué au cours des précédents exemples que j'ai utilisé d'autres triplets ? Ainsi, lors du calcul de la diagonale d'un rectangle j'avais utilisé le triplet (8;15;17) et pour la diagonale du pavé ou la hauteur du triangle isocèle c'était le triplet (5;12;13) qui avait eu ma préférence.
Combien existe-t-il de triplets pythagoriciens ?
La réponse est simple : une infinité. Prenons par exemple le triplet pythagoricien (3;4;5). Si l'on multiplie chaque nombre par 4 on obtient un nouveau triplet (12;16;20) lui aussi pythagoricien :
En multipliant par 2, 3, 5, 6 ou 7515, nous aurions pu imaginer autant de nouveaux triplets que souhaité. Ainsi, les triplets (6;8;10), (9;12;15), (12;16;20), (15;20;25) … sont tous pythagoriciens car ce ne sont rien de plus que des ersatz du triplet originel (3;4;5). Pour s'en convaincre, il suffit de prendre un triplet (x;y;z) pythagoricien, ce qui signifie que $x^2+y^2=z^2$. Si l'on multiplie chacun des nombres par un nombre entier k, on obtient ainsi un nouveau triplet (kx;ky;kz) et on remarque alors que :
Autrement dit, le nouveau triplet vérifie l'équation $(kx)^2+(ky)^2=(kz)^2$, il est lui-aussi pythagoricien. Mais on peut restreindre le nombre de triplets aux cas les plus simples, c'est-à-dire qui ne sont pas tous multiples d'un même nombre. On dit alors que les trois nombres composant le triplet sont premiers entre eux et que le triplet est primitif.
Déterminer les triplets primitifs
Alors combien existe-t-il de triplets pythagoriciens primitifs ?
Eh bien toujours une infinité, malheureusement. Mais il y a toutefois un point positif : il est potentiellement possible de déterminer tous les triplets pythagoriciens primitifs (si l'on a l'éternité devant soi bien sûr). Plus précisément, si l'on a deux nombres $a$ et $b$ premiers entre eux (qui n'ont pas de diviseur commun hormis 1) et de parités différentes, alors il est possible de générer un triplet pythagoricien primitif $(x;y;z)$ en calculant :
On peut en effet vérifier d'une part que : $z^2 = (a^2 + b^2)^2 = a^4 + 2 a^2 b^2 + b^4$ et d'autre part que :
Mieux encore ! Tout triplet pythagoricien peut s'écrire sous cette forme. Mais la démonstration complète exigeant une certaine technicité en arithmétique (ce qui n'est pas notre sujet principal), elle ne sera pas présentée ici.
Des triplets, des quadruplets ; des carrés, des cubes …
Quelques équations diophantiennes
On appelle équation diophantienne toute équation dont les coefficients et les solutions sont des nombres entiers ou fractionnaires, en l'honneur du mathématicien grec (quoique citoyen romain) Diophante d'Alexandrie. La relation de Pythagore $x^2 + y^2 = z^2$ est la plus célèbre d'entre elles mais elle a donné bien des idées à de nombreux autres mathématiciens.
Voici un exemple simple d'équation diophantienne élargissant le théorème de Pythagore : $x^2+y^2+z^2=t^2$. Cette équation diophantienne admet elle-aussi une infinité de solution. Par exemple $2^2+3^2+6^2=7^2$ ou encore $2^2 + 7^2 + 26^2 = 27^2$. Je vous laisse chercher d'autres solutions, c'est un jeu amusant et pas si compliqué (pour s'aider on pourra faire la liste des 10 premiers carrés et chercher l'opération permettant de passer d'un carré au suivant).
Il est possible d'obtenir d'autres équations diophantiennes en augmentant non plus le nombre de termes mais également les exposants, par exemple : $x^3+y^3+z^3=t^3$. Concernant cette équation, une anecdote raconte qu'un jour le grand mathématicien français Augustin Louis Cauchy reçut un manuscrit démontrant qu'elle n'admettait aucune solution. Cauchy prit alors sa plume et répondit simplement à son auteur : "$3^3 + 4^3 + 5^3 = 6^3$". En effet :
Le dernier théorème de Fermat
Si toutes les équations diophantiennes ne sont pas issues de l'égalité de Pythagore, il est en une, célébrissime, qui en est la très digne héritière. Je m'en vais vous conter son histoire. Diophante d'Alexandrie, dont nous avons déjà parlé, avait écrit une œuvre célèbre appelée les Arithmétiques et contenant 13 livres. Celui-ci n'était pas à proprement parler un traité de mathématiques, mais plutôt un recueil d'exercices contenant des solutions ingénieuses et souvent généralisables à des problèmes de même type. On y trouve par exemple le problème n°8 : "Diviser un nombre carré en une somme de deux carrés" ; autrement dit, "Trouver un triplet pythagoricien".
Mais à la chute de l'Empire romain, l’œuvre fut perdue par les européens et ne fut conservée que par les peuples orientaux (Byzantins, Arabes ou Persans). Elle ne refit son apparition dans nos contrées qu'au XVème siècle et mit de nombreuses décennies à être traduite du Grec et de l'Arabe vers le Latin, le Français, l'Anglais … d'ailleurs, sur les 13 livres écrits par Diophante, seuls 10 ont survécu au passage du temps.
L'arithmétique n'en demeura pas moins une branche mineure des mathématiques, jusqu'à ce qu'au XVIIème siècle, un magistrat français, passionné de Math, ne se plonge dans la lecture de cet ouvrage. Ce magistrat s'appelait Pierre Fermat et fut surnommé le "Prince des amateurs" pour son immense talent. Alors qu'il lisait et annotait les Arithmétiques de Diophante, Fermat en vint au problème n°8. Il en trouva bien entendu la solution et ajouta dans la marge les mots suivants :
"Un cube n'est jamais la somme de deux cubes, une puissance quatrième n'est jamais la somme de deux puissances quatrièmes … J'ai découvert une merveilleuse démonstration, mais la marge est trop étroite pour la contenir. "
En termes actuelles, Fermat écrit que les équations diophantiennes du type $x^n + y^n = z^n$ n'ont aucune solution lorsque $n > 2$. Cette affirmation constitue ce que l'on appelle le dernier théorème de Fermat. La méthode que Fermat affirme dans ses écrits avoir trouvée semble être sa fameuse méthode de la descente infinie : il montre que si un tel triplet (x;y;z) existe, alors il peut trouver un triplet strictement plus petit vérifiant lui-aussi l'équation, donc il peut trouver un autre triplet strictement plus petit vérifiant l'équation, donc il peut trouver un autre triplet strictement plus petit vérifiant l'équation, donc il peut trouver un autre triplet strictement plus petit vérifiant l'équation, … or avec les nombres entiers, il n'est pas possible de trouver infiniment des nombres plus petits. C'est ainsi que Fermat aurait prouver son théorème pour les cas $n = 3$ et $n = 4$.

Malheureusement, cette méthode ne marche plus à partir du rang $n = 5$. Alors Fermat a-t-il vendu la peau de l'ours avant de l'avoir tué ? Ou avait-il vraiment trouvé une "merveilleuse démonstration" ? Une chose est sûre : trois siècles plus tard, le dernier théorème résistait encore aux plus grands esprits des mathématiques. Des génies comme Euler, Dirichlet, Legendre ou Sophie Germain s'y étaient frottés avec plus ou moins de succès. Le théorème avait pu être démontré pour quelques exposants particuliers ou pour des groupes d'exposants, mais toujours pas pour tous les exposants.
Il fallut attendre 1993 pour qu'un mathématicien anglais (un peu fou) du nom de Andrew Wiles démontre le vieux théorème, après sept ans d'un travail acharné. Et encore ! Une erreur fut trouvée dans sa démonstration de plusieurs centaines de pages. Il fallut donc encore une année de labeur et de déprime au pauvre Wiles pour parvenir à une preuve irréfutable, mettant un terme à une quête vieille de plus de 350 ans.

A retenir :
- Dans un repère orthonormé, la norme d'un vecteur ou la longueur d'un segment se calcule à l'aide du théorème de Pythagore
- Le théorème de Pythagore amélioré ou théorème d'Al-Kashi peut s'appliquer dans n'importe quel type de triangle
- $cos(45°) = sin(45°) = {\sqrt 2 \over 2}$
- $cos(30°) = sin(60°) = {\sqrt 3 \over 2}$
- Il n'existe plus de triplets $(x,y,z)$ vérifiant $x^n + y^n = z^n$ au delà de $n = 2$.