L'isostasie : l'origine des mouvements verticaux de la lithosphère

Il est évident que la Terre n'est pas complètement plate : il existe des chaînes de montagne, des plaines, des bassins sédimentaires, des volcans, etc. Ces reliefs se forment essentiellement en augmentant ou en diminuant l'épaisseur de la croûte : les chaines de montagne et les volcans sont autant de phénomènes qui épaississent la croûte, là où les bassins sédimentaires, les dorsales et les rifts sont des zones où la croûte s'amincit. Sédimentation et érosion peuvent aussi épaissir la croûte ou l'amincir, en ajoutant ou enlevant des sédiments.

Mais cette accumulation de matière, ainsi que des effets thermiques, ont tendance à appuyer sur la lithosphère. Par exemple, les continents semblent monter ou descendre à la suite d'une variation de poids. Lors de la disparition d'un glacier, d'une montagne ou d'une couche sédimentaire, tout se passe comme si le continent remontait, libéré du poids imposé par le relief. Dans certaines situations, on observe l'effet inverse : le continent s'enfonce à la suite d'un ajout de poids, comme la formation d'un glacier, un empilement de couches sédimentaires ou la formation d'un relief. La lithosphère subit ainsi, sur de longues périodes, des mouvements verticaux particulièrement lents.

Pour expliquer ce genre de phénomène, les géologues ont inventé des modèles qui font tous appel à l'isostasie. Cette isostasie permet d'expliquer de nombreuses observations. Par exemple, elles expliquent pourquoi les chaines de montagnes ont une racine, une zone de croûte nettement plus épaisse que la normale. Elle permet aussi d'expliquer les modifications d'altitude liées à l'érosion, notamment pour les chaînes de montagnes (chose qui permet d'expliquer la formation de certains granites).

• L'isostasie : approche intuitive
• Modèles de l'isostasie
• Les mouvements causés par l'isostasie

L'isostasie : approche intuitive

Pour rappel, le manteau de la Terre a un comportement assez particulier : il a beau être solide, celui-ci est très déformable et se comporte comme un fluide sur de longues périodes de temps (millions d'années). Par "se comporte comme un fluide", on ne veut pas dire que celui-ci est liquide ou gazeux, mais que les roches du manteau sont suffisamment molles pour s'"écouler" lentement, un peu comme le ferait un vieux fromage qui commence à ramollir. Dans ces conditions, les lois de la mécanique des fluides s'appliquent au manteau.

Force de réaction

On se retrouve donc avec des morceaux de lithosphère solide et non-fluide (les plaques tectoniques) qui sont partiellement immergés dans un manteau fluide.

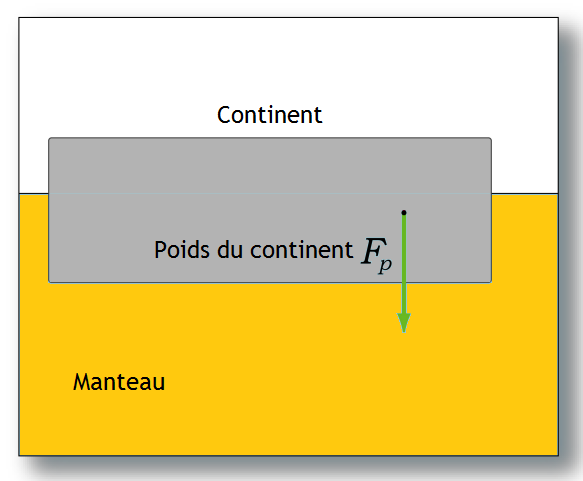
S'il n'y avait pas de force qui vienne compenser exactement l'effet du poids de la croûte, celle-ci coulerait dans le manteau plus fluide. Quelle est cette force qui vient contrecarrer le poids de la croûte en dehors des zones de subduction ? Et bien, c'est la même force que celle qui fait flotter les icebergs ou les navires sur l'océan. Et oui, vous avez bien lu : les plaques lithosphériques flottent sur le manteau grâce à la poussée d'Archimède.

Poussée d'Archimède

Pour rappel, le principe d’Archimède stipule que tout corps solide plongé dans un fluide subira une force, dirigée de bas en haut : la poussée d’Archimède. Elle a initialement été décrite dans les liquides, mais sa formulation actuelle fonctionne avec n'importe quel fluide, et les roches du manteau ne font pas exception.

Mais cette poussée d'Archimède ne suffit pas toujours à faire flotter un objet : il faut aussi que le solide soit moins dense que le fluide. Dans le cas contraire, le solide coule. Cela arrive dans certaines zones de subduction, où la plaque tectonique subductée, plus dense que le manteau, coule spontanément.

Mais dans tous les autres cas, le manteau est nettement plus dense que la croûte, et il en est de même pour la lithosphère, plus dense que l'asthénosphère. Dans ces conditions, la poussée d'Archimède contrecarre totalement le poids de la croûte : la croûte flotte sur le manteau, un peu comme la glace flotte sur l'eau.

D'après les lois de l'hydrostatique, plus le volume immergé est grand, plus la poussée d’Archimède sera grande elle aussi. Et cela vaut aussi pour la croûte immergée dans le manteau.

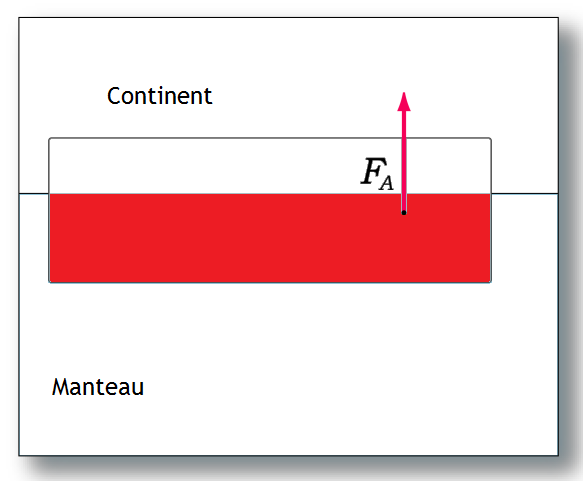
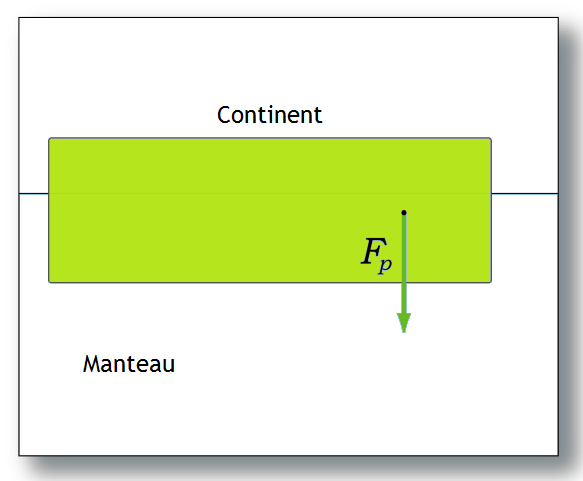
En comparaison, le poids d'un morceau de croûte (un continent) provient de tout son volume.

Équilibre isostatique

À l'équilibre, il n'y a pas de mouvement vertical de la lithosphère causé par la différence de densité : la force de flottabilité s'équilibre avec le poids de la croûte. Donc, quand le continent ne s'enfonce pas ou qu'il ne remonte pas, force de flottabilité et poids du continent sont égales. On parle d'équilibre isostatique.

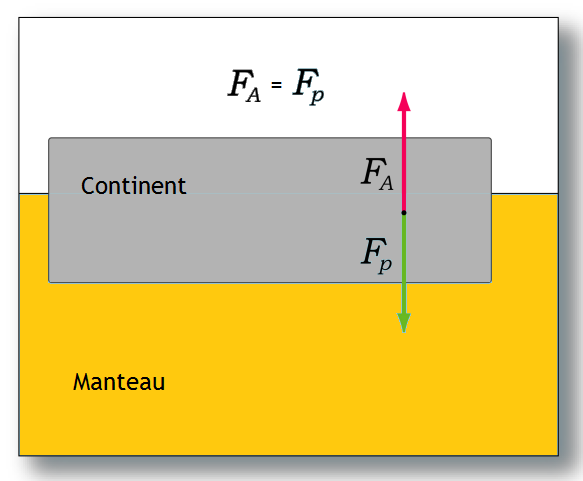
Cet équilibre permet de définir une surface de compensation, une surface horizontale où la pression est la même partout. Celle-ci se situe approximativement dans le manteau, et plus précisément dans l’asthénosphère.

Variations de poids

Maintenant, regardons ce qui se passe dans le cas d'un changement du poids de la lithosphère. Il existe de nombreux processus capables de changer ce poids en ajoutant de la masse : un apport de masse via la sédimentation, la formation d'une chaîne de montagne, la naissance d'un volcan, etc. L'érosion peut aussi retirer de la matière, diminuant ainsi le poids du continent. Bref, les mécanismes sont nombreux (et on donnera de nombreux exemples plus tard).

Intuitivement, plus on ajoute du poids, plus la croûte s'enfonce profondément dans le manteau. De même, diminuer le poids aura tendance à faire remonter la croûte. Pour résumer, un changement de masse est suivi par un mouvement vertical qui ramène la lithosphère à l'équilibre isostatique.

Dans ce qui va suivre, nous allons supposer que les ajouts ou retraits de matières sont très rapides. Le manteau n'a pas le temps de se déformer pendant que la masse du continent change, les mouvements du manteau étant très lents. Dans ces conditions, les mouvements verticaux qui ramènent la lithosphère à l'équilibre isostatique mettent du temps à se mettre en place. C'est souvent le cas dans la réalité, vu que les roches se déforment très lentement, et que les processus tectoniques ou d'érosion sont nettement plus rapides.

Si on ajoute de la masse sur le continent, son poids augmente. Par contre, le volume immergé dans le manteau et la poussée d’Archimède qui va avec ne changeront pas. En conséquence, le poids du continent deviendra supérieur à la poussée hydrostatique. La somme du poids et de la poussée donnera une force dirigée vers le bas : le continent s'enfonce.

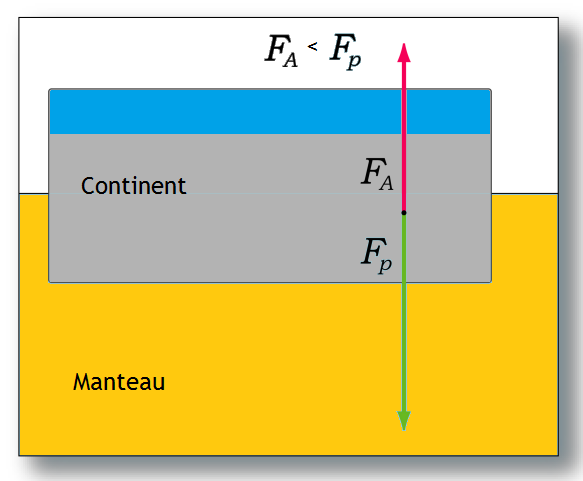
Lors de son enfoncement, le volume immergé dans le manteau augmentera, ce qui augmentera progressivement la poussée d’Archimède. Le processus continue jusqu'à ce que l'équilibre isostatique soit atteint. On peut tenir le même raisonnement dans le cas où on enlève de la masse sur le continent. Dans ce cas, le continent remonte jusqu'à ce que l'équilibre isostatique soit atteint.

Modèles de l'isostasie

Reste à formaliser cela mathématiquement, ce qu'ont fait certains géophysiciens. Il existe de nombreux modèles de l'isostasie, et je vais vous présenter les trois modèles les plus connus.

Ces trois modèles ne fonctionnent qu'une fois l'équilibre isostatique atteint : il ne doit pas y avoir de mouvement verticaux. Ainsi, ce modèle ne fonctionne que dans le cas où les chaînes de montagnes ont terminé de grandir : l'Himalaya ne respecte pas cette règle, par exemple. La chaîne de montagne doit aussi avoir une érosion assez faible, sans quoi elle rapetisse : l'équilibre isostatique est alors brisé par perte de masse.

Modèle de Airy

Le modèle de Airy suppose aussi que toute la lithosphère est une zone de densité uniforme, même dans les chaines de montagne ou les bassins sédimentaires. De plus, ce modèle suppose aussi que le manteau a une densité uniforme.

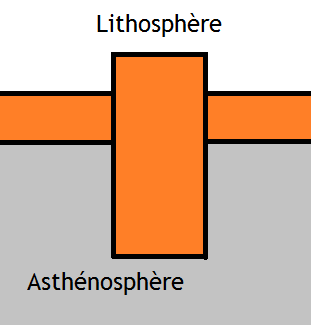
Le modèle d'Airy postule que la lithosphère est composée de plusieurs blocs de hauteurs différentes, mais de même densité. On suppose que les effets aux bords des blocs sont négligeables. De plus, toute variation d'épaisseur se répercute intégralement sur l'asthénosphère située en-dessous : le poids ne génère pas de contraintes horizontales, il ne "déborde" pas. Cette dernière hypothèse est appelée l'hypothèse d'équilibre isostatique local.

Montagnes

Ce modèle s'applique parfaitement aux épaississements de la lithosphère comme les chaines de montagnes et aux volcans éteints. En effet, les chaines de montagnes ne sont que la partie émergée d'un épaississement de la lithosphère : les montagnes ont des racines, des zones où la lithosphère est épaissie en profondeur et fait saillie dans l’asthénosphère. Le but du modèle d'Airy est de calculer la profondeur de cette racine, ce que nous allons faire maintenant.

Le modèle de Airy modélise la montagne ou le volcan d'une manière assez sommaire : un simple pavé.

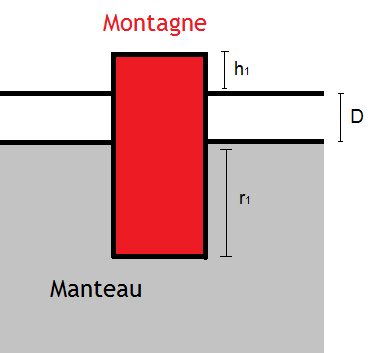
Pour simplifier, on suppose que la surface de compensation est située dans le manteau, qui a une densité constante. La conséquence directe de cette supposition est que la surface de compensation est située à la base de la racine de la chaîne de montagne. En effet, si on ajoute une hauteur $h$ de manteau avant d'arriver à la surface de compensation, on ajoute juste un terme $h \times d_a$ à la pression sous la croute normale, ainsi que sous la chaine de montagne : on reste sur une nouvelle surface de compensation.

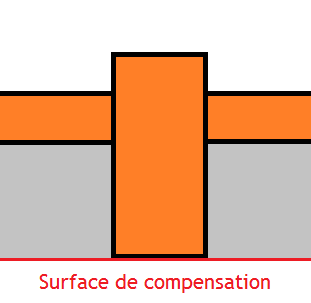
Reste à calculer la pression à la base de la chaîne de montagne, et la pression à la même profondeur dans le manteau (ces deux pressions sont situées sur la surface de compensation). On dispose des informations suivantes :

• la densité de la lithosphère et de l'asthénosphère, qu'on notera $d_l$ et $d_a$ ;
• l'épaisseur de la lithosphère, notée e ;
• la hauteur de la chaîne de montagne et de sa racine, notée $h_1$ et $r_1$.

De manière générale, la pression à la base d'un pavé de roche, est égale au poids du pavé divisé par la surface de sa base, ce qui donne : $\frac{M \times g}{S}$, avec $S$ la surface à la base du pavé, $M$ la masse du pavé, et $g$ l'accélération de la gravité. Vu que la masse est égale au produit de la densité par la hauteur, multipliée par la surface, la pression vaut donc : $D \times H \times g$, avec la densité $D$, la hauteur $H$. Dans les calculs qui suivent, $g$ étant constante nous l'omettrons dans les calculs.

Si vous faites les calculs vous-mêmes (rien de bien compliqué), vous obtiendrez : $P_g = d_l \times (h_1 + e + r_1)$.

Maintenant, nous allons regarder ce qui se passe à la même profondeur, mais cette fois-ci, sous la lithosphère normale (sans montagne ni bassin). La pression a cette profondeur est la somme de la pression causée par la lithosphère d'épaisseur e, et celle causée par le poids du manteau d'épaisseur $r_1$. On a donc une pression qui vaut : $e \times d_l + r_1 \times d_a$.

Or, selon le principe même de l'isostasie, les deux pressions égales : $( e \times d_l + r_1 \times d_a ) = d_l \times (h_1 + e + r1)$. On peut alors calculer la profondeur de la racine d'une chaîne de montagne en fonction de sa hauteur, et des densités :

Vu que les densités de la lithosphère et de l'asthénosphère sont connues, $\frac{d_l}{d_a - d_l}$ peut être calculée assez facilement. On trouve donc qu'à l'équilibre isostatique, la racine d'une montagne a une taille environ 6 fois plus importante que l'altitude de la montagne.

Bassins

Le modèle d'Airy s'applique aussi aux amincissements de la croûte, comme on peut en trouver dans les bassins sédimentaires. En-dessous de ces bassins, la lithosphère est amincie, le manteau remontant dans le vide laissé par la diminution d'épaisseur.

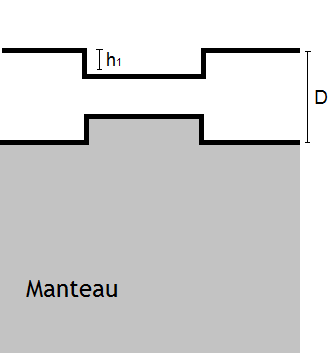
Les calculs qui vont suivre supposent que la surface de compensation est située à la profondeur normale de la lithosphère.

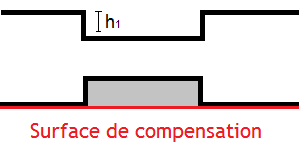
L'amincissement de la lithosphère en surface est noté $h_1$, tandis que l'amincissement en profondeur sera noté $r_1$. Cette fois, on calcule la pression à la base de la lithosphère normale, sans bassin ni montagne, qui vaut : $e \times d_l$. À la même profondeur, mais sous le bassin, la pression est la somme de la pression de la lithosphère amincie, et de l'asthénosphère qui a pris la place, ce qui donne : $(e - r_1 - h_1) \times d_l + r_1 \times d_a$. Les deux pressions sont égales, et quelques manipulations algébriques permettent de trouve que $r_1$ vaut :

Si on ajoute le fait que la dépression est remplie par un océan ou des sédiments, l'analyse reste la même : il suffit de rajouter un terme lors du calcul de la pression sous le bassin. Cela demande juste de connaitre la densité du matériel qui remplit la dépression, que l'on notera $d_e$. On obtient alors :

Mais attention : si ce modèle fonctionne pour les bassins, il ne fonctionne pas pour un rift ou une dorsale : la densité des matériaux n'est pas constante, une bonne partie des variations d'épaisseur étant causée par des différences de température.

Modèle de Pratt

Le modèle de Pratt a été inventé pour rendre compte d'une autre situation : celle d'une lithosphère de densité variable posée sur un manteau de densité uniforme. Dans ce modèle, la lithosphère est composée de blocs, comme dans le modèle de Airy. Encore une fois, les effets aux bords des blocs sont négligés, et l'équilibre isostatique local supposé valide.

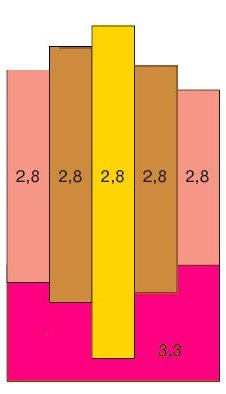
La différence avec le modèle d'Airy, c'est que chaque bloc a une densité différente. Ces blocs s’enfoncent tous à la même profondeur dans le manteau/l'asthénosphère : c'est leur altitude qui varie suivant la densité. Typiquement, les blocs les plus chauds se dilatent vers le haut, et ils ont donc une hauteur supérieure.

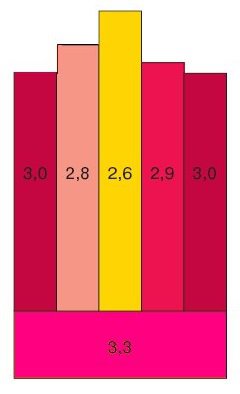
Le but du modèle de Pratt est de calculer la densité de la lithosphère, en connaissant sa hauteur.

Modèle de Pratt

Dans ce qui va suivre, l'épaisseur de la croûte normale est notée $e$, et sa densité $d_l$. Pour la lithosphère chauffée, elle aura une altitude de $h_1$, et une densité de $d_c$ (qui vaut entre 2,4 et 2,8 en situation réelle).

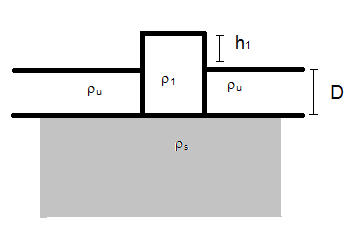
Sous une lithosphère normale, sans dilatation ou contraction thermique, la pression à la base est proportionnelle à $e \times d_l$. Sous la lithosphère chauffée, elle vaut $(h_1 + e) \times d_c$.

On se rappelle alors que la surface de compensation se situe à la base de la lithosphère ou de la croûte, vu que le manteau a une densité homogène.

En conséquence, les deux pressions calculées plus haut sont égales, ce qui donne :

On peut aussi étudier le cas de la subsidence thermique, dans laquelle la lithosphère s'amincit quand on la refroidit. Le traitement mathématique est alors similaire, mais fait appel à quelques hypothèses supplémentaires.

Validité empirique

Ce modèle modélise bien les situations où les variations d'épaisseur proviennent de variations de température du manteau, qui chauffe la lithosphère par en-dessous. Dans ces conditions, la lithosphère se dilate, ce qui a tendance à la bomber de quelques centaines de mètres de hauteur. Dans tous les cas, la plaque est très chaude au-dessus de la source de chaleur, mais elle refroidit en s'en éloignant.

Cela arrive sous certaines dorsales océaniques, riches en volcans, où les plaques s'écartent à une vitesse largement supérieures aux autres dorsales, et qui ont un rift central très limité (voire pas de rift du tout) : ces dorsales sont appelées des dorsales rapides. On trouve un équivalent continental de ces dorsales : les rifts actifs. Certains points chauds vont aussi chauffer les plaques qu'ils transpercent par en-dessous, et le modèle de Pratt est alors tout indiqué.

Dans la réalité, le bombement n'est pas totalement causé par l'augmentation de température de la croûte : la source de chaleur mantellique remonte vers la surface à cause de la poussée d’Archimède et appuie sous la lithosphère, ce qui crée un bombement supplémentaire. Mais le modèle de Pratt donne malgré tout de bons résultats.

Modèle de Vening-Meinez

Les deux modèles précédents ont toutefois un défaut : l'hypothèse d'équilibre isostatique local. Or, compte tenu du comportement des roches, cette hypothèse est irréaliste. La rigidité des plaques et celle du manteau font que la pression d'une chaîne de montagne va se répartir non seulement à la verticale, mais aussi sur les cotés, à l'horizontal. Ainsi, les racines d'une chaîne de montagne s'étalent, et les bassins sont légèrement surélevés sur les bords. L’équilibre isostatique local est brisé, et on parle plutôt d’équilibre isostatique régional.

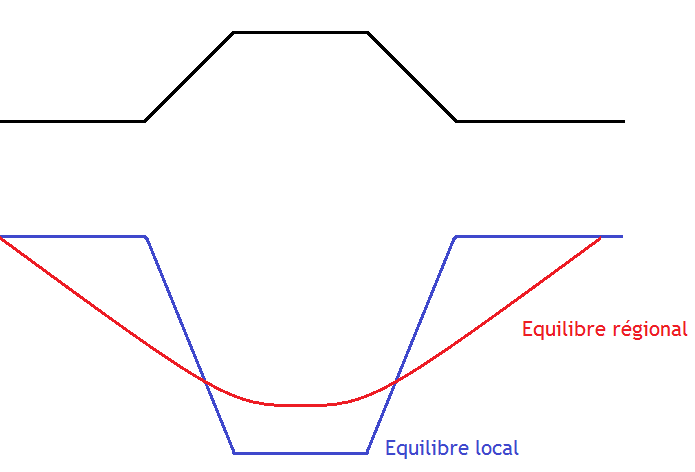
Il existe un modèle qui formalise l'effet de cette déformation de la lithosphère, qui s'appelle le modèle de Vening-Meinez. Dans ce modèle, la surface de compensation n'est pas forcément située à la base de la lithosphère ou de la croûte : elle peut se situer un peu plus bas, dans l'asthénosphère.

Les mouvements causés par l'isostasie

Il arrive que l'équilibre isostatique ne soit pas respecté : des mouvements tectoniques ou un changement dans l'épaisseur de la lithosphère peuvent rompre l'équilibre isostatique. La poussée isostatique se charge alors de ramener la lithosphère à l'équilibre, et des mouvements verticaux se mettent en place. Mais la lithosphère a une certaine viscosité, et met un certain temps avant de se remettre en place : les mouvements du manteau mettent un certain temps avant de faire remonter la lithosphère à l'équilibre isostatique. Il existe divers modèles qui permettent de tenir compte de cet effet (on parle de flexure de la lithosphère), et qui permettent de décrire précisément les exemples que je vais maintenant aborder.

Rebond glaciaire

Le cas le plus connu est celui du rebond post-glaciaire. Comme vous le savez peut-être, la Terre a subit des épisodes de glaciation plus ou moins prononcés, durant lesquels de grands glaciers se sont mis en place, notamment près des pôles. Ces glaciers recouvraient les continents sur plusieurs kilomètres, et formaient ce qu'on appelle un inlandsis.

Lors de la fonte de ces glaciers, au sortir de la glaciation, le continent s'est vu allégé du poids que lui imposaient les glaciers. Cette perte de masse a donc donné naissance à un rebond : la lithosphère est remontée de quelques centaines de mètres. Cette remontée ne s'est cependant pas faite brusquement, mais s'est étalée sur plusieurs millions d'années. Le relâchement de la pression des glaciers a été à l'origine de nombreux tremblements de terre, et d'une fracturation de la lithosphère.

L'exemple actuel le mieux connu est celui du nord du Canada, et du golfe de Botnie en Suède et Finlande. La remontée de la lithosphère se poursuit toujours dans le golfe de Botnie, à un rythme de 9 millimètres par an.

Sédimentation et érosion

La sédimentation a aussi un rôle à jouer sur l'isostasie. Quand beaucoup de sédiments s'accumulent à un endroit, la masse de ces sédiments pèse sur la lithosphère continentale ou océanique. On en trouve de nombreux exemples dans les bassins sédimentaires, des creux dans la lithosphère qui se remplissent de sédiments : le remplissage de ces cuvettes aggrave la descente et le creusement de la lithosphère.

Quand à l'érosion, elle permet de diminuer la charge posée sur la lithosphère : elle enlève de la masse. C'est ce qu'on observe dans les chaines de montagnes mortes, qui ne grandissent plus : l'érosion entraîne la remontée des roches profondes par isostasie. Pour remonter, ces roches doivent se plier, ce qui donne naissance à de nombreux plis.

Dans certains cas extrêmes, cela peut faire fondre ces roches. Il faut dire que les roches profondes, enfouies sous les chaines de montagnes sont soumises à des températures élevées. En remontant, elles gardent leur température, mais la pression baisse. La pression peut baisser suffisamment pour que la roche fonde, donnant naissance à un magma. De nombreux granites se forment de cette façon dans les chaines de montagnes érodées.

Poids d'une montagne ou d'un volcan

Comme dit plus haut, la naissance d'une montagne ou d'un volcan va rapidement épaissir la lithosphère. Cet épaississement peut être si rapide que la lithosphère n'est pas en équilibre isostatique : des mouvements verticaux sont alors à prévoir pour équilibrer le tout.

C'est le cas lorsqu'un volcan naît sur le fond de l'océan, notamment pour les volcans de point chaud. Dans ce cas, de grandes quantités de lave vont s'accumuler sur le plancher océanique, durant à peine quelques milliers d'années. Le volcan peut même émerger et donner naissance à une île, qui est alors colonisée par diverses espèces vivantes : le volcan peut notamment s'entourer d'une barrière de corail. Mais très vite, le volcan commence à s'enfoncer par isostasie. Le volcan finit par être immergé, mais la barrière de corail peut subsister à l'air libre : un atoll s'est formé.

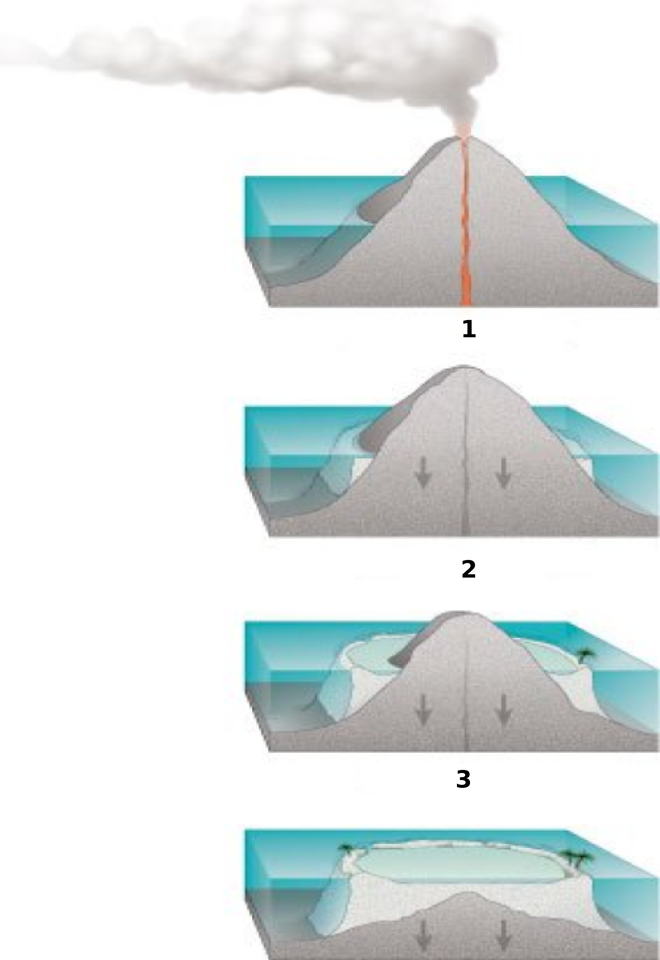
Variation du niveau des océans

Enfin, la variation du niveau des mers va aussi agir sur les continents. En effet, l'océan pèse sur le plateau continental et la croûte océanique, ce qui peut entraîner des mouvements isostatiques assez prononcés. Une simple augmentation de la quantité d'eau océanique, ou une variation de la superficie des océans est suffisante.

Refroidissement thermique

Et évidemment, le refroidissement de la lithosphère océanique qui s'éloigne d'une dorsale est un autre mécanisme de mouvements verticaux isostatiques, comme on l'a vu avec le modèle de Pratt.

Et voilà, vous savez maintenant ce qu'est l'isostasie, et quelles sont ses conséquences les plus connues.