TP : Inventons des équations !

Comme vous vous en doutez certainement, il y a énormément de réponses possibles. Une des plus simples que l’on puisse imaginer consiste à dire que 17 est le nombre qui donne 18 si on lui ajoute 1 :

$x+1=18$.

Et voici quelques unes des nombreuses autres réponses qui marchent.

• $x+2=19$ ;
• $x+3=20$ ;
• $x+1000000000=1000000017$ ;
• $x−17=0$ ;
• $x−117=−100$ ;
• $x\times2=34$ ;
• $10x=170$ ;
• $x\div 5=3,4$ ;
• $x\times 100+3=173$.

Bon, je m’arrête là, vous avez compris le principe. On pourrait en inventer autant qu’on veut sur le même principe.

Le principe est exactement le même pour inventer des équations dont la solution est 12345. En voici quelques unes :

• $x+1=12346$ ;
• $x\times 10=123450$ ;
• $x−11111=1234$ ;
• $x\div 100000=0,12345$.

Une fois que vous avez compris le fonctionnement, vous devez être capable d’inventer des équations dont la solution est n’importe quel nombre. Que ce nombre soit petit ou grand, positif ou négatif, avec ou sans chiffres après la virgule, tout ça n’y change rien, le principe reste le même.

On peut trouver une solution en retournant la question. Que faut-il faire au nombre 4,5 pour retomber sur un nombre entier ? le multiplier par 2 par exemple, ou bien par 10. Voici deux réponses possibles :

• $2x=9$ ;
• $10x=45$.

Bravo si vous avez trouvé une de ces deux équations ! Mais encore une fois, il y a de nombreuses autres réponses et si vous en avez trouvé une qui marche tout va bien.

Cette question est très similaire à la précédente. La seule contrainte supplémentaire est d’avoir le terme de droite de l’équation égal à 0, mais ceci ne doit pas vous faire peur si vous avez suivi le chapitre précédent, car vous savez que l’on peut passer les éléments d’une équation d’un côté à l’autre en inversant le signe.

Commençons donc par donner une équation sans division ni nombre à virgule dont la solution est 3,72, par exemple :

$100x=372.$ Il suffit maintenant de soustraire 372 des deux côtés pour obtenir :

$100x−372=0.$ Et c’est gagné ! Vous voyez, ce n’était pas si difficile que ça. Remarquez que là encore ce n’est pas la seule solution. Par exemple, vous pouvez remarquer que $25\times 3,72=93$, ce qui fait que l’équation suivante marche aussi :

$25x−93=0.$

Le fait que -2 et 2 soient opposés nous facilite la tâche. En effet, nous avons déjà vu dans le chapitre précédent que deux nombres opposés ont le même carré, l’équation que nous cherchons est donc :

$x^2=4.$ Et si vous voulez tout passer du même côté, on peut également réécrire cette équation de la façon suivante :

$x^2−4=0.$ Pour reprendre les schémas que nous avons utilisés dans le chapitre précédent, cette équation se représente de la façon suivante :

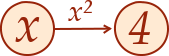
Et son schéma de résolution est le suivant :

Une fois que vous avez compris ceci, le fonctionnement est identique pour -7 et 7. On trouve l’équation suivante :

La question que nous devons nous poser est la suivante : que faut-il faire aux nombres -1 et 3 pour retomber sur -2 et 2 ? Facile : il suffit de leur soustraire 1. Autrement dit si on commence par soustraire 1 à $x$ pour obtenir $x−1$, il suffit ensuite d’appliquer à cette quantité les transformations de l’équation dont les solutions sont -2 et 2.

En clair, sur un schéma, les étapes s’enchaînent de la façon suivante :

L’équation correspondante est :

$(x−1)^2=4,$

ou bien $(x−1)^2−4=0$

si on fait passer le 4 à gauche. Voici alors le schéma de résolution de cette équation :

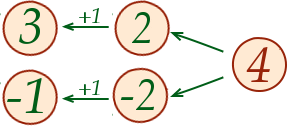
Vous constatez que tout se passe bien comme nous l’avions prévu : d’abord le carré donne -2 et 2, puis en remontant vers la solution on ajoute 1 ce qui donne bien -1 et 3. Astucieux n’est-ce pas ?

Pour appliquer le même raisonnement que pour la question précédente, il faut commencer par ajouter ou retrancher un nombre à -3 et 11 pour les rendre opposés l’un de l’autre. Avec un peu de réflexion, on se rend compte qu’il faut leur soustraire 4 : on obtient alors -7 et 7 qui sont solutions de l’équation $x^2−49=0$.

Au final, l’équation que nous cherchons est donc :

$(x−4)^2−49=0.$

Essayons maintenant d’expliquer plus généralement la méthode que nous utilisons pour être capables de la reproduire avec n’importe quels nombres. Pour mieux suivre ce qui se passe, appelons ces deux nombres $\alpha$ et $\beta$ et représentons les sur la droite des nombres réels de la façon suivante :

Il faut alors décaler ces deux nombres d’une certaine quantité de façon à obtenir deux nombres opposés. Le nombre qu’il faut soustraire est le nombre qui se situe juste au milieu de $\alpha$ et $\beta$, c’est-à-dire sa moyenne $(\alpha+\beta)/2$.

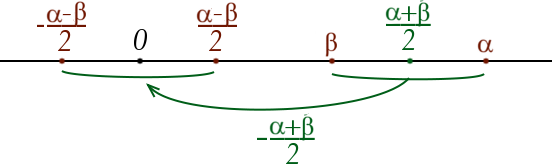
On voit que les deux nombres que l’on obtient se retrouvent à la distance $(\alpha−\beta)/2$ de chaque côté de 0, ce qui est logique puisque l’écart entre $\alpha$ et $\beta$ vaut $\alpha−\beta$ et n’a pas changé en retranchant la moyenne.

Les deux nombres obtenus étant opposés, on peut maintenant prendre le carré : ce sont les deux nombres dont le carré est égal à $[(\alpha−\beta)/2]^2$. En d’autres termes, l’équation que nous cherchons est la suivante :

$\left(x−\frac{\alpha+\beta}{2}\right)^2−\left(\frac{\alpha−\beta}{2}\right)^2=0.$ Vous pouvez remplacez $\alpha$ et $\beta$ par les nombres que vous voulez, ça marche toujours ! Nous venons de trouver une formule donnant une équation ayant pour solution n’importe quelle paire de nombres.

L’astuce est toute bête : il suffit de multiplier les deux équations :

$(x^3−2x^2−3x)\times(x^2+2x−35)=0.$ Si $x$ est égal à -1, 0 ou 3 alors la première des deux équations vaut 0 et donc le produit donne bien 0 aussi. Et si $x$ vaut -7 ou 5, alors c’est la deuxième équation qui vaut 0 et l’équation est également vérifiée.

Ce truc utilise simplement le fait que pour qu’une multiplication soit égale à 0, il faut et il suffit que l’un des termes multipliés soit égal à 0. Retenez bien cette astuce, car ce n’est pas qu’un simple gadget, c’est en réalité un des outils les plus puissants de la théorie des équations ! Nous nous en servirons à de nombreuses reprises dans la suite de ce cours.

Rien de vraiment nouveau dans cette question. Si vous avez bien compris ce que nous avons fait jusque là, il n’y a qu’à combiner les idées pour obtenir le résultat. Les dix petites équations ayant pour solutions les nombres de 1 à 10 sont par exemple :

• $x−1=0 ;$
• $x−2=0 ;$
• $x−3=0 ;$
• $x−4=0 ;$
• $x−5=0 ;$
• $x−6=0 ;$
• $x−7=0 ;$
• $x−8=0 ;$
• $x−9=0 ;$
• $x−10=0.$

Bien entendu, il y a d’autres possibilités que celles-ci, mais ce sont les plus simples. Notez qu’il faut toutefois bien faire passer tous les termes à gauche pour n’avoir plus que 0 à droite et pouvoir appliquer l’astuce de la question précédente.

Il n’y a plus qu’à tout multiplier pour obtenir la solution :

$(x−1)(x−2)(x−3)(x−4)(x−5)(x−6)(x−7)(x−8)(x−9)(x−10)=0.$ Pour que cette multiplication de dix termes soit égal à 0, il faut que l’une des parenthèse soit égale à 0, autrement dit que l’une des dix petites équations ci-dessus soit vérifiée. Ainsi cette équation a bien dix solutions qui sont 1, 2, 3, 4, 5, 6, 7, 8, 9 et 10.

Supposons que l’on veuille une équation dont les solutions sont -1, 0 et 3. Grâce au principe de la question précédente, c’est devenu facile, l’équation suivante fait l’affaire :

$(x−(−1))(x−0)(x−3)=0.$ Ce qui donne en simplifiant :

$(x+1)x(x−3)=0.$ Nous avons là affaire à une expression factorisée que nous pouvons développer : tout d’abord $(x+1)x=x^2+x$, et donc

$(x+1)x(x−3)=(x^2+x)(x−3)=x^3−3x^2+x^2−3x=x^3−2x^2−3x.$ Gagné, c’est bien l’équation qui était donnée dans la première question de cette section.

Pour la deuxième, ça marche pareil : l’équation est $(x+7)(x−5)$, ce qui en développant donne

$(x+7)(x−5)=x^2+7x−5x−35=x^2+2x−35.$

Considérons deux nombres $\alpha$ et $\beta$ et étudions les équations qui ont ces deux nombres pour solution. La méthode que nous venons de voir donne l’équation suivante :

$(x−\alpha)(x−\beta)=0.$ Pour supprimer les parenthèses, on peut développer cette expression :

$(x−\alpha)(x−\beta)=x^2−\alpha x−\beta x+\alpha\beta=x^2−(\alpha+\beta)x+\alpha \beta.$ Notre équation peut donc se réécrire de cette façon :

$x^2−(\alpha+\beta)x+\alpha \beta=0.$ Bien. Retenons cette équation et rappelons-nous maintenant de celle que nous avions trouvée dans la section précédente :

$\left(x−\frac{\alpha+\beta}{2}\right)^2−\left(\frac{\alpha−\beta}{2}\right)^2=0.$ Encore une fois, développons pour voir si nous trouvons la même chose. Pour développer les carrés, on utilise l’identité remarquable $(u+v)^2=u^2+2uv+v^2$.

$\begin{aligned}\left(x−\frac{α+β}{2}\right)^2−\left(\frac{α−β}{2}\right)^2&=\left(x^2−2x\frac{α+β}{2}+\left(\frac{α+β}{2}\right)^2\right)−\frac{α^2−2αβ+β^2}{4}\\ &=x^2−αx−βx+\frac{α^2+2αβ+β^2−α^2+2αβ−β^2}{4}\\&=x^2−αx−βx+\frac{4αβ}{4}\\&=x^2−(α+β)x+αβ.\end{aligned}$

Ouf ! Dans le fond ce n’est pas très compliqué mais il faut bien maîtriser la manipulation des fractions. J’espère que je ne vous ai pas perdu, le plus dur est fait !

Au final, notre équation développée est la suivante :

$x^2−(\alpha+\beta)x+\alpha\beta=0.$ Alors, que constatez vous ? Eh oui, le résultat est le même : une fois développées les deux équations que nous avions ayant pour solution $α$ et $β$ donnent le même résultat. Les deux équations sont donc bien les mêmes, mais juste présentées de façon différente. Étonnant, non ?