Dans un billet précédent, j’abordais la question de la modification d’une limite à cause de différents arrondis (pertes de précision).
Ce billet aborde la question duale : quelle précision faut-il avoir dans les calculs pour approcher la véritable limite à une distance donnée ?
- Rappel sur la convergence des suites arithmético-géométrique
- Précision des paramètres $a$ et $b$
- Précision des calculs
Rappel sur la convergence des suites arithmético-géométrique
Pour ceux qui n’auraient pas lu la première partie, voici un petit rappel sur les suites arithmético-géométriques.
Suite arithmético-géométrique
Une suite arithmético-géométrique est une suite définie par
où $a$, $b$ et $c$ sont des réels.
Nous allons éliminer les cas des suites purement arithmétiques ou purement géométriques, en supposant que $a \neq 1$ et $b \neq 0$.
Convergence
Avec nos hypothèses, il y a convergence si et seulement si $|a| < 1$, et la limite est, quelque soit la valeur initiale :
Précision des paramètres $a$ et $b$
Comment est affecté la limite par perturbation des paramètres ?
Perturbation sur $b$ seulement
Faisons subir une perturbation $\epsilon_b$ au paramètre $b$, ce qui modifie la limite en $u_\infty + \epsilon_u$ :
En résolvant cette équation pour $\epsilon_b$, on découvre que la limite est perturbée, bien sûr, en fonction de $\epsilon_b$, mais aussi de $a$.
La question de savoir quelle précision il faut sur $b$ pour limiter la perturbation sur $u_\infty$ trouve sa réponse dans l’équation suivante, facile à déduire :
Perturbation sur $a$ seulement
De manière analogue à précédemment, faisons subir une perturbation $\epsilon_a$ au paramètre $a$, ce qui modifie la limite en $u_\infty + \epsilon_u$ :
La question de savoir quelle précision il faut sur $a$ pour limiter la perturbation sur $u_\infty$ trouve sa réponse dans l’équation suivante :
Visualisation des perturbations en fonction de $a$ et $b$
Les équations précédentes montrent que les perturbations sur $a$ et $b$ qui engendrent une perturbation $\epsilon_u$ donnée dépendent de $a$ et $b$. Visualisons cela pour avoir quelque chose de plus concret à se mettre sous la dent.
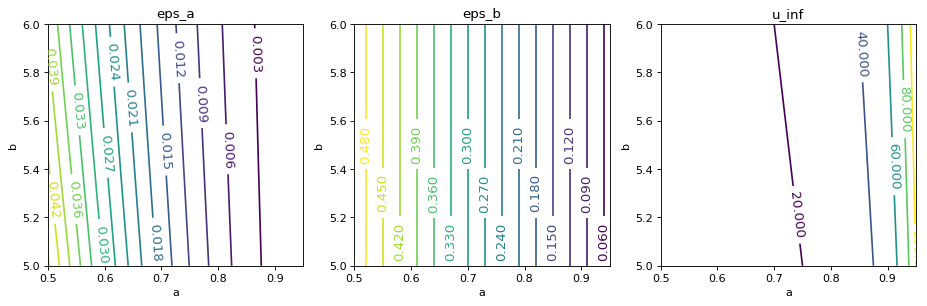
Ce genre de travail permet d’estimer la précision nécessaire sur $a$ et $b$ pour être précis à $\epsilon_u$ près sur la limite. Dans l’exemple de la figure, on trouve qu’il faut une précision de l’ordre de 10-4 sur $a$ et 10-2 sur $b$ pour que tout soit bon dans les intervalles que parcourent $a$ et $b$.
Perturbation simultanée de $a$ et $b$
Il n’y a, à première vue, pas de formule jolie pour relier $\epsilon_a$, $\epsilon_b$ et $\epsilon_u$ dans une seule formule. Il est possible dans le cas de petites perturbations de se partir sur des choses type différentielles, et de dire :
Précision des calculs
De manière plutôt intuitive, il faut une précision dans les calculs, notée $\epsilon$, qui soit plus faible que $\epsilon_u$. Mais de combien ?
Dans la suite, on considère $a$ et $b$ comme parfaitement connus.
Intervalle contenant les points fixes en fonction de $\epsilon$
Dans une suite récurrente convergente, les limites $u''_\infty$ obtenues pour différentes initialisations sont nécessairement des points fixes, de sorte qu’elles vérifient :
Je rappelle que $(\times)$ et $(+)$ sont les versions arrondies de $\times$ et $+$ respectivement.
Il s’agit maintenant de trouver à quelles conditions sur $u''_\infty$ on a effectivement cette égalité. Dans un premier temps, nous allons tenter de trouver une condition nécessaire.
Pour que $u''_\infty$ soit un point fixe, il faut que le résultat de l’addition non arrondie tombe dans le bon intervalle pour être arrondi vers $u''_\infty$. Autrement dit, il faut que :
Par équivalence, on a :
Comme pour l’addition, pour avoir ces inégalités, il faut que le résultat non arrondi de la multiplication tombe dans un intervalle qui est arrondi vers l’intervalle défini par l’inégalité ci-dessus. Cela correspond à :
Enfin, il est possible de transformer ce résultat en quelques étapes en :
En fin de compte, cela signifie que pour que $u''_\infty$ soit un point fixe, il doit être dans l’intervalle $[u_\infty - \frac{\epsilon}{1-a}, u_\infty + \frac{\epsilon}{1-a}]$.
Mais cela ne signifie pas qu’il suffit d’être dans l’intervalle : tous les points de l’intervalle ne sont pas des points fixes. Notamment, quelques essais rapides suggèrent que l’intervalle correspondant à l’ensemble des points fixes est aussi fonction de $b$ et semble dur à trouver analytiquement.
Valeur de $\epsilon$ pour obtenir une précision $\epsilon_u$ donnée
Maintenant qu’on sait donner un intervalle contenant tous les points fixes, il est possible de trouver quelle précision sur les calculs $\epsilon$ il faut choisir pour limiter l’erreur finale $\epsilon_u$.
Comme l’intervalle final à un rayon $\frac{\epsilon}{1-a}$, il suffit de prendre $\epsilon \leq \epsilon_u (1-a)$ pour avoir une erreur sur le calcul plus faible que $\epsilon_u$.
Exemple
On applique le résultat précédent pour les suites obtenues quand $a$ et $b$ parcourent $[0,55; 0,95]$ et $[5; 6]$ respectivement. Pour $\epsilon_u= 0,2$ et en faisant les calculs avec $\epsilon = \epsilon_u (1-a)$, on obtient les résultats ci-dessous concernant l’écart entre la vraie limite et la limite en précision limitée.

La figure est illisible, mais voilà ce qu’il faut retenir : le maximum sur la figure de droite est $0,199...$, tout juste en dessous de la valeur visée $\epsilon_u = 0,2$ !
La précision utilisée maximale sur cet intervalle est $\epsilon = 0,2 \times (1 - 0,95) = 0.01$, soit 20 fois plus précis que la précision souhaitée sur le résultat final. Cet écart augmente à mesure que $a$ se rapproche de 1.
Les résultats explorés dans cette série de billets sont certes basiques, mais peuvent déjà servir à justifier le design d’un estimateur embarqué, ce qui fera sûrement l’objet d’un prochain billet.