Pédagogie #2 : des schémas progressifs

Ce billet est le second de la série. Le premier est ici.

Cette série se veut illustrative. Il va de soi qu’elle ne se substitue en aucun cas à des études scientifiques.

Il semble préférable d’introduire progressivement au lecteur les éléments constituant un schéma plutôt que de fournir une visualisation touffue suivie de longues explications. Cela peut se faire en ajoutant effectivement les éléments au fur et à mesure ou en partant d’un schéma complet et en jouant sur l’opacité des composants.

Exemple : analyse de Sobol

Le contexte

En stage en R&D dans une startup dédiée à la simulation informatique, je travaille sur l’exploration de modèles. Ces derniers peuvent être vus comme des fonctions : on fournit des paramètres (par exemple, le taux d’intérêt appliqué par une banque) et le modèle nous retourne l’évolution d’une ou plusieurs mesures au cours du temps (par exemple, le profit fait par la banque). Explorer un modèle consiste à déterminer l’impact qu’ont les entrées sur les sorties (à la fois pour valider le modèle et assister la prise de décision).

Une méthode consiste à faire varier les arguments et de regarder à quel point cela fait varier les résultats. On parle d’analyse de Sobol (ou décomposition de variance). Une de mes récentes tâches consistait à illustrer à des personnes non statisticiennes l’usage d’une telle technique. Dans le document en question, je présente les résultats de l’analyse sous forme de graphes. Le lecteur a donc deux objets à comprendre :

Les concepts relatifs à la technique illustrée ;
Les visualisations utilisées pour rapporter les résultats.

Je me suis rendu compte que je pouvais rendre les explications plus accessibles avec des graphes plus progressifs. Voyez plutôt :

Version touffue

[…]

Nous utilisons la bibliothèque Python [SALib](https://salib.readthedocs.io/en/latest/) pour mener l’analyse. La procédure est la même que celle décrite dans l’exemple, à la différence près que notre modèle est stochastique, donc il nous faut aggréger les exécutions en une valeur :

Échantillonner l’espace des paramètres avec l’échantillonnage de Saltelli
Exécuter le modèle n fois avec chaque combinaison de paramètres
Pour chaque combinaison, aggréger les n exécutions en une seule valeur
Associer un nombre à chaque série temporelle produite (dernière valeur, min, max…) puis aggréger ces nombres (moyenne, écart-type…)
Ou aggréger toutes les séries en une seule (moyenne, écart-type…) puis résumer cette série en un nombre
Effectuer la décomposition de la variance

Le résultat contient trois types d’information pour chaque paramètre (ici p1, p2 and p3) :

Index d’ordre total (ST): tous les effets du paramètre
Index de premier ordre (S1): les effets du paramètre lorsqu’il varie seul
Index de second ordre (S2): les effets du paramètre lorsqu’il varie avec un autre paramètre seulement

Voici ce que nous obtenons en prenant la moyenne des dernières valeurs de chaque exécution :

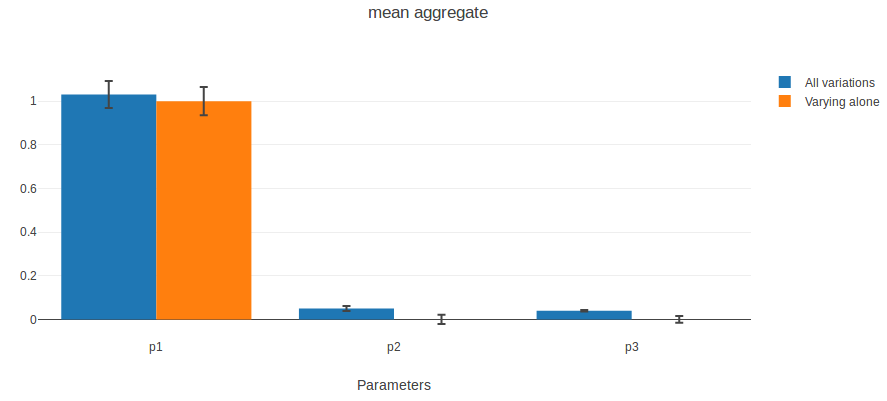
Les barres bleues représentent l’index d’ordre total. Les barres noires d’erreur correspondent à un interval de confiance à 95%.

Nous constatons que p1 est le paramètre influençant le plus la moyenne des dernières valeurs. Cela confirme ce que nous avons observé auparavant : p1 définit la tendance (qui définit la dernière valeur). The bruit introduit par p3 ne semble pas impacter la moyenne, donc la moyenne du bruit est la même pour toutes les valeurs de p3 et est nulle.

Les barres oranges représentent les index de premier ordre. La plupart des effets de p1 apparaissent quand il varie seul. p2 n’a pas d’effets de premier ordre, ce qui confirme ce que nous avons observé : la seule chose qu’il fait est d’interagir avec p1. Quand il varie seul, p3 n’a pas d’effet sur la moyenne non plus.

Version progressive

[…]

Échantillonner l’espace des paramètres avec l’échantillonnage de Saltelli
Exécuter le modèle n fois avec chaque combinaison de paramètres
Pour chaque combinaison, aggréger les n exécutions en une seule valeur
Associer un nombre à chaque série temporelle produite (dernière valeur, min, max…) puis aggréger ces nombres (moyenne, écart-type…)
Ou aggréger toutes les séries en une seule (moyenne, écart-type…) puis résumer cette série en un nombre
Effectuer la décomposition de la variance

Le résultat contient trois types d’information pour chaque paramètre (ici p1, p2 and p3) :

Index d’ordre total (ST): tous les effets du paramètre
Index de premier ordre (S1): les effets du paramètre lorsqu’il varie seul
Index de second ordre (S2): les effets du paramètre lorsqu’il varie avec un autre paramètre seulement

Voici ce que nous obtenons en prenant la moyenne des dernières valeurs de chaque exécution :

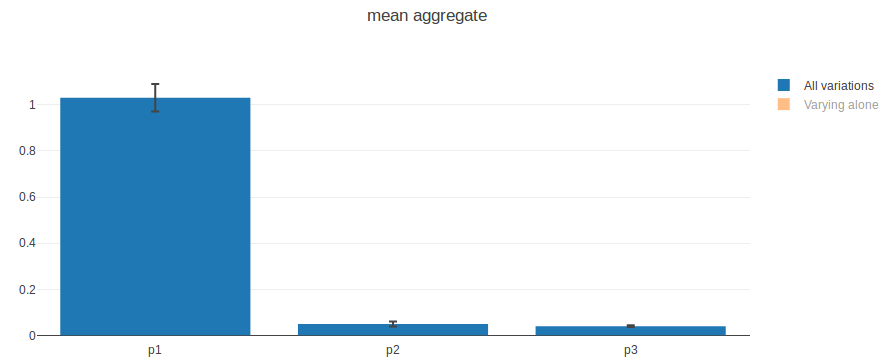
Les barres bleues représentent l’index d’ordre total. Les barres noires d’erreur correspondent à un interval de confiance à 95%.

Jetons un oeil aux index de premier ordre :

La plupart des effets de p1 apparaissent quand il varie seul. p2 n’a pas d’effets de premier ordre, ce qui confirme ce que nous avons observé : la seule chose qu’il fait est d’interagir avec p1. Quand il varie seul, p3 n’a pas d’effet sur la moyenne non plus.

Cohérence du schéma

La méthode présentée consiste à ajouter des éléments au fur et à mesure. Seulement, un schéma n’est pas toujours constitué de parties indépendantes qu’on peut cacher à sa guise et il est parfois nécessaire d’en afficher l’intégralité. Le cas échéant, on peut jouer sur l’opacité pour mettre en valeur les éléments un à un.

L’excellent article de Chris Olah¹ sur les cellules LSTM dans les réseaux de neurones récurrents illustre cela très bien. Il n’est pas nécessaire de connaître ces notions pour apprécier la pédagogie de l’auteur.

On commence avec une vue d’ensemble :

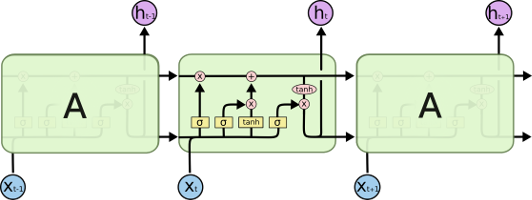
Cela permet au lecteur de reconnaître des éléments familiers et de se poser des questions. Puis on introduit un élément…

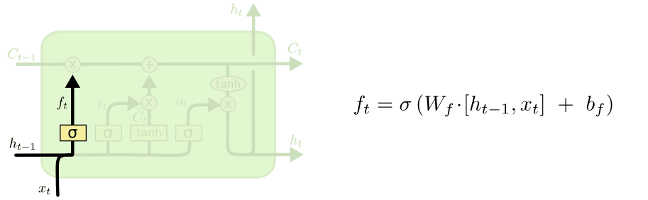
… qu’on décrit. Et recommence avec un second :

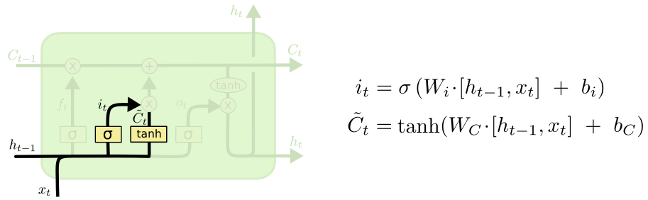
Également analysé. Etc.

Un schéma ou plusieurs ?

Quand les éléments sont relativement indépendants (comme dans le premier exemple), on peut se demander quel est l’intérêt de les faire apparaître sur le même schéma. En voici quelques uns :

L’interaction des éléments peut aider à la compréhension (dans le cas de l’analyse de Sobol, on peut mettre en perspective les indices de premier ordre avec ceux d’ordre total) ;
Faire apparaître les éléments précédemment décrits fait office de répétition (visuelle en l’occurrence), bénéfique à la mémorisation ;
Ce faisant, on obtient à la fin un schéma récapitulatif très pratique pour résumer le cheminement suivi dans le contenu.

Tous ses articles sont des perles. ↩