- Yuri's Night : le Café des Sciences passe en direct pendant le confinement
- Modéliser la propagation du SARS-CoV-2
Aujourd’hui j’aimerais vous présenter une technique qui permet de simplement modéliser un système optique sans recourir aux traditionnelles formules de conjugaison que l’on apprend au lycée. Cette technique a l’avantage d’être relativement simple et c’est pourquoi je vais tenter de l’introduire dans ce billet !
Ce contenu est une version légèrement retravaillé de ce post de blog.
- Rappels de mathématiques
- Comment étudier la lumière ?
- Multiplications dans tous les sens
- Matrices optique
Rappels de mathématiques
Dans la suite nous allons avoir besoin de faire des calculs avec des matrices. Pas de panique, pas de prérequis compliqués je vais tout expliquer simplement. Les vrais matheux sont priés de m’envoyer un mail pour que l’on organise ma pendaison publique.
Nous n’allons utiliser que des matrices . Qu’est-ce que donc que cela ? tout simplement un objet mathématique avec 4 dimension. C’est à dire que l’on définit avec quatre nombres. Par exemple si notre matrice est définie avec les nombres , , et , nous l’écrirons
Dans la suite nous auront également besoin de vecteurs. Là encore il s’agit d’un objet mathématique particulier. Un vecteur se caractérise par deux grandeurs. Ainsi par exemple, si l’on a un vecteur défini par les grandeurs et , on le notera
Opérations sur nos jouets : l’addition
Avec nos nouveaux jouets, nous allons pouvoir réaliser quelques opérations. Dans la suite, nous utiliserons deux matrices, et , et un vecteur que nous noterons comme suit :
Dans cette partie, nous allons voir deux façons de combiner et . La première est de les additionner. Le résultat de l’addition de deux matrices s’écrit
Rien de bien compliqué non ? la somme de deux matrices est une matrice dont les composantes sont les sommes des composantes des matrices.
Opérations sur nos jouets : multiplication par un scalaire
De même, on peut multiplier une matrice ou un vecteur par un scalaire. Soit un scalaire,
Le produit d’un scalaire et d’une matrice est une matrice dont les composantes sont le produit du scalaire et des composantes de la matrice. Pareillement, le produit d’un scalaire et d’un vecteur est un vecteur dont les composantes sont le produit du scalaire et des composantes du vecteur
Nous verrons d’autres opérations réalisables sur ces objets, mais nous n’en avons pas besoin pour l’instant.
Comment étudier la lumière ?
Il existe beaucoup de modèles de la lumière, que ce soit corpusculaire ou ondulatoire. La question de sa nature a donné l’occasion à beaucoup de scientifiques de s’arracher des cheveux. Quel est donc le bon modèle à utiliser ? la réponse est… que cela n’a pas d’importance dans notre cas. L’optique géométrique reste valide dans beaucoup de cas, en particulier pour ce qui concerne des dispositifs tels que les microscopes, les téléscopes, les loupes… C’est aussi une façon d’aborder l’étude de la lumière simple qui permet parfois une première approche à certains systèmes complexes. Enfin, l’optique géométrique ne permet pas d’expliquer des phénomènes tels que la diffraction ou les interférences.
Nous allons étudier la propagation de la lumière dans un plan, dans une direction donnée. On utilisera un repère orthonormé . Pour matérialiser le comportement de la lumière, on utilise le concept de rayons lumineux. Si vous imaginez la lumière comme étant de minuscules billes se déplaçant dans l’espace, alors ces rayons peuvent être vus comme des trajectoires. Nous faisons l’hypothèse que, sans interaction, la lumière se déplace en ligne droite. Autrement dit, si l’on trace un rayon lumineux dans le vide, il s’agit d’une droite. On peut donc représenter sa trajectoire comme sur l’image suivante :
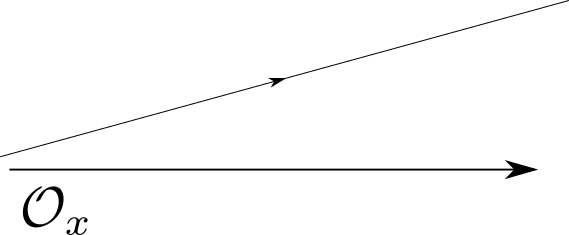
On indique l’axe (que l’on appelle l'axe optique) pour se donner une idée de la direction de propagation du rayon, et on donne le sens grâce à la petite flêche sur le rayon. En se plaçant à l’endroit sur l’axe d’où est émis ce rayon, on peut donc caractériser cette demi-droite par deux informations : la hauteur et l’angle avec l’horizontale .

On représente un le rayon avec le vecteur suivant :
Toute la suite de cet article aura pour but de travailler sur ce vecteur afin de trouver comment il évolue. Pour cela, nous allons avoir besoin d’un nouvel interlude mathématique…
Multiplications dans tous les sens
Pour l’instant, nous ne savons qu’additionner des matrices et multiplier par un scalaire un vecteur ou une matrice. Il temps que cela change !
Multiplication d’une matrice et d’un vecteur
Nous allons définir la multiplication à gauche d’un vecteur par une matrice. Attention, ici, le sens de la multiplication est important. On parle bien de la multiplication . On la défini ainsi :
Le produit d’une matrice et d’un vecteur est un vecteur dont les composantes sont la combinaison de la première ligne de la matrice avec les composantes du vecteur et la combinaison de la deuxième ligne de la matrice avec les composante du vecteur.
Multiplication de deux matrices
On peut également multiplier deux matrices carrées (je rappelle que les matrices qui nous intéressent sont carrées). Ainsi,
On peut remarquer que le résultat est similaire à celui obtenu lors de la multiplication , si l’on considère que la matrice comme un couple de vecteurs : .
Cette formule peut sembler un peu pénible à retenir. À titre personnel, je la retrouve à l’aide d’une petite astuce que j’ai tenté de résumer dans l’animation suivante :
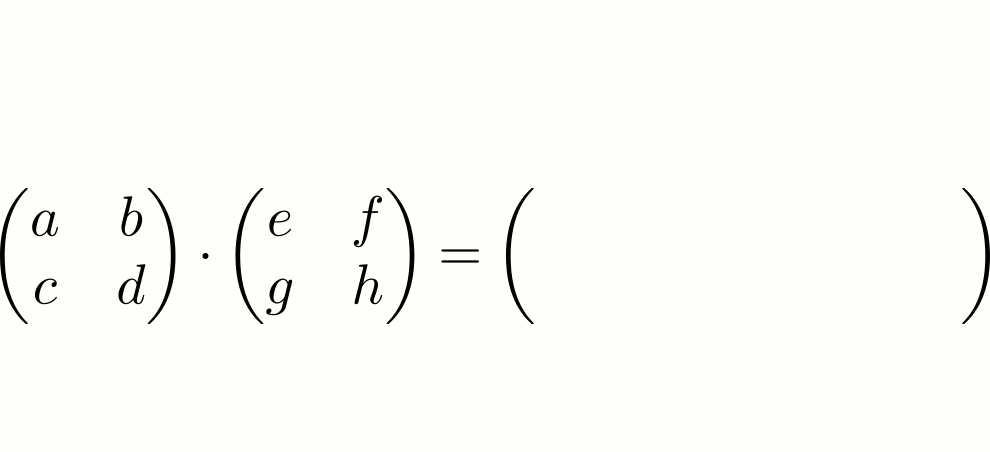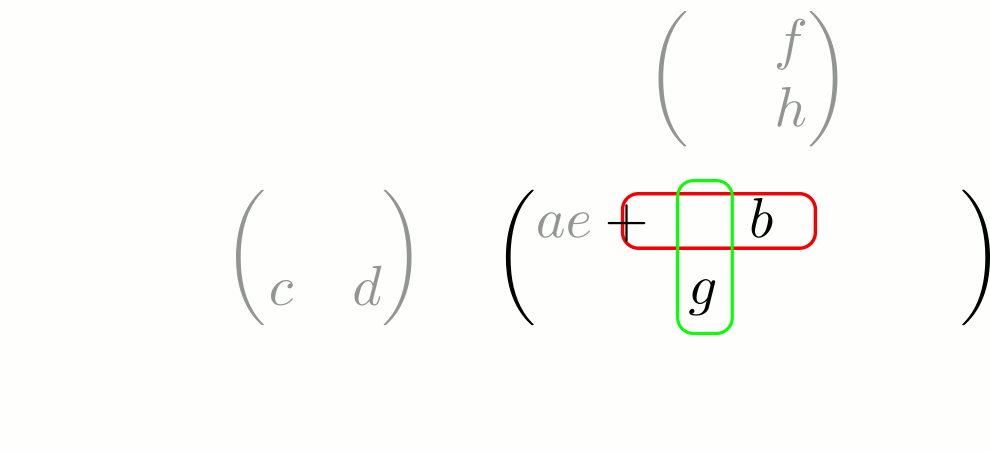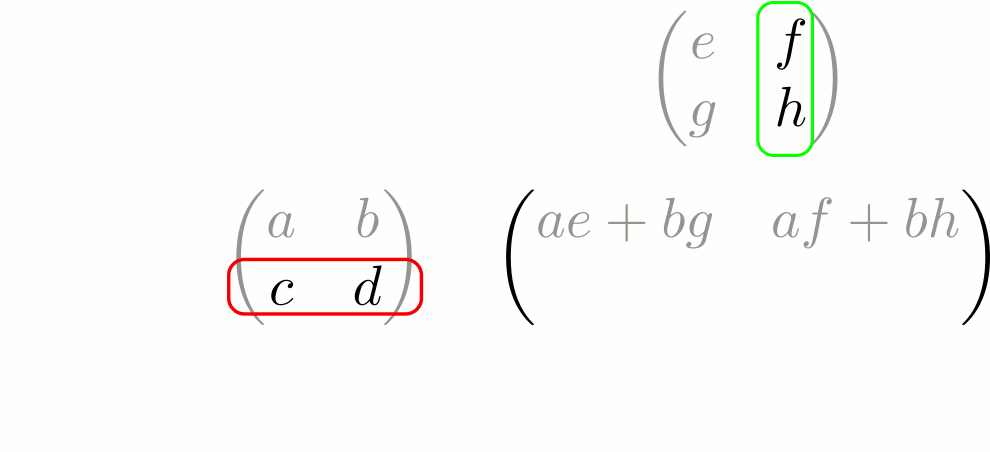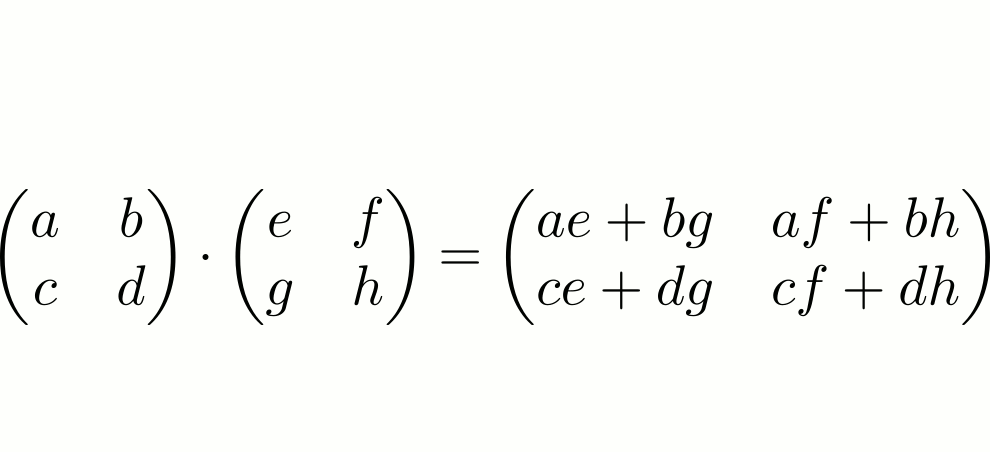
Matrices optique
Grâce au produit matriciel, nous allons pouvoir exprimer les transformations que subit le vecteur représentant la lumière lorsque cette dernière se propage. L’idée principale est de déduire une matrice telle que, si l’on connaît le vecteur originel , on puisse déduire le vecteur d’arrivée tel que .
Propagation dans un matériau
Supposons que l’on souhaite connaître l’évolution de notre vecteur après propagation dans un matériau sur une longueur .

On a alors
Comme on se place dans l’approximation des petits angles, on a alors
Si on pose le vecteur originel et le vecteur après propagation, tels que on a :
Cette expression va nous permettre de déduire une matrice telle que :
On remarque que l’angle de propagation ne varie pas lorsque le rayon se propage dans le vide, ce qui est conforme à notre dessin. Il est temps de trouver des matrices plus amusantes.
Loi de Snell-Descartes et interfaces entre milieux
Jusqu’à maintenant j’ai, dans le but de simplifier, supposé que la lumière se propageait dans le vide. Mais afin de pouvoir altérer son angle de propagation, il est utile de lui faire changer de milieu. Pour rappel, en optique géométrique, on caractérise un milieu par son indice, noté . Ainsi, si l’on considère l’interface entre deux milieux d’indices et , un rayon qui se propage en direction de cette interface se verra en partie réfléchi, et en partie transmis (on parle de réfraction).

Comme le laisse deviner mon schéma, la partie réfléchie le sera de l’autre côté de la normale avec le même angle que celui d’arrivée. L’autre partie sera transmise avec un angle qui vérifie la relation de Snell-Descartes :
Nous voulons exprimer la relation entre le vecteur du rayon avant l’interface et le vecteur après l’interface. Dans l’approximation des petits angles, la relation de Snell-Descartes s’écrit La position du rayon ne changeant pas, la composante de est la même que celle de . On a alors
On peut donc en déduire la matrice :
Exercice : combinaison de propagations
Avec les deux matrices que nous avons vu, nous pouvons déjà réaliser un premier exercice !
On dispose d’un objet plongé dans l’eau d’où partent deux rayons et . Le but est de calculer et , les vecteurs rayons qui résultent de leur propagation.
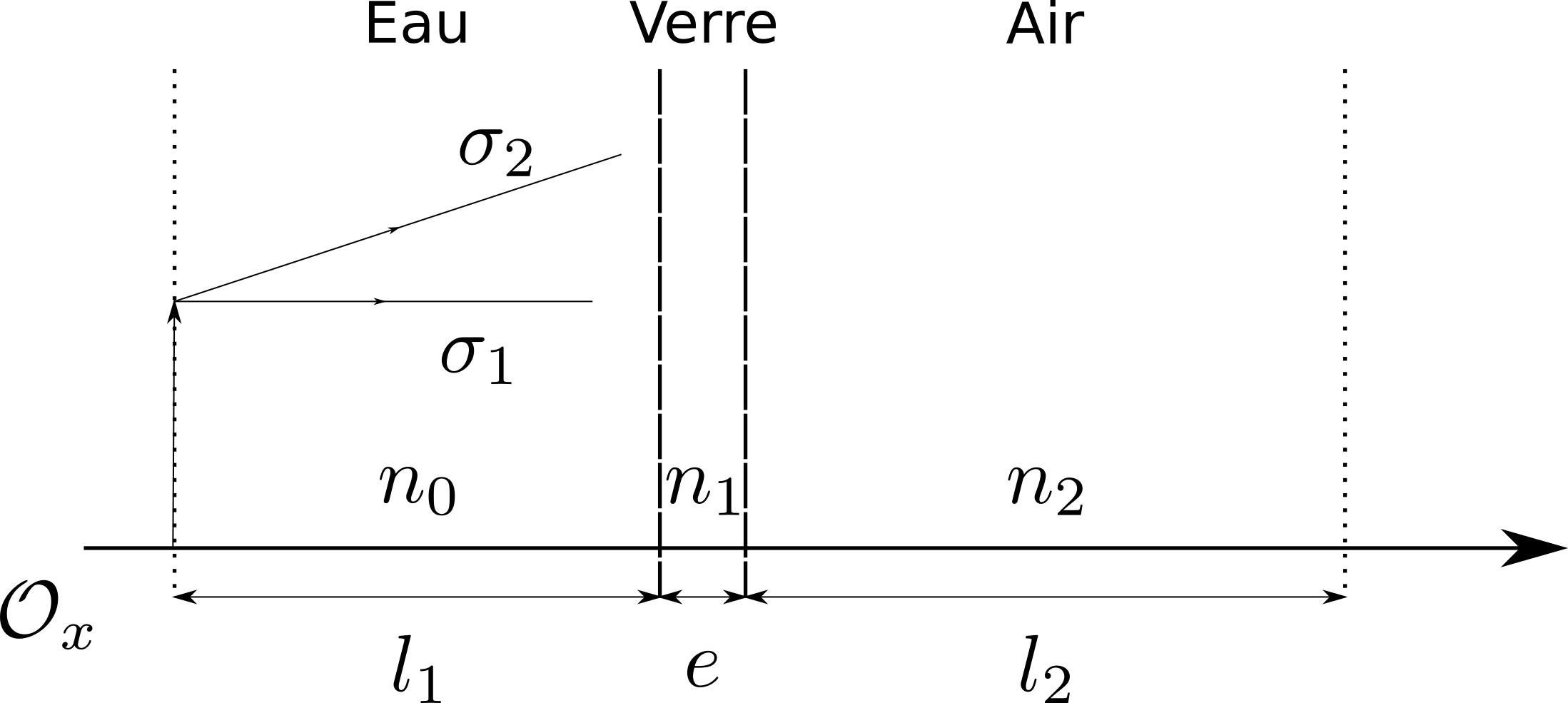
On pose
Données :
| Grandeur | Valeur | Unité |
|---|---|---|
| cm | ||
| cm | ||
| mm | ||
| cm | ||
| rad | ||
| rad |
À vos stylos ! il est interdit de regarder la correction sans avoir essayé.
Correction
La première étape est de déterminer quelles matrices nous allons calculer. On peut découper la propagation en 5 étapes:
- Propagation dans l’eau;
- Interface eau-verre;
- Propagation dans le verre;
- Propagation dans l’air.
Appelons , et les matrices de propagation dans l’eau, dans le verre et dans l’air. Appelons la matrice représentant l’interface eau-verre et la matrice représentant l’interface verre-air.
On peut donner directement les expressions des matrices :
On pourrait calculer étape par étape tous les vecteurs rayons, mais ce n’est pas nécessaire. En effet, on peut remarquer que pour un rayon représenté par un vecteur , les vecteurs engendrés sont
- ;
- ;
- ;
- ;
- ;
En "dépliant" le tout, on remarque qu’il suffit donc de calculer la matrice telle que
Pour éviter de se fatiguer à tout calculer, on peut ici utiliser un logiciel de calcul formel comme wolfram alpha. On obtient alors :
On peut remarquer que, à condition que soit faible devant , on a
C’est à dire que si l’on a un verre suffisamment fin, on peut ne considérer qu’une interface eau-air.
Pour finir, on peut calculer les vecteurs d’arrivée. Pour cela j’ai réalisé un petit script en Julia:
l_1 = 10 # cm
l_2 = 40 # cm
e = 3.0e-1 # cm
n_0 = 1.3
n_1 = 1.5
n_2 = 1.0
y = 5.0 # cm
θ_1 = 0 # rd
θ_2 = 1.7e-1 #rd
P_0 = [1 l_1; 0 1]
P_1 = [1 e; 0 1]
P_2 = [1 l_2; 0 1]
M_ev = [1 0; 0 n_0/n_1]
M_va = [1 0; 0 n_1/n_2]
M = P_2 * M_va * P_1 * M_ev * P_0
σ_1 = [y; θ_1]
σ_2 = [y; θ_2]
(M*σ_1, M*σ_2)
Ce qui nous donne : ([5.0, 0.0], [15.5842, 0.221]). Comme on pouvait s’y attendre, le rayon qui part perpendiculairement aux interfaces n’est pas dévié. On peut calculer la valeur qu’aurait prise le vecteur si la propagation s’était faite sans changement de matériau :
julia> [1 l_1+l_2+e; 0 1]*σ_2
2-element Array{Float64,1}:
13.551
0.17
On voit que le rayon se serait trouvé plus bas. Inversement, pour obtenir un rayon arrivant à 15.5842 cm de haut, il aurait fallu que la source se trouve plus loin. Autrement dit, pour un observateur extérieur, la source semble plus éloignée que ce qu’elle est réellement.
Hop hop hop, on m’avait parlé d’une technique pour ne pas utiliser les formules de conjugaison ! On y a même pas fait allusion, et je ne saurais pas résoudre un exercice type avec des lentilles avec ça !
Bonne remarque. Mais ce billet est déjà relativement long. Avec ceci vous disposez de tout le matériel nécessaire. Dans un prochain billet, on pourra approcher d’autres systèmes et voir des vrais cas pratiques !