Dans le deuxième article de cette série, nous avons vu comment implémenter une simili multiplication pour les flottants. Cette approximation nous permettait de gagner quelques microsecondes par multiplication, et avait également l’avantage d’avoir un coût d’utilisation constant.
Pour la comparaison, j’ai donné les temps nécessaires pour multiplier deux entiers long de 32 bits.
Notre petite mesure donnait 5,75 µ s pour la multiplication entière, contre
7,1875µ s pour la multiplication flottante. La différence étant encore plus
flagrante pour l’addition. Nous avions expliqué cela par la nécessité pour le
compilateur d’émuler une FPU (Floating Point Unit) afin d’être en mesure de
réaliser les opérations sur les flottants. La conclusion que nous en avions tirée
était qu’il fallait parfois mieux ne pas utiliser ces flottants, et les
remplacer par des nombres en virgule fixe. C’est tout l’objet de ce troisième et
dernier article de la série!
Ce billet a été initialement rédigé pour la newsleter FedeRez de Juillet 2022 (non disponible publiquement à ma connaissance).
Présentation et notations.
C’est fixé, nous souhaitons réaliser nos opérations sur des entiers plutôt que sur des flottants. Du moins, on souhaite que le processeur travaille avec nos nombres comme il travaillerait avec des entiers. Une solution est donc de lui donner des entiers, mais de considérer que la virgule se situe quelque part entre deux des bits du nombre plutôt que tout à droite.
Pour l’exemple, supposons que l’un des registres du processeur stocke l’octet 01000001.
L’interprétation de ce nombre , s’il s’agissait d’un entier signé, serait
. À présent, supposons qu’un drôle de
personnage (vous par exemple), décide de placer la virgule entre les deux bits
les plus à gauche, on aurait donc
Naturellement, pour chaque position où l’on peut mettre une virgule, on peut définir un format de nombre à virgule fixe. C’est pourquoi il est nécessaire de choisir une notation. Pour ma part, j’utiliserai dans la suite de cet article le format utilisé dans la documentation de Microchip. Dans l’exemple précédent, le choix de placement de la virgule serait noté : on a un un bit pour les unités (ou le signe) et sept pour la partie fractionnaire. Si le nombre est négatif, on procède comme pour un entier: on stocke en mémoire son complément à deux. Cela nous permet de réaliser les additions de manière transparente (comme si nous avions des entiers) et la multiplication n’est guère plus compliquée.
Notre fil rouge.
L’addition pouvant se faire sans contrainte particulière, c’est-à-dire avec exactement les mêmes instructions que l’addition des entiers, nous allons nous pencher sur la multiplication, notre fil rouge, mais cette fois avec des nombres en virgule fixe.
Avant de nous jeter sur l’implémentation, vérifions que nous savons faire des multiplications de nombres entiers (oui, oui, comme à l’école primaire). Prenons par exemple les deux nombres et . Puisque ces deux nombres sont représentés sur quatre bits, le résultat s’écrira sur au plus huit bits1 Si l’on pose la multiplication, on a :
Jusqu’ici tout cela est probablement trivial. Il est néanmoins intéressant de se poser la question de comment gérer les nombres négatifs. Comme vous l’avez remarqué, j’ai complété avec des zéros les deux opérandes de la multiplication pour travailler tout de suite avec le nombre de bits du résultat. Dans le cas d’un nombre négatif (c’est à dire quand le bit le plus à gauche est à un), il faudra à l’inverse compléter avec des uns2. Choisissons par exemple de prendre en première opérande l’opposé de celle du premier exemple: .
J’ai certes choisi des exemples triviaux, mais je vous fais confiance pour vous entraîner avec des exemples compliqués qui font apparaître des retenues. Le point important est que le résultat tient sur 8bits, on n’interprète pas d’éventuelles retenues qui se propagent plus loin.
- Vous pouvez vérifier cela en regardant le résultat de par lui même: on obtient . De manière générale, en multipliant deux nombres sur bits, le résultat tient sur bits.↩
- Si cela vous semble louche, vous pouvez essayer de représenter sur huit bits l’opposé d’un nombre négatif, puis calculer son complément à deux. Vous constaterez que vous obtenez le même résultat que si vous «complétez» le nombre sur quatre bits avec des uns.↩
Et les nombres à virgule fixe?
Comme je l’ai dit avant, on les choisit parce qu’ils se comportent comme des nombres entiers, la multiplication se déroule donc comme décrite précédemment. La seule subtilité se trouve dans l’interprétation du résultat. En effet, nous avons vu que le résultat de la multiplication de deux entiers de taille tient sur un entier de taille .
Mais dans le cas de nombres en virgule fixe, où placer la virgule du résultat ? On peut partir de ce que l’on sait déjà pour les nombres entiers: la multiplication de deux nombres sur bits donne un résultat sur bits. On doit garder cette propriété pour la partie entière des nombres à virgule fixe. Pour la partie fractionnaire (celle après la virgule) on peut appliquer le même raisonnement : le plus petit nombre (en valeur absolue) obtenu après la multiplication de deux nombres au format est le résultat de la multiplication du plus petit nombre de ce format par lui-même. Ce plus petit nombre étant , le résultat peut aller jusqu’à . Au final, notre résultat peut donc être représenté par le format .
Pour être certain de ne pas vous avoir perdus, reprenons notre exemple précédent, mais en considérant qu’il s’agit d’une représentation . En choisissant et , on a toujours le même résultat de la multiplication posée : (vous pouvez vérifier, le résultat est exact).
Mise en pratique.
Il existe plusieurs bibliothèques qui permettent d’utiliser les nombres à virgule fixe. En particulier, sur Arduino et apparentés, FixedPointsArduino fait du très bon travail, avec une simplicité d’utilisation remarquable grâce aux templates C++.
Mais pour pimenter un peu les choses, je vous propose d’essayer de
construire une implémentation qui tire parti des instructions spécifiques à la
famille des processeurs AVR dont l’ATMega328P de l’Arduino fait partie. En
particulier, ce processeur dispose de trois instructions permettant la
multiplication en virgule fixe de nombres sur un octet : fmul, fmuls et
fmulsu. Ces trois instructions réalisent respectivement la multiplication de
deux nombres non signés, de deux nombres signés et d’un nombre signé par un
nombre non signé.
Pourquoi parler d’une multiplication en virgule fixe alors que j’ai passé la
section précédente à répéter qu’il s’agit de la même multiplication que pour les
entiers ? Il s’agit simplement d’un problème de stabilité de format. En effet,
si on multiplie « comme des entiers » deux nombres au format , le résultat obtenu
doit être un entier sur deux octets au format . Si on conserve le résultat
sous ce format, une nouvelle multiplication nécessitera un résultat au format
. On comprend vite qu’il faut adopter une stratégie pour limiter cet effet. Le
plus simple est de formater le résultat de l’opération pour obtenir un nombre au
format , quitte à obtenir un résultat faux. Pour cela, les instructions
fmul et associées réalisent un décalage à gauche du résultat, de telle manière
que le résultat final de l’opération est au format , et le bit de retenue
du registre de status est mis à un en cas de débordement.1 Pour
obtenir un résultat au format il suffit alors de ne récupérer que le
premier octet du résultat.
2: Vous pouvez vérifier cela en regardant le résultat de
par lui même: on obtient . De manière générale,
en multipliant deux nombres sur bits, le résultat tient sur bits.
En utilisant ces trois opérations de multiplication en virgule fixe, il est
possible d’écrire une multiplication pour les nombres au format .
L’instruction fmuls se charge de la multiplication des octets les plus
significatifs, fmul des octets les moins significatifs, et fmulsu des deux
produits croisés.
Il faut ici faire attention à la retenue des produits croisés: puisque le résultat est signé, s’il y a une retenue, alors le résultat est
négatif et il faut soustraire cette retenue (et non l’ajouter comme on pourrait
penser de prime abord) de l’octet suivant.
En sachant cela, on peut écrire une petite fonction qui multiplie de manière efficace des nombres à virgule fixe sur deux octets. Le code assembleur est principalement repris de la documentation des instruction AVR
typedef uint16_t sFixed;
sFixed fixed_mul(sFixed a, sFixed b) {
sFixed result;
asm (
// We need a register that's always zero
"clr r2" "\n\t"
// Multiply the MSBs
"fmuls %B[a],%B[b]" "\n\t"
"movw %A[result],__tmp_reg__" "\n\t"
// Multiply the LSBs
"fmul %A[a],%A[b]" "\n\t"
// Do not forget the carry
"adc %A[result],r2" "\n\t"
// LSBs multipliplication is stored in
// temporary registers
"movw r18,__tmp_reg__" "\n\t"
// First cross product
"fmulsu %B[a],%A[b]" "\n\t"
// This will be added to MSBs of the
// temporary registers and the LSBs of
// the result registers. So the carry
// goes to the result's MSB.
"sbc %B[result],r2" "\n\t"
// Now we sum the cross product
"add r19,__tmp_reg__" "\n\t"
"adc %A[result],__zero_reg__" "\n\t"
"adc %B[result],r2" "\n\t"
// Second cross product, same as first.
"fmulsu %B[b],%A[a]" "\n\t"
"sbc %B[result],r2" "\n\t"
"add r19,__tmp_reg__" "\n\t"
"adc %A[result],__zero_reg__" "\n\t"
"adc %B[result],r2" "\n\t"
"clr __zero_reg__" "\n\t"
:
[result]"+r"(result):
[a]"a"(a),[b]"a"(b):
"r2","r18","r19"
);
return result;
}
On peut enfin essayer de comparer le temps d’exécution avec d’autres
implémentation pour savoir si nos efforts ont payé. Dans la figure suivante,
j’ai comparé les temps d’exécution de la fonction précédente avec son équivalent
dans la bibliothèque FixedPointsArduino. Pour
compléter, j’ai aussi ajouté les multiplications sur 8 bits (la version
assembleur se contente d’appeler l’instruction fmuls) et quelques
multiplications flottantes. Les différents codes conçus pour cette mesure sont à
retrouver ici.
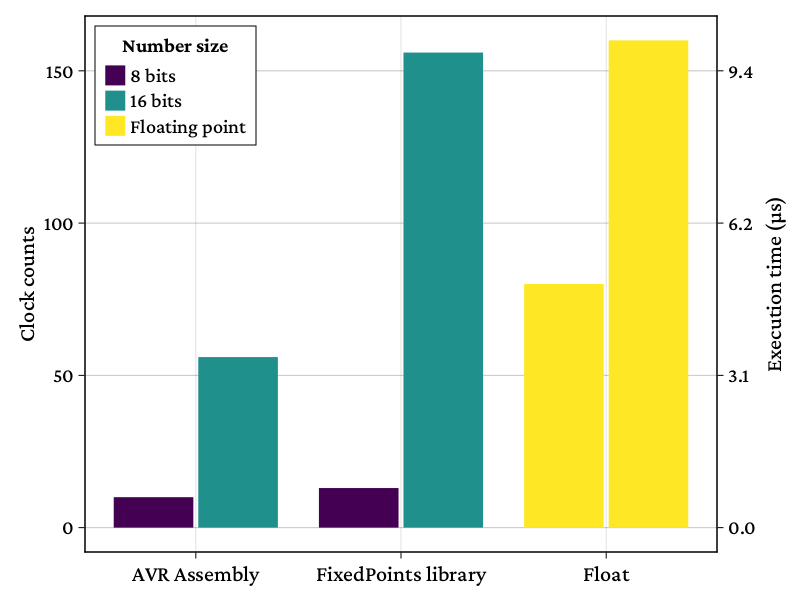
On voit que notre plongée dans les spécificités de la représentation en virgule fixe nous aura permis de gagner de précieuses microsecondes sur la multiplication. De plus, on conserve les très bonnes propriétés d’additions des entiers (par comparaison à celle des flottants). Pour des calculs où la plage de valeurs prises par nos variables ne change pas, la représentation en virgule fixe semble donc bien adaptée!
J’espère qu’avec cette série d’articles, vous aurez pu profiter d’un petit tour sympathique (quoique peut-être un peu centré sur les microcontrôleurs AVR) de la représentation de variables non entières, et que cela vous donnera envie de bidouiller un peu plus le sujet!
 En période de canicule, une idée fixe: économiser la float
En période de canicule, une idée fixe: économiser la float