Programme de calcul de vol d'une fusée

Bonjour,

Nous avons eu en classe un TP dans lequel nous devions réaliser le calcul de vol d’une fusée en phase de montée en Python. On nous a donnée le système différentiel suivant :

Avec les données suivantes :

• $D = 4\ kg.s^{-1}$, le débit massique des gaz
• $a_0 = 8.10^3\ m$
• $g = 9.81\ m.s^{-2}$
• $k_0 = 0.1\ N.m^{-2}s^2$,
• $u = 2.10³\ m.s^{-1}$
• $v$, la vitesse, initialement à $0\ m.s^{-1}$
• $m$ la masse initialement à $400\ kg$ et à $80\ kg$ à la fin de la combustion
• $z$ l’altitude, initialement à $0\ m$

Je souhaiterais également réaliser la phase de descente de la fusée, il faut donc modifier notre système différentiel (notamment supprimer la poussée). J’ai réalisé le code suivant :

from scipy.integrate import odeint
import matplotlib.pyplot as plt
import math


D = 4
g = 9.81
a0 = 8e3
k0 = 0.1
u = 2e3

# Y[0] => vitesse : v
# Y[1] => masse : m
# Y[2] => altitude : z


def subdivise(a, b, N):
   return [a + k * ((b - a) / (N - 1)) for k in range(N)]


def compute_dv(Y, t):
   if Y[1] > 80:  # Si la masse est supérieure à 80
       dv = ((D * u) / Y[1]) - g - k0 * math.exp(-(Y[2] / a0)) * (Y[0] ** 2 / Y[1])
       dm = -D
       dz = Y[0]
   else:
       dv = -g - k0 * math.exp(-(Y[2] / a0)) * (Y[0] ** 2 / Y[1])
       dm = 0
       dz = Y[0]
   
   if Y[2] < 0:  # Si l'altitude est inférieure à 0
       dv = 0
       dz = 0
       dm = 0

   return dv, dm, dz


if __name__ == "__main__":
   times = subdivise(0, 300, 250)
   Y0 = (0, 400, 0)

   Ye = odeint(compute_dv, Y0, times)

   velocity = [y[0] for y in Ye]
   weight = [y[1] for y in Ye]
   altitude = [y[2] for y in Ye]
   
   plt.subplot(2, 2, 1)
   plt.plot(times, velocity, label="vitesse")
   plt.legend()

   plt.subplot(2, 2, 2)
   plt.plot(times, weight, label="masse")
   plt.legend()

   plt.subplot(2, 1, 2)
   plt.plot(times, altitude, label="altitude")
   plt.legend()

   plt.show()

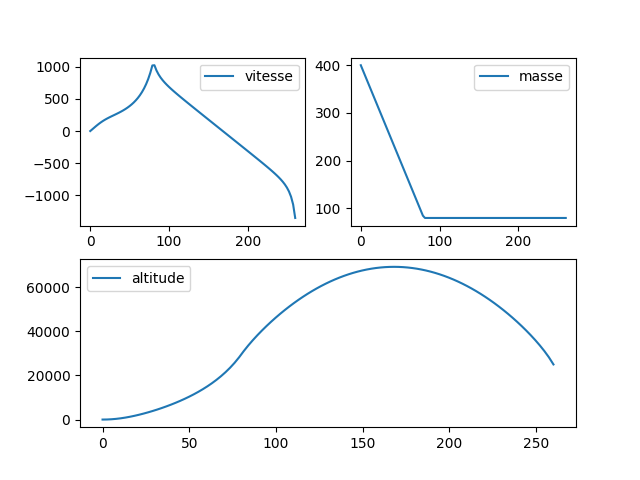
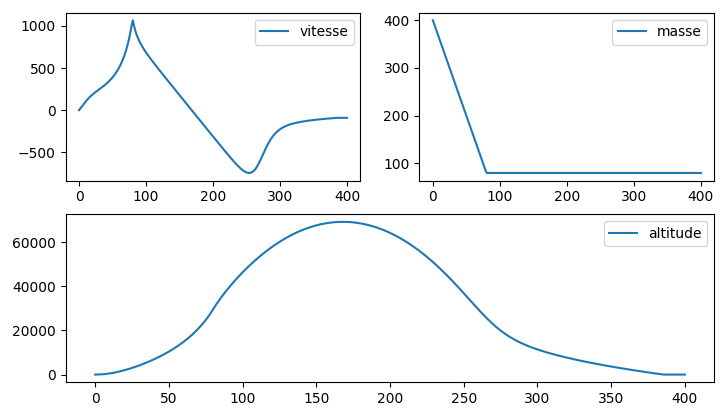
Ce qui me donne les courbes suivantes :

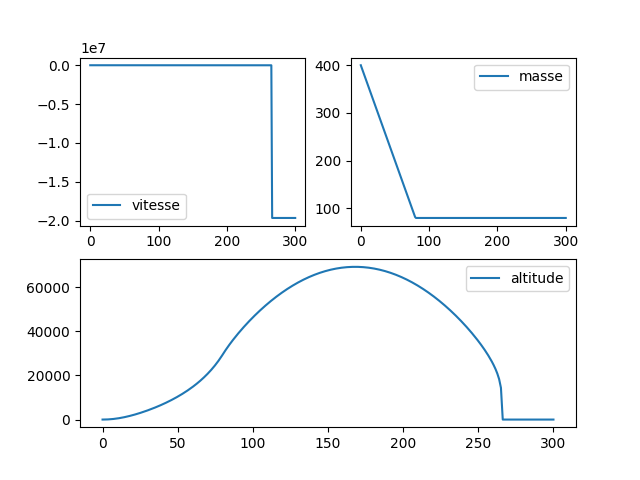
On peut voir que la vitesse donne n’importe quoi et je n’arrive pas à savoir pourquoi. Auriez-vous une idée ?

Merci pour votre aide !

Salut,

Le solveur te donne un indice, il donne ce warning :

lsoda--  warning..internal t (=r1) and h (=r2) are
      such that in the machine, t + h = t on the next step           
      (h = step size). solver will continue anyway
     in above,  r1 =  0.2657747190447D+03   r2 =  0.2339161631143D-13

Il dit que la machine n’est pas capable de différencier $t$ de $t+\delta t$ parce que $\delta t$ est relativement trop petit. Ça vient, je pense, de ta condition qui passe toutes les dérivées à $0$ lorsque tu arrives sur le sol. Remarque que ton code fonctionne très bien si tu t’arrêtes plus tôt (j’ai pris times = subdivise(0, 260, 100)) :

EDIT : en fait, cela vient de ton accélération qui tend vers l’infini, probablement à cause du $v^2$ dans le terme de frottements. Il y a quelque chose qui cloche dans tes équations… On voit sur le plot de la vitesse que l’accélération augmente furieusement sur la fin.

Pour ceux qui comme moi se sont interrogé sur la diminution de la vitesse (en valeur absolue) à la fin de la chute, je pense que ça simule la rentrée dans l’atmosphère.

Une fois les moteurs coupés, la vitesse de la fusée va diminuer, passer par 0 et atteindre une vitesse limite due aux frottements si ceux-ci ne dépendent que de la vitesse, donc jusqu’au choc, la vitesse devrait augmenter (en valeur absolue) jusqu’à un plateau. Là, on voit que la vitesse augmente bien dans un premier temps (en absolue), mais diminue ensuite ! Si je suis bien, ça vient du terme en $z$ dans l’équation : les frottements ne dépendent pas que de la vitesse ici. Les frottement diminuent à haute altitude, on simule ici la rentrée dans l’atmosphère (moins d’air, donc moins de frottement à haute altitude). On retrouve d’ailleurs ce $a_0$ à partir de la formule de la pression en fonction de l’altitude. $g$, lui, ne change pas, car 60 km, c’est peu devant les 6 000 km du rayon de la Terre.

Je n’ai souvenir d’avoir fait ça ; c’est amusant, en tout cas.

Merci pour votre aide ! En effet, les frottements sont toujours opposés à la vitesse, je n’hésiterais pas à le noter dans mon rapport !

Je me posais la même question que @Gabbro et j’en suis venu aux mêmes conclusions.. le point jaune correspond bien à une rentrée dans une atmosphère plus épaisse ?

J’ai dit plus épaisse car notre fusée ne dépasse pas les 100 km et est très loin des 800 km. Par conséquent elle est toujours dans l’atmosphère, du coup je trouve le terme rentrée dans l’atmosphère injustifié.

Merci pour tes explications en tout cas !

Une question intéressante peut être : est-ce que lors d’une rentrée atmosphérique, le point bas d’inversion de la courbe des vitesses correspond-il à max Q ? En tous cas, tu peux au moins indiquer que tes pointillés jaunes correspondent au point où l’augmentation des frottements (dûs à l’augmentation de la vitesse et de la densité atmosphérique) compensent l’accélération dûe à la gravité, et donc où ta fusée ralentit au lieu de continuer à accélérer. Ce sera sans doute plus clair si tu traces en plus la courbe d’accélération.

PS : on entend parler souvent d’atmosphère qui s’arrête à 100 km ou d’espace qui commence à 100 km (avec des variantes à 80 km ou 60 miles). C’est en fait à cause de la ligne de Kármán (et sa variante américaine) qui définit la limite officielle internationale (et aux USA) de l’espace. C’est pas un choix au hasard. Plus on va haut, moins l’atmosphère est dense, et plus on doit aller vite pour qu’un aéronef soit pilotable à l’aide de surface aérodynamiques. Arrive une altitude à laquelle cette vitesse est à peu près la même que celle de satellisation à la même altitude : c’est un point à partir duquel on ne peut plus piloter d’aéronef via des surfaces aérodynamiques aussi grandes soient-elles. On a arrondit tout ça à la louche pour donner un nombre rond facile à retenir, et voilà.

Il y a un projet de recalcul de cette altitude pour la définition internationale, qui viendrait probablement l’abaisser.

PPS : l’ISS comme presque tous les satellites en orbite basse ne sont même pas dans la couche la plus haute de notre atmosphère.

PPPS : en atmosphère terrestre, les freinages de rentrées atmosphériques depuis l’orbite commencent vers 80 km d’altitude et atteignent leurs maximums d’intensité vers 40 km. C’est différent avec ta fusée parce que n’étant pas orbitale, elle est beaucoup plus lente.