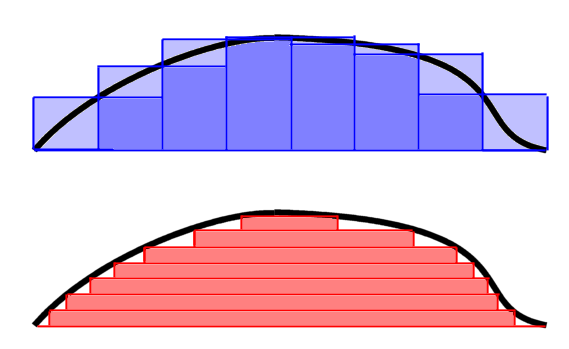
Bonjour,
Je suis dans les intégrales de Lebesgue et comprends de manière intuitive ce qu'est l'intégrale d'une fonction étagée positive (section 2.5), mais je bloque sur l'intégrale d'une fonction réelle Lebesgue-mesurable positive (section 2.6).
En effet, autant je visualise très bien comment on encadre une fonction avec des rectangles pour les intégrales de Riemann, autant je ne parviens pas à faire la correspondance avec la théorie de Lebesgue.
Auriez-vous un dessin pour illustrer cela ? Ou peut-être m'expliquer celui-ci ?
Merci.
+0
-0