Bonjour,
Je viens aujourd'hui avec un problème qui parait trivial, mais qui me bloque depuis une grosse heure.
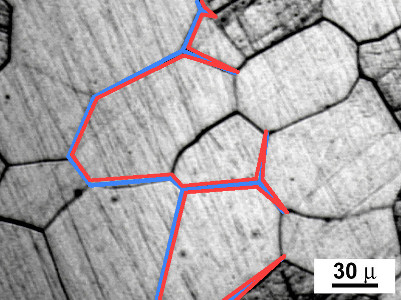
J'ai un ensemble de points, et pour chaque point, j'ai trois autres points auquels il est relié. Le résultat est un ensemble de polygones concaves. Le résultat me donne quelque chose similaire à ça.
Maintenant, j'aimerais pouvoir calculer l'air de chacun de ces polygones. Mon problème vient du fait que je ne sais pas quels points vont en former un ensemble.
Une suggestion d'algorithme ?
Merci
+0
-0