Bonjour à tous les Zéros Zesteux  !
!
Bossant actuellement sur les statistiques de test, quelques questions me viennent à l'esprit. Pour illustrer ces questions, je prendrai un exo corrigé que j'ai fait récemment.
Énoncé de l'exercice :
Le poids en gramme de 10 souris est relevé. On mesure à nouveau leur poids après 30 jours de régime alimentaire. On note X, le poids avant le régime, Y le poids après le régime et D la différence des poids (poids avant - poids après). Les variables X, Y et D sont supposées suivre des lois normales et les mesures indépendantes d’une souris à l’autre.
Les résultats figurent dans le tableau ci-dessous :
| X | Y |
|---|---|
| 31 | 29 |
| 34 | 29 |
| 37 | 31 |
| 39 | 42 |
| 39 | 35 |
| 40 | 34 |
| 42 | 38 |
| 44 | 40 |
| 45 | 36 |
| 49 | 53 |
On donne : $\sum x_i = 400 g$ et $\sum x_i^2 = 16254 g^2$
Voilà les points sur lesquels je voudrais que vous m'éclairiez :
-
On demande de calculer l'estimation de la variance de X. C'est simple à faire, mais je ne trouve pas le même résultat que dans la correction. En effet, cette dernière pose que $S^2(X) = \left( \dfrac{1}{n-1} \right) \left( \dfrac{\sum x_i^2 - \left( \sum x_i \right)^2}n \right) = \left( \dfrac{1}9 \right) \left( \dfrac{16254 - 400^2}{10} \right) = 28,22g²$ . Pourquoi divise-t-on par $n-1$ ?
-
On demande ensuite de déterminer si E(X) est statistiquement différent de 35, à un risque de 5%. Dans la correction, ils construisent la statistique de test de la manière suivante : $T = \dfrac{\bar X - 35}{\sqrt{S_X^2 \div n}}$ . Pourquoi divise-t-on par $\sqrt{n}$ ? Est-ce parce qu'il s'agit d'un test apparié ? Plus généralement, quand divise-t-on par $\sqrt{n}$ et quand ne le fait-on pas ?
Merci d'avance pour vos réponses qui, je n'en doute pas, seront aussi limpides que d'habitude  ,
,
Dwayn


 …
…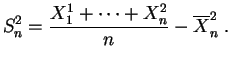 . En plus de ne pas comprendre où est passé le
. En plus de ne pas comprendre où est passé le 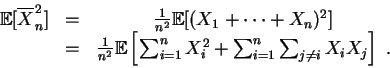 .
. )
)