Bonjour à tous 
Vos journées sont longues ? Les transports fatigants ? Les nuits pas assez excitantes ?
Venez donc jouer un peu, venez faire des maths !
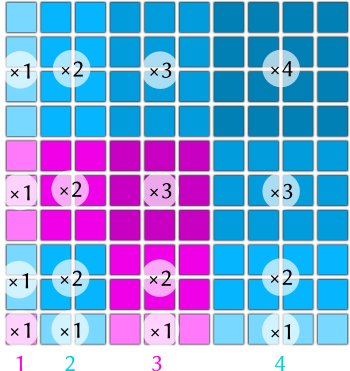
Pour cette première activité (grand public), je vous propose de démontrer (de la manière qui vous plaît la plus) l'égalité suivante :
où $n$ désigne un entier naturel.
Bien entendu, de multiples démonstrations sont possibles. Le but ici est que chacun puisse chercher dans son coin une solution. Et pour les meilleurs, en chercher une élégante et/ou étonnante (j'attends le premier qui utilisera les nombres de Betti).
Les règles pour jouer sont les suivantes :
- placer dans un bloc secret sa réponse ;
- faire un bloc (public) des pré-requis de la démonstration (par exemple sur l'identité $1+2+\dots+n = n(n+1)/2$ est un pré-requis) ;
- écrire entièrement la démonstration.
Ensuite vient le moment des relectures, chacun pouvant relire et commenter qui il veut, en plaçant bien entendu dans un bloc secret ses commentaires (pour ne pas spoiler la personne qui recherche).
Amusez vous bien !
Voilà ma réponse :
Pré-requis :
La formule est vraie pour $n=1$ puisque $1^2=1^3$. Supposons la formule vraie au rang $n$ (pour $n\geq 1$), au rang $n+1$ on obtient
on en déduit
il s'en suit
et comme $n^2+2n+1= (n+1)^2$ on conclut que
par récurrence, la formule est démontrée.



 Je ne mets pas la démonstration, c'est la même qu'au dessus.
Je ne mets pas la démonstration, c'est la même qu'au dessus.


 ), et il ne reste que
), et il ne reste que