Trouver une relation entre les solutions de l'équation x^y=y^x

Bonjour

J’essaie sans succès de résoudre dans $\bf{R}_{+} \backslash \{0\}$ l’équation $x^y=y^x$ où x, y sont des inconnues.

Pour résumer, j’ai montré dans un premier temps que résoudre cette équation revient à déterminer les réels x et y qui par la fonction $f: x \mapsto\displaystyle\frac{\ln x}{x}$ ont la même image.

L’étude des variations de f montre que celle ci est croissante sur $]0,e]$ (f tend vers $-\infty$ en 0, s’annule en 1 et atteint son maximum $1/e$ en $e$) puis est décroissante sur $[e, +\infty[$ (f tend vers 0 en $+\infty$).

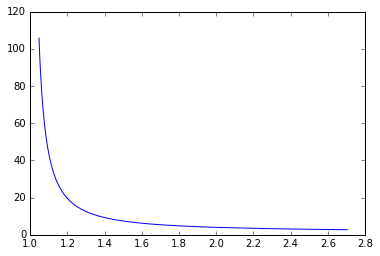
J’en déduit que si x est inférieur ou égal à 1 alors $y = x$ est solution de l’équation. Si x est supérieur à 1, d’après les variations de f, y est distinct de x [EDIT: ou x=y]. Mais je n’arrive pas à avoir une relation entre les deux solutions. Au mieux, graphiquement on peut se convaincre que si x est proche de e alors y l’est aussi (en étant supérieur à e), et que si x est proche de 1 (en étant supérieur à 1) alors y est très grand.

Dites moi si ce n’est pas très clair, ou ce que je pourrais mieux justifier.

EDIT: En fait je trouve quand même une relation faisant intervenir les deux solutions, mais je n’arrive pas à exprimer une solution en fonction de l’autre…

melepe: effectivement la solution y=x marche tout x, je l’avais remarqué comme solution ’evidente’ avant de me lancer dans l’étude de fonction, c’est un oubli.

blog yhg: super, je n’avais pas pensé à wolframalpha! Je vais essayer de comprendre pourquoi la fonction dont tu parles est liée à ce problème.

Je vous tient au courant.

Pour résumer, j’ai montré dans un premier temps que résoudre cette équation revient à déterminer les réels x et y qui par la fonction

On peut avoir le détail ?

@Holosmos Il utilise juste le fait que : $x^y=y^x \Leftrightarrow e^{\log x \cdot y} =e^{\log y \cdot x} $. Or puisque $x \mapsto e^x$ est invective alors cela revient à résoudre : $\log x \cdot y = \log y \cdot x \Leftrightarrow \frac{\log x}{x} =\frac{\log y}{y} $

@Universite: c’est exactement ça. Tu voulais dire injectif plutôt que "invectif"? À propos, vu que tu as toi aussi cet exercice dans tes fiches, est-ce que tu as essayé de le résoudre?

@ThomasC Qu’est-ce que tu entends par "résoudre" ? Il faut trouver une expression de l’autre solution de $\frac{\ln x}{x} = a$ en fonction de la première ?

Qu’est-ce que tu entends par "résoudre" ? Il faut trouver une expression de l’autre solution de $\frac{\ln x}{x} = a$ en fonction de la première ?

C’est bien ce que j’entends.

Je sais bien que c’est une faute de frappe, mais serait-il possible de ne pas la corriger tant elle est drôle ? \o/

@ThomasC Mais tu es certain que c’est une fonction élémentaire ? Regardes cet article : https://www.maa.org/programs/maa-awards/writing-awards/exponentials-reiterated-0 Je n’ai pas tout lu mais d’après ce que j’ai compris vers page 244 (10 sur le pdf), ils expriment leur solution avec la tétration infinie (pas élémentaire) et donnent un développement en série.

Correction. J’avais écrit "simple" au lieu de "élémentaire".

Et ça suffit pour faire pas mal de trucs non ? C’est pas très dur de montrer que les solutions positives de $x^y=y^x$ telles que $0<x<y$ sont les :

où $r$ décrit $\mathbf{R}_+^*$ (écrire $y=\left(1+\frac{1}{r}\right)x$). Géométriquement l’ensemble des solutions ressemble à :

Quand $r\to 0$, la paramétrisation tend vers $(1,\infty)$, et quand $r\to \infty$, ça tend vers $(e,e)$. Rien qu’avec cette forme implicite, on peut déjà donner pas mal d’infos sur la structure des solutions.