Collision entre deux points et énergie cinétique
Le problème exposé dans ce sujet a été résolu.
Connectez-vous pour pouvoir poster un message.
Connexion
Connexion
Pas encore membre ?
Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte

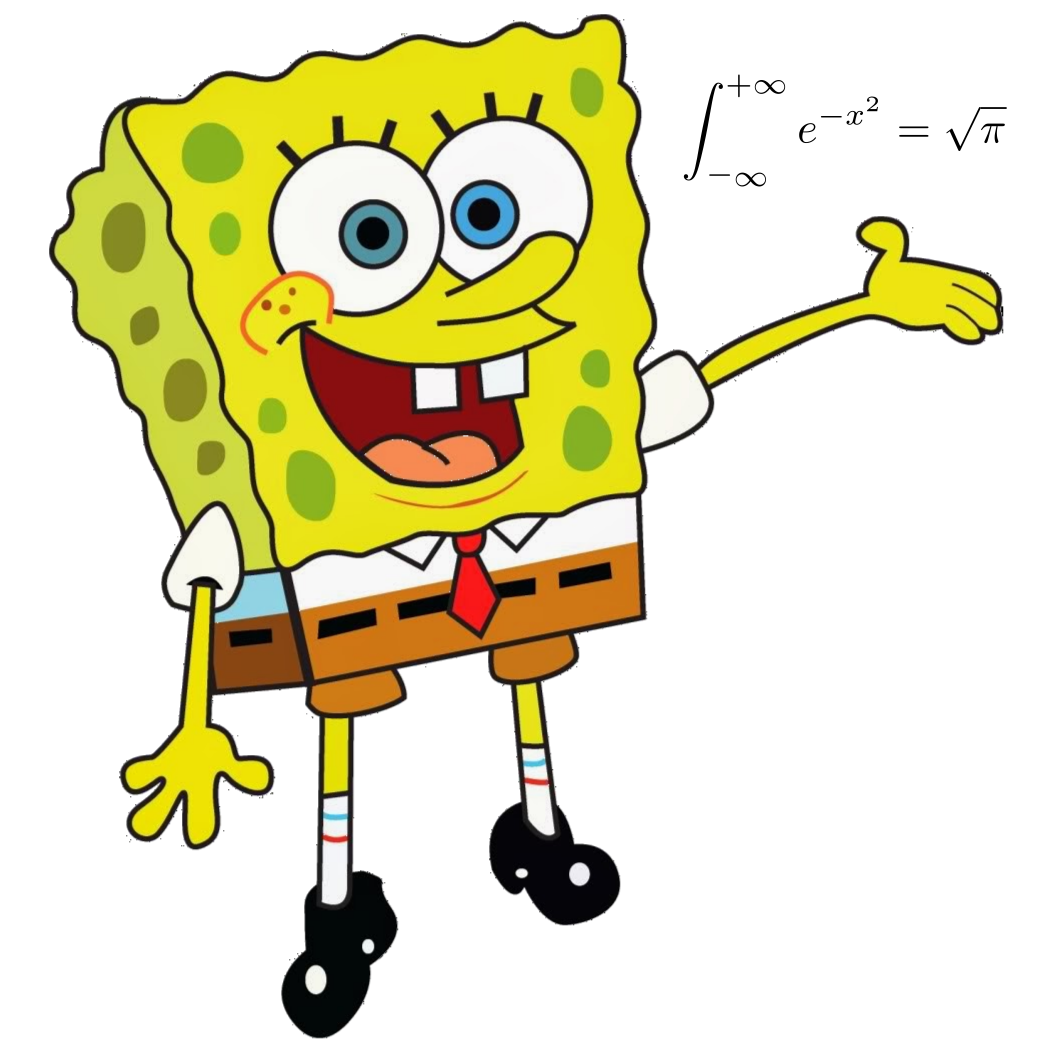

 !
!


 )
)