Les cartes sont d’abord de merveilleuses images pour rêver. – Gaston Rébuffat
La partie précédente présentait seulement les bases de la cartographie : choix de bons figurés, d’une bonne variable visuelle, etc. Tout cela nous donne déjà énormément de possibilités pour faire un nombre incalculable de cartes. Cependant, certaines situations complexes ont donné lieu à des pratiques encore plus poussées et tout aussi intéressantes.
- Les cartes en anamorphose et cartogrammes
- Discontinuités et cartes carroyées
- La représentation du réseau et son utilisation
- Représenter au delà de la carte : la matrice de Bertin
- Construire des cercles aux aires proportionnelles
Les cartes en anamorphose et cartogrammes
On a vu jusqu’ici différentes représentations graphiques mettant toutes en jeu des figurés qui se superposaient au-dessus d’un fond de carte. Néanmoins, on pourrait se dire qu’il est plus pertinent de modifier directement ce fond de carte. C’est le cas des anamorphoses et des cartogrammes.
Anamorphose : déformation de l’image, de telle sorte qu’un processus (déformation, réflexion dans un miroir, etc.) soit nécessaire pour la rendre normale.
Un des cas les plus fameux de l’anamorphose est le tableau Les Ambassadeurs, de Hans Holbein le Jeune.

Vous voyez l’objet bizarre, au pied des ambassadeurs ? C’est un crâne, visible sous sa forme normale lorsqu’on regarde le tableau dans un angle précis !
De même, on est obligé de déformer certains éléments sur une carte : par exemple, sur les cartes routières, les routes sont bien plus larges que la réalité, pour qu’elles soient bien visibles ! D’ailleurs, la largeur desdites routes dépend de leur importance : une autoroute sera plus large qu’une départementale et ainsi de suite.
On utilise ce procédé de déformation en cartographie, notamment en statistique. C’est ce qu’on appelle le cartogramme.
Cartogramme : carte dont le fond de carte ne se base pas sur la surface des territoires étudiés, mais de la variable étudiée. Par exemple, plus la population est élevée à un endroit, et plus cet endroit sera graphiquement étendu. Il existe deux types de cartogrammes : le premier est basé sur une variation de surface, le second sur une variation de distance. Prenons un exemple pour clarifier : dans le premier cas, on va agrandir ou réduire une surface selon nos données (la carte de nos continents un peu plus bas). Dans le second cas, on va réduire la distance entre plusieurs points (la carte du réseau ferroviaire, elle aussi un peu plus bas).
Un cartogramme peut être simple ou complexe à réaliser : nous commencerons, nous, avec un cas simple. On définit un carré de base, par exemple 1 cm sur 1 cm, correspondant à une valeur, 50 millions d’habitants ; le nombre de petits carrés représente la population totale. Ainsi, on a une relation entre des données quantitatives et une surface.
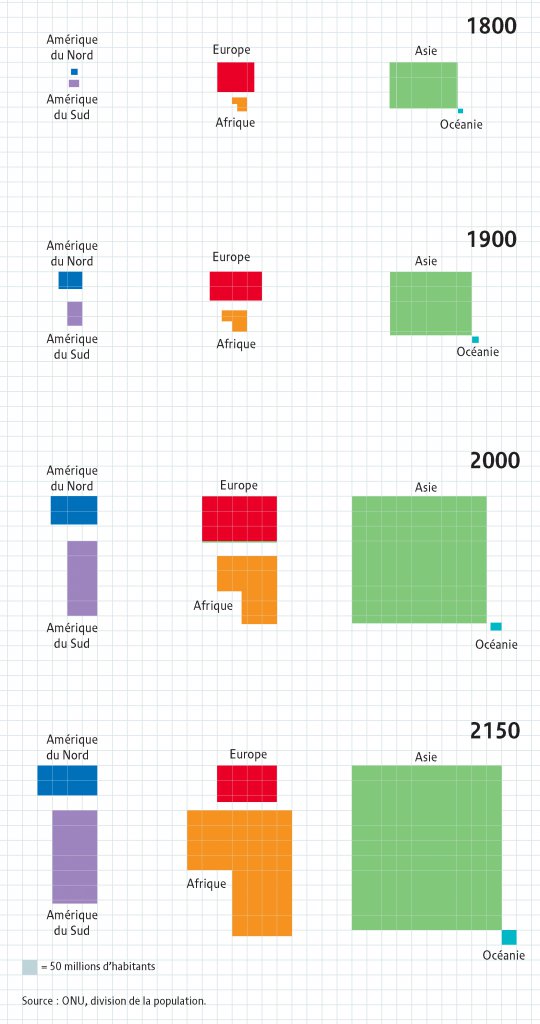
Il existe des variantes, comme le cartogramme de Dorling, remplaçant les carrés par des cercles proportionnels aux variables (voir annexe pour les calculs) :
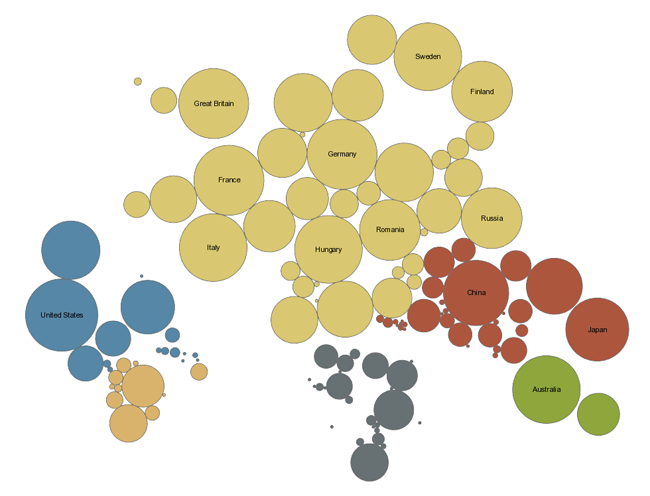
Malgré, cette méthode, bien qu’assez esthétique, rend la carte difficilement lisible : on identifie mal l’espace de départ (pays, région, etc.) et, de facto, on est obligé de nommer les cercles. Néanmoins, on perçoit bien les différentes quantités.
Dans cet exemple, on fait varier l’étendue. On peut aussi faire varier les distances :
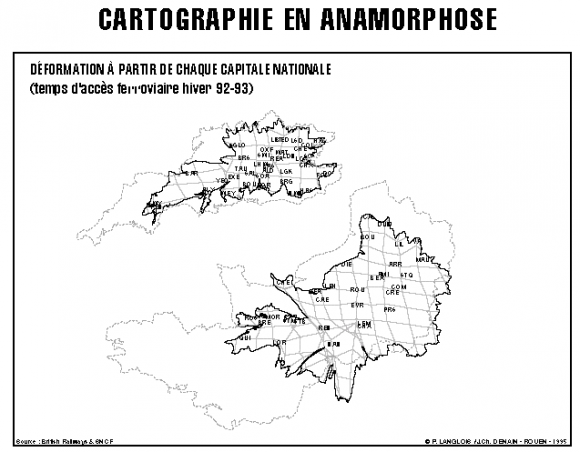
Un désagrément de cette méthode est de rendre la carte difficilement interprétable : on a moins de facilité à lire les valeurs.
On peut imaginer faire des cartes où les éléments proches graphiquement sont ceux qui ont un temps de trajet court, tandis que ceux éloignés graphiquement sont ceux avec un temps de trajet long. On verrait des distorsions de l’espace. Dans ce cas, on pourra réaliser un cartogramme pour représenter ce phénomène. Attention néanmoins : ici, il ne faudra pas mettre une échelle spatiale, car la notion de distance n’est pas pertinente : on privilégiera une échelle temporelle par exemple.
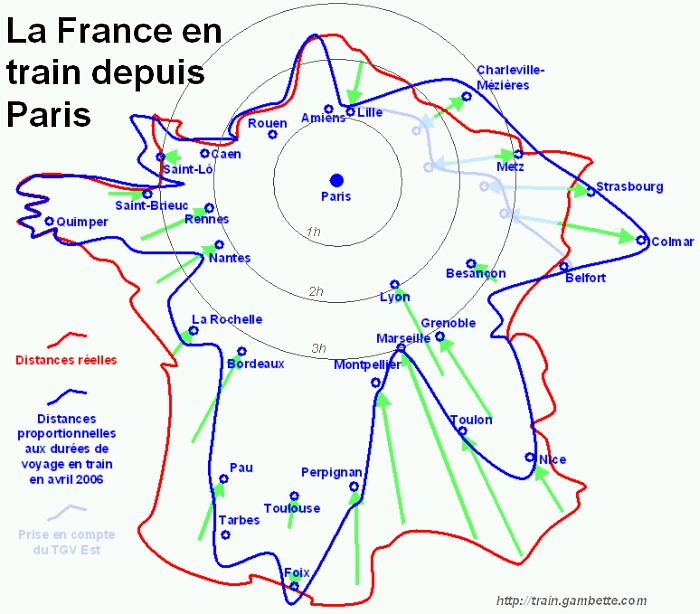
On peut aussi complexifier la chose et jouer à partir d’un fond de carte préexistant, en « gonflant » certains espaces. Ici, on fait varier l’étendue, mais cette fois sur un fond de carte préexistant.
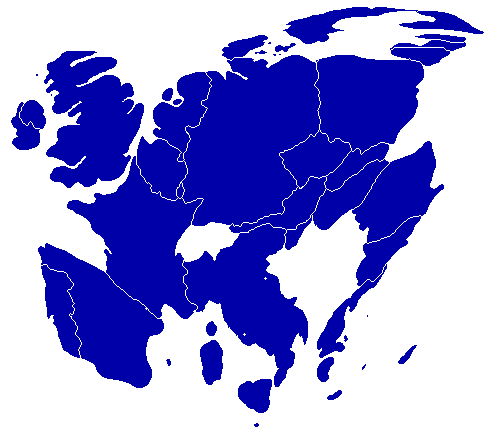
Cette dernière carte semble être le meilleur choix. En effet, on garde l’aspect carte, en ayant une bonne visibilité de l’information. Néanmoins, elle peut être difficilement lisible pour un néophyte et ardue à réaliser sans informatique.
On a mis longtemps à trouver le bon algorithme pour créer des cartogrammes (la page anglophone Wikipédia en dresse une typologie), car plusieurs problèmes se posaient, par exemple la superposition de différents polygones. N’étant pas expert en mathématique, je ne pourrais que difficilement vous expliquer les différentes méthodes : du moins, de ce que j’ai compris, une méthode couramment utilisée est de superposer une grille à un fond de carte. En déformant la grille, on déforme le fond de carte.
Dans la pratique, on fait comment ? On peut réaliser une carte simple, cartogramme classique avec des carrés ou des cercles à la main ou à l’aide d’un logiciel de dessin. On peut aussi utiliser un logiciel de SIG (système d’information géographique) qui fera les calculs pour nous. À la fin du tutoriel se trouve une bibliographie, avec un cours dédié à cette pratique, pour ceux que ça intéresse ! Il existe aussi le logiciel ScapeToad pour faire rapidement ce genre de cartes.
Jusqu’ici, on a vu la déformation des mailles comme méthode de représentation. Néanmoins, on peut aussi voir le problème autrement, et redessiner les mailles de notre carte : c’est le but du carroyage.
Discontinuités et cartes carroyées
Le carroyage, c’est découper l’espace en carrés via un quadrillage pour ne plus dépendre d’un découpage administratif, variable selon les instituts (administrations étatiques et privées) ou de l’évolution temporelle des frontières. On le fait généralement de manière automatisée.
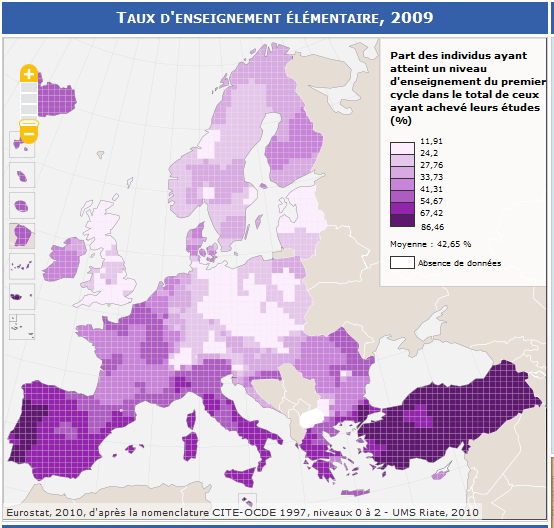
Concrètement, comment réaliser une carte carroyée ? On prend un fond de carte, et par-dessus on applique un quadrillage (250 × 250 km par exemple).
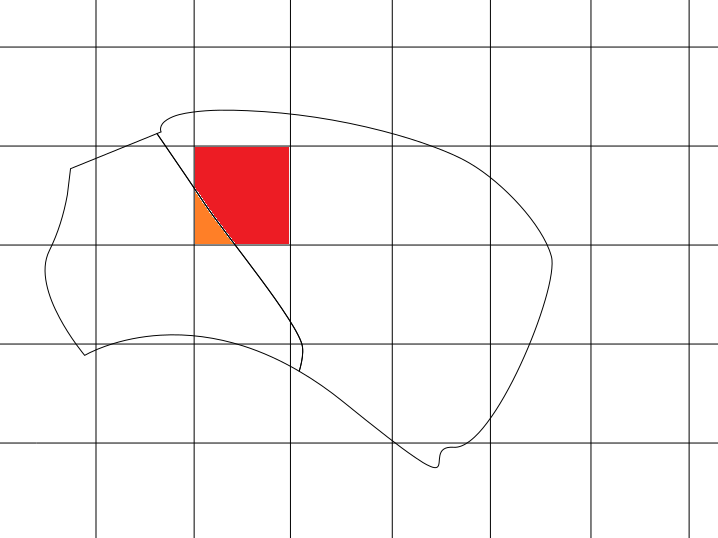
On voit, dans la partie colorée, un problème : le carré enjambe une frontière, avec 20 % pour la partie orange et 80 % pour la partie rouge. Pour déterminer la valeur du carré, on va faire A × 0,2 + B × 0,8. Attention, on ne peut faire ça qu’avec des valeurs quantitatives absolues !
Pour les discontinuités, on va non pas découper l’espace en carrée, mais on va faire une division par lieux de ruptures, de tensions (inégalité de richesse, rupture climatique…). Pour y arriver, on va chercher des statistiques d’un maillage assez fin.
La représentation du réseau et son utilisation
Dans la plupart des cas présentés précédemment, on se contentait de représenter de manière fixe les choses. On prenait une photo à un instant T et c’était une affaire classée ; à la rigueur, on faisait une collection de cartes à différents moments. Pourtant, cette méthode ne peut pas s’appliquer sans inconvénient lorsque l’on veut représenter quelque chose en mouvement. Et justement, puisqu’un objet en mouvement c’est un flux, nous allons parler de la représentation des flux.
Flux : déplacement de marchandises, de biens, de personnes, de capitaux, d’idées…
Mais complexifions encore la chose : pourquoi n’y aurait-il qu’un seul flux de représenter ? Lorsque plusieurs flux sont combinés, on parle de réseau : c’est tout un système de circulation qui passe par ces réseaux. On ne représente plus une carte de manière à représenter l’espace en tant que territoire, mais en tant que réseau. Ici, on ne va plus représenter par exemple la distance entre un point A et B, mais plutôt la nature de cette relation, comme le temps de déplacement ou la quantité d’objets traversant en un temps donné.
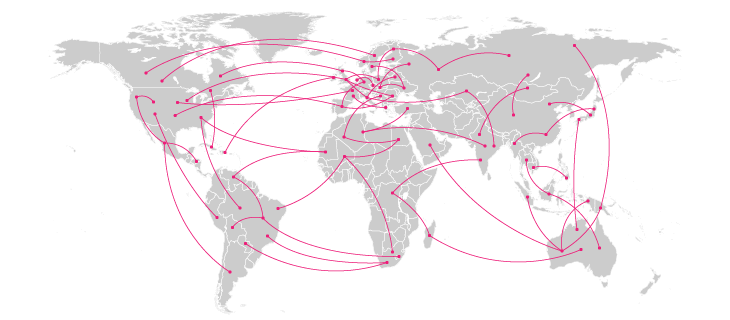
Dans la carte ci-dessus, on représente le déplacement d’un point A à un point B, de manière spatialisée.
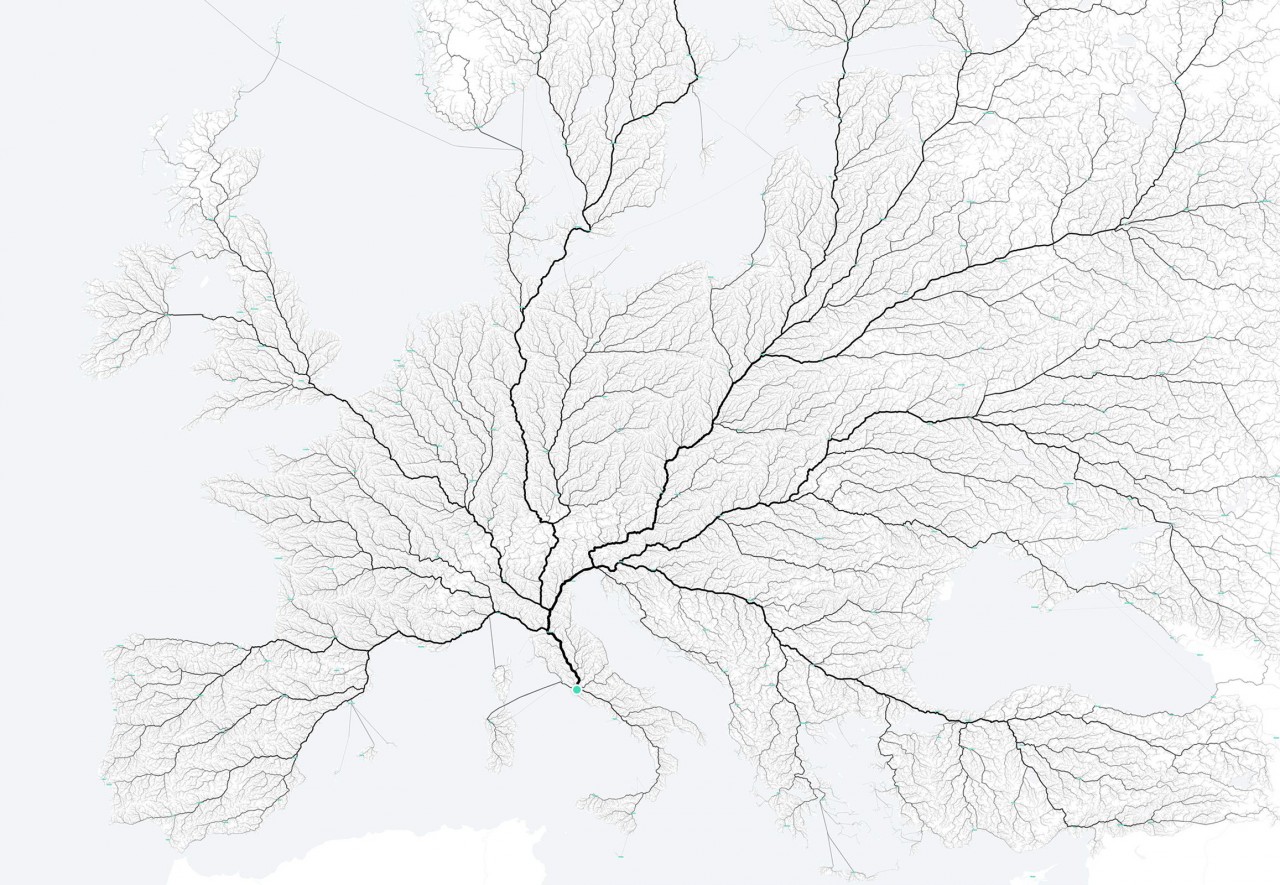
Dans la carte ci-dessus, on représente l’infrastructure routière et non son utilisation.
Il est aussi possible de traiter, non pas de l’infrastructure en tant que telle (routes, câbles…), qui est fixe, mais de l’utilisation qui en est faite (trafic). Un réseau doit comporter 2 caractéristiques importantes : la connexité, c’est-à-dire qu’à partir de n’importe quel point du réseau on peut aller à un autre (tous les chemins mènent à Rome), et la connectivité, c’est-à-dire le nombre de possibilités alternatives, sa redondance, sa résilience.
En fait, l’élément central, dans cette sous-partie, est le réseau, et non la carte : en effet, on peut choisir de s’affranchir des distances, du spatial, pour mieux se focaliser sur les flux. On peut donc faire une carte sans avoir de notion de distances, c’est-à-dire sans fond de carte, schématiquement.
On va donc cartographier le réseau de manière schématique, sans fond de carte.
Un exemple simple : pour représenter les trajets de bateaux de port en port, il suffit de tracer une droite graduée, sur laquelle on place les différents ports. Ensuite, il suffit de relier les ports par des arcs pour représenter les trajets en question. Si, en plus, il est nécessaire de montrer un flux quantitatif, on prendra comme variable visuelle la taille de mon arc ! Nous nous sommes donc affranchis des contraintes spatiales : qu’importe si Shanghai se trouve ou non à côté d’Amsterdam, il suffira de relier les deux points si le trajet est direct !

Représenter au delà de la carte : la matrice de Bertin
Cette méthode-ci a pour principe central la lisibilité de la carte : le document graphique doit être compris en un coup d’œil et non être lu.

Il se peut que pour collecter une information, nous devions faire un tableau, sous forme matricielle. Ainsi, si on étudie différents espaces (A à P), on peut noter la présence (en noir) ou non (en blanc) d’un certain nombre d’attributs (en l’occurrence, des bâtiments et des infrastructures). Mais vous pouvez vous-même vous rendre compte que la lecture n’est pas pratique : aucune tendance ne se dégage en un coup d’œil. Il faut donc réorganiser tout ça.

On va donc ordonner de manière verticale et horizontale les différentes données :

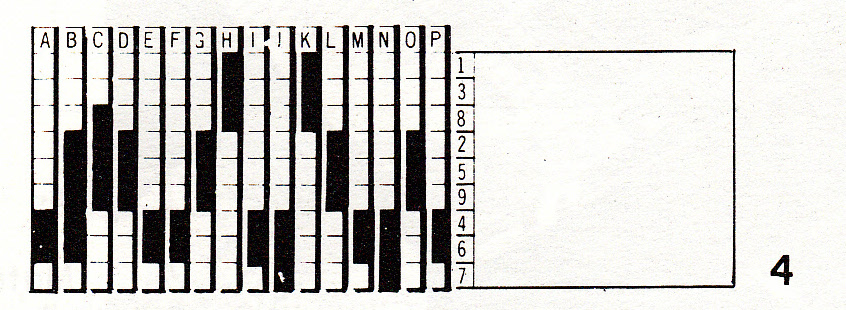

On voit se dégager différents ensembles, que l’on va organiser et classifier selon leur nature :

Dit comme ça, vous allez me demander le rapport à la cartographie (et vous avez raison !). En fait, la matrice de Bertin peut-être utile dans divers cas liés à la cartographie : pour traiter et comprendre les informations de manière préliminaire, afin de découvrir des pistes de réflexion. Cependant, on pourra utiliser notre matrice remodelée en guide de légende, pour guider le destinataire dans la compréhension de la carte.
Bien sûr, cela peut sembler étrange de voir cette représentation sur un cours sur les cartes. Néanmoins, le rapport y est : on représente des données spatialisées et l’on met en évidence un certain nombre d’informations. Ajouter de la complexité, en mettant des données quantitatives (donc variation de valeur), pour compter le nombre de collèges ou autre dans un lieu, peut être une piste d’utilisation. Des fois, il peut être plus pertinent de montrer à l’usager final une matrice qu’une carte. À vous de choisir ce qui est le plus compréhensible et le plus pertinent !
Construire des cercles aux aires proportionnelles
On peut, pour représenter des quantités de données, faire des cercles aux aires proportionnelles. Si on veut représenter un cercle de valeur 100 et un autre de valeur 1 000, il doit avoir un rapport de 10 entre ces deux cercles. Mais dans le cas d’une grosse disparité (rapport de 1000 par exemple), il est impossible de faire cela : on va donc utiliser un coefficient multiplicateur pour calculer la taille de nos cercles.
1) On calcule notre coefficient.
On va donc utiliser la formule
où Q est la quantité à cartographier et R le rayon du cercle de référence (généralement le plus grand ou le plus petit) que l’on souhaite attribuer.
Exemple : On a une ville de 200 000 habitants, et on veut un rayon de 5 cm.
Notre coefficient vaut donc 8 000.
2) On applique ce coefficient à toutes les valeurs de la série.
Si on a une ville de 25 000 habitants, on fait :
pour Paris :
In fine, nous avons quelques pratiques cartographiques avancées, qui permettent de surmonter un certain nombre d’obstacles ; cela sert également à diversifier les cartes possibles. C’est ça qui est enthousiasmant avec la cartographie : vous n’avez aucune limite, si ce n’est la lisibilité ! Tant que la pertinence est là, vous pouvez tout faire  .
.