Et maintenant, on va voir quels composants sont nécessaires pour réaliser des circuits logiques au niveau électronique, et un peu s’intéresser à ce qu’il y a dedans.
Ce chapitre tient, pour la plupart, de la culture générale, donc si vous le souhaitez, vous pouvez directement sauter à la dernière partie qui présente les portes logiques sans s’inquiéter de ce qu’il y a dedans (parce qu’en pratique, peu importe). Par ailleurs, différents chapitre du MOOC fabrication numérique explorent de manière plus détaillée la partie « circuits », tandis que le tutoriel d’Aabu sur les panneaux photovoltaïques explique le principe de fonctionnement d’un semi-conducteur.
- La version « interrupteurs »
- Semi-conducteurs et diodes
- Jonctions et transistors à effet de champ
- Des portes, des portes et des portes !
La version « interrupteurs »
Comment représenter une variable propositionnelle au niveau de la machine ? Cela n’est pas très compliqué en soi, il suffit d’avoir un objet ou un signal possédant 2 états différents, un on (ou 1, ou « vrai ») et un off (ou 0, ou « faux »). L’idée la plus simple est alors de dire, par exemple, que la présence du courant correspond à 1 et l’absence de courant à 0.
Pour visualiser ça, pas besoin d’aller très loin. Il suffit d’imaginer un circuit électrique tout simple:
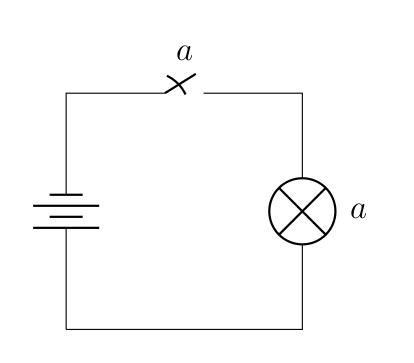
Bon, pas besoin d’avoir fait Bac+5 ingénieur pour imaginer ce que fait ce circuit, non ? Si ? Allez : si l’interrupteur est ouvert, la lampe ne s’allume pas, s’il est fermé, le courant passe et elle s’allume. Sauf que c’est beaucoup moins idiot qu’il n’y parait : si l’interrupteur représente une variable , la lampe représente le résultat (donc ici ). Et avec un tout petit peu plus de matériel, on peut commencer à faire des choses intéressantes. Par exemple, le circuit suivant.
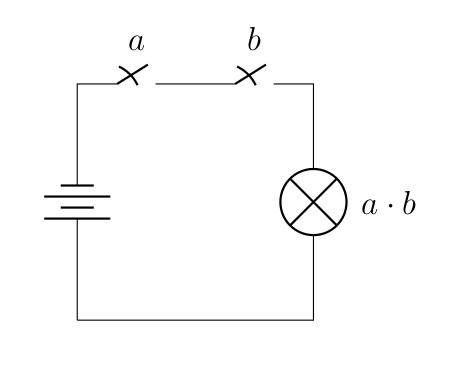
Repartons du principe que chaque interrupteur représente une variable. Qu’est ce qui se passe si on teste les différentes possibilités de positions pour chacun des interrupteurs ?
| Interrupteur | Interrupteur | Lampe |
|---|---|---|
| Ouvert | Ouvert | Éteinte |
| Ouvert | Fermé | Éteinte |
| Fermé | Ouvert | Éteinte |
| Fermé | Fermé | Allumée |
Ceux qui ont une bonne mémoire se souviendront alors que ça ressemble fortement à la table de vérité du connecteur ET, pour la simple et bonne raison que c’est comme ça qu’on s’en sortirait en utilisant des interrupteurs. De la même manière, le circuit suivant donne la version électrique du connecteur OU.
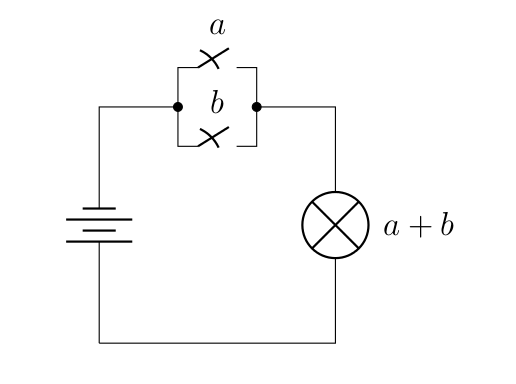
Vous pouvez vérifier, ça correspond bien à la même table de vérité
| Interrupteur | Interrupteur | Lampe |
|---|---|---|
| Ouvert | Ouvert | Éteinte |
| Ouvert | Fermé | Allumée |
| Fermé | Ouvert | Allumée |
| Fermé | Fermé | Allumée |
C’est bien équivalent à la table de vérité du connecteur OU : éteint uniquement si les deux interrupteurs sont ouverts, autrement dit .
Pour être totalement complet, voici finalement un circuit possible pour la négation (on est obligé d’utiliser un interrupteur un peu différent).
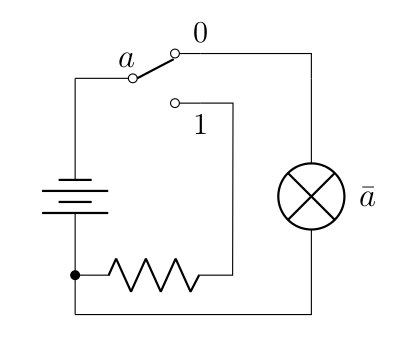
Donc, avec un certain nombre d’interrupteurs, des lampes et beaucoup de fils, on est capable de transformer n’importe quelle fonction logique en un circuit équivalent. Pas mal, non ? Pas mal, en effet, mais un peu trop beau pour être vrai. Même si le principe est à peu près équivalent, on a développé des solutions beaucoup plus facile à utiliser (mais rien ne vous empêche d’essayer, je vous renvoie au MOOC fabrication numérique pour les motivés).
Semi-conducteurs et diodes
Petits rappels d’électricité
Vous savez sans doute que l’électricité, ce n’est jamais qu’un déplacement d’électrons, ces petites charges négatives qui constituent la matière qui nous entoure en étant une des particules de l’atome (avec le proton et le neutron). Dans tout circuit électrique, les électrons se déplacent avec une certaine intensité, qui équivaut au nombre d’électron déplacés de la source à la destination. Cette intensité, est mesurée en ampère, qui correspond au nombre de charges par unités de seconde, donc à un « débit » (voir une vitesse) de charge. Un peu comme un robinet que vous ouvririez plus ou moins fort.
À noter que le sens conventionnel du courant est défini comme étant l’inverse du sens physique : les électrons se déplacent du pôle négatif au pôle positif, mais le courant part de la borne positive vers la borne négative.
Une seconde grandeur intervient, c’est la tension, , qui est l’énergie qu’on applique pour déplacer les électrons, que vous connaissez par son unité, les volts. Une manière autre de le voir, c’est celle du pôle positif/négatif (+/-), les électrons étant attirés par la tension positive et repoussés par la tension négative. Cette tension se mesure entre deux points dans un circuit électrique. Elle est fonction de l’intensité du courant qui circule entre les deux points et de la résistance du circuit entre ces deux mêmes points, par la célèbre loi , où est la résistance (en ohms).
Les lois de l’électricité énoncent que la somme des courants entrant dans un circuit est égale à la somme des courant en sortant, tandis que le potentiel global d’un circuit fermé doit être nul (parce qu’il y a conservation de l’énergie). Dès lors,
- En série, l’intensité est la même en tout points du circuit, et les potentiels s’additionnent.
- En parallèle, la tension entre les branches est la même, mais les intensités s’additionnent et leur somme est égale à l’intensité au niveau des nœuds.
Des semi-conducteurs tout partout !
Dans la réalité un électron ne se déplace pas réellement d’un bout à l’autre du circuit. La réalité serait en effet plus proche d’une grande file où les électrons avanceraient petit à petit, en rencontrant plus ou moins de résistance. Et de résistance, il va justement en être question En effet, un matériau dit résistant, c’est donc un matériau dans lequel le déplacement des électrons est difficile1, voire impossible. À l’inverse, un matériau est dit conducteur si le déplacement des électrons dans celui-ci est facile. Les matériaux conducteurs, vous les connaissez bien, c’est par exemple le cuivre (le moins cher des trois), l’argent ou l’or. Et un matériau semi-conducteur, ben c’est entre les deux : là où une tension très faible suffit à faire circuler les électrons dans un conducteur, il faut atteindre une certaine tension seuil pour faire circuler le courant dans un semi-conducteur.
Pour visualiser ce qu’il se passe dans ces matériaux semi-conducteurs, on peut imaginer que les électrons circulent en passant de trous en trous, qui sont autant de défauts dans la structure du semi-conducteur. Ces « trous » peuvent être vu comme des charges positives, parce qu’il s’agit d’endroit microscopiques dans la structure du matériau où on constate une absence d’électron (défaut de charge négative = charge positive).
Par défaut, la tension à appliquer pour qu’un semi-conducteur soit utilisable est un peu trop importante pour qu’elle soit intéressante. Comme dans le sport, on a alors recours au dopage et il existe deux manière de faire :
- Dopage n : on augmente le nombre d’électrons disponibles dans le semi-conducteur en question. On parle alors de porteurs de charge majoritaires négatifs et de porteurs de charge minoritaires positifs.
- Dopage p : à l’inverse, on augmente le nombre de trous.2
Là où ça devient intéressant, c’est qu’on peut alors créer une « jonction pn », soit un assemblage entre un semi-conducteur dopé p et un semi-conducteur dopé n. Schématiquement, on obtient quelque chose du genre.
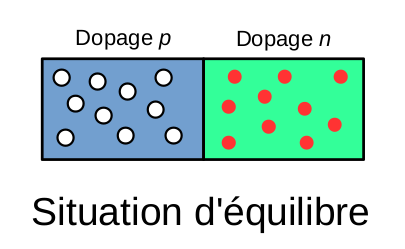
Quelque chose d’intéressant à noter, c’est que cette jonction ne réagit pas de la même manière si on lui applique une tension dans un sens ou dans l’autre.
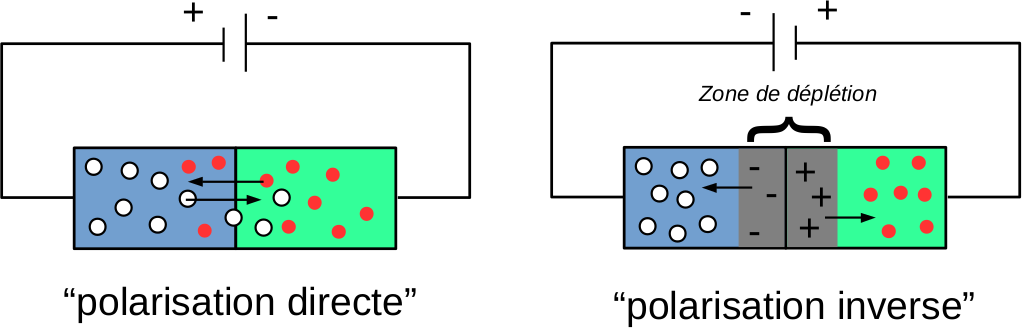
Qu’est ce qui se passe ? Quand on est dans le sens de la polarisation directe, la borne positive attire les charges négatives, les électrons, à travers le semi-conducteur p. Les trous, quand a eux, ne se déplacent pas, mais comme les électrons sont attirés, ils laissent derrière eux des trous inoccupés, d’où l’impression qu’ils se déplacent également vers la borne négative. Mais quand on applique la tension dans l’autre sens (polarisation inverse), rien ne va plus ! Les électrons, toujours attirés par la borne positive, se déplacent dans cette direction, laissant des trous dans le semi-conducteur p derrière eux, et les électrons du semi-conducteur n font de même, laissant derrière eux une zone appelée zone de déplétion et qui contient les porteurs de charges minoritaires (de signes opposés, mais en nombre moins importants). Autrement dit, dans ce sens-là, les porteurs de charge majoritaires s’éloigne de la jonction, ce qui a pour effet que le courant ne passe plus dans le matériau.
On a donc un matériau qui laisse passer le courant dans un sens (quand le semi-conducteur p est relié à la borne Positive et le semi-conducteur n est relié à la borne Négative, notez la mise en évidence) et pas dans l’autre, ce qu’on appelle aussi une diode.
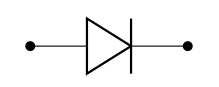
Dès lors, dans ce schéma de la diode, qui représente une flèche, définit le « sens passant » si le potentiel à gauche est plus important (plus positif) que celui de droite (sens conventionnel du courant).
Historiquement, les diodes étaient à la base des tubes sous vides dans lesquels un flux d’électron parcouraient le vide entre une anode et une cathode à condition que la tension entre ces deux composants soit suffisamment importante. On les retrouve encore aujourd’hui, par exemple dans les amplis dit « à lampe » pour joueurs de guitare.
Faire des circuits logiques avec des diodes
Ces diodes permettent déjà d’implémenter d’une manière différente les portes logiques citées plus haut (voir à ce sujet l’article Wikipédia correspondant (en) si ça vous intéresse). Ainsi, voici par exemple un montage qui représente un connecteur OU et un ET.
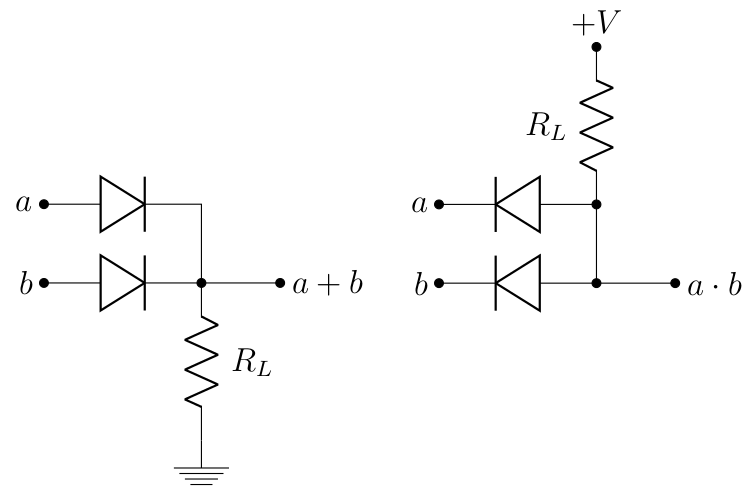
Le schéma associé à OU est plus facile à comprendre : s’il n’y a aucune tension appliquée sur ou , aucun courant ne passe et la sortie est également à une tension de 0 volt, ce qui correspond à « faux ». Si on applique cette fois une tension positive sur et/ou , la tension mesurée en sortie sera également positive, ce qui correspondra à « vrai ».
Le schéma associé à ET est juste un tout petit peu plus complexe : s’il n’y a aucune tension appliquée sur ou , la tension est dissipé à travers les diodes, par les lois associées aux tensions, il n’y a pas de tension en sortie. Cela reste vrai tant qu’une tension positive n’est pas appliquée sur chacune des deux entrées et .
En pratique, les montages utilisant les diodes ne sont plus utilisés, les diodes possédant une certaine résistance, provenant du passage des charges dans le semi-conducteur (autrement dit, elles ont besoin d’une tension minimale pour être actives, tout comme leur équivalent sous forme de tube à vide, quoique moins importante que ces derniers).
- À l’impossible, nul n’est tenu : quand la tension est très importante, tout est possible.↩
- En vrai : on a un matériau fait de SiO2 cristallin, le silicium ayant 4 électrons de valence chacun liés à un oxygène. Si on inclut dans le réseau cristallin des atomes de la 5ième colonne du tableau périodique (5 électrons de valence), il y a donc un électron de valence « de trop », donc un excès. À l’inverse, si on inclut dans la structure des atomes de la 3ième colonne du tableau périodique (3 électrons de valence), on crée un trou. Rien de compliqué.
↩
Jonctions et transistors à effet de champ
L’idée du semi-conducteur était quand même bonne et on va voir comment il est possible de l’exploiter de manière plus efficace.
Les transistors bipolaires
On va donc assembler, à la suite, un premier semi-conducteur qu’on va doper de manière assez importante et qu’on va appeler, de ce fait, l’émetteur (E), suivit d’un semi-conducteur de dopage opposé, relativement fin, et qu’on appellera la base (B), puis finalement un troisième émetteur de même type de dopage que le premier, qu’on appellera le collecteur (C). La jonction peut donc être de type NPN ou PNP, en fonction du dopage du premier semi-conducteur1.
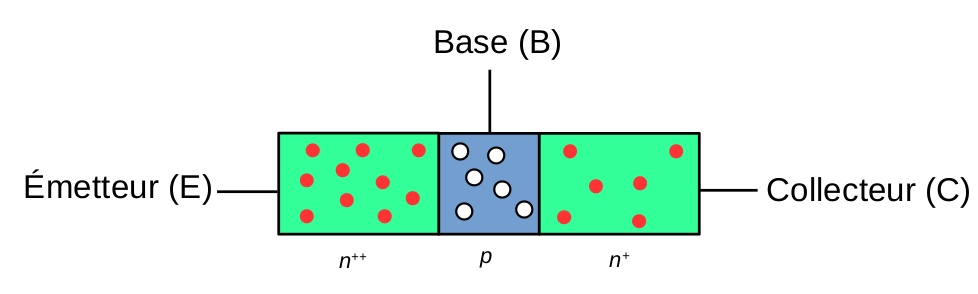
On forme alors des transistors2 dit « bipolaires » du fait qu’ils possèdent 3 points de contacts, contre deux pour les éléments de circuits plus classiques qu’on a rencontré jusqu’ici.
On a vu plus haut que pour qu’il y ait passage du courant, la jonction doit être polarisée dans le sens direct. On se doute donc bien que si le potentiel de la base () est plus négatif que celui de l’émetteur () et du collecteur (), rien ne se passe (). Néanmoins, c’est en jouant sur le potentiel de la base que cette jonction révèle tout son… Potentiel.
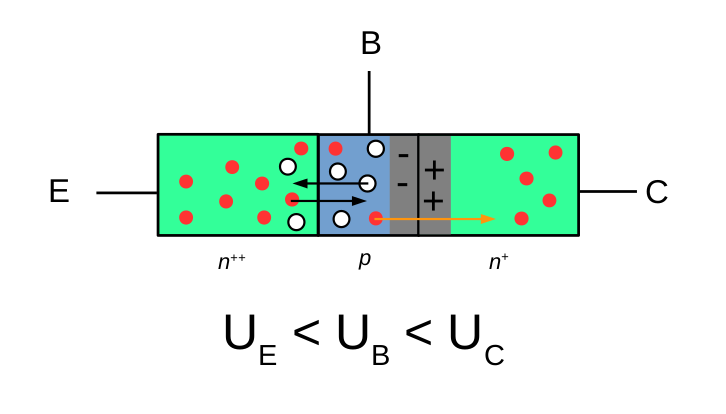
Ce qui est très intéressant, c’est qu’on a un dispositif qui peut alors jouer le rôle d’un interrupteur, en laissant passer le courant ou non en fonction du potentiel appliqué à la base3. Ainsi, si on reste dans le cas d’un transistor NPN, le potentiel du collecteur étant fixé comme supérieur à celui de l’émetteur et de la base, l’interrupteur est fermé si la tension appliquée à la base est supérieure à celle de l’émetteur () et ouvert si cette tension est inférieure (). Il est donc assez logique d’imaginer qu’on puisse s’en servir pour créer un circuit. Dans ledit circuit, une jonction npn se représente comme suis.
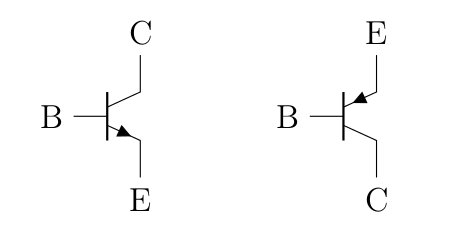
Et voici donc les circuits correspondant aux différents composants logiques.
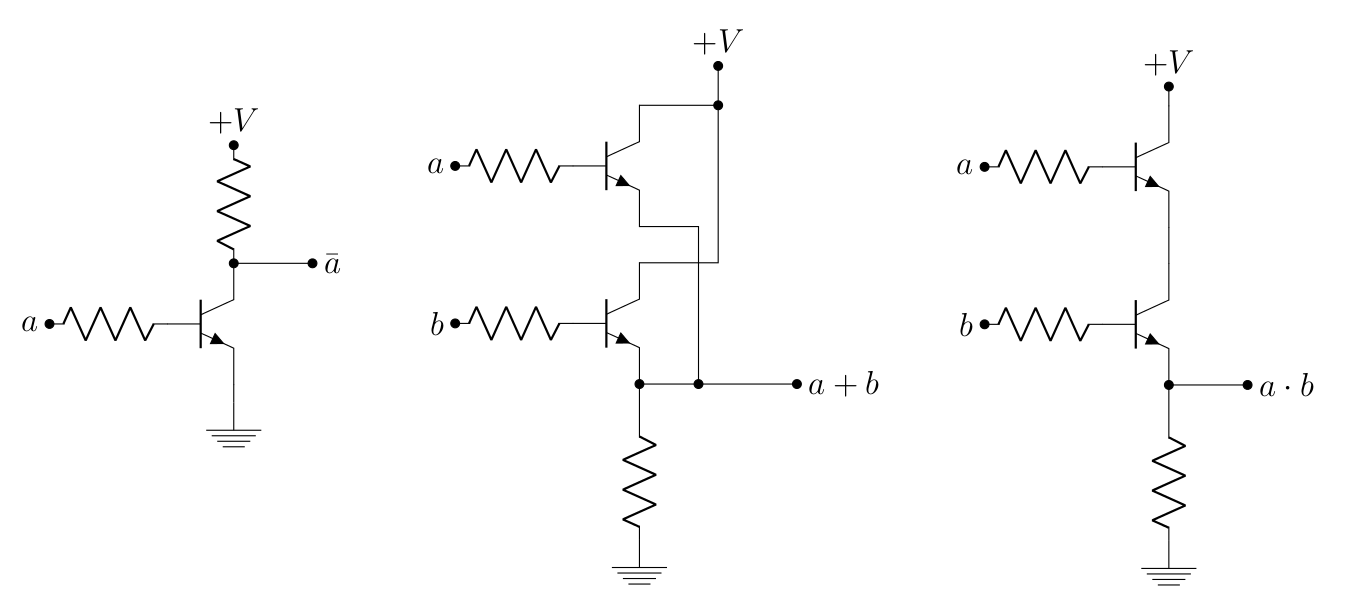
Si vous avez bien intégré que le transistor fonctionne à peu près comme un interrupteur dont le potentiel sur la base déterminerait l’état ouvert ou fermé, vous devriez normalement ne pas avoir trop de difficulté à comprendre ses schémas. Ainsi, si on prend par exemple le cas de la négation, si on applique pas de tension sur (ce qui correspond à « faux »), l’interrupteur est alors « ouvert » et alors la sortie sera à une tension de , soit « vrai ». À l’inverse, si on applique une tension sur , l’interrupteur est « fermé », et le potentiel en sortie est alors nul (la terre est par définition à 0 volt). C’est bien le principe de la négation (ou de ce que les Anglais appellent parfois inverter).
Le même principe d’interrupteur s’applique pour les schémas associés à ET et OU, qui reviennent alors à ce qu’on avait montré au début de ce chapitre, vu que c’est la tension appliquée à la base (donc les entrées et ) qui déterminent l’ouverture de l’interrupteur ou pas.
En pratique, ces composants sont plus gourmands en énergie (et dissipent plus de chaleur) que leurs équivalent à effet de champ, même si plus rapides. À l’heure où on aimerait bien qu’un portable tienne plus d’une heure, c’est bel et bien ces derniers qui sont utilisés la plupart du temps.
MOS (metal-oxyde-semiconductor), FET (field-effect transistor) et CMOS (complementary MOS)
Le concept d’un interrupteur dont l’ouverture et la fermeture est commandée par la tension appliquée à la base étant quand même vraiment intéressant, à peu près à la même époque a été imaginée la technologique dite des transistors à effet de champ4. L’effet est en pratique similaire, mais la mise en oeuvre est légèrement différente.
Pour ça, il faut explorer un autre effet, celui qu’on trouve en fait dans un autre élément de circuit classique, les condensateurs. Un condensateur est formé de deux plaques de métal, séparées d’un isolant électrique. Lorsqu’on applique un potentiel, disons positif, sur une des faces du condensateur, on génère des charges négatives sur l’autre plaque, générant de ce fait un champ électrique entre les deux plaques du condensateur.
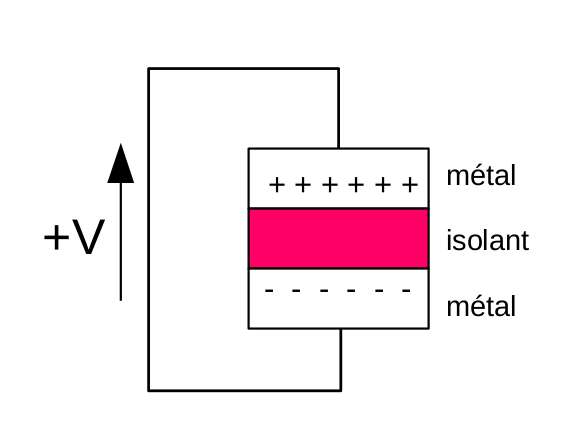
Or, cet effet peut être utilisé de manière intéressante si on construit le bon montage. Voici comment on réalise un transistor à effet de champ (FET).
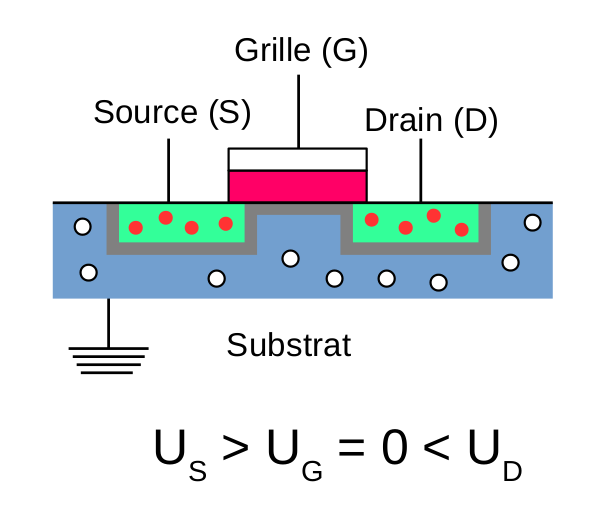
Tout comme le transistor bipolaire NPN, on retrouve ici le mélange des deux types de semi-conducteurs. Ici, on a un transistor dit « nMOS », car ce sont des semi-conducteurs de type n qui vont fournir les charges. Le terme MOS provient du fait qu’on utilise un oxyde métallique (metal oxyde) comme isolant entre la couche de métal et le semi-conducteur p, afin de former la grille (G, gate en anglais, qui signifie alors « porte »). Les deux semi-conducteurs n sont ici appelés la source (S) et le drain (D, to drain signifiant en anglais « vider » ou « vidanger »), tandis que le semi-conducteur p est appelé le substrat.
On voit qu’on s’arrange pour placer les jonctions pn en polarisation inverse, en plaçant un potentiel positif sur la source et le drain, tandis que le substrat est placé à la terre (0 volt). Dans cette configuration, aucun courant ne circule donc entre la source et le drain. Mais cette fois-ci, le rôle de la grille ne va pas être de placer une jonction en polarisation directe ! Appliquer un potentiel sur celle-ci va plutôt créer des charges négatives dans la jonction entre l’oxyde (rose sur le schéma) et le substrat, induisant un champ électrique (d’où le terme FET, field induced transistor) qui va alors s’opposer aux porteurs de charges minoritaires du substrat, créant de ce fait un « canal » de conduction où les électrons de la source peuvent alors se promener librement vers le drain. En d’autres termes, le courant passe !
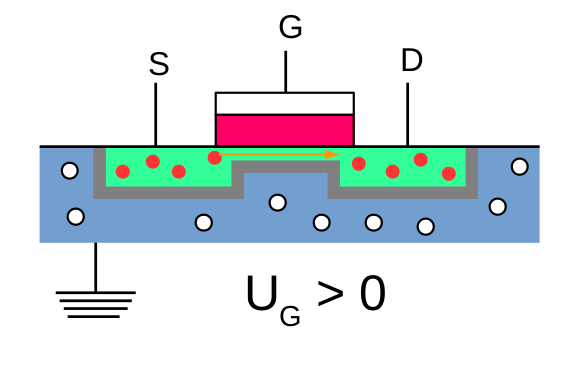
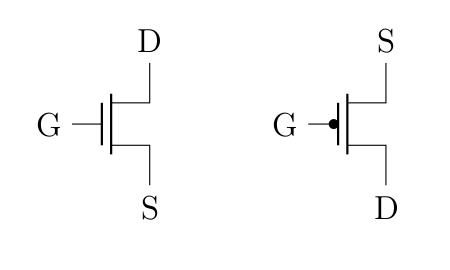
Il est évident que ce type de transistor permet de réaliser le même genre de circuit que ceux présentés pour la jonction npn (voir par exemple ici). Les représentations de ces deux transistors sont les suivantes.
En soi, rien de neuf sous le soleil, il s’agit toujours d’un transistor qui s’active quand on lui applique un potentiel. Mais qu’est ce qui se passe lorsqu’on met des nMOS et pMOS ensemble ? Observons par exemple le schéma suivant.
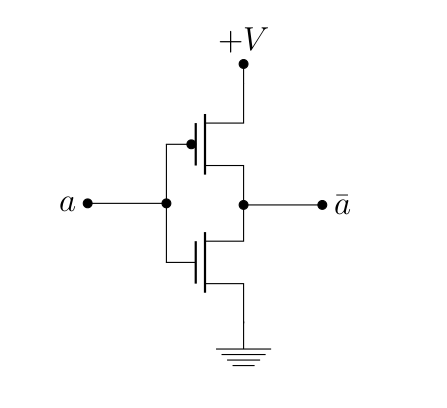
Pourquoi est-ce intéressant ? Parce que si on applique pas de tension sur , alors c’est le pMOS qui laisse passer le courant (on vient de voir que le nMOS était alors bloquant), donc la sortie est a (« vrai »). À l’inverse, à l’application d’une tension sur , c’est le nMOS qui laisse passer le courant, ce qui place la sortie à un potentiel nul (« faux »). C’est ce qu’on appelle un circuit CMOS, le « C » étant pour complémentaire (puisqu’on utilise une paire de pMOS et de nMOS).
Le gros avantage de cette manière de fonctionner, c’est que et la terre ne sont jamais en contact. En effet, dans les montages impliquant des transistors bipolaires, l’ouverture de ceux-ci finissait toujours par mettre en contact le pôle positif et négatif, ce qui consomme de l’énergie. Là, ce n’est jamais le cas.5 C’est pour cela qu’on a finalement favorisé ce genre d’architecture et que les CMOS sont aujourd’hui utilisés dans les CPU et les mémoires (voir chapitre suivant).
En se grattant un peu la tête, on se rend compte qu’un cMOS correspond à une porte logique de type NOR.
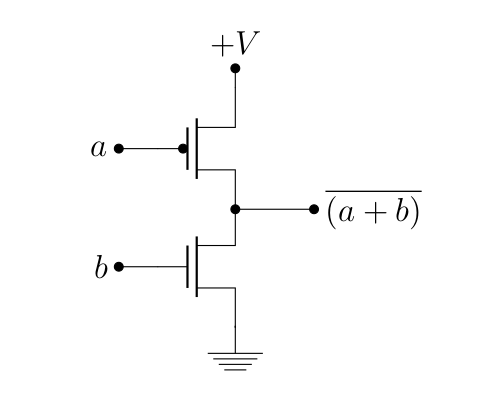
Pour preuve, voici la table de vérité du CMOS, exprimé en termes de potentiel.
| sortie CMOS | ||
|---|---|---|
| 0 | 0 | |
| 0 | 0 (et énergie perdue) | |
| 0 | 0 | |
| 0 |
Et revoici la table de vérité du NOR.
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
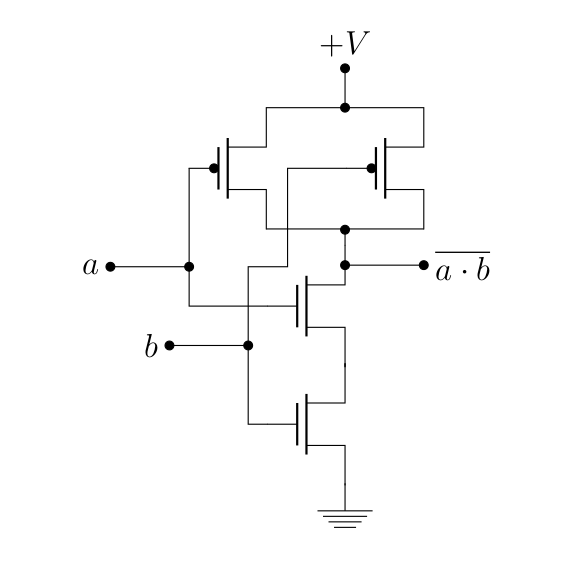
On voit bien que ça correspond. Dès lors, l’exercice revient à exprimer un circuit logique en termes de portes NOR. Par exemple, voici une implémentation pour NAND.
- À priori et puisque la vitesse de diffusion des électrons est plus importante que celle des trous, c’est la jonction NPN qui est préférée.↩
- En anglais, « bipolar junction transistor », ou plus simplement BJT.↩
- Et même si ça ne nous intéresse pas ici, d’amplificateur, car ce type de jonction est créée de telle manière à ce que le courant collecté réagisse en fonction du courant appliqué à la base, mais avec un facteur 100 ou 1000, par exemple. Vu que les MOSFET sont préférés dans les portes logiques, c’est dans les amplificateurs qu’on retrouve ces transistors.↩
- Les transistors à effet de champs (principe breveté en 1925, CMOS breveté en 1936) sont même une invention antérieure aux transistors bipolaires (1947 et 1948, aux laboratoires Bell). Sauf que ni l’un, ni l’autre n’étaient facile à mettre en œuvre industriellement. ↩
- … Sauf quand les deux MOS sont en train de changer de sens, là, on a une perte d’énergie, puisqu’il arrive un bref moment où les deux dispositifs sont passants. Du coup, si on change régulièrement d’état, on consomme d’autant plus d’électricité. Il y a tout de même moyen de contrôler ce phénomène (en), mais jamais en dessous d’une certaine limite.↩
Des portes, des portes et des portes !
Bon, en pratique, tout ce qui vient avant n’est pas réellement nécessaire. Tout ce qu’il est important de savoir (sauf si vous voulez réaliser un circuit ayant une application commerciale réelle), c’est qu’il est possible de réaliser des circuits logiques. Pour la suite, on va donc ranger sous le tapis ces histoires de potentiel et de semi-conducteurs pour se concentrer sur les circuits eux-mêmes. Pour ça, on a besoin de composants logiques, qu’on va nommer portes logiques (ou, plus simplement, porte). Voici les 3 portes de bases :

À ça, on rajoute 3 portes qu’on a déjà rencontré dans le premier chapitre et qui se retrouvent dans certains circuits1 (même si le processus de simplification de Karnaugh ne permet pas de les faire apparaître).
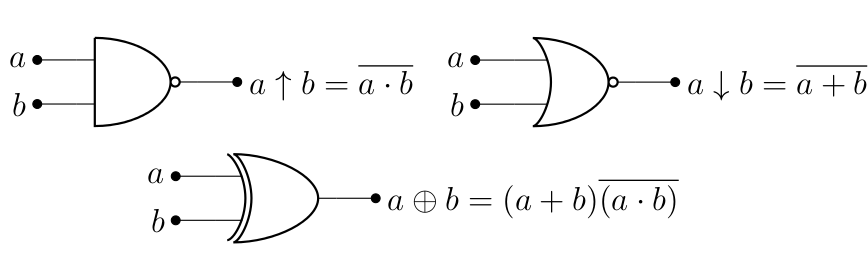
Ce qu’il est important de savoir, c’est que passer au travers d’une porte demande du temps. Bien entendu, on ne parle pas d’un temps mesuré en seconde, mais à l’échelle de la fréquence d’un processeur (qui se mesure en MHz, donc en millions d’instructions à la seconde), ça devient limitant, ce qui signifie qu’il faut que le nombre de porte par lesquelles voyage un signal devrait être le plus réduit possible, légitimant alors le procédé de simplification vu plus haut (de plus, ça rend les circuits électriques plus lisibles).
Ainsi, si on reprend l’exemple du chapitre précédent, on avait
Voici tout d’abord le circuit correspondant à la forme disjonctive.
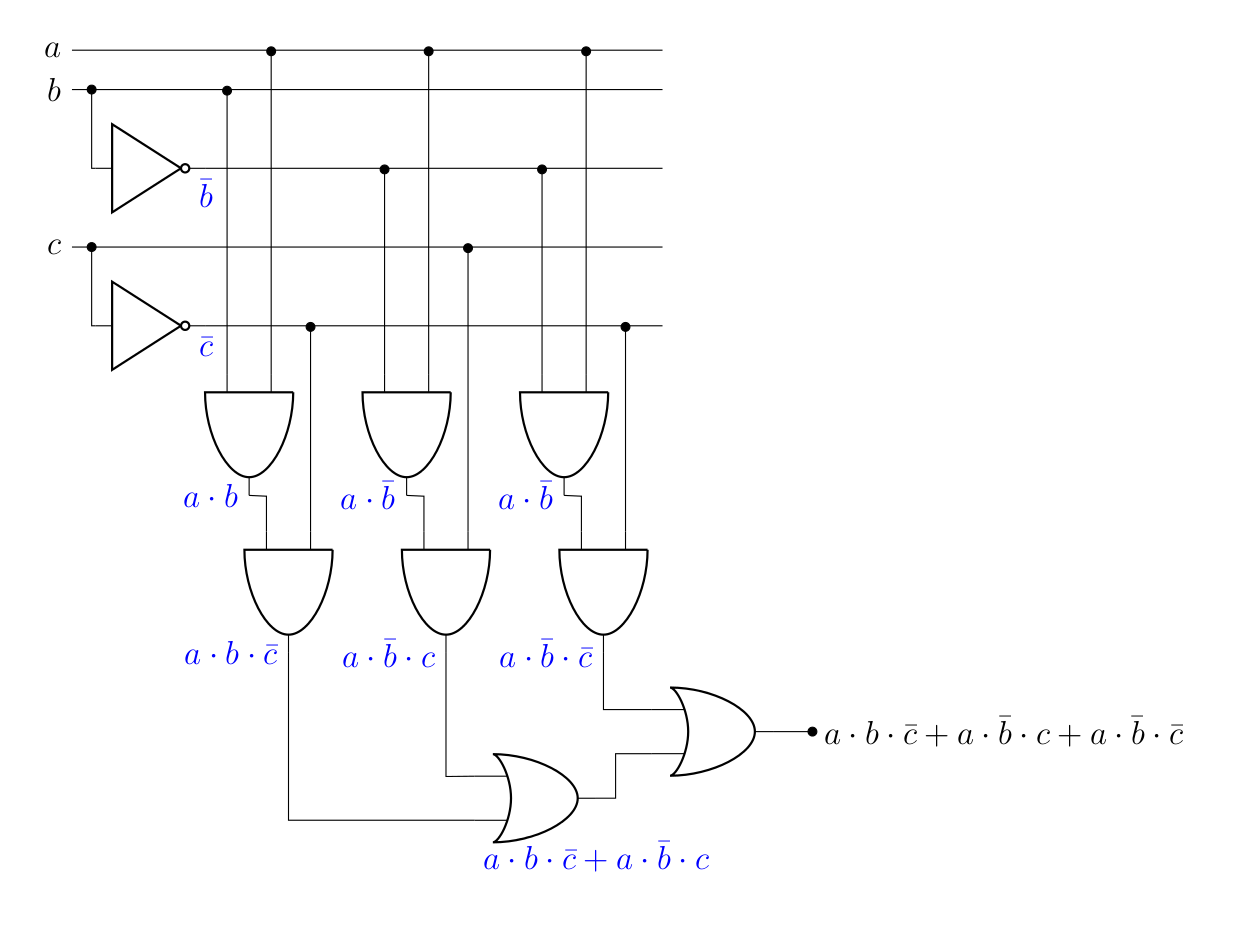
C’est long, mais assez systématique :
- Pour chaque variable, on « tend un câble » pour celle-ci et sa négation, si c’est nécessaire (ici, n’est pas nécessaire).
- On construit ensuite les termes conjonctifs (pour rappel, c’est aussi ce qu’on appelle les minterms, ) en utilisant les portes « ET ».
- Puis finalement, on crée les disjonctions () en rassemblant les conjonctions à l’aide de portes « OU ».
Si vous comptez, vous verrez que chaque signal passe en moyenne par 4 portes (5 dans le pire des cas, 3 dans le meilleur des cas). Si on compare maintenant à la version disjonctive simplifiée, construite selon le même principe…
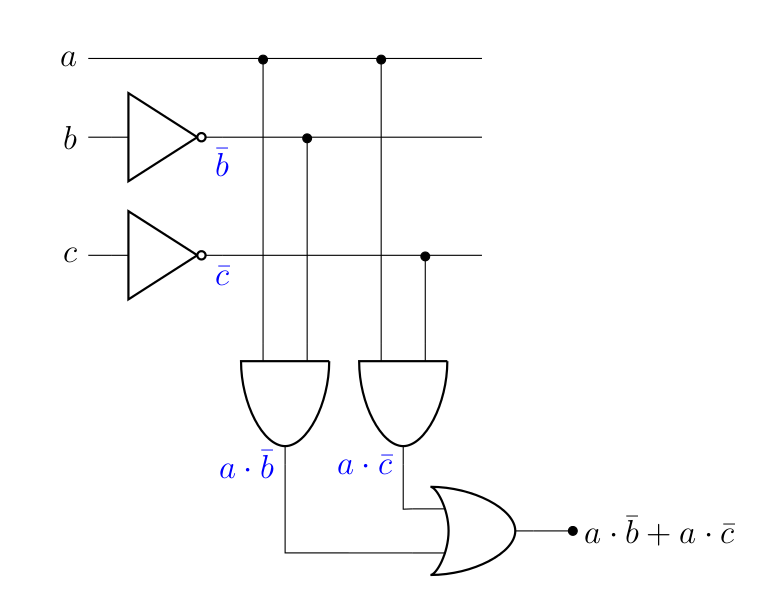
…On constate que le signal passe cette fois en moyenne par 3 portes (2 dans le meilleur des cas), donc un gain d’au moins une porte. Par ailleurs, le nombre total de portes nécessaire pour implémenter le circuit passe de 10 à 5, soit une réduction de moitié. Très clairement, la simplification est intéressante dans ce cas et d’ailleurs dans la plupart des cas.
Néanmoins, il est possible d’obtenir une version de ce circuit qui n’utilise que 4 portes en dessinant la forme conjonctive. Saurez-vous le dessiner ?
La forme normale conjonctive demande en effet 4 portes pour être implémentée :
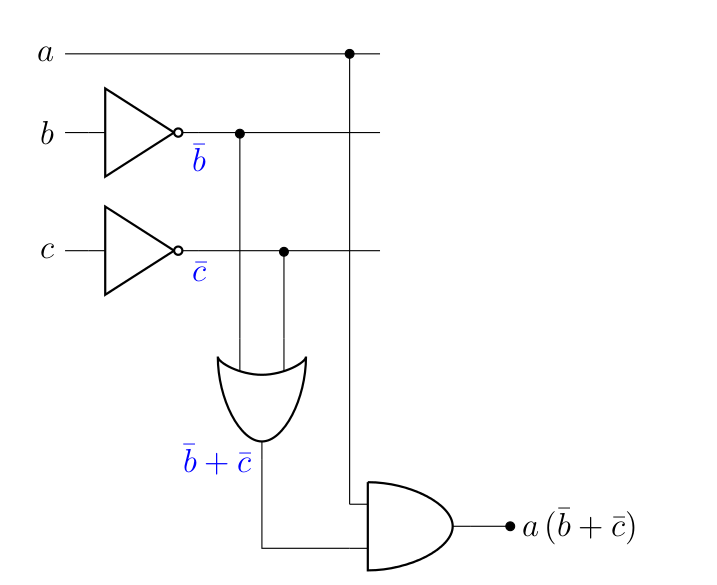
Bien entendu, la forme conjonctive n’est pas forcément plus courte que la disjonctive et il faut tester les deux pour le savoir (ou, avec un peu d’entraînement, compter directement dans l’expression de base).
Et si on s’autorise l’utilisation des fameuses « portes logiques secondaires », il est encore possible d’obtenir quelque chose de plus simple.
Il suffit de partir de la version conjonctive et d’utiliser une porte NAND (« NON ET »). En effet, la loi de De Morgan énonce que , ce qui est bien le terme disjonctif rencontré dans l’expression précédente. On obtient alors :
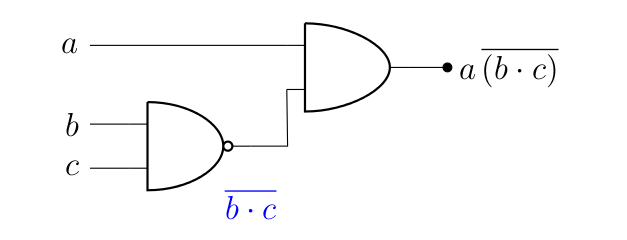
On voit donc ici que la simplification de Karnaugh est un outil intéressant, même s’il est parfois possible d’aller au-delà.
- Il est même possible d’implémenter toutes les autres portes avec juste une porte NAND ou NOR. Par exemple, le système de guidage d’Apollo (utilisé par la mission Apollo 11) était construit uniquement avec des NOR.↩
Au final, ce qu’il est réellement important de retenir de ce chapitre, c’est sa fin, à savoir :
- Il existe des symboles pour les 3 opérations logiques de bases, c’est-à-dire la négation, ET et OU.
- La simplification de Karnaugh, vu au chapitre précédent, permet de réduire drastiquement le nombre de portes à utiliser pour implémenter un circuit logique (même s’il est possible d’aller plus loin grâce aux portes NAND, NOR ou XOR).
Nous sommes à la moitié du parcours ! Dans le prochain chapitre, on verra comment il est possible de représenter des nombres afin de les manipuler dans des circuits logiques, donc ce qui se cache derrière la représentation binaire.