Armé de toutes ces connaissances, il est finalement temps de terminer notre voyage avec un petit aperçu de quelques circuits présents dans les processeurs modernes.
Multiplexeurs et démultiplexeurs
Multiplexeur (MUX)
Premier élément d’électronique utile pour la suite, le multiplexeur : plusieurs entrées, un sélecteur et une sortie. En fonction de la valeur du sélecteur, c’est une des entrées qui apparaît en sortie. Ainsi, on numérote les entrées et on donne au sélecteur la valeur de l’entrée qu’on veut voir en sortie.
Par exemple, prenons un multiplexeur simple, dit 2 vers 1 : on a deux entrées, et (pouvant chacune valoir 0 ou 1), un sélecteur, (valant 0 pour la sélection de , 1 pour ) et une sortie (dont la valeur dépend de l’entrée sélectionnée et de la valeur de cette entrée).
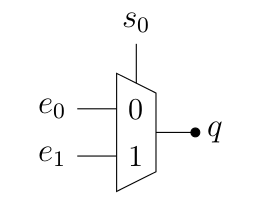
À quoi ressemble le circuit électrique correspondant à cet élément ? Pour le savoir, vous pouvez constater qu’on a ici 3 entrées et une sortie. Il s’agit donc d’une fonction booléenne de type . Le reste, c’est la création d’une table de vérité, puis la simplification par Karnaugh, comme on l’a vu ici. Vous essayez ?
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Vous devriez assez facilement tomber sur , ce qui est assez logique. Le circuit associé est donc:
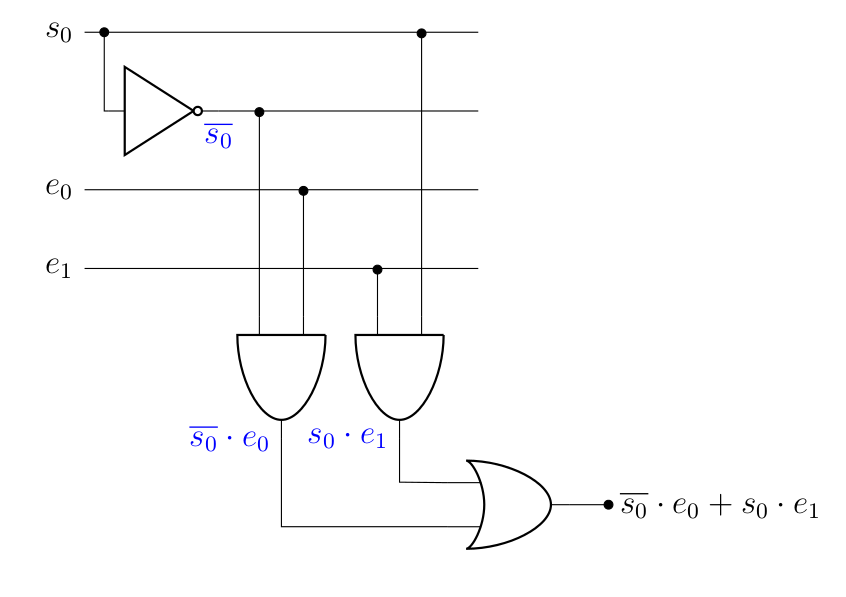
Évidement, il existe des multiplexeurs 4 vers 1, 8 vers 1, 4 vers 2, etc. Néanmoins, le nombre de bits de sélection augmente avec le nombre d’entrée (4 entrées nécessitent 2 bits de sélections, 8 entrées nécessitent 3 bits de sélection, et ainsi de suite). Bien que ce soit ensuite un peu moins marrant à traiter avec Karnaugh, il est tout à fait possible d’arriver à des simplifications (en utilisant directement les règles de l’algèbre booléenne). Une autre manière de faire est de chaîner les multiplexeurs. Voici un exemple de multiplexeur 4 vers 1 réalisé à partir de multiplexeurs 2 vers 1.
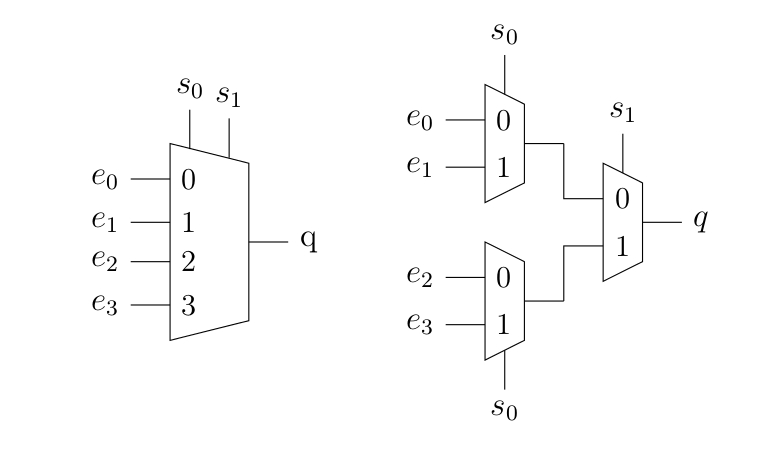
Ces composants sont très utiles pour piloter un composant électronique. En effet, comme on le verra ci-dessous, il permet de choisir entre différentes entrées en fonction de l’opération à réaliser.
Démultiplexeur (DEMUX)
À l’inverse, le démultiplexeur prend une entrée et la redirige vers la bonne sortie en fonction du sélecteur, ce qui donne l’équivalent électronique de l’aiguillage.
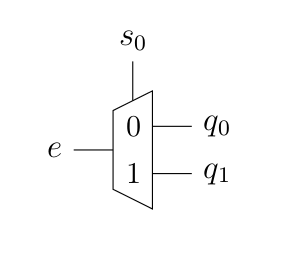
Cette fois, la fonction logique sera une série de « ET ». En effet, pour être active, une sortie donnée devra correspondre au sélecteur. Par exemple, dans le démultiplexeur donné plus haut, la fonction correspondante à la sortie « 0 » serait tandis que . Dès lors, à quoi ressemblera le circuit logique ?
Sachant cela :
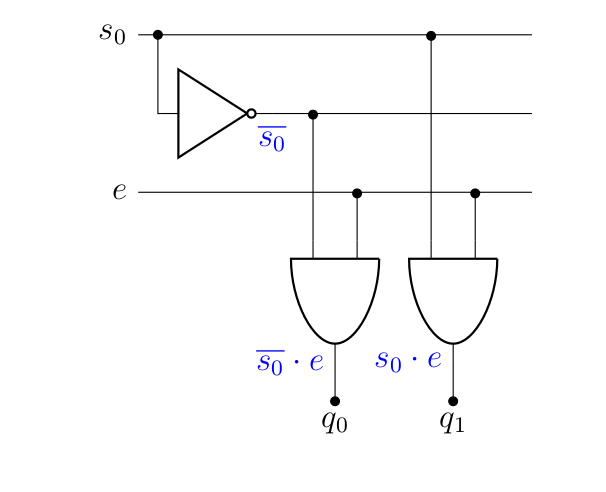
Bien entendu, il existe des démultiplexeurs 1 vers 4, 8…
Couplés aux multiplexeurs, ces composés permettent de transmettre différentes informations par le même canal.
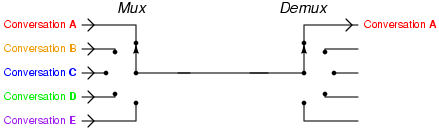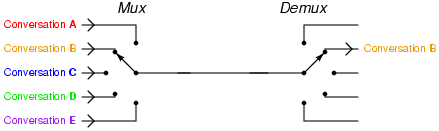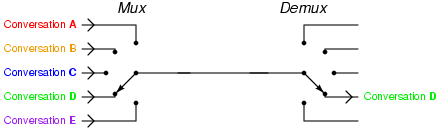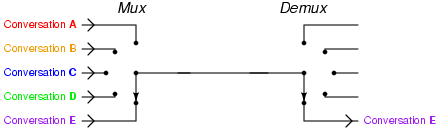
Unité arithmétique et logique (ALU)
Bon, maintenant qu’on a vu les (dé)multiplexeur, on peut s’attaquer à un composant de base d’un processeur, c’est l’ALU, pour arithmetic logic unit (unité arithmétique et logique, en bon français). Dans un processeur, c’est ce type de circuit qui réalise toutes les opérations de base.
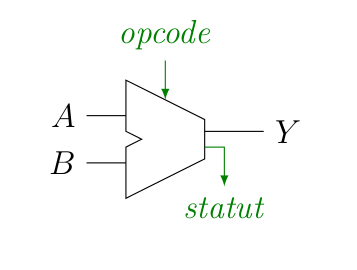
Une ALU prend un certain nombre de choses en entrée : deux mots, représentant des entiers et dont le nombre de bit dépend du processeur (32 ou 64 bits), et , ainsi que l’opération à réaliser par l’ALU, l'opcode (pour operation code). On retrouve alors le résultat de l’opération en sortie, (mot d’autant de bits que les entrées), ainsi qu’un certain nombre d’informations, regroupées sous le terme de statut (par exemple, pour citer quelque chose qu’on a déjà rencontré, l'overflow, mais aussi d’autres choses intéressantes).
En fonction de l’ALU, on peut réaliser un certain nombre d’opérations sur les entrées et , telles que :
- Les mathématiques de base : addition, soustraction, complément à 2, éventuellement les multiplications et divisions, …
- Les opérations logiques: « ET », « OU », …
- Les comparaisons: , , …
D’autres opérations sont parfois disponibles dans des ALU spécialisées, telles que le calcul flottant (nombres à virgule), les décalages et rotations de bits, des opérations mathématiques plus complexes (racines carrées, exponentielle, logarithme et autres joyeusetés), mais le principe reste le même. Évidement, plus on rajoute d’opérations, plus les circuits associés sont complexes, le but ne va donc pas être ici de les passer en revue. Néanmoins, on va voir deux ou trois morceaux intéressants.
L’additionneur binaire
On avait fini le chapitre précédent en montrant qu’on pouvait implémenter les 5 opérations mathématiques de base à l’aide de l’addition et de quelques astuces. Il nous faut donc un circuit permettant de réaliser l’addition de 2 bits en position de et , qu’on va noter et , mais en gérant le report entrant, noté , et pour stocker le tout dans le bit de , noté , et en calculant s’il est nécessaire d’avoir un report sortant, , pour la prochaine opération. Autrement dit, on est face à la table de vérité ci-dessous.
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Il n’y a plus qu’à regarder quelles fonctions logiques on obtient alors.
- Pour ce qui est du résultat de l’addition, , ce qui n’est pas simplifiable en utilisant Karnaugh (parce que ça donne un magnifique damier). Néanmoins, si on fait intervenir la porte XOR, , on peut obtenir une simplification en termes de nombre de portes logiques. Ainsi, cela revient à . Vous pouvez même le vérifier par vous-mêmes1.
- Pour le report sortant, on obtient cette fois quelque chose de simplifiable par Karnaugh. Une fois que c’est fait, on se rend compte que (on gagne une porte en mettant en évidence).
Ne reste plus qu’à faire le circuit correspondant, ce que je vous laisse essayer :
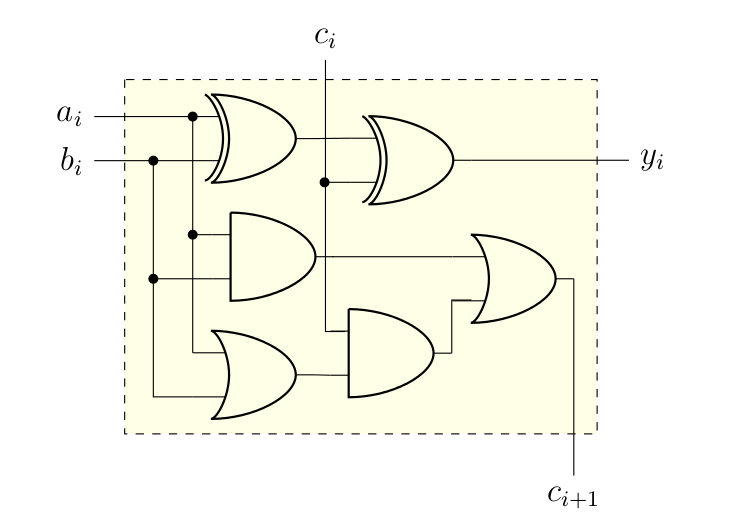
Pour la suite, on va simplifier les choses en représentant l’additionneur binaire comme suit :
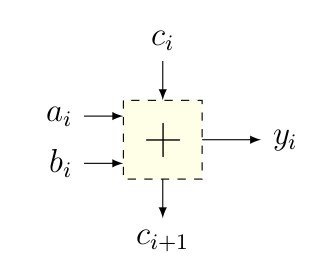
Une petite ALU 1 bit
On entre clairement dans le domaine du spéculatif : peu de chance qu’un vrai circuit de processeur ressemble à ceux que je vais vous présenter. Mais conceptuellement, ça tient la route.
Jusqu’ici, on peut juste réaliser l’addition. Qu’à cela ne tienne, on a vu que pour réaliser la soustraction, , il suffisait de placer à 1, et d’additionner avec . On a donc besoin d’un signal, qu’on va appeller , qui donne si et si autrement dit, . Et le circuit permettant de réaliser la soustraction est donc simplement le suivant.
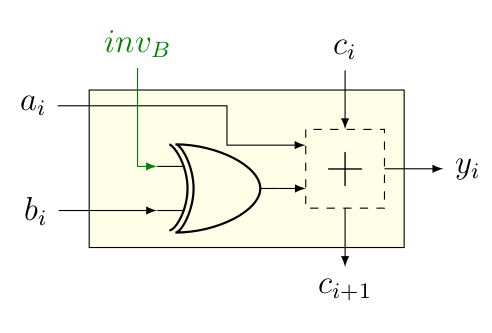
Bon, on aimerait aussi que notre ALU face un peu plus que l’addition et la soustraction, par exemple qu’elle face aussi le « ET » et le « OU ». Néanmoins, pour faire ça, on va avoir besoin d’un multiplexeur qui réalise le choix entre les différentes opérations à réaliser par l’ALU, qu’on va commander par le signal op. Tant qu’on est dedans, on va rajouter un signal qui va permettre d’obtenir « NON ET » (comme ) et « NON OU » (comme ). Et l’histoire de préparer la suite, on va également rajouter une entrée , dont vous allez comprendre l’intérêt un peu plus bas.
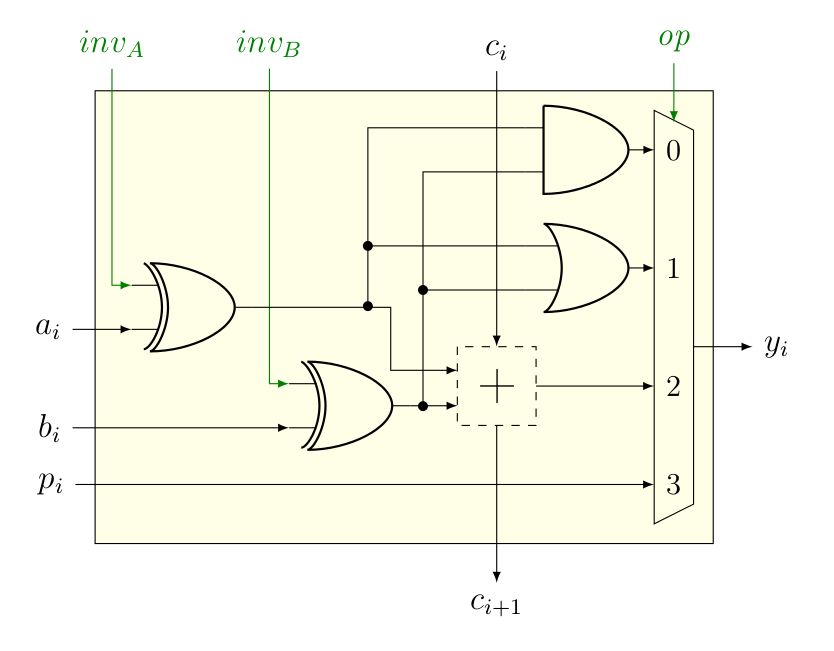
Pour la suite, on va encore dézoomer d’un cran et représenter ce type d’ALU de la manière suivante.
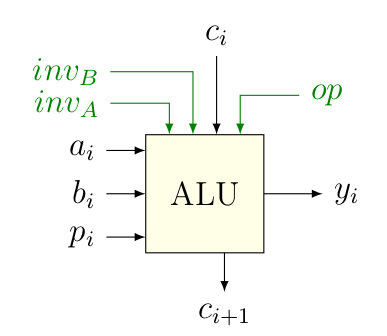
Une « petite » ALU bits
Maitenant qu’on a une ALU 1 bit, on peut l’utiliser pour faire des calculs sur des nombres représentés sur plusieurs bits. Combien ? Comme ça a été dit dans le chapitre précédent, ça dépend du processeur, mais généralement 32 ou 64 bits, qui est la taille de la représentation des nombres entiers. De manière assez logique2, une telle ALU sera alors formée de ALU 1 bit mises bout à bout pour traiter chacun des bits de et de . Dès lors, on peut créer notre ALU comme suit.
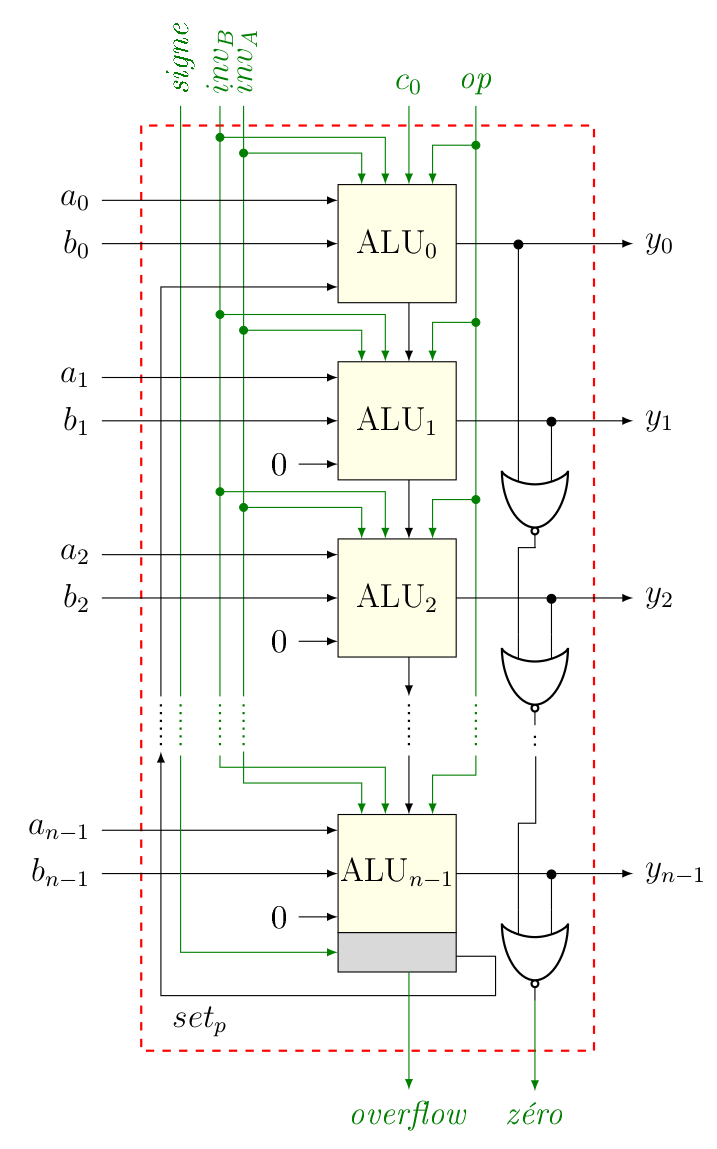
Donc, qu’est-ce qu’on a là ? Vous devez reconnaître le centre : c’est là que se font les différentes opérations, bit par bit, comme promis. Pour que ça fonctionne, il faut évidement donner à chacune de ces ALUs les différents signaux op, et .
Par contre, deux modifications ont été apportées afin que cette ALU soit capable de faire les comparaisons :
- La première, c’est pour réaliser la comparaison . Pour ça, l’astuce est de calculer , puisque si est égal à , le résultat sera de… zéro. Ensuite, pour vérifier que c’est bien le cas, on fait passer le résultat de chaque soustraction bit à bit dans des portes « NON OU « (à droite dans le schéma). En effet, (voir le premier chapitre). Le résultat, c’est le signal zéro, qui vaut donc 1 si , c’est-à-dire que .
- La deuxième, basée sur la même astuce, c’est pour réaliser les comparaisons du type . En effet, si , est un nombre négatif. À l’inverse si , est un nombre positif. Or on a vu que si un nombre était négatif, son bit en première position (le bit de poids fort) valait 1. C’est à ça que va servir la fameuse sortie qu’on a rajoutée plus haut. Si cette sortie est sélectionnée, tous les bits seront mis à zéro, sauf le premier, dont la valeur sera égale au bit de poids fort résultant de la soustraction de et ( dans le schéma), ce qui explique en partie pourquoi l’ALUn-1 est différente des autres (la partie « grise » contient quelques circuits supplémentaires pour gérer cela3). Autrement dit, si , , sinon. Dans certains processeurs, c’est également un signal, comme zéro. À noter que le calcul dépend de si on compare des nombres signés ou pas (d’où le signal supplémentaire signe).
Et finalement, la dernière modification apportée est là pour permettre la détection de l'overflow, comme expliqué dans le chapitre précédent. Pour cela, il est nécessaire de connaître le report entrant et sortant ( et ), ainsi que le fait qu’on travaille avec des nombres signés ou non. De même, c’est l’ALUn-1 qui a été modifiée de manière à indiquer s’il y a dépassement ou non.
Et on a donc une ALU qui est capable de faire des opérations sur les nombres entiers signés ou pas, y compris des comparaisons. C’est rudimentaire, mais vous n’imaginez pas tout ce qu’on peut déjà faire avec ça.
Tout ça n’est toutefois pas très efficace. En effet, tout ça est très joli sur le papier, mais j’ai volontairement fait en sorte de ne pas complexifier la chose en omettant des aspects très importants qui reposent sur la petite note faite il y a deux chapitres : passer par une porte prend du temps ! Deux conséquences à cela :
-
On a créé des scénarios de course (race condition, que les développeurs parmi vous connaissent peut-être déjà, parce que ce n’est pas limité à l’électronique). Par exemple :
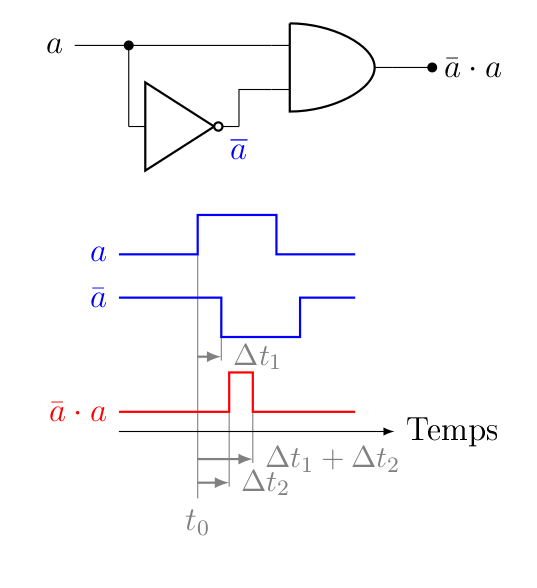
Scénario de course simple entre deux composants électroniques (inspiré de Wikipédia). On verra plus loin que ce scénario a ceci dit un intérêt. Imaginons qu’on change la valeur de . Le passage par la porte « NON » implique un délai de temps, par rapport à la première entrée de la porte « ET », ce qui signifie que la valeur de sortie de cette porte « ET » n’est correcte qu’après un temps équivalent à (le passage par la porte « ET » impliquant un second délai ). Autrement dit, comme les changements ne sont pas instantanés, il faut attendre un certain temps pour que le système se « stabilise » avant de lire une valeur correcte. Pire, durant l’intervalle, la valeur en sortie de la porte « ET » est incorrecte. Il faut donc attendre un certain temps…
Pour ceux que ça intéresse, ça se traite généralement en ajoutant de la redondance et/ou en simplifiant le circuit (comme c’est le cas ici).
-
La création d’un circuit comme celui présenté plus haut où les unités sont mises à la chaîne induit un énorme problème généré par le calcul du report. En effet, le calcul du dernier reste () requiert de passer par rien de moins que portes, sans compter le temps qu’il faut pour réaliser les opérations à la suite : le calcul de requiert le calcul de , qui requiert le calcul de , qui requiert celui de , qui… rends le temps très long ! Ça impacte donc le nombre d’opération qu’on peut réaliser par seconde, et ce n’est pas quelque chose de souhaitable. Il existe cependant des solutions, par exemple le carry lookahead adder (« additionneur à retenue/report anticipée »), une alternative assez intelligente pour régler le problème du report et qui est une fois encore une application assez jolie de l’algèbre de Boole.
Bonus : et ainsi, on en arrive presque à l’assembleur
Si on résume, on a besoin de différents bits de contrôle nous permettant de réaliser tout un tas d’opérations. Et c’est là qu’intervient l’Assembleur. C’est quoi? C’est le langage de « programmation » le plus proche du pour communiquer avec le processeur. Ainsi, les instructions en Assembleur sont directement lues et interprétées par le CPU, qui va agir en fonction. Une instruction Assembleur contient un opcode (qui dit au CPU quoi faire) et des opérandes (qui dit au CPU quoi utiliser pour le faire). Évidement, cet opcode n’est pas un mot, mais un nombre en binaire, qui peut alors être passé à la moulinette de portes logiques pour déterminer de quelle opération il s’agit. Ainsi, dans un CPU, il ne serait pas illogique de retrouver sous une forme ou une autre dans cet opcode les différentes valeurs de , , et .
Le processeur trouve les données qu’il manipule dans des registres : il s’agit de zones mémoires très petites (typiquement, 1 mot) et à accès très rapide (à l’échelle du processeur). Quand on manipule une variable dans un langage de programmation, elle est en pratique copiée dans un registre avant d’être manipulée. Il existe, en fonction de l’architecture du processeur, un nombre de registre différent, mais ce nombre est en fait très faible comparé aux nombres de variables que peut manipuler un programme.
Prenons par exemple le MIPS32 (en) (un certain type de processeur, aujourd’hui plus scolaire qu’encore utilisé), on voit que les instructions processeurs sont séparées en différents « champs ».
Instruction MIPS (32 bits) | |||||
Opcode (6 bits) | rs (5 bits) | rt (5 bits) | rd (5 bits) | shamt (5 bits) | func (6 bits) |
Pour les opérations mathématiques, l’opcode est le même. Le function code (func) contient les différents bits de contrôle pour l’ALU. rs, rt et rd (registres source, target et destination) sont les registres que l’instruction doit manipuler (en MIPS, il y a 32 registres, d’où le code sur 5 bits qui représente le numéro du registre). Le shift amount (shamt) est utile pour les opérations de décalage de bits. Typiquement, pour l’instruction add et sub (qui font, comme leur nom l’indique, l’addition et la soustraction de rs et rt pour inscrire le résultat dans rd), l’opcode vaut dans les deux cas, tandis que le function code vaut () et (), respectivement (pour les additions et soustractions non-signées, les function codes valent et , de manière logique).
Le monde de l’Assembleur nécessiterait cependant un tutoriel à lui tout seul. En effet, les instructions sont spécifiques à un type de processeur (ARM ou intel, par exemple) et certaines subtilités existent (par exemple au niveau des registres). Néanmoins, le principe de base reste le même.
La mémoire (et l'horloge)
C’est quoi de la mémoire, en fait ? D’un point de vue tout à fait théorique, ce n’est jamais qu’une grosse fonction booléenne, pour laquelle la variable d’entrée est l’adresse, et la sortie est la valeur du bit situé à l’adresse demandée1 (c’est le concept table de correspondance, look-up table (en), abrégé LUT).
Évidement, vous connaissez des éléments qui constituent « de la mémoire » pour un ordinateur. De tête, on pourrait probablement citer les CD/DVD/Blue Ray, les clés USB et autres cartes flash, les disques durs et SSD, ou encore la fameuse RAM (Random-Access Memory). Là-dedans, on peut quand même distinguer :
- La mémoire volatile et non-volatile. La mémoire volatile disparaît en l’absence d’alimentation électrique (c’est le cas de la RAM), la mémoire non-volatile existe indépendamment de l’alimentation (c’est le cas de tout les autres composants cités).
- La mémoire à accès séquentiels ou aléatoire (random). Une mémoire à accès aléatoire permet, en un temps rapide, d’accéder à un endroit précis, là ou une mémoire à accès séquentiels… Le permet, mais en un temps plus long. Un exemple typique du dernier cas sont les bandes magnétiques (oui, les cassettes audio, mais ça a longtemps servi comme support de sauvegarde pour les ordinateurs aussi, des programmes étaient même vendus comme ça). On se rend également compte que le terme « RAM » n’est absolument pas précis, puisqu’on pense aux barrettes mémoires de notre ordi, alors que le terme s’applique en fait très bien à un disque dur (qui permet aussi d’accéder à un endroit arbitraire en un temps court). Le terme exact pour les barrettes de RAM est en fait DRAM (dynamic random-access memory) (voir de la SDRAM si on veut pinailler sur les détails), comme on aura l’occasion de le voir plus loin.
- La manière de stocker les bits varie également d’un support à un autre. En ce qui concerne les disques optiques (45 tours, CD, DVD), il s’agit bien entendu de creux et de bosses. Le disque dur exploite lui les propriétés magnétiques de métaux (c’était également le cas des disquettes et de la bande magnétique, qui se base sur les propriétés magnétiques de l’oxyde de fer, plus communément appelé la rouille, d’où la couleur des bandes magnétiques d’ailleurs). Quant aux autres types de mémoire, on aura l’occasion d’en parler.
ROM ?
Avant de parler de mémoire volatile, passons un instant sur les ROM (read only memory). On leur donne aussi le petit nom de mémoire morte en français. Il s’agit simplement d’un circuit implémentant la fameuse fonction booléenne qui, pour une adresse entrée (dans les word lines), donne la valeur des bits en sortie (dans les bit lines), les unes et les autres étant reliés par ce qu’il faut de porte logique pour obtenir la fonction booléenne. Dans une version naïve, ces fonctions peuvent être implémentées simplement à l’aide de multiplexeurs, mais ça en ferait vite beaucoup. Une autre idée, c’est d’être plus systématique et en accord avec ce qu’on a vu dans le chapitre sur la logique booléenne : une fonction booléenne, c’est une disjonction de minterms (qui sont des conjonctions de littéraux, pour rappel). Du coup, on peut schématiser les choses comme suit.
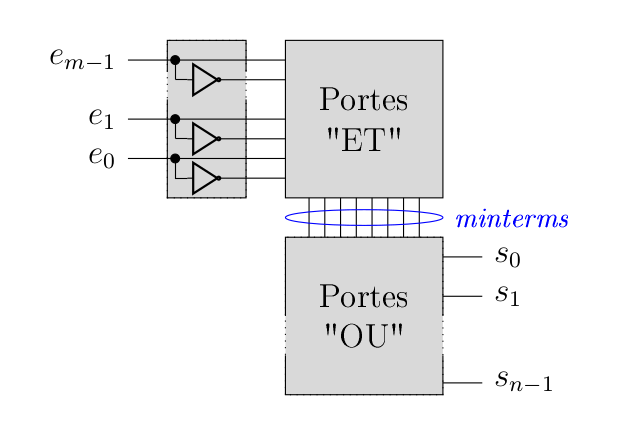
Écrire une ROM demande donc de créer un circuit logique (c’est là que l’algorithme de Mc-Cluskey prend tout son sens, afin de demander à un ordinateur de faire le travail de simplification). Pour rendre ça un peu plus systématique, on a inventé des ROM « programmables » (les PROMS). L’idée de base, c’est un array de portes « ET », suivis d’un array de portes « OU », et par défaut, tout est interconnecté, mais la programmation de la ROM permet de changer ça. Voyons ça sur un exemple d’une ROM 4x2 bits:
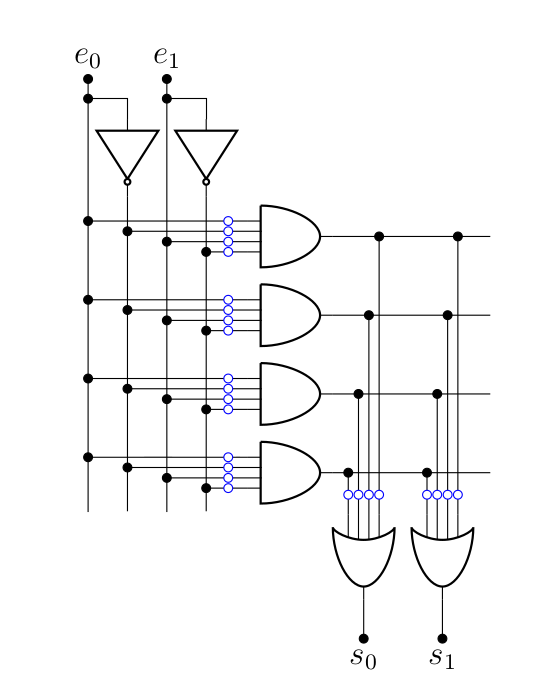
Chaque petit rond bleu est une connexion qui peut être brisée (pour ça, on peut utiliser des fusibles que l’application d’une grande tension brise). C’est le processus de "programmation" d’une ROM : passer d’un circuit comme celui présenté plus haut à un circuit correspondant à la fonction logique qu’on souhaite implémenter. En l’occurrence, pour implémenter la fonction logique et ,
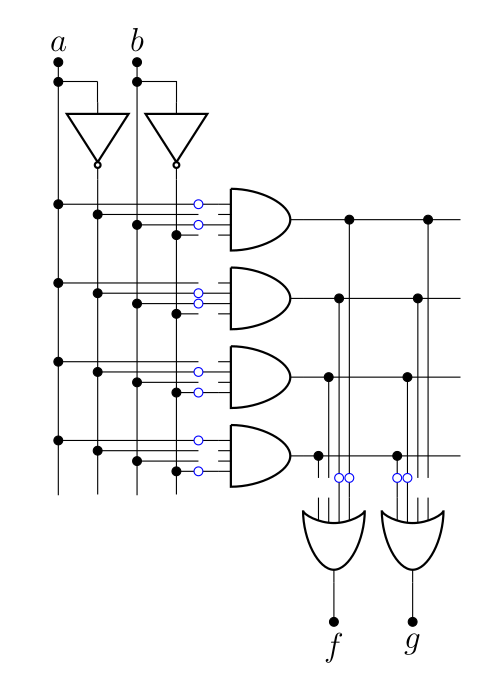
On trouve généralement un schéma simplifié pour exprimer la même chose.
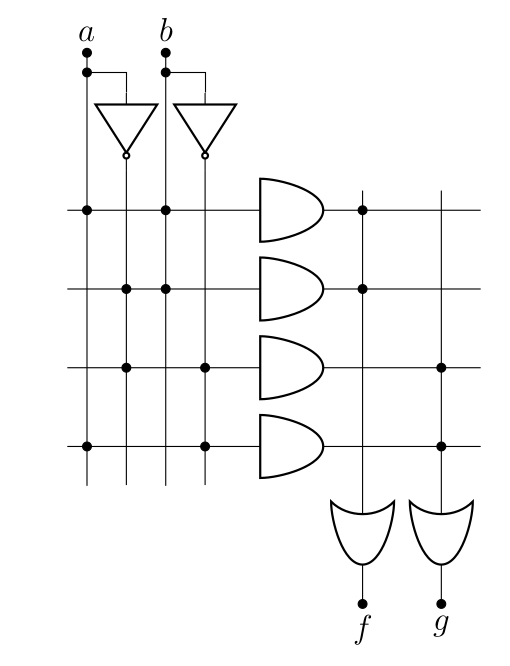
Dans le cas d’une simple PROM (avec des fusibles), la programmation ne peut être effectuée qu’une fois (au moment de sa création). Mais on a par la suite inventé les EPROM et EEPROM, qui peuvent être reprogrammées après une exposition aux rayons UV pour la première et l’aide d’un courant électrique pour la seconde (ce qui est utile lorsqu’on fait du développement de circuit).
Les ROM étaient par exemple présentes dans les anciens BIOS ou était employée dans les cartouches de jeux vidéos auparavant2 (en anglais, le mot pour les désigner est ROM cartridge, cartridge signifiant cartouche). On s’en sert toujours pour créer des tables de correspondances entre valeurs ou dans l’informatique embarquée.
Mais plus intéressant, les mémoires flashs et disque dur SSD sont en fait composés de ROM reprogrammables à l’aide de courant électriques.
Circuit avec rétroaction et logique combinatoire
Que vaut dans le circuit suivant ?
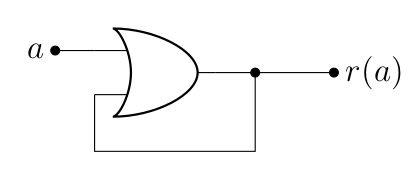
Eh bien… Ça dépend. Ça dépend en fait de ce que vaut au temps , bien entendu, ce qu’on va noter , mais ça dépend également ce que valait avant, ce qu’on va noter . En fait, on peut écrire le petit tableau suivant.
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
En fait, le plus intéressant, c’est que si , alors le circuit ne change pas de résultat (). À l’inverse, si , alors le circuit change son état pour 1 (), et rien ne pourra plus l’en faire sortir (sauf évidement de couper l’alimentation électrique). Le circuit est donc verrouillé (on parle d’un latch, en anglais).
Et ça, c’est très intéressant : d’une part parce qu’on vient de créer de la mémoire volatile (qui, ici, n’est pas réinscriptible, puisque si on inscrit 1, on ne peut plus en sortir), et d’autre par parce qu’on vient de mettre le doigt sur ce qu’on appelle de la logique séquentielle. En effet, jusqu’ici, on est resté dans le domaine de la logique combinatoire, ou la valeur d’une fonction booléenne dépend uniquement de ses entrées. Sauf que dans l’exemple ci-dessus, on a vu qu’il fallait également introduire la notion de temps, puisque la sortie de la fonction booléenne ne dépend plus seulement des valeurs d’entrée, mais également des valeurs précédentes (ou, comme on le verra plus loin, de l’instant où elles sont mesurées).
Bon, jusqu’ici, on a un circuit qui n’est pas très utile, mais on peut l’améliorer pour qu’il le soit en créant des « verroux ». L’un des exemples les plus utilisés, c’est celui qu’on peut créer avec deux portes NOR assemblées comme suit.
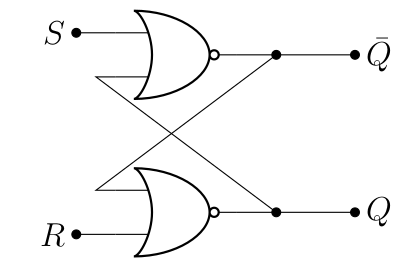
La table de vérité de ce circuit est la suivante.
| Note | |||
|---|---|---|---|
| 0 | 0 | Lecture de la valeur de | |
| 0 | 1 | 0 | Mise à 0 de |
| 1 | 0 | 1 | Mise à 1 de |
| 1 | 1 | X | Interdit |
Là, on a un élément mémoire digne de ce nom. On voit que si on met à 1 (avec ), on change la valeur de telle qu’elle soit 1 (et ce quelle que soit sa valeur précédente): et ce quel que soit la valeur précédente de (allez revoir la table de vérité de NOR si vous ne me croyez plus). Le reste suit logiquement : , donc on arrive bien à la situation où .
À l’inverse, à 1 (avec ) change la valeur de pour 0. et sont simplement les premières lettres de set et reset. La valeur de est lue en utilisant , c’est l’état verrouillé, comme dans le circuit précédent. À noter que est interdit, parce que dans ce cas, on a droit à un magnifique scénario de course (enfin, grosso modo, , ce qui n’a pas beaucoup de sens).
Ce circuit est nommé multivibrateur bistable, c’est-à-dire un circuit dont la sortie change d’état lors de la modification de l’état d’une de ces entrées, et qui garde cette position jusqu’à ce qu’on change les entrées. Le terme « multivibrateur » vient du fait que ce circuit peut également être vu comme un oscillateur électrique, produisant un signal (idéalement) carré.
Ce verrou est dit transparent, dans le sens où un changement des entrées se répercute immédiatement sur la sortie. Et ça, ça peut être un problème à cause des scénarios de courses déjà mentionnés plus haut. Idéalement, on souhaiterait que le changement ne soit possible qu’à certains moments, on va donc ajouter une entrée qui permettra d’activer le changement, qu’on va noter (pour enable). Facile, il suffit d’ajouter des portes « ET » :
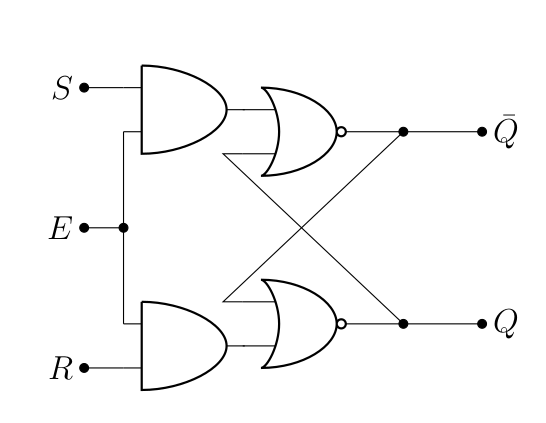
| 0 | X | X | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | X |
Sauf qu’il y a une simplification possible ! En effet, lorsqu’on change l’état du verrou (avec ), alors et sont opposés. Il suffit alors tout simplement de retirer l’une des deux entrées (on va renommer l’autre pour data), et d’utiliser une porte « NON » :
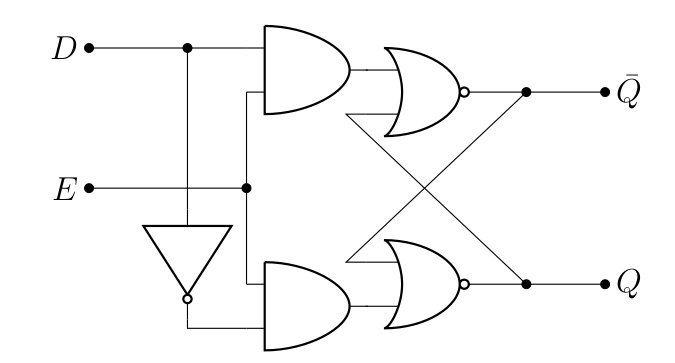
Ce qui simplifie la table de vérité :
| Note | |||
|---|---|---|---|
| 0 | X | Pas de changements | |
| 1 | 0 | 0 | Mise à 0 de |
| 1 | 1 | 1 | Mise à 1 de |
L’horloge et les flip-flops
La gestion du temps
L’horloge, c’est tout d’abord un circuit capable de passer d’un état bas (0) à un état haut (1) et inversement fois par seconde, c’est ce qu’on appelle la fréquence. La période de l’horloge est donnée par , c’est le temps qu’il faut au circuit pour partir de 0 et revenir à 0 (même chose avec 1). Avec un dessin,
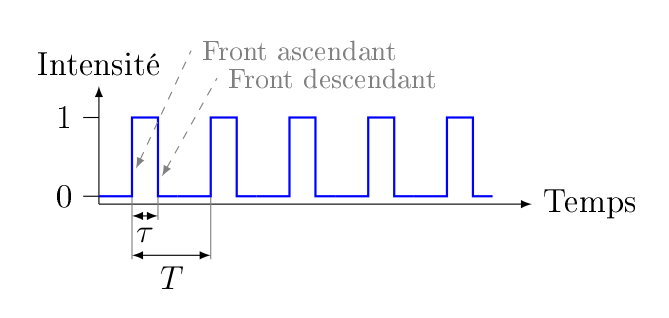
Derrière tout ça se cache un matériau piézo-électrique, c’est-à-dire un matériau qui possède la capacité de changer de forme si on lui applique un potentiel électrique (c’est un cristal de quartz qui est employé ici, et si on connaît sa forme, on peut connaître assez précisément la fréquence).
On peut également introduire le rapport cyclique : c’est la fraction de la période durant laquelle le signal est haut. Ce rapport se calcule simplement comme . Il est généralement de . L’idée, c’est que c’est ce signal qui (en plus de donner l’heure) va synchroniser les circuits électriques. Autrement dit, on va s’arranger pour que les changements n’arrivent qu’à un instant précis (tout les intervalles de temps, évidement), puis on va laisser le temps au circuit pour se stabiliser, et on est assuré qu’après un certain temps (inférieur à , ce qui fait que le choix de la période est crucial et dépend du plus lent des composants du circuit, rappelez-vous la remarque sur le calcul du report fait plus haut), la réponse qu’on mesurera(it) sera(it) la bonne.
Une fois qu’on possède un tel circuit d’horloge, on peut s’en servir pour synchroniser tous les circuits. Évidement, chacun de ceux-ci ne travaille pas à la même fréquence ( plus ou moins long), mais on peut s’arranger (la mémoire vive fonctionne par exemple plus lentement que le processeur, et c’est sans parler des mémoires plus lentes telles que les disques [durs]). Notez que la modification de la fréquence d’horloge d’un processeur est tout à fait possible, on peut ainsi l’augmenter par overclocking (sur-cadençage pour les plus français d’entre nous), mais le processeur peut également faire le travail lui-même, souvent en réduisant la fréquence pour réduire la quantité de chaleur mais aussi en l’augmentant en cas de besoin (avec des technologies comme Intel Turbo Boost (en) et AMD PowerTune (en)).
Donc la première chose à tenter, c’est de brancher le signal de notre verrou D au signal d’horloge. Quand on fait ça, on a alors un système dont les valeurs ne peuvent être modifiées que quand le signal d’horloge est haut la valeur associée au signal est de 1). On passe alors d’un verrou à une bascule (flip-flop en anglais, rien à voir avec les « chaussures » du même nom), qui se distingue d’un verrou par le fait que le circuit correspondant est synchrone.
Edge-triggered flip-flops
C’est une bonne idée, mais… puisque durant tout cet intervalle de temps , la valeur du verrou peut être modifiée, on est pas à l’abri d’un cas où la valeur de changerait plusieurs fois au cours de cet intervalle (à moins d’avoir un extrêmement faible). Du coup, on va ruser et permettre le changement uniquement quand le signal d’horloge change. Et pour ça, on peut imaginer plusieurs manières de faire. La première est de réaliser un circuit qui ne vaut 1 que quand le signal d’horloge change de valeur. Et pour ça, il suffit d’exploiter… Le scénario de course qu’on a vu plus haut, tout simplement. Imaginons que le temps pour passer au travers d’une porte « NON » soit de tandis que le passage dans une porte « ET » soit de . On peut alors mesurer la réponse du circuit suivant au cours du temps :

On voit que le signal de sortie (en rouge) ne vaut 1 que durant un bref instant qui suis le front ascendant de (on voit qu’il n’y a pas de pic correspondant au front descendant de ). On a donc une espèce de détecteur de pulsation, donc il « suffit » de minimiser et de contrôler pour obtenir quelque chose d’utilisable pour contrôler précisément quand la valeur de la bascule peut être modifiée. Notez que si on veut réaliser un circuit qui détecte le front descendant, il suffit d’utiliser une porte « NOR » à la place du « ET ». On peut donc placer un tel circuit avant l’entrée d’un verrou D pour obtenir un système tout à fait décent.
Une autre manière de faire, c’est d’assembler en série deux verrous D, contrôlés par le même signal d’horloge, dans une configuration dite « maitre-esclave »:
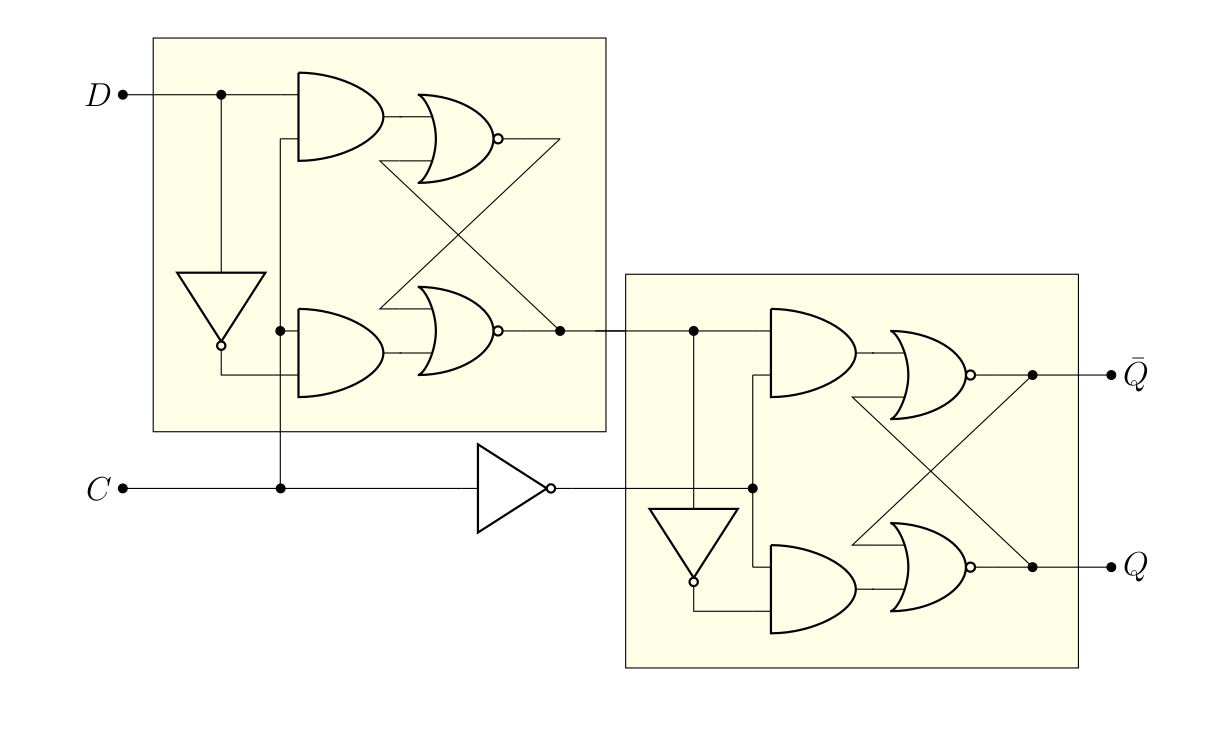
Déjà, on peut noter que le second verrou (l’esclave) ne change de valeur que si le premier (le maître) change. On peut également noter que ce changement ne peut pas être simultané, puisque les entrées permettant la modification () sont inversée sur les deux verrous. Autrement dit, on ne peut éditer la valeur du maître que si le signal d’horloge vaut 1 (mais la lecture de donnera toujours la valeur précédente), et une fois que le signal d’horloge passe à 0, l’esclave est mis à jour en conséquence (mais le maître ne peut plus être modifié). Autrement dit, ce système change de valeur sur le front descendant du signal d’horloge. Bien entendu, il y a moyen d’obtenir le même genre de circuit pour le front ascendant (en fait, il suffit de mettre une porte « NON » avant le signal d’entrée de l’horloge), mais l’idée reste la même.
Il existe bien entendu un symbole simplifié pour ces composants, que voici :
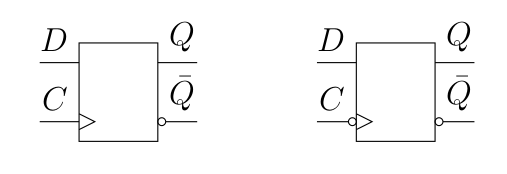
Notez qu’en pratique, c’est ce genre de bascules qui sont généralement utilisées (configuration maître-esclave). Il en existe également d’autre, telles que la bascule JK (deux verroux SR mit en série, donc un fonctionnement proche de la version D) et la bascule T, qui change de valeur de sortie (toogle, d’où le T) si son entrée (la bascule a pour équation ). Ce qui est drôle, c’est que si l’entrée est constamment maintenue à 1, alors le signal varie toutes les 2 périodes d’horloges (donc on divise la fréquence d’horloge par deux).
SRAM et DRAM
Registres et caches : SRAM
En fait, c’est comme pour l’ALU : le plus dur, c’est de faire le travail pour 1 bit, ensuite il suffit d’en mettre plusieurs d’affilée. Les registres n’y échappent pas :
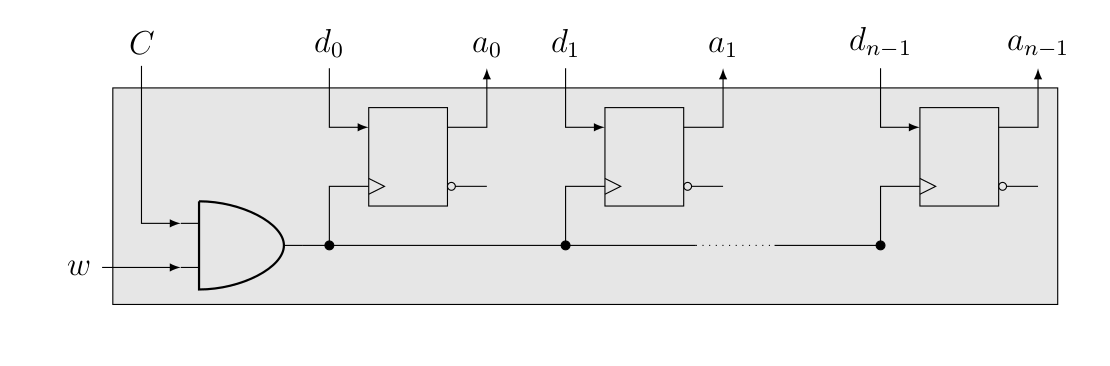
On vient de créer ce qu’on appelle de la static random-access memory, ou SRAM (même si en pratique, ce n’est plus des bascules D qui sont utilisées). Celle-ci est plus rapide que la DRAM qu’on verra juste après, bien qu’elle prenne plus de place que cette dernière (et est plus coûteuse). C’est pour ça qu’on la retrouve principalement dans les registres (pour taper sur le clou : zones de mémoires directement manipulées par le processeur), ainsi que les mémoires caches (qui ne sont pas manipulées directement par le processeur, mais contiennent des données qui sont souvent manipulées par celui-ci, ce qui accélère le calcul parce que les données sont plus rapidement accessibles que s’il fallait aller les rechercher en mémoire vive, par exemple).
Bon, et la (S)DRAM, alors ?
Rien à voir. Une des causes du coût de la SRAM, c’est le nombre de portes logiques (et donc de transistors) qu’il est nécessaire pour les créer (entre 4 et 6). Eh bien la DRAM demande deux composant pour stocker un bit : un transistor (nMOS) et un condensateur.
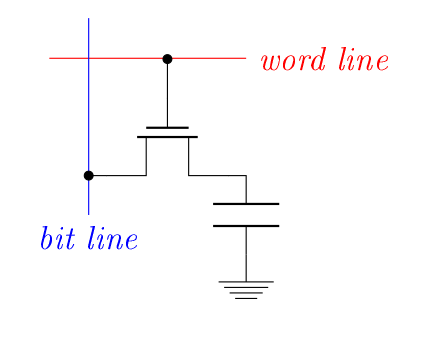
Pour rappel, un transistor nMOS ne laisse passer le courant que si un potentiel est appliqué sur sa grille (c’est comme un interrupteur). Par ailleurs, on retrouve un condensateur, dont on avait déjà expliqué le fonctionnement il y a deux chapitres, mais disons simplement qu’il permet de stocker de l’électricité, comme une micro-batterie. Bref, le concept, c’est que le condensateur stocke la présence ou l’absence de bit par présence ou absence d’électricité. À partir de là, c’est facile : la charge du condensateur n’est modifiée que quand un potentiel haut (équivalent à 1) provient de la word line (ça signifie que la cellule a été choisie). Pour écrire dans la cellule DRAM, c’est le potentiel de la bit line qui va déterminer si le condensateur va être chargé (potentiel haut) ou déchargé (potentiel bas). Pour la lecture, c’est la décharge ou nom du condensateur qui va modifier le potentiel de la bit line (qui est préalablement placé à un potentiel intermédiaire entre haut et bas) et qui va permettre de savoir si le condensateur était chargé (1) ou déchargé (0).
Quelques petites choses à préciser, tout de même :
- Ça signifie que quoiqu’il arrive, à la fin d’une opération de lecture, l’état du condensateur est inversé. Donc, il est nécessaire de faire suivre une opération de lecture par « une opération d’écriture » (recharger ou décharger le condensateur pour le replacer dans son état initial) !
- Le problème des condensateurs, c’est qu’ils ne sont pas des batteries très efficaces et qu’ils laissent du coup « échapper » le courant très rapidement. Toutes les 64 ms (ou moins), une lecture est faite afin de réécrire les données à la suite et ainsi préserver l’état de la mémoire. C’est de ce besoin périodique de rafraîchissement que provient le « D » de DRAM (dynamic), là où la SRAM n’a pas besoin d’être rafraîchie.
- On ne travaille pas par cellules individuelles, mais par « rangées » de cellules. Donc on lit par rangée, on rafraîchit l’état de toutes les cellules de la rangée en même temps et on profite d’une écriture pour également rafraîchir l’état de toute la rangée (pour être sûr). À cause de tout ça, la DRAM possède son propre circuit de gestion, indépendant du processeur et sa propre horloge (qui va normalement moins vite que celle du processeur). C’est la présence de cette horloge qui fait la SDRAM (pour synchroneous). On ne trouve aujourd’hui quasi plus que des SDRAM.
- Le terme "DDR" signifie "double data rate" et s’applique uniquement à un certain type de SDRAM. Pour réaliser ce miracle, ces mémoires transfèrent des données non seulement sur le front montant, mais aussi sur le front descendant de l’horloge (évidement, l’électronique est adaptée en fonction). Les itérations suivantes (DDR2, DDR3 et DDR4) jouent sur le nombre de données qui peuvent être transférées simultanément, l’augmentation de la fréquence d’horloge et la réduction du voltage (qui entraîne sinon des surchauffes à cause de l’effet joule).
À noter que la gestion de la mémoire par un ordinateur est un sujet crucial pour les performances, d’une part au niveau du cache (pour que les données les plus utiles soient rapidement accessibles), d’autre par parce que la demande en mémoire d’un programme excède souvent la mémoire disponible (ce qui n’est pas un problème si on le gère convenablement, avec ce qu’on appelle la mémoire virtuelle, où on va mettre l’excédent moins utile sur le disque). Mais tout ça sort du cadre de ce tutoriel.
- En vrai, on travaille plutôt au niveau de l’octet, voir du mot (64 bits sur les processeurs modernes). Mais c’est pareil. ↩
- En parlant de ça, puisque la ROM est non-modifiable, elle ne permet pas la sauvegarde, à l’inverse des mémoires volatiles qu’on verra plus loin. C’est pourquoi il y avait une pile dans les cartouches de Game Boy (et que la plupart ne fonctionnent plus aujourd’hui à moins de changer la pile).↩
Et voilà ! Il s’agissait d’un aperçu assez général et succin, et beaucoup plus pourrait être dit sur le sujet. Pour ceux que le sujet aurait intéressé, je leur conseille de faire un tour sur ce textbook (en), qui est, en plus d’être vachement complet, accessible gratuitement en ligne. Toute la section matériel et électronique se propose également à vous, dont l’incontournable tutoriel Arduino.
Sinon, après avoir été si bas dans les détails de l’électronique d’un ordinateur, il est éventuellement temps de regarder du côté du langage assembleur, qui vous permettrait d’apprendre comment un processeur (et un programmeur) réussi à exploiter tout ça. C’est également très intéressant, et il n’est pas impossible que je rajoute un jour une seconde partie à ce tutoriel pour expliquer ça.
D’ici là, bon amusement