Nous parlerons ici de collisions avec des objets plus complexes. Vous aurez besoin de connaissances mathématiques avancées pour comprendre tous les concepts. Si ce n’est pas le cas, vous pouvez néanmoins utiliser les fonctions proposées telles quelles.
Point dans polygone
Jusqu’à présent, nous avons vu les AABB et les cercles. Comment tester si un point est dans une OBB (Oriented Bounding Box), dans un triangle, un hexagone, et plus généralement dans un polygone ?
Définitions
Polygone convexe
Sans reprendre la définition exacte d’un polygone (que vous trouverez en lien à la fin de ce paragraphe), nous allons définir ce qu’est un polygone convexe. Pour cela, nous allons d’abord présenter les polygones non-convexes.
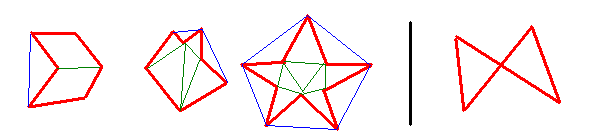
Les polygones sont en rouge. Si on regarde les 3 polygones de gauche, on peut constater qu’à chaque fois, au moins une diagonale est hors du polygone. Les diagonales sont en bleu. Je rappelle que les diagonales d’un polygone sont des segments qui relient 2 sommets quelconques du polygone, mais qui ne sont pas des côtés.
La quatrième figure est un cas tordu : un polygone croisé, c’est-à-dire qu’il y a intersection entre au moins deux de ses cotés. Nous allons vite oublier ce quatrième cas.
Un polygone convexe est un polygone non-croisé, dont toutes les diagonales sont à l’intérieur du polygone.

Les polygones ci-dessus sont donc convexes. Ils ne sont pas croisés, et il n’existe pas de diagonales à l’extérieur. Pour en savoir plus sur les polygones, et leur classification, consultez Wikipéia.
Un triangle est toujours convexe. Une OBB aussi.
De non-convexe à convexe
Un polygone non-convexe peut être transformé en un ensemble de polygones convexes. Si on regarde la figure ci-dessus sur les polygones non-convexes, j’ai ajouté des traits verts qui découpent les polygones en plusieurs triangles. Comme chaque triangle est convexe, on transforme ainsi le polygone non-convexe en plusieurs polygones convexes.
Vérifier si un point est dans ce polygone non-convexe reviendra à vérifier s’il est dans l’un des triangles qui le compose. Un algorithme pour transformer le polygone non-convexe en triangles peut être le suivant.
- On parcourt les points du polygone non-convexe.
- Pour un point i, on considère son voisin précédent et son voisin suivant. Si le triangle formé par ces trois points est dans le polygone, alors on ajoute le triangle à la liste, et on considère le polygone non-convexe restant comme étant le même polygone auquel on retire le sommet i (on relie donc i-1 et i+1).
- Etc.
C’est un algorithme glouton, et le polygone restant finit par être un triangle. On peut tester l’appartenance du triangle en regardant si l’angle du point i est aigu ou obtus par rapport au sens de parcours.
Applications
Un jeu comme Risk peut recourir à cette collision. Chaque pays peut être vu comme un polygone (non-convexe), donc par un ensemble de polygones convexes.
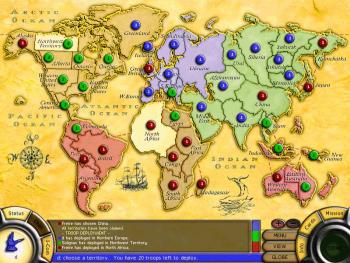
Quand vous choisissez un pays en cliquant dessus, cette collision est appliquée.
Calcul de collision première méthode
Regardez à gauche
Pour cette méthode, nous considérons un polygone convexe (s’il n’est pas convexe, regardez ci-dessus comment faire pour le décomposer en plusieurs polygones convexes).
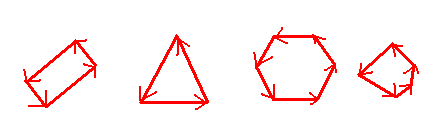
Voici de nouveau mes polygones convexes. Cette fois j’ai rajouté des flèches. En effet, je vais parcourir mes points dans l’ordre, comme si je partais d’un point, et que j’avançais en voiture sur le tour de mon polygone. L’idée est de choisir le bon sens de façon à ce que l’intérieur du polygone soit à gauche.
Un point est à l’intérieur du polygone si et seulement si il est « à votre gauche » tout le long de votre parcours.
Il va donc falloir, pour chaque coté orienté, voir si le point testé est à gauche ou non. S’il est, ne serait ce qu’une fois, à droite, alors le point n’est pas à l’intérieur.
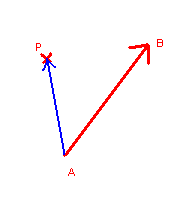
Il ne reste plus qu’a savoir si un point est à gauche ou pas. Sur la figure ci-dessus, il y a un segment [AB]. On va de A vers B. Le point P est il à gauche ?
Le déterminant
Mathématiquement, un simple calcul de déterminant suffit. Nous avons les points A, B, P. Soit D le vecteur AB :
Soit T le vecteur AP :
Soit d le déterminant de D,T. Le déterminant se calcule simplement ainsi (règle du gamma) :
- Si , alors P est à gauche de AB.
- Si , alors P est à droite de AB.
- Si , alors P sur la droite AB.
Pour le code, nous considérons le polygone comme un tableau de points, de taille . Soient les structures suivantes.
struct Point
{
float x,y;
};
struct Vecteur
{
float x,y;
};
Nous obtenons une fonction de collision comme ceci.
bool Collision(Point tab[],int nbp,Point P)
{
int i;
for(i=0;i<nbp;i++)
{
Point A = tab[i];
Point B;
if (i==nbp-1) // si c'est le dernier point, on relie au premier
B = tab[0];
else // sinon on relie au suivant.
B = tab[i+1];
Vecteur D,T;
D.x = B.x - A.x;
D.y = B.y - A.y;
T.x = P.x - A.x;
T.y = P.y - A.y;
float d = D.x*T.y - D.y*T.x;
if (d<0)
return false; // un point à droite et on arrête tout.
}
return true; // si on sort du for, c'est qu'aucun point n'est à gauche, donc c'est bon.
}
À vous de voir si vous voulez qu’un point sur AB soit considéré comme dedans ou dehors, en mettant if (d < 0) ou if (d <= 0). Cependant, ça reste un cas limite.
- Ceci fonctionne dans des repères directs. Dans les librairies 2D, on manipule souvent des repères indirects (vecteur Y vers le bas). Dans ce cas, il faudra faire attention au sens de parcours. Notez que si vous « roulez à l’envers » sur le polygone, il suffira de tester si le point est toujours à droite (et non à gauche).
- Cet algorithme marche aussi bien dans que dans .
Calcul de collision deuxième méthode
La deuxième méthode permet de tester si un point est dans un polygone quelconque. Convexe ou non, cette méthode fonctionne dans tous les cas, même dans les cas de polygones croisés. Il faudra cependant faire très attention à ce qu’on appellera les « cas limites ».
Point infini
Pour cet algo, nous allons chercher un point I qui sera en dehors du polygone. Comment être sûr qu’un point est en dehors ? Il suffit de le prendre très loin. Par exemple, on peut poser .
Nous partons du principe que notre polygone est sagement dans notre monde, et, notre monde étant par exemple compris entre -1000 et +1000, nous sommes sûr que le point est hors du monde, et hors du polygone.
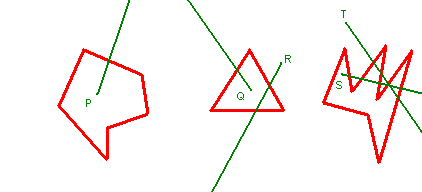
Regardons le schéma ci-dessus. Des polygones, et des segments verts dont une extrémité est un des points P, Q, R, S, T et l’autre extrémité est… loin ! Le point I est lointain.
Comptez les intersections entre le segment vert et les segments du polygone. Si le nombre d’intersections est impair, alors le point est dans le polygone, sinon il est dehors.
Vérifions tout ça avec les exemples ci-dessus.
- Pour P, on coupe une fois. Un est impair, P est à l’intérieur.
- Pour Q, idem.
- Pour R, on coupe deux fois. Deux est pair, on est à l’extérieur.
- Pour S, on coupe cinq fois, impair, on est dedans.
- Pour T, on coupe quatre fois, pair, on est dehors.
Cet algo revient donc à savoir combien de fois on coupe, donc se base sur un algo d’intersection de segments.
Intersection de segments
Un segment est inscrit dans une droite. Nous allons donc considérer l’équation paramétrique d’une droite. Ceci est vu, me semble-t-il, à la fin du lycée.
Une droite est définie par un point d’origine O, et un vecteur directeur . En faisant varier , on obtient tous les points de la droite. Si on s’intéresse à un segment [AB], posons astucieusement et .
Nous aurons donc les règles suivantes.
- Si , alors .
- Si , alors .
- Si alors appartient au segment , sinon, il n’est pas sur le segment.
Nous cherchons l’intersection de 2 segments [AB] et [IP]. Soit J le point d’intersection. Nous cherchons donc :
Où et seront les paramètres du point J sur chacune des deux droites (AB) et (IP). Ce qui nous donne :
Posons . Posons
Nous travaillons dans le plan, donc chaque point et chaque vecteur a une coordonnée x,y. Ceci nous permet de poser le système suivant.
Nous résolvons le système pour trouver et . Nous obtenons :
Si le dénominateur (qui est le même pour et ) s’annule, cela veut dire que les droites (AB) et (IJ) sont parallèles. Donc J n’existe pas (ou alors l’intersection est l’ensemble de la droite).
Sinon, cela veut dire qu’il existe un point J intersection des droites (AB) et (IJ). Mais nous, nous cherchons l’intersection des segments. Il faut donc regarder si et . Dans ce cas seulement, l’intersection se produit au niveau des segments.
Nous considèrerons qu’un point est sur le segment si (ou ) vaut 0, mais pas s’il vaut 1. En effet, au niveau des sommets du polygone, si nous ne voulons considérer qu’un seul point d’intersection, nous dirons qu’il est sur un seul des segments, celui de paramètre 0.
Nous nous appuierons sur la fonction d’intersection de segments suivante.
int intersectsegment(Point A,Point B,Point I,Point P)
{
Vecteur D,E;
D.x = B.x - A.x;
D.y = B.y - A.y;
E.x = P.x - I.x;
E.y = P.y - I.y;
double denom = D.x*E.y - D.y*E.x;
if (denom==0)
return -1; // erreur, cas limite
t = - (A.x*E.y-I.x*E.y-E.x*A.y+E.x*I.y) / denom;
if (t<0 || t>=1)
return 0;
u = - (-D.x*A.y+D.x*I.y+D.y*A.x-D.y*I.x) / denom;
if (u<0 || u>=1)
return 0;
return 1;
}
Vous pouvez constater que je retourne 0 si les segments ne se touchent pas, 1 s’ils se touchent et -1 dans les cas limites. Nous en aurons besoin pour la suite.
Fonction de collision
Nous en arrivons à la fonction de collision. Nous allons prendre un point I au hasard, mais loin. Puis nous allons calculer le nombre d’intersections avec chacun des segments. Si nous avons un nombre impair d’intersection, alors le point sera dedans, sinon dehors. Nous ajoutons que si on tombe sur un cas limite (une droite parallèle à un des cotés), nous choisirons à nouveau un autre I.
bool Collision(Point tab[],int nbp,Point P)
{
int i;
Point I;
I.x = 10000 + rand()%100; // 10000 + un nombre aléatoire entre 0 et 99
I.y = 10000 + rand()%100;
int nbintersections = 0;
for(i=0;i<nbp;i++)
{
Point A = tab[i];
Point B;
if (i==nbp-1) // si c'est le dernier point, on relie au premier
B = tab[0];
else // sinon on relie au suivant.
B = tab[i+1];
int iseg = intersectsegment(A,B,I,P);
if (iseg == -1)
return Collision(tab,nbp,P); // cas limite, on relance la fonction.
nbintersections+=iseg;
}
if (nbintersections%2==1) // nbintersections est-il impair ?
return true;
else
return false;
}
- La fonction peut être récursive en cas d’échec (cas limite). Elle pourrait donc planter si par malchance tous les
randdonnaient chacun un cas limite, ce qui lancerait une récursivité infinie. Ceci est extrêmement improbable. Il faudrait un polygone comportant beaucoup de cotés, et vraiment… vraiment tordu ! - Cet algorithme marche aussi bien dans que dans .
Segment — Cercle
Nous allons maintenant voir si un cercle touche un segment ou une droite. Nous allons faire pas mal de maths ici, si ça vous fait peur, vous pouvez prendre les fonctions finales.
Applications
Un jeu de flipper par exemple : vous testez les collisions entre la boule et chaque bord, représenté par des segments. Même les flips sont comme des segments pour les collisions.

Contre exemple : Les casse briques. Les casse briques, c’est une balle qui touche une raquette « horizontale ». Il suffit de regarder, quand le y de la balle est en deçà d’une certaine valeur, si la raquette est en dessous ou non. De même on considérera souvent la balle comme une AABB. Ici, je parlerai d’un cas général de collision entre un cercle et un segment quelconque.
Calcul de collision
Un petit schéma pour commencer.
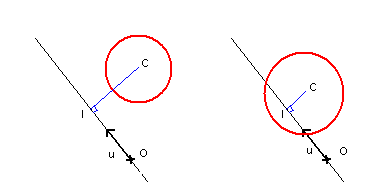
Nous avons le cercle de centre et de rayon . Nous avons la droite d’équation paramétrique . Nous souhaitons avoir la distance CI, avec le point I projection orthogonale de C sur la droite. Nous ne connaissons pas I.
Je rappelle que si on a deux points A et B, on peut définir l’équation paramétrique de la droite en posant et .
La règle est simple, et facile à voir en regardant le schéma.
Le cercle touche la droite si et seulement si la distance CI est plus petite que le rayon du cercle.
Pour un segment, il y aura une précaution supplémentaire à prendre en compte que nous verrons plus loin.
La distance CI
Un petit peu de trigo, considérons le triangle ACI rectangle en I. Le point I est inconnu, mais A et C sont connus. Nous cherchons la distance CI. Nous connaissons la distance AC, c’est la norme du vecteur .
Je rappelle que la norme d’un vecteur est sa longueur, et qu’elle se calcule ainsi :
Dans notre triangle ACI, nous pouvons écrire que , donc que avec l’angle formé entre les deux vecteurs et .
Ce qui nous embête maintenant, c’est cet angle, qu’il faudrait calculer. Soit on le calcule, soit on le vire. Une astuce est d’invoquer le produit vectoriel des deux vecteurs. Une des formules du produit vectoriel est la suivante.
or
donc :
En combinant et , nous obtenons :
Nous nous sommes débarrassé de l’angle. Nous n’avons plus qu’un produit vectoriel et deux normes à calculer. Un produit vectoriel considère des vecteurs dans l’espace. Cependant, nous sommes dans le plan, donc c’est comme si nous étions dans l’espace, mais que les coordonnées z des vecteurs étaient à 0.
A partir de là, la norme d’un produit vectoriel sera un vecteur dont les composantes x et y seront nulles, et seule sa composante z sera non nulle. Prendre la norme de ce vecteur reviendra à prendre la valeur absolue de cette composante z, comme ceci :
et donc, dans notre cas :
Il suffira de diviser cette valeur absolue par la norme de u pour obtenir CI. Et il nous suffira donc de savoir si CI est plus grand que le rayon ou non. Voici le code pour tester si le cercle C touche la droite AB.
bool CollisionDroite(Point A,Point B,Cercle C)
{
Vecteur u;
u.x = B.x - A.x;
u.y = B.y - A.y;
Vecteur AC;
AC.x = C.x - A.x;
AC.y = C.y - A.y;
float numerateur = u.x*AC.y - u.y*AC.x; // norme du vecteur v
if (numerateur <0)
numerateur = -numerateur ; // valeur absolue ; si c'est négatif, on prend l'opposé.
float denominateur = sqrt(u.x*u.x + u.y*u.y); // norme de u
float CI = numerateur / denominateur;
if (CI<C.rayon)
return true;
else
return false;
}
Restriction au segment
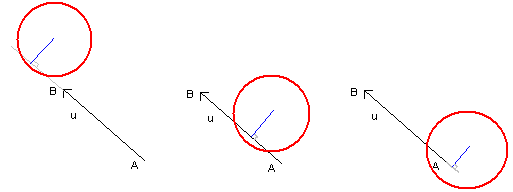
Tout d’abord, si le cercle ne touche pas la droite (AB), il ne touchera jamais le segment [AB]. Ensuite, si le cercle touche la droite, il touchera le segment si le point d’intersection I est entre A et B (cas 2 ci dessus), mais aussi si A ou B sont dans le cercle (cas 3 contre cas 1 ci-dessus).
Pour le test d’un point dans un cercle, je vous renvoie au début de ce tutoriel. Alors l’idée est de savoir si I est entre A et B.
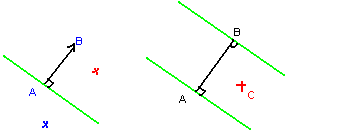
Pour cela, nous allons utiliser le produit scalaire, rapide, et qui a des propriétés bien sympathiques. Regardez le dessin de gauche.
J’ai les points A,B qui me donnent un vecteur , qui part de A. Au point A, on imagine une frontière verte, orthogonale au vecteur. Si on appelle P l’un des points (rouge ou bleu), le signe du produit scalaire nous permet de savoir de quel coté de la ligne verte on est. Si le produit scalaire est positif, on est du coté de B, sinon, on est de l’autre coté.
Cette astuce est fort utile dans les jeux vidéos. Imaginons que vous soyez un héro au point A, que vous regardez en direction du point B. Un monstre arrive (c’est un point P). Comme savoir si le monstre est devant vous ou derrière vous ? … Et ainsi selon que le signe de ce produit scalaire est positif ou non, vous voyez le monstre ou non.
Maintenant, nous voulons savoir si I est entre A et B. Regardons le dessin de droite ci-dessus. Comme I est le projeté orthogonal de C sur la droite, alors pour savoir si I est entre A et B, il suffit de regarder si C est dans la bande verte ou non. Pour cela, on applique 2 produits scalaires :
Si ET , alors C est dans la bande verte, et donc I entre A et B. Cela nous donne la fonction suivante.
bool CollisionSegment(Point A,Point B,Cercle C)
{
if (CollisionDroite(A,B,C) == false)
return false; // si on ne touche pas la droite, on ne touchera jamais le segment
Vecteur AB,AC,BC;
AB.x = B.x - A.x;
AB.y = B.y - A.y;
AC.x = C.x - A.x;
AC.y = C.y - A.y;
BC.x = C.x - B.x;
BC.y = C.y - B.y;
float pscal1 = AB.x*AC.x + AB.y*AC.y; // produit scalaire
float pscal2 = (-AB.x)*BC.x + (-AB.y)*BC.y; // produit scalaire
if (pscal1>=0 && pscal2>=0)
return true; // I entre A et B, ok.
// dernière possibilité, A ou B dans le cercle
if (CollisionPointCercle(A,C))
return true;
if (CollisionPointCercle(B,C))
return true;
return false;
}
Le point d’impact
Actuellement, nous avons une information sur l’entrée en collision ou non. Mais il peut être utile de savoir à quel endroit on touche. On touche au point I bien entendu, mais comment calculer I ?
Nous avons vu que notre droite a pour équation (avec dans notre cas). I appartient à la droite, donc il existe t_i tel que .
Si on regarde le triangle AIC rectangle en I, de nouveau, avec un peu de trigonométrie, on trouve , avec angle au sommet A.
Ici, il est astucieux de considérer la formule suivante du produit scalaire.
Sachant que , en utilisant (6) et (7), on trouve :
Si on veut , il faut diviser par la norme de . Cela donne :
Cela nous épargnera, au niveau optimisation, de calculer la racine carrée de la norme de puisqu’on la considère au carré.
Nous obtenons la formule finale suivante :
Au niveau du code nous avons donc une droite (AB), et un point C à projeter.
Point ProjectionI(Point A,Point B,Point C)
{
Vecteur u,AC;
u.x = B.x - A.x;
u.y = B.y - A.y;
AC.x = C.x - A.x;
AC.y = C.y - A.y;
float ti = (u.x*AC.x + u.y*AC.y)/(u.x*u.x + u.y*u.y);
Point I;
I.x = A.x + ti*u.x;
I.y = A.y + ti*u.y;
return I;
}
La normale
La normale est le vecteur orthogonal à la tangente qui « regarde » le point C. Avoir la normale au point d’impact permet de calculer un rebond par exemple. Sur une droite, la normale est constante en tout point.
On utilise souvent le produit vectoriel pour calculer des normales. Ici, on fera pareil, en utilisant deux produits vectoriels, un pour calculer un vecteur orthogonal à notre plan , puis on refera un autre produit vectoriel pour trouver notre normale .
L’avantage de cette méthode, c’est que la normale « regardera » toujours C, qu’il soit d’un coté ou de l’autre de la droite. Cet algo fonctionne aussi dans l’espace, pour trouver le vecteur .
Si on appliques les formules des deux produits vectoriels, on trouve simplement, pour la normale :
Il est d’usage qu’une normale soit normalisée… autrement dit que sa norme (sa longueur) soit 1. Il suffit de diviser N par sa norme :
Au niveau du code, cela nous donne la chose suivante.
Vecteur GetNormale(Point A,Point B,Point C)
{
Vecteur AC,u,N;
u.x = B.x - A.x;
u.y = B.y - A.y;
AC.x = C.x - A.x;
AC.y = C.y - A.y;
float parenthesis = u.x*AC.y-u.y*AC.x; // calcul une fois pour les deux
N.x = -u.y*(parenthesis);
N.y = u.x*(parenthesis);
// normalisons
float norme = sqrt(N.x*N.x + N.y*N.y);
N.x/=norme;
N.y/=norme;
return N;
}
Une utilisation de tout ça : le rebond
Voici une utilisation pratique de tout ça : un calcul de rebond. Un jeu de flipper par exemple : votre balle arrive sur un mur en biais, vous voulez calculer le rebond. Dans quel sens va-t-elle repartir ?
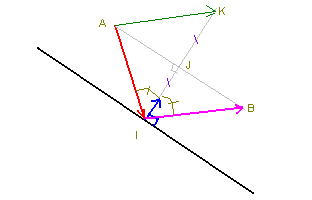
Regardons le dessin ci-dessus. La balle (qu’on ne voit pas) arrive avec une trajectoire suivant le vecteur rouge (de A vers I). Après rebond, il faudra qu’elle reparte avec la trajectoire violet, de I vers B.
Nous calculons grâce à la fonction de collision si on touche la droite. Ensuite, si on touche, il faut faire rebondir. Pour cela, on aura besoin de la normale (en bleu) au segment (qu’on calculera comme vu au dessus).
Le vecteur est tel que la normale soit la bissectrice des vecteurs et au point I. Sur le dessin, j’ai mis les angles égaux.
J est le projeté orthogonal de A sur la droite faite par le point I et la normale. Le vecteur est le même que le vecteur , en partant de A au lieu de I, mais c’est le même vecteur. Géométriquement, on peut démontrer que J est le milieu de [IK], et J est aussi le milieu de [AB].
Le vecteur est normalisé : rappelez vous, les normales sont normalisées.
La longueur IJ (qu’on pourra aussi appeler ) s’obtient à partir d’un produit scalaire :
Je considère IA et non AI pour avoir une longueur positive. On veut calculer le vecteur , donc . Géométriquement :
On simplifie :
En injectant (7), je trouve :
Enfin, un petit code pour terminer cette grande partie. On donne le vecteur () incident, et la normale, et on calculera le vecteur de rebond.
Vecteur CalculerVecteurV2(Vecteur v,Vecteur N)
{
Vecteur v2;
float pscal = (v.x*N.x + v.y*N.y);
v2.x = v.x -2*pscal*N.x;
v2.y = v.y -2*pscal*N.y;
return v2;
}
Segment — Segment
Voici maintenant une collision Segment — Segment.
Pourquoi cette collision ?
Nous pouvons penser que ce genre n’est pas trop utilisée, car un personnage est rarement représenté par un segment. Il peut être représenté par un point, par une AABB, un polygone, un cercle… Mais rarement un segment. Cependant, en raisonnant comme cela, vous pensez à un état figé.
Maintenant, regardez ce schéma.
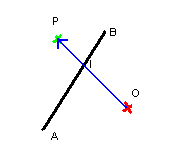
Votre personnage est le point O. Il y a un mur, représenté par le segment AB. Il veut avancer vers le point P (donc selon le vecteur OP). Se prend-il le mur ? Pour le savoir, nous regarderons la collision entre les segments [AB] et [OP].
Applications
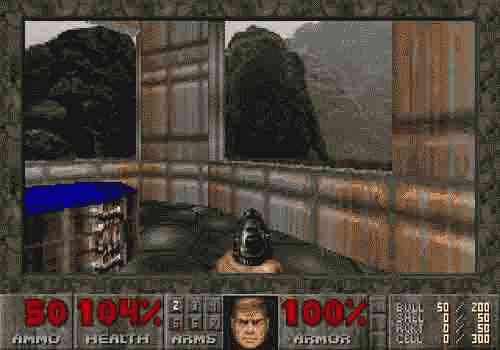
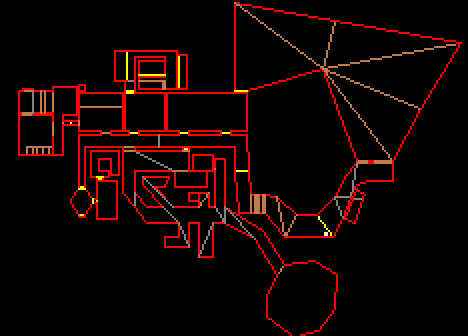
Quoi ? Un jeu 3D comme Doom dans la rubrique 2D ? 
Oh que oui… Le premier Doom, une merveille, un jeu faussement 3D. Un amas de trapèzes qui nous font penser à la 3D, mais un jeu en interne bien 2D…
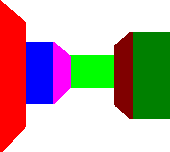
Quel beau monde en 3D n’est ce pas ? Un beau couloir multicolore… Dites merci à votre cerveau de vous faire voir un monde en 3D, parce que moi je n’ai dessiné que des trapèzes (un rectangle est un trapèze particulier). Des trapèzes dont les bases sont alignées avec l’axe des Y, bien droit. Voila, dans Doom, tous les murs sont des trapèzes.
Mais ça, c’est l’affichage. En réalité, dans Doom, en mémoire, il n’y a qu’une map 2D, comme la 2ème image que je présente ici, ces segments rouges et jaunes (mais pas à petits pois, la génération Dorothée comprendra la blague).
Donc dans Doom, le personnage est un point dans une carte 2D faite de plein plein de segments qui représentent les murs. Nous sommes donc tout à fait dans le cas vu plus haut, à savoir que nous sommes un point O, nous voulons avancer vers P. Touchons nous le segment [AB] ?
Calcul de collision
Nous allons calculer cette collision en deux étapes.
Tout d’abord, il peut y avoir collision seulement si O et P ne sont pas du même coté de la droite (AB).
En effet, si P et O sont du même coté de la droite (AB), on peut tout de suite dire « il n’y aura pas collision ». On peut donc calculer la collision entre le segment [OP] et la droite (AB).
Calcul de collision entre segment et droite
Rappelez vous le calcul du déterminant de deux vecteurs qui me dit si un point est « à gauche » ou « à droite » d’une droite. Si on considère le vecteur AB, et le vecteur AP, le déterminant de me dit si mon point P est à gauche ou à droite du mur (en considérant le mur comme « démarrant » au point A et « regardant » le point B).
- Si , P est à gauche.
- Si , P est à droite.
- Si , P est dans le mur : on va éviter ce cas là.
On va partir du principe que P n’est jamais dans le mur. En effet, dans un jeu comme Doom, on commence hors d’un mur, et quand on évolue, on ne permet pas d’aller « dans » le mur. On permet d’aller proche, mais jamais dedans. Donc on n’est jamais « dans » un mur. Donc n’est jamais égal à 0.
Maintenant, on calcule le déterminant et pour savoir de quel coté sont P et O.
- Si et , alors ils sont du même coté.
- Si et , alors ils sont du même coté.
- Si et , alors ils ne sont pas du même coté.
- Si et , alors ils ne sont pas du même coté.
Ça nous fait quatre conditions à voir, sauf si on pense aux propriétés de la multiplication, qui vont nous simplifier le travail.
- Si , alors ils sont du même coté.
- Si , alors ils ne sont pas du même coté.
Au niveau du code, cela donne ceci.
bool CollisionDroiteSeg(Point A,Point B,Point O,Point P)
{
Vecteur AO,AP,AB;
AB.x = B.x - A.x;
AB.y = B.y - A.y;
AP.x = P.x - A.x;
AP.y = P.y - A.y;
AO.x = O.x - A.x;
AO.y = O.y - A.y;
if ((AB.x*AP.y - AB.y*AP.x)*(AB.x*AO.y - AB.y*AO.x)<0)
return true;
else
return false;
}
Calcul de collision entre segment et segment
Une idée simple pour calculer la collision entre segment et segment est de se servir deux fois de la formule ci dessus. Si vous avez quatre points ABOP, que vous voulez calculer la collision entre le segment [AB] et le segment [OP], il suffit de calculer la collision entre la droite (AB) et le segment [OP], puis la collision entre la droite (OP) et le segment [AB]. Si les deux collisions sont valides, alors les segments se touchent.
Au niveau du code, cela donne :
bool CollisionSegSeg(Point A,Point B,Point O,Point P)
{
if (CollisionDroiteSeg(A,B,O,P)==false)
return false; // inutile d'aller plus loin si le segment [OP] ne touche pas la droite (AB)
if (CollisionDroiteSeg(O,P,A,B)==false)
return false;
return true;
}
Calcul de collision entre segment et segment, forme paramétrique
Cette méthode est plus complexe que la précédente, mais permettra de calculer le point d’intersection. Grâce au calcul segment/droite, on sait que les points O et P sont de part et d’autre de la droite (AB), mais il y a collision segment/segment seulement si le point d’intersection I est entre A et B. Sinon, le personnage passe à coté du mur : il n’y a pas collision.
Nous allons donc voir si l’intersection est entre A et B ou non. De cette condition dépendra notre collision. Posons la forme paramétrique de la droite (AB) :
Avec cette forme, nous pouvons affirmer que I est entre A et B si et seulement si . Il ne reste plus qu’à trouver . I appartient également à la droite (OP), donc :
Du coup, on peut écrire :
Nous sommes dans le plan, nous pouvons décomposer les points et les vecteurs comme suit :
Nous avons donc deux équations et deux inconnues ( et ). Si nous résolvons ce système, nous obtenons :
Notez que pour notre cas, nous n’avons pas besoin de . Je le mets quand même car on en aura besoin plus loin si on veut s’approcher au plus près du mur.
Voici la fonction de collision Segment-Segment.
bool CollisionSegSeg(Point A,Point B,Point O,Point P)
{
if (CollisionDroiteSeg(A,B,O,P)==false)
return false; // inutile d'aller plus loin si le segment [OP] ne touche pas la droite (AB)
Vecteur AB,OP;
AB.x = B.x - A.x;
AB.y = B.y - A.y;
OP.x = P.x - O.x;
OP.y = P.y - O.y;
float k = -(A.x*OP.y-O.x*OP.y-OP.x*A.y+OP.x*O.y)/(AB.x*OP.y-AB.y*OP.x);
if (k<0 || k>1)
return false;
else
return true;
}
Ne pas aller dans le mur
Pour terminer ce chapitre, quelques idées pour éviter de se retrouver dans le mur. Si vous êtes le point O et que vous allez vers le mur, alors il y aura collision. L’idée est d’avancer quand même « jusqu’au mur ».
Comme nous allons dans le mur, nous ne déplacerons pas notre joueur selon le vecteur , qui nous amènerait au-delà du mur (au point P). Nous ne le déplacerons pas non plus selon le vecteur , qui nous amènerait dans le mur exactement (ce que nous voulons absolument éviter, il ne faut jamais être « dans » le mur).
Nous déplacerons le joueur selon le vecteur où est un nombre positif très petit (un « epsilon » dit-on dans le jargon mathématique), par exemple 0.001. Ainsi, nous nous approcherons au plus près du mur, sans être dedans, ni passer à travers.
Bien que ce genre d’algorithme pourrait marcher avec des nombres entiers, (dans ) en faisant attention aux arrondis, il est préférable d’utiliser des coordonnées réelles (dans ) pour cet algorithme.
Cercles — AABB
Nous cherchons maintenant à déterminer la collision entre un cercle et une AABB.
Cette collision pourra, dans certains cas tordus, être un peu calculatoire. C’est pour cela que l’idée sera d’éliminer le plus rapidement possible les cas triviaux. Comme ces cas seront majoritaires, la collision sera en moyenne très rapide.
Regardons le schéma suivant.
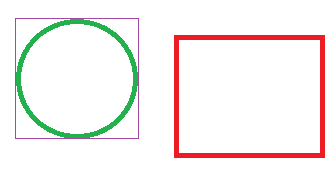
Je souhaite tester la collision entre le cercle vert, et la AABB rouge.
Première étape, le cercle peut être lui même inscrit dans une AABB, que l’on peut calculer facilement. Mieux, si votre sprite est une balle, sa surface porteuse sera rectangulaire, et sera directement la AABB violette : vous n’aurez donc même pas à la calculer, il suffira de passer la surface porteuse !
Premier test
Premier test, nous allons tester la collision AABB vs AABB de nos deux AABB rouge et violette. Ce test est rapide, et élimine déjà tous les cas ou les objets sont suffisamment loin. En effet, s’il n’y a pas collision entre ces deux AABB, inutile d’aller plus loin : il n’y a pas collision.
Vous éliminez ici d’entrée la grande majorité des cas ! 
S’il y a collision AABB, alors nous sommes dans l’un de ces cas.
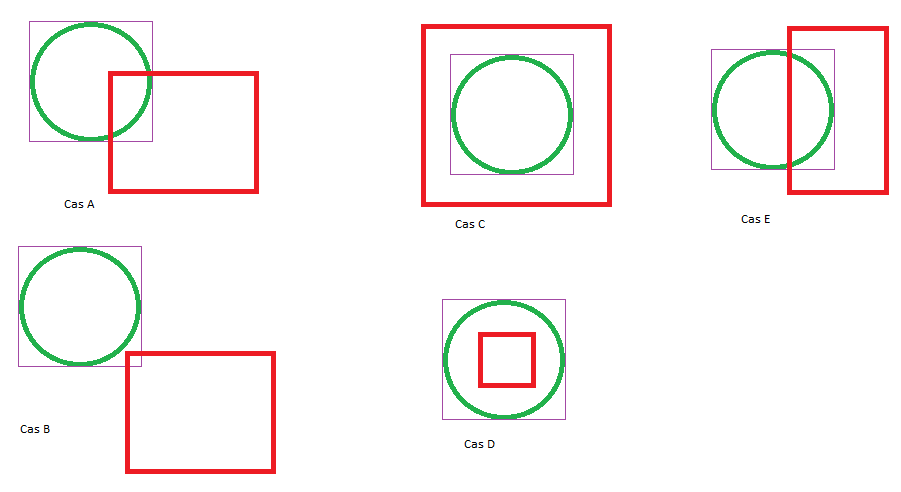
Nous allons continuer à éliminer rapidement les cas triviaux.
Deuxième test
Nous allons voir si un des sommets de la AABB rouge est dans le cercle, grâce à la collision rapide « Point dans Cercle » vue plus haut. Nous pourrons alors dire qu’il y a collision dans les cas A et D, et sortir de l’algorithme.
Troisième test
Afin de détecter le cas C, nous allons faire une collision « Point dans AABB » sur le centre du cercle et la AABB rouge. Nous pouvons alors sortir de l’algorithme dans ce cas.
A partir d’ici, cela devient plus calculatoire : nous sommes soit dans le cas B, soit dans le cas E. La bonne nouvelle, c’est que dans la majorité des cas, nous serons sortis avant.
Quatrième test
Il faut donc lever l’ambiguïté entre le cas B, et le cas E. La différence entre ces deux cas, se situe au niveau des segments de la AABB.
Nous allons considérer chacun des 4 segments de la AABB. Pour chacun de ces segments, nous allons projeter le point centre du cercle sur le segment. Si la projection est sur le segment, alors nous sommes dans le cas E, si elle est hors du segment, alors on est dans le cas B.
Si on regarde le schéma suivant :
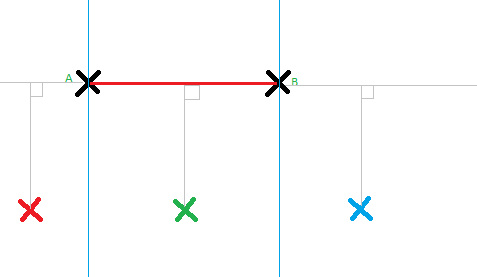
Nous avons le segment AB. Nous projetons un point dessus, soit le rouge, soit le vert, soit le bleu. Seul le vert est projeté sur le segment, les deux autres sont hors du segment. Cela signifie que le point vert est entre les deux droites bleu ciel, droites passant respectivement par A et B et perpendiculaires au segment AB.
Pour déterminer si le point sera projeté sur le segment ou dehors, c’est assez simple. Soit C le point à tester. Nous allons considérer les produits scalaires suivants :
Le signe de ces produits scalaires va nous donner immédiatement la réponse.
- Si et , alors nous sommes hors du segment, coté B (point bleu).
- Si et , alors nous sommes hors du segment, coté A (point rouge).
- Si et , alors nous sommes dans le segment (point vert).
- Si et , alors nous avons un grave problème mathématique… Ce cas n’existe pas !
Évidemment, nous avons aussi les cas limites où s1 == 0, s2 == 0. Mais pour simplifier, basons-nous sur la règle des signes.
- Si
s1 * s2 > 0, on est dehors. - Sinon, on est dedans.
Vous pouvez remplacer > 0 par >= 0 si vous considérez le segment comme ouvert : au lieu de .
Après avoir fait ces projections sur les quatre segments de la AABB (en réalité, deux suffisent car les segments sont parallèles et « en face » deux à deux) ; si les points calculés sont tous dehors, nous sommes dans le cas B (pas de collision), sinon nous sommes dans le cas E (collision).
Et pour finir, petit algorithme formel pour illustrer.
bool CollisionCercleAABB(Cercle C1,AABB box1)
{
AABB boxCercle = GetBoxAutourCercle(C1); // retourner la bounding box de l'image porteuse, ou calculer la bounding box.
if (CollisionAABBvsAABB(box1,boxCercle)==0)
return false; // premier test
if (CollisionPointCercle(box1.x,box1.y,C1)==1
|| CollisionPointCercle(box1.x,box1.y+box1.h,C1)==1
|| CollisionPointCercle(box1.x+box1.w,box1.y,C1)==1
|| CollisionPointCercle(box1.x+box1.w,box1.y+box1.h,C1)==1)
return true; // deuxieme test
if (CollisionPointAABB(C1.x,C1.y,box1)==1)
return true; // troisieme test
int projvertical = ProjectionSurSegment(C1.x,C1.y,box1.x,box1.y,box1.x,box1.y+box1.h);
int projhorizontal = ProjectionSurSegment(C1.x,C1.y,box1.x,box1.y,box1.x+box1.w,box1.y);
if (projvertical==1 || projhorizontal==1)
return true; // cas E
return false; // cas B
}
int ProjectionSurSegment(int Cx,int Cy,int Ax,int Ay,int Bx,int By)
{
int ACx = Cx-Ax;
int ACy = Cy-Ay;
int ABx = Bx-Ax;
int ABy = By-Ay;
int BCx = Cx-Bx;
int BCy = Cy-By;
int s1 = (ACx*ABx) + (ACy*ABy);
int s2 = (BCx*ABx) + (BCy*ABy);
if (s1*s2>0)
return 0;
return 1;
}
Nous verrons avec le temps les collisions d’autres objets complexes.