Dans cette partie nous allons implémenter la FFT en partant d’une approche simple, puis en complexifiant au fur et à mesure pour essayer de calculer la transformée de Fourier d’un signal réel de la manière la plus efficace possible. Pour comparer les performances de nos implémentations, nous continuerons à comparer avec l’implémentation de FFTW.
- Ma première FFT
- Analyse de la première implémentation
- Calculer la permutation inverse des bits
- Ma seconde FFT
- Le cas particulier d'un signal réel
- Une FFT pour les réels
- Optimisation des fonctions trigonométriques
Ma première FFT
Nous avons trouvé précédemment l’expression de la transformée de Fourier discrète :
L’astuce au cœur de l’algorithme de la FFT consiste à remarquer que si l’on essaie de couper cette somme en deux, en séparant les termes pairs et les termes impairs, on obtient (en supposant que soit pair), pour :
où et sont les transformées de Fourier de la séquence des termes pairs de et de la séquence des termes impairs de . On peut donc calculer la première moitiée de la transformée de Fourier de en calculant les transformées de Fourier de ces deux séquences de longueur et en les recombinant. De même, si on calcule on a :
Cela signifie qu’en calculant deux transformées de Fourier de longueur , on est capable de calculer deux éléments d’une transformée de Fourier de longueur . En supposant pour simplifier que soit une puissance de deux1, cela dessine naturellement une implémentation récursive de la FFT. D’après le master theorem, cet algorithme sera de complexité , ce qui est bien mieux que le premier algorithme naïf que nous avons implémenté, qui présente une complexité en .
function my_fft(x)
# Condition d'arrêt, la TF d'un tableau de taille 1 est ce même tableau.
if length(x) <= 1
x
else
N = length(x)
# Xᵒ contient la TF des termes impairs et Xᵉ celle des termes pairs.
# La subtilité étant que les tablaux de Julia commencent à 1 et non à 0.
Xᵒ = my_fft(x[2:2:end])
Xᵉ = my_fft(x[1:2:end])
factors = @. exp(-2im * π * (0:(N/2 - 1)) / N)
[Xᵉ .+ factors .* Xᵒ; Xᵉ .- factors .* Xᵒ]
end
end
On peut vérifier comme précédemment que code donne un résultat juste, puis comparer ses qualités d’exécution avec l’implémentation de référence.
let
@benchmark fft(a) setup=(a = rand(1024))
end
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 26.516 μs … 14.073 ms ┊ GC (min … max): 0.00% … 53.68%
Time (median): 31.983 μs ┊ GC (median): 0.00%
Time (mean ± σ): 35.044 μs ± 140.536 μs ┊ GC (mean ± σ): 2.16% ± 0.54%
█▅ ▃▄▃▆▇▃
▁▃▅▄██████████▇▇▆▄▃▃▂▂▂▁▁▂▂▂▁▁▁▁▂▁▁▂▁▂▂▂▂▂▂▂▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁ ▃
26.5 μs Histogram: frequency by time 55.5 μs <
Memory estimate: 34.19 KiB, allocs estimate: 34.
let
@benchmark my_fft(a) setup=(a = rand(1024))
end
BenchmarkTools.Trial: 1174 samples with 1 evaluation.
Range (min … max): 3.538 ms … 29.072 ms ┊ GC (min … max): 0.00% … 82.07%
Time (median): 3.964 ms ┊ GC (median): 0.00%
Time (mean ± σ): 4.248 ms ± 2.232 ms ┊ GC (mean ± σ): 4.89% ± 7.97%
█▁ ▃▁▁▁
█▄▆████████▇▇▅▅▅▄▅▃▃▃▃▃▂▃▃▃▂▂▂▂▂▂▂▁▂▁▁▂▂▂▁▂▁▁▁▁▁▁▁▁▂▁▂▂▁▁▂ ▃
3.54 ms Histogram: frequency by time 6.65 ms <
Memory estimate: 1.09 MiB, allocs estimate: 14322.
On voit que l’on a bien amélioré le temps d’exécution (d’un facteur 8) et l’empreinte mémoire de l’algorithme (d’un facteur 13), sans pour autant se rapprocher de l’implémentation de référence.
- En pratique on peut toujours se ramener à ce cas en faisant du bourrage de zéros.↩
Analyse de la première implémentation
Reprenons le code précédent :
function my_fft(x)
# Condition d'arrêt, la TF d'un tableau de taille 1 est ce même tableau.
if length(x) <= 1
x
else
N = length(x)
# Xᵒ contient la TF des termes impairs et Xᵉ celle des termes pairs.
# La subtilité étant que les tablaux de Julia commencent à 1 et non à 0.
Xᵒ = my_fft(x[2:2:end])
Xᵉ = my_fft(x[1:2:end])
factors = @. exp(-2im * π * (0:(N/2 - 1)) / N)
[Xᵉ .+ factors .* Xᵒ; Xᵉ .- factors .* Xᵒ]
end
end
Et essayons de suivre les allocations de mémoire. Pour simplifier, on peut supposer que l’on travaille sur un tableau de 4 éléments, [f[0], f[1], f[2], f[3]]. Le premier appel à my_fft garde en mémoire le tableau initial, puis lance la fft sur deux sous tableaux de taille 2 : [f[0], f[2]] et [f[1], f[3]], puis les appels récursifs gardent en mémoire avant de recombiner les tableaux [f[0]] et [f[2]] puis [f[1]] et [f[3]]. Au plus, on a donc tableaux alloués avec des tailles divisées par deux à chaque fois. Non seulement ces tableaux occupent de la mémoire, mais en plus on perd du temps à les allouer !
Or si l’on observe la définition de la récurrence que l’on utilise, à chaque étape (c’est-à-dire pour chaque taille de tableaux, ), la somme des tailles des tableaux intermédiaires est toujours . Autrement dit, cela donne l’idée que l’on pourrait s’épargner toutes ces allocations de tableaux et utiliser en permanence le même tableau, à condition de réaliser toutes les associations de tableaux de même taille à la même étape.
Schématiquement on peut représenter le processus de la FFT pour un tableau à 8 éléments ainsi :
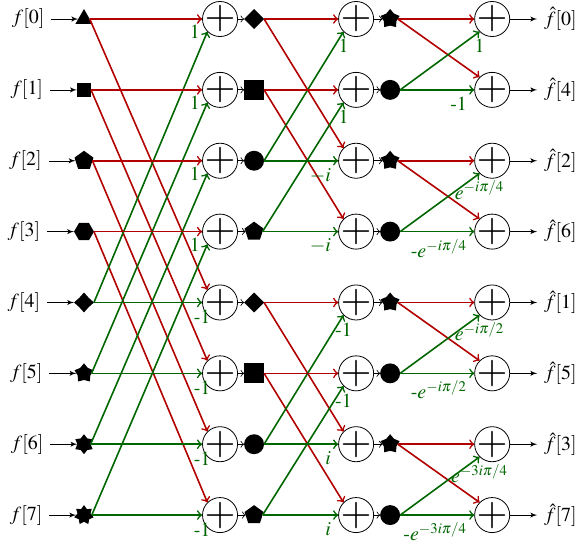
Comment lire ce schéma ? Chaque colonne correspond à une profondeur de la récurrence de notre première FFT. La colonne la plus à gauche correspond à la récurrence la plus profonde : on a découpé le tableau d’entrée suffisamment pour arriver à des sous-tableaux de taille 1. Ces 8 sous-tableaux sont symbolisés par 8 formes géométriques différentes. On passe ensuite au niveau de récurrence supérieur. Chaque paire de sous-tableaux de taille 1 doit être combinée pour créer un sous-tableau de taille 2, qui sera stocké dans les mêmes cases mémoire que les deux sous-tableaux de taille 1. Par exemple, on combine le sous-tableau ▲ qui contient et le sous-tableau ◆ qui contient en utilisant la formule démontrée précédemment pour former le tableau , que j’ai appelé dans la suite ◆, et on stocke les deux valeurs en position 0 et 4. Les couleurs des flèches permettent de distinguer celles portant un coefficient (qui correspondent au traitement que l’on fait subir au sous-tableau dans les formules de la section précédente). Après avoir construit les 4 sous-tableaux de taille 2, on peut passer à une nouvelle étape de la récurrence pour calculer deux sous-tableaux de taille 4. Enfin la dernière étape de la récurrence combine les deux sous-tableaux de taille 4 pour calculer le tableau de taille 8 qui contient la transformée de Fourier.
En s’inspirant de ce schéma on peut penser à avoir une fonction dont la boucle principale calculerait successivement chaque colonne pour arriver au résultat final. De cette manière on effectue tous les calculs sur un seul et même tableau et on minimise le nombre d’allocations ! Il y a cependant un problème: on voit que les ne semblent pas ordonnés à la fin du processus.
En réalité, ces sont ordonnés via une permutation inverse des bits. Cela signifie que si l’on écrit les indices en binaire, puis que l’on inverse cette écriture (le MSB devenant le LSB1), on obtient l’indice auquel se trouve après l’algorithme de FFT. Le process de permutation est décrit par le tableau suivant dans le cas d’un calcul sur 8 éléments.
| Représentation binaire de | Représentation binaire inversée | Indice de | |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Si on sait calculer la permutation inverse des bits, on peut simplement réordonner à la fin du processus le tableau pour obtenir le bon résultat. Cependant avant de se jeter sur l’implémentation il est intéressant de regarder ce qu’il se passe si à la place on réordonne le tableau d’entrée via cette permutation.
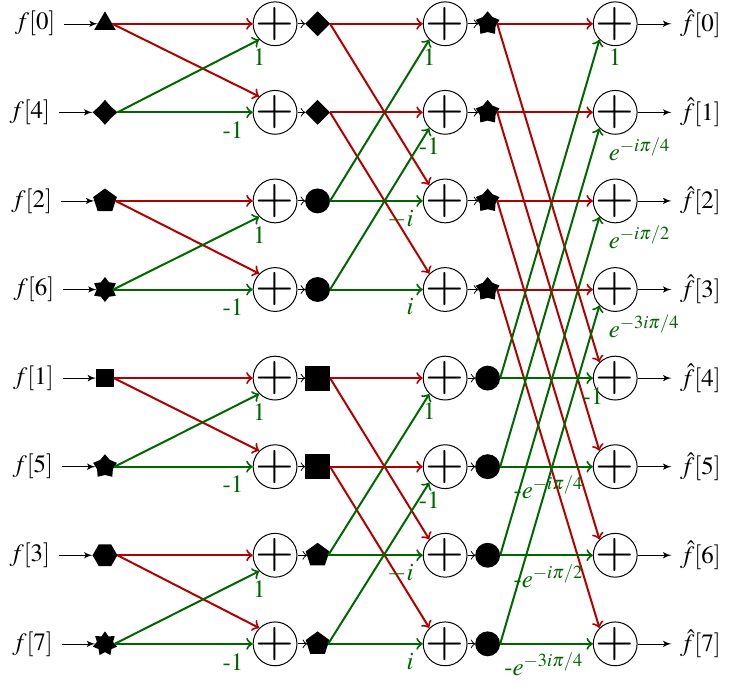
On voit qu’en procédant ainsi on a un ordonnement simple des sous tableaux. Puisque de toute manière il faudra procéder à une permutation du tableau, il est intéressant de le faire avant le calcul de la FFT.
- MSB et LSB sont les acronymes de Most Significant Bit et Least Significant Bit. Dans un nombre représenté sur bits, le MSB est donc le bit qui porte l’information sur la puissance de 2 la plus élevée () alors que le LSB porte l’information sur la puissance de 2 la plus faible (). Concrètement le MSB est le bit le plus à gauche de la représentation binaire d’un nombre, alors que le LSB est le plus à droite.↩
Calculer la permutation inverse des bits
Il faut donc commencer par être en mesure de calculer la permutation. Il est possible de réaliser la permutation en place simplement une fois que l’on sait quels éléments échanger. Plusieurs méthodes existent pour effectuer la permutation, et une recherche dans Google Scholar vous donnera un aperçu de la richesse des approches.
Nous pouvons utiliser une petite astuce ici: puisque nous traitons uniquement des tableaux dont la taille est une puissance de 2, on peut écrire la taille ainsi : . Cela signifie que les indices peuvent être stockés sur bits. On peut alors simplement calculer l’indice permuté via des opérations binaires. Par exemple si alors l’indice pourrait être représenté ainsi :
1100011101.
On peut séparer le processus d’inversion en plusieurs étapes. Dans un premier temps on échange les 5 bits les plus significatifs et les 5 bits les moins significatifs. Ensuite sur chacun des demi-mots on inverse les deux bits les plus significatifs et les deux bits les moins significatifs (les bits centraux ne changent pas). Enfin sur les mots de deux bits que l’on vient d’échanger, on échange le bit le plus significatif et le bit le moins significatif.
Un exemple d’implémentation serait le suivant :
bit_reverse(::Val{10}, num) = begin
num = ((num&0x3e0)>>5)|((num&0x01f)<<5)
num = ((num&0x318)>>3)|(num&0x084)|((num&0x063)<<3)
((num&0x252)>>1)|(num&0x084)|((num&0x129)<<1)
end
Un algorithme équivalent peut être appliqué pour toutes les valeurs de , il faut simplement faire attention à ne plus modifier les bits centraux quand on a un nombre impair de bits dans un demi-mot. Dans ce qui suit il y a un exemple pour plusieurs longueurs de mots.
bit_reverse(::Val{64}, num) = bit_reverse(Val(32), (num&0xffffffff00000000)>>32)|(bit_reverse(Val(32), num&0x00000000ffffffff)<<32)
bit_reverse(::Val{32}, num) = bit_reverse(Val(16), (num&0xffff0000)>>16)|(bit_reverse(Val(16), num&0x0000ffff)<<16)
bit_reverse(::Val{16}, num) = bit_reverse(Val(8), (num&0xff00)>>8)|(bit_reverse(Val(8), num&0x00ff)<<8)
bit_reverse(::Val{8}, num) = bit_reverse(Val(4), (num&0xf0)>>4)|(bit_reverse(Val(4), num&0x0f)<<4)
bit_reverse(::Val{4}, num) =bit_reverse(Val(2), (num&0xc)>>2)|(bit_reverse(Val(2), num&0x3)<<2)
bit_reverse(::Val{3}, num) = ((num&0x1)<<2)|((num&0x4)>>2)|(num&0x2)
bit_reverse(::Val{2}, num) = ((num&0x2)>>1 )|((num&0x1)<<1)
bit_reverse(::Val{1}, num) = num
On peut ensuite faire la permutation à proprement parler. L’algorithme est relativement simple : il suffit d’itérer sur le tableau, calculer l’indice inversé de l’indice courant et réaliser l’inversion. La seule subtilité est qu’il ne faut réaliser l’inversion qu’une fois par indice du tableau, donc on discrimine en ne réalisant l’inversion que si l’indice courant est inférieur à l’indice inversé.
function reverse_bit_order!(X, order)
N = length(X)
for i in 0:(N-1)
j = bit_reverse(order, i)
if i<j
X[i+1],X[j+1]=X[j+1],X[i+1]
end
end
X
end
Ma seconde FFT
Nous sommes maintenant suffisamment équipés pour nous lancer dans une seconde implémentation de la FFT. La première étape sera de calculer la permutation de bits inverse. Ensuite on pourra effectuer le calcul de la transformée de Fourier en suivant le schéma montré précédemment. Pour ce faire on stockera la taille des sous tableaux et le nombre de cases dans le tableau global qui séparent deux éléments de même indices dans les sous-tableaux. L’implémentation peut se faire ainsi :
function my_fft_2(x)
N = length(x)
order = Int(log2(N))
@inbounds reverse_bit_order!(x, Val(order))
n₁ = 0
n₂ = 1
for i=1:order # i done le numéro de la colonne dans lequel on se trouve.
n₁ = n₂ # n₁ = 2ⁱ⁻¹
n₂ *= 2 # n₂ = 2ⁱ
step_angle = -2π/n₂
angle = 0
for j=1:n₁ # j est l'indice dans Xᵉ et Xᵒ
factors = exp(im*angle) # z = exp(-2im*π*(j-1)/n₂)
angle += step_angle # a = -2π*(j+1)/n₂
# On combine l'élément j de chaque groupe de sous-tableaux
for k=j:n₂:N
@inbounds x[k], x[k+n₁] = x[k] + factors * x[k+n₁], x[k] - factors * x[k+n₁]
end
end
end
x
end
Il y a deux petites subtilités dues à Julia : les tableaux commencent leur numérotation à 1, et on utilise la macro @inbounds pour accélérer un peu le code en désactivant les vérifications de débordement de tableaux.
On peut à nouveau mesurer les performances de cette implémentation. Pour que la comparaison reste juste, il faut utiliser la fonction fft! et non plus fft, car elle travaille en place.
@benchmark fft!(a) setup=(a = rand(1024) |> complex)
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 23.212 μs … 16.917 ms ┊ GC (min … max): 0.00% … 47.76%
Time (median): 27.064 μs ┊ GC (median): 0.00%
Time (mean ± σ): 30.849 μs ± 169.018 μs ┊ GC (mean ± σ): 2.62% ± 0.48%
▆█▁▂
▄▇████▇▄▅▄▄▆▅▄▅▄▅▄▄▃▄▄▃▂▂▂▂▂▁▂▂▁▁▁▁▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂
23.2 μs Histogram: frequency by time 52.2 μs <
Memory estimate: 1.86 KiB, allocs estimate: 30.
@benchmark my_fft_2(a) setup=(a = rand(1024) .|> complex)
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 54.781 μs … 139.275 μs ┊ GC (min … max): 0.00% … 0.00%
Time (median): 57.969 μs ┊ GC (median): 0.00%
Time (mean ± σ): 63.386 μs ± 11.620 μs ┊ GC (mean ± σ): 0.00% ± 0.00%
▄ ▃█▁▁▄ ▃ ▃▂ ▃ ▂▂ ▁ ▁ ▁
█▇████████████████▇▇██▇▆▆██▇▇▆▇█▆▅▆▆▆█▆▆▆▆▆▆▇▆▆▄▆▆▅▄▆▅▅▆▆▇██ █
54.8 μs Histogram: log(frequency) by time 109 μs <
Memory estimate: 0 bytes, allocs estimate: 0.
On a significativement amélioré notre temps d’exécution et notre empreinte mémoire. On peut voir qu’il y a zéro octet alloué (cela signifie que le compilateur n’a pas besoin de stocker les quelques variables intermédiaires en RAM), et que le temps d’exécution se rapproche de celui de l’implémentation de référence.
Le cas particulier d'un signal réel
Jusqu’ici nous avons raisonné sur des signaux complexes, qui utilisent deux flottants pour le stockage. Cependant dans de nombreuses situations on travaille avec des signaux à valeur réelle. Or dans le cas d’un signal réel, on sait que vérifie . Cela signifie que la moitié des valeurs que l’on calcule est redondante. Bien que l’on calcule la transformée de Fourier d’un signal réel, le résultat peut être un nombre complexe. Afin d’économiser de l’espace de stockage, on peut penser à utiliser cette moitié de tableau pour stocker les nombres complexes. Pour cela deux propriétés vont nous aider.
Propriété 1 : Calculer la transformée de Fourier de deux fonctions réelles en même temps
Si l’on a deux signaux réels et , on peut définir le signal complexe . On a alors :
On peut remarquer que
En combinant les deux on a
Propriété 2 : Calculer la transformée de Fourier d’une seule fonction
L’idée est d’utiliser la propriété précédente en utilisant le signal des éléments pairs et celui des éléments impairs. Autrement dit pour on a .
On a alors:
On peut recombiner les deux transformées partielles. Pour :
En utilisant la première propriété, on a alors :
Calcul en place
Le tableau , qui est présenté précédemment, est à valeurs complexes. Cependant le signal d’entrée est à valeurs réelles et deux fois plus long. L’astuce est donc d’utiliser deux cases du tableau initial pour stocker un élément complexe de . Il est utile de poser les calculs avec nombres complexes avant de commencer à écrire du code. Pour le cœur de la FFT, si on note le tableau à l’étape de la boucle principale, on a :
Avec l’organisation que l’on choisit, il suffira de remplacer par et par . On note que l’on pourra également remplacer par ou encore mieux .
La dernière étape est le recombinaison de pour trouver le résultat final. La formule de la propriété 2 se ré-écrit après un calcul désagréable mais peu compliqué:
Il y a un cas particulier où cette formule ne fonctionne pas : quand on sort du tableau qui ne contient que éléments. Cependant on peut utiliser la symétrie de la Transformée de Fourier pour voir que . Le cas se simplifie alors énormément :
Pour effectuer le calcul en place, il est utile d’être en mesure de calculer au même moment où on calcule . En réutilisant les résultats précédents et le fait que , on trouve :
Après ce petit moment désagréable, nous sommes prêts à implémenter une nouvelle version de la FFT !
Une FFT pour les réels
Puisque le calcul effectif de la FFT se fait sur un tableau qui fait la moitié de la taille du tableau d’entrée, on a besoin d’une fonction pour calculer l’indice inversé sur 9 bits pour pouvoir continuer à tester sur 1024 points.
bit_reverse(::Val{9}, num) = begin
num = ((num&0x1e0)>>5)|(num&0x010)|((num&0x00f)<<5)
num = ((num&0x18c)>>2)|(num&0x010)|((num&0x063)<<2)
((num&0x14a)>>1)|(num&0x010)|((num&0x0a5)<<1)
end
Pour compléter les autres méthode de bit_reverse on peut utiliser les implémentations suivantes :
bit_reverse(::Val{31}, num) = begin
bit_reverse(Val(15), num&0x7fff0000>>16)| (num&0x00008000) |(bit_reverse(Val(7),num&0x00007fff)<<16)
end
bit_reverse(::Val{15}, num) = bit_reverse(Val(7), (num&0x7f00)>>8)| (num&0x0080)|(bit_reverse(Val(7),num&0x007f)<<8)
bit_reverse(::Val{7}, num) = bit_reverse(Val(3), (num&0x70)>>4 )| (num&0x08) |(bit_reverse(Val(3), num&0x07)<<4)
Pour tenir compte des spécificités de la représentation des complexes que l’on utilise, on implémente une nouvelle version de reverse_bit_order.
function reverse_bit_order_double!(x, order)
N = length(x)
for i in 0:(N-1)
j = bit_reverse(order, i)
if i<j
# swap real part
x[2*i+1],x[2*j+1]=x[2*j+1],x[2*i+1]
# swap imaginary part
x[2*i+2],x[2*j+2]=x[2*j+2],x[2*i+2]
end
end
x
end
Ce qui mène à la nouvelle implémentation de la FFT.
function my_fft_3(x)
N = length(x) ÷ 2
order = Int(log2(N))
@inbounds reverse_bit_order_double!(x, Val(order))
n₁ = 0
n₂ = 1
for i=1:order # i done le numéro de la colonne dans lequel on se trouve.
n₁ = n₂ # n₁ = 2ⁱ⁻¹
n₂ *= 2 # n₂ = 2ⁱ
step_angle = -2π/n₂
angle = 0
for j=1:n₁ # j est l'indice dans Xᵉ et Xᵒ
re_factor = cos(angle)
im_factor = sin(angle)
angle += step_angle # a = -2π*j/n₂
# On combine l'élement j de chaque groupe de sous-tableaux
@inbounds for k=j:n₂:N
re_xₑ = x[2*k-1]
im_xₑ = x[2*k]
re_xₒ = x[2*(k+n₁)-1]
im_xₒ = x[2*(k+n₁)]
x[2*k-1] = re_xₑ + re_factor*re_xₒ - im_factor*im_xₒ
x[2*k] = im_xₑ + im_factor*re_xₒ + re_factor*im_xₒ
x[2*(k+n₁)-1] = re_xₑ - re_factor*re_xₒ + im_factor*im_xₒ
x[2*(k+n₁)] = im_xₑ - im_factor*re_xₒ - re_factor*im_xₒ
end
end
end
# On construit la version finale de la TF
# N la moitié de la taille de x
# Cas particulier n=0
x[1] = x[1] + x[2]
x[2] = 0
step_angle = -π/N
angle = step_angle
@inbounds for n=1:(N÷2)
re_factor = cos(angle)
im_factor = sin(angle)
re_h = x[2*n+1]
im_h = x[2*n+2]
re_h_sym = x[2*(N-n)+1]
im_h_sym = x[2*(N-n)+2]
x[2*n+1] = 1/2*(re_h + re_h_sym + im_h*re_factor + re_h*im_factor + im_h_sym*re_factor - re_h_sym*im_factor)
x[2*n+2] = 1/2*(im_h - im_h_sym - re_h*re_factor + im_h*im_factor + re_h_sym*re_factor + im_h_sym*im_factor)
x[2*(N-n)+1] = 1/2*(re_h_sym + re_h - im_h_sym*re_factor + re_h_sym*im_factor - im_h*re_factor - re_h*im_factor)
x[2*(N-n)+2] = 1/2*(im_h_sym - im_h + re_h_sym*re_factor + im_h_sym*im_factor - re_h*re_factor + im_h*im_factor)
angle += step_angle
end
x
end
On peut maintenant vérifier les performances de la nouvelle implémentation :
@benchmark fft!(x) setup=(x = rand(1024) .|> complex)
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 23.762 μs … 17.229 ms ┊ GC (min … max): 0.00% … 51.97%
Time (median): 27.817 μs ┊ GC (median): 0.00%
Time (mean ± σ): 32.823 μs ± 239.264 μs ┊ GC (mean ± σ): 5.20% ± 0.71%
▅▂▆█
▂▆█████▆▆▅▅▆▄▆▇▅▄▃▅▄▄▄▅▄▃▂▂▂▂▂▁▁▂▁▁▁▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂
23.8 μs Histogram: frequency by time 50.2 μs <
Memory estimate: 1.86 KiB, allocs estimate: 30.
@benchmark my_fft_3(x) setup=(x = rand(1024))
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 30.631 μs … 99.197 μs ┊ GC (min … max): 0.00% … 0.00%
Time (median): 31.178 μs ┊ GC (median): 0.00%
Time (mean ± σ): 33.957 μs ± 5.907 μs ┊ GC (mean ± σ): 0.00% ± 0.00%
▆█ ▄▆ ▄ ▄▁ ▃ ▂▁ ▂ ▃▃ ▁▂ ▁ ▁ ▂
██▇██▇▇█▇▅██▅▇█▇▆▇██▇▆▇█▇▆▆▆██▆▆▆▆██▆▅▄▅▅█▇▆▆▅▆▅▆█▅▅▅▅▅▃▅▁▆ █
30.6 μs Histogram: log(frequency) by time 57.7 μs <
Memory estimate: 0 bytes, allocs estimate: 0.
C’est un très bon résultat !
Optimisation des fonctions trigonométriques
Si on analyse l’exécution de my_fft_3 à l’aide du profiler de Julia, on s’aperçoit que la plus grosse partie du temps est passée à calculer des fonctions trigonométriques et à créer les objets StepRange utilisés dans les boucles for. Le second problème peut être contourné facilement en utilisant des boucles while. Pour le premier, au détour de Numerical Recipes on peut lire (section 5.4 "Recurrence Relations and Clenshaw’s Recurrence Formula", page 219 de la troisième édition):
If your program’s running time is dominated by evaluating trigonometric functions, you are probably doing something wrong. Trig functions whose arguments form a linear sequence , are efficiently calculated by the recurrence
Where and are the precomputed coefficients
On peut montrer cela en utilisant les identitées trigonométriques classiques :
Et avec , on a directement la seconde formule.
Cette relation présente également des intérêts en termes de stabilité numérique. On peut directement implémenter une version finale de notre FFT en utilisant ces relations.
function my_fft_4(x)
N = length(x) ÷ 2
order = Int(log2(N))
@inbounds reverse_bit_order_double!(x, Val(order))
n₁ = 0
n₂ = 1
i=1
while i<=order # i done le numéro de la colonne dans lequel on se trouve.
n₁ = n₂ # n₁ = 2ⁱ⁻¹
n₂ *= 2 # n₂ = 2ⁱ
step_angle = -2π/n₂
α = 2sin(step_angle/2)^2
β = sin(step_angle)
cj = 1
sj = 0
j = 1
while j<=n₁ # j est l'indice dans Xᵉ et Xᵒ
# On combine l'élement j de chaque groupe de sous-tableaux
k = j
@inbounds while k<=N
re_xₑ = x[2*k-1]
im_xₑ = x[2*k]
re_xₒ = x[2*(k+n₁)-1]
im_xₒ = x[2*(k+n₁)]
x[2*k-1] = re_xₑ + cj*re_xₒ - sj*im_xₒ
x[2*k] = im_xₑ + sj*re_xₒ + cj*im_xₒ
x[2*(k+n₁)-1] = re_xₑ - cj*re_xₒ + sj*im_xₒ
x[2*(k+n₁)] = im_xₑ - sj*re_xₒ - cj*im_xₒ
k += n₂
end
# On calcule le prochain cosinus et le prochain sinus.
cj, sj = cj - (α*cj + β*sj), sj - (α*sj-β*cj)
j+=1
end
i += 1
end
# On construit la version finale de la TF
# N la moitié de la taille de x
# Cas particulier n=0
x[1] = x[1] + x[2]
x[2] = 0
step_angle = -π/N
α = 2sin(step_angle/2)^2
β = sin(step_angle)
cj = 1
sj = 0
j = 1
@inbounds while j<=(N÷2)
# On calcule les cosinus et sinus avant le calcul principal ici pour compenser la première
# étape de la boucle que l'on a sautée.
cj, sj = cj - (α*cj + β*sj), sj - (α*sj-β*cj)
re_h = x[2*j+1]
im_h = x[2*j+2]
re_h_sym = x[2*(N-j)+1]
im_h_sym = x[2*(N-j)+2]
x[2*j+1] = 1/2*(re_h + re_h_sym + im_h*cj + re_h*sj + im_h_sym*cj - re_h_sym*sj)
x[2*j+2] = 1/2*(im_h - im_h_sym - re_h*cj + im_h*sj + re_h_sym*cj + im_h_sym*sj)
x[2*(N-j)+1] = 1/2*(re_h_sym + re_h - im_h_sym*cj + re_h_sym*sj - im_h*cj - re_h*sj)
x[2*(N-j)+2] = 1/2*(im_h_sym - im_h + re_h_sym*cj + im_h_sym*sj - re_h*cj + im_h*sj)
j += 1
end
x
end
On peut vérifier que l’on obtient toujours le bon résultat :
let
a = rand(1024)
b = fft(a)
c = my_fft_4(a)
real.(b[1:end÷2]) ≈ c[1:2:end] && imag.(b[1:end÷2]) ≈ c[2:2:end]
end
true
En termes de performances, on est enfin parvenu à dépasser l’implémentation de référence !
@benchmark fft!(x) setup=(x = rand(1024) .|> complex)
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 24.028 μs … 16.866 ms ┊ GC (min … max): 0.00% … 49.13%
Time (median): 28.186 μs ┊ GC (median): 0.00%
Time (mean ± σ): 32.935 μs ± 237.037 μs ┊ GC (mean ± σ): 5.02% ± 0.70%
▂█▁
▁▂▃▄███▄▅▅▃▃▄▅▃▃▄▄▃▃▃▃▃▃▃▃▃▃▂▂▂▂▂▂▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁ ▂
24 μs Histogram: frequency by time 46.1 μs <
Memory estimate: 1.86 KiB, allocs estimate: 30.
@benchmark my_fft_4(x) setup=(x = rand(1024))
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 15.863 μs … 57.225 μs ┊ GC (min … max): 0.00% … 0.00%
Time (median): 17.397 μs ┊ GC (median): 0.00%
Time (mean ± σ): 18.580 μs ± 3.296 μs ┊ GC (mean ± σ): 0.00% ± 0.00%
▃ ▄█ ▇ ▃▃ ▄▁ ▁▂ ▅▂ ▄ ▂ ▂ ▂ ▁ ▂
█▁██████▆██▇▅██▅▆██▆▆▆██▅▅▅▇██▇▇▇▆█▇▆▇▇▆▇█▆▆▅▅▆▆▆█▅▅▅▅▅▅▅▅█ █
15.9 μs Histogram: log(frequency) by time 30.7 μs <
Memory estimate: 0 bytes, allocs estimate: 0.
Si l’on compare les différentes implémentations proposées dans ce tutoriel ainsi que les deux implémentations de référence, puis que l’on trace les valeurs médianes de temps d’exécution, d’empreinte mémoire et de nombre d’allocations, on obtient le graphe suivant:
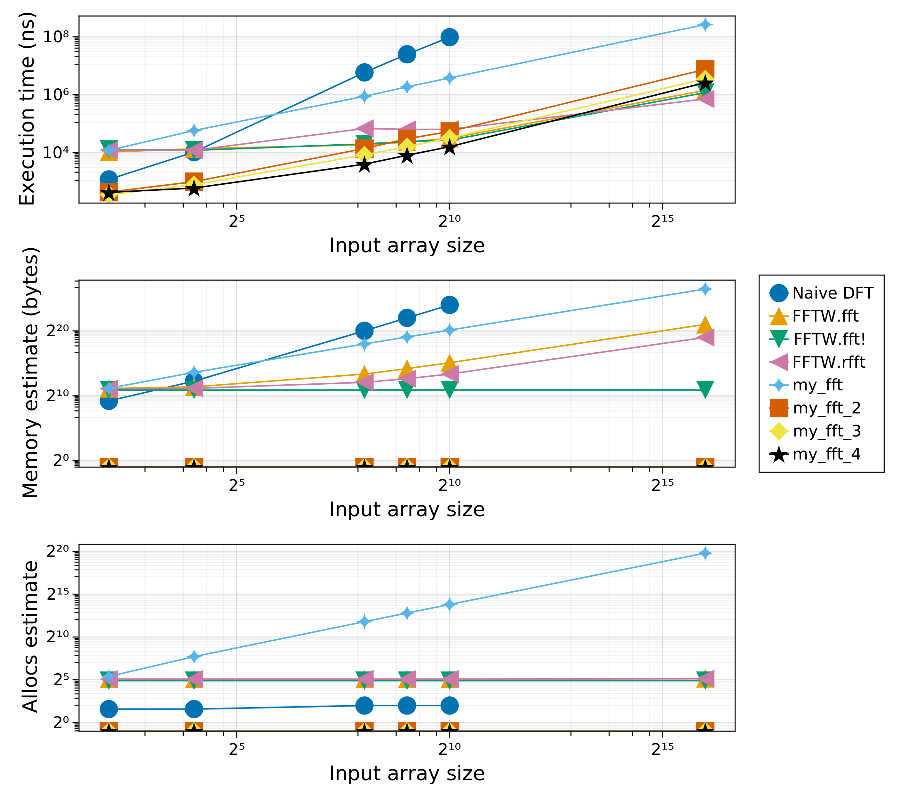
J’ai ajouté la fonction FFTW.rfft qui est censée être optimisée pour les réels. On voit qu’en réalité, à moins de travailler sur de très gros tableaux, elle n’apporte pas énormément de performances.
On peut voir que les dernières versions de l’algorithme se défendent très bien en termes de nombre d’allocations et d’empreinte mémoire. Pour ce qui est du temps d’exécution, l’implémentation de référence finit par être plus rapide sur les très gros tableaux.
Comment peut-on expliquer ces différences, en particulier entre notre dernière implémentation et l’implémentation dans FFTW ? Quelques éléments de réponse :
- FFTW résout un problème bien plus large. En effet notre implémentation est "naïve" par exemple dans le sens où elle ne peut travailler que sur des tableaux d’entrée dont la taille est une puissance de deux. Et encore, seulement ceux pour laquelle on s’est donné la peine d’implémenter une méthode de la fonction
bit_reverse. Le problème de la permutation de bits inverse est un peu plus compliqué à résoudre dans le cas général. De plus FFTW assure une bonne exécution sur de nombreux types d’architectures, propose des transformées de Fourier discrètes en multiples dimensions etc… Si le sujet vous intéresse, je vous conseille cet article1 qui présente le fonctionnement interne de FFTW. - La représentation des nombres complexes joue en notre faveur. En effet on évite à notre implémentation de devoir faire la moindre conversion, cela se voit en particulier dans les codes de test où l’on se charge de récupérer la partie réelle et la partie imaginaire de la transformée :
real.(b[1:end÷2]) ≈ c[1:2:end] && imag.(b[1:end÷2]) ≈ c[2:2:end]
- Notre algorithme n’a pas été pensé avec la stabilité numérique en tête. C’est un aspect qui pourrait encore être amélioré. De même, nous ne l’avons pas testé sur autre chose que du bruit. Le bloc suivant présente cependant quelques tests qui laissent penser qu’il "se comporte bien" pour quelques fonctions de test.
function test_signal(s)
b = fft(s)
c = my_fft_7_5(s)
real.(b[1:end÷2]) ≈ c[1:2:end] && imag.(b[1:end÷2]) ≈ c[2:2:end]
end
let
t = range(-10, 10; length=1024)
y = @. exp(-t^2)
noise = rand(1024)
test_signal(y .+ noise)
end
true
let
t = range(-10, 10; length=1024)
y = @. sin(t)
noise = rand(1024)
test_signal(y .+ noise)
end
true
Ces simplifications et cas particuliers permettent à notre implémentation de gagner fortement en rapidité. Cela rend d’autant plus remarquable l’implémentation de FFTW qui s’en sort tout de même très bien !
- Frigo, Matteo & Johnson, S.G.. (2005). The Design and implementation of FFTW3. Proceedings of the IEEE. 93. 216 - 231. 10.1109/JPROC.2004.840301.↩