Dans ce tutoriel, nous allons nous fixer pour but de calculer numériquement n’importe quelle intégrale. Pour illustrer ce tutoriel, nous allons nous baser sur le calcul de l’intégrale de la fonction qui à associe sur l’intervalle . Nous allons alors trouver des algorithmes permettant d’approcher le mieux possible la valeur de son intégrale.
Bien sûr, puisque nous ne connaissons pas la valeur de cette intégrale, nous ne pourrons pas vérifier que les algorithmes vus donnent bien le bon résultat. Nous allons alors les vérifier sur une autre intégrale, à savoir celle de la fonction cosinus sur l’intervalle .
Présentation du problème
Nous voulons calculer numériquement l’intégrale de , le problème étant que nous n’en connaissons pas de primitive explicite. La situation est mauvaise, et pour le moment, nous n’avons aucune idée de comment calculer cette intégrale.
Changeons d’aire
Pourtant, un simple changement de point de vue rend ce problème plus simple. Plaçons-nous d’un point de vue graphique en nous rappelant que l’intégrale d’une fonction correspond à l’aire sous sa courbe représentative. Ainsi, calculer l’intégrale d’une fonction revient à trouver la surface sous sa courbe représentative. La question qui vient alors est la suivante.
Comment calculer cette aire ?
Nous pourrions tourner en rond en disant qu’il s’agit de l’intégrale de la fonction associée à cette courbe, mais ce ne serait pas très productif…
Il nous faut ruser. Nous avons le graphe de la fonction à notre disposition, nous devrions alors être capable d’en tirer quelque chose et de calculer l’aire voulue. Bien sûr l’histoire n’est pas aussi simple et obtenir une valeur exacte de cette aire est compliqué.
Nous devrons nous contenter d’une valeur approchée de cette aire. Pour cela, nous allons approcher la courbe de notre fonction par la courbe d’une autre fonction, dont nous connaissons la valeur de l’aire. Dis comme ça, ça à l’air simple, mais encore faut-il savoir par quelle fonction nous allons l’approcher. Nous allons voir qu’il existe plusieurs manières de le faire. Certaines sont plus précises et permettent d’avoir une meilleure approximation en moins de calcul (bien sûr, tout cela dépend également de la forme de la fonction que l’on veut intégrer et de ce qu’on connaît d’elle).
Approximation de la courbe
Nous avons décidé d’approcher la courbe de notre fonction par la courbe d’une autre fonction dont nous connaissons l’intégrale. Il nous reste à trouver quelle fonction nous allons utiliser pour cela. Regardons la courbe représentative de la fonction, peut-être nous donnera-t-elle une idée.
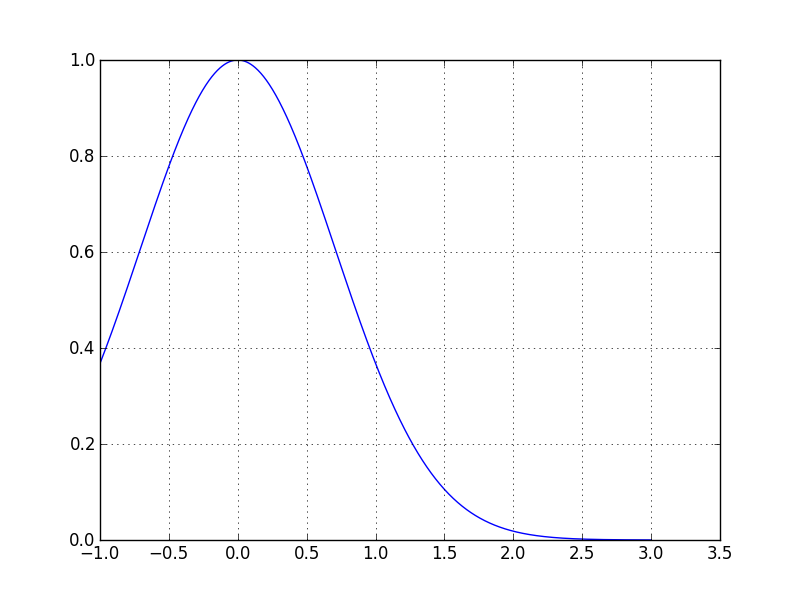
Trouver une fonction autre que dont la courbe approche suffisamment bien cette courbe semble compliqué. Là encore, il va nous falloir ruser.
Découpage de la fonction
Plutôt que de chercher une fonction qui approche sur tout l’intervalle, nous allons découper l’intervalle en plusieurs morceaux et approcher la fonction sur chacun des intervalles par une fonction différente. Le travail est alors plus facile.
Par exemple, pour intégrer de -1 à 3, on peut l’approcher par une fonction différente sur chaque intervalle de longueur 0,5. Le plus simple est de l’approcher par une fonction constante de manière à avoir à chaque fois l’aire d’un rectangle à calculer. On obtient alors cette approximation.
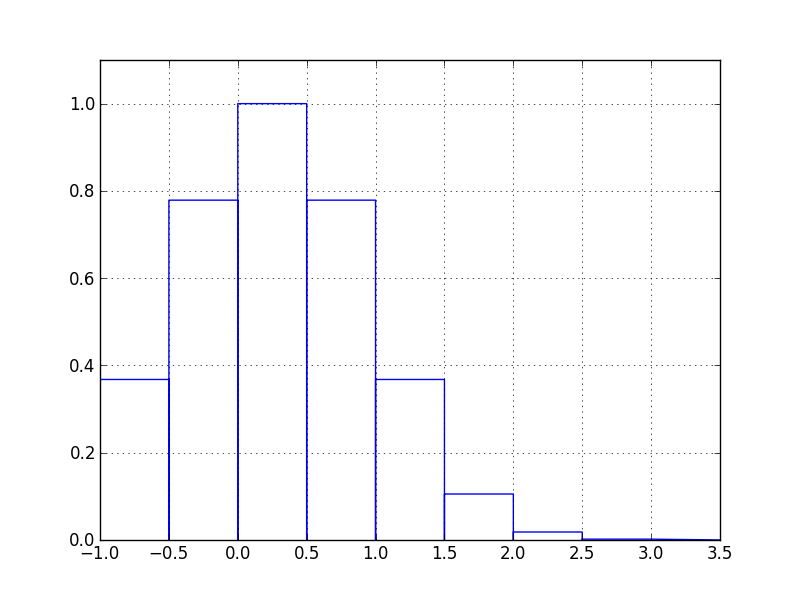
Quoi ? Mais ça n’approche pas bien du tout la courbe. Les aires seront beaucoup trop différentes.
C’est vrai que les deux courbes ne sont pas trop proches. Mais en diminuant la longueur des intervalles, les deux courbes sont de plus en plus proches, comme on peut le voir sur le graphe ci-dessous (en bleu la courbe représentative de la fonction et en vert les rectangles).
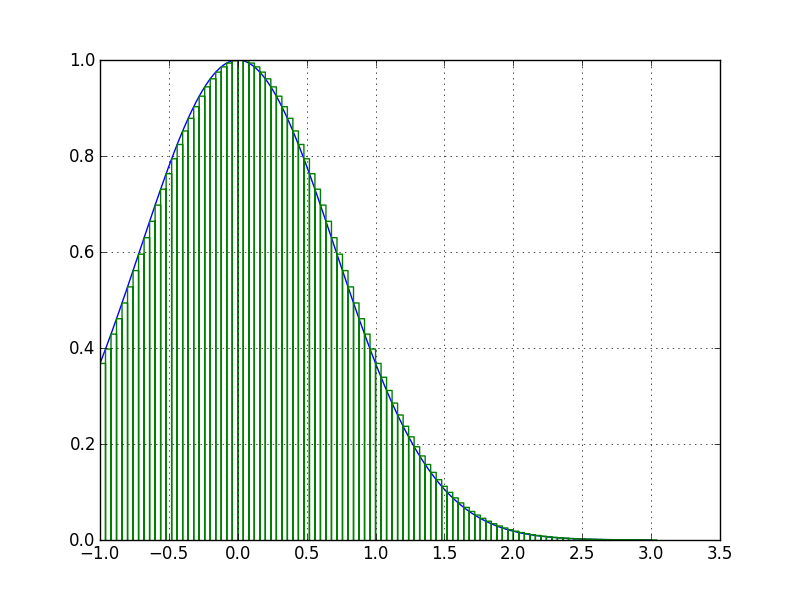
Calcul de l’aire
Il nous faut maintenant calculer l’aire approchée. On va séparer notre intervalle en 8 et calculer l’aire des 8 rectangles obtenus. On a que la largeur de chaque rectangle est . Il nous faut maintenant les hauteurs :
- la hauteur du premier rectangle est ;
- la hauteur du deuxième rectangle est ;
- la hauteur du troisième rectangle est .
En fait, la hauteur du kème rectangle est . On additionne ces différentes aires.
Le symbole introduit ici est le symbole de la somme. se lit comme « la somme pour allant de 0 à 10 des », c’est-à-dire comme
Formalisation
Maintenant que nous avons une méthode, il ne nous reste plus qu’à la formaliser. Considérons alors les fonctions continues sur l’intervalle . Cet intervalle étant un intervalle fermé borné, alors, d’après le théorème des bornes, l’image de par est un intervalle fermé borné. Ceci nous assure que ne « parte pas vers l’infini » (pour ne pas avoir de rectangle d’aire infinie).
Certaines fonctions ont des limites infinies et leur intégrale est quand même finie ( par exemple) mais nous n’allons pas en tenir compte ici.
Une fois que ceci est assuré, nous pouvons appliquer la méthode que nous avons trouvée. Rappelons-nous qu’elle consiste à faire deux choses.
- Diviser l’intervalle en petits intervalles de même longueur.
- Remplacer l’aire de sur ces intervalles par l’aire de petits rectangles.
Division de l’intervalle
Pour diviser en intervalles, posons pour tout entier de ,
On a ainsi une subdivision de notre intervalle. Les sont les abscisses des points de cette subdivision.
Nommons un peu tout ce que nous venons d’utiliser :
- est le nombres de tranches de la subdivision ;
- est le pas de la subdivision (c’est la distance entre deux points).
Les peuvent également être définis par récurrence :
Calcul de l’intégrale
Maintenant que nous avons subdivisé notre intervalle, nous pouvons utiliser la relation de Chasles pour remarquer ceci :
Il ne reste plus qu’à remplacer la fonction sur chacun des intervalles par une fonction constante.
On obtiendra alors une approximation de .
Pour correspondre à la méthode que nous avons utilisée, il faut . On a alors que l’aire de chaque rectangle est
L’intégrale d’une constante sur un intervalle est cette constante multipliée par la longueur de l’intervalle, donc
On peut maintenant passer à l’approximation de l’aire totale sous la courbe :
On peut sortir la constante de la somme et on obtient comme résultat final :
La méthode que nous venons de trouver porte un nom. Il s’agit de la méthode des rectangles qui consiste à remplacer la fonction sur chaque par une fonction constante. Notons qu nous aurions aussi pu choisir . On peut alors faire ces deux méthodes des rectangles :
- la méthode des rectangles à gauche où ;
- la méthode des rectangles à droite où .
La méthode des rectangles correspond aux sommes de Riemann qui peuvent être utilisées pour définir la notion d’intégration.
Algorithme et vérification
Maintenant que nous avons trouvé une formule, utilisons-la pour écrire un algorithme en Python. Écrivons la méthode des rectangles à gauche.
def rectangle(f, a, b, n):
somme = 0
pas = (b - a) / n
x = a
for i in range(0, n): # On calcule la somme des f(x_i)
somme += f(x)
x += pas
return somme * pas # On retourne cette somme fois le pas
Ici, rectangle prend en paramètre la fonction f à intégrer, les deux bornes d’intégration a et b et le nombre de tranches n à utiliser pour la subdivision.
Pour vérifier si notre algorithme fonctionne, utilisons le sur des fonctions dont nous connaissons l’intégrale. Par exemple,
On peut alors essayer de voir ce que donne rectangle(cos, 0, pi, 100). Diviser l’intervalle en 100 semble suffisant pour obtenir une bonne valeur. Nous obtenons 0,0314, associé à ce graphe.
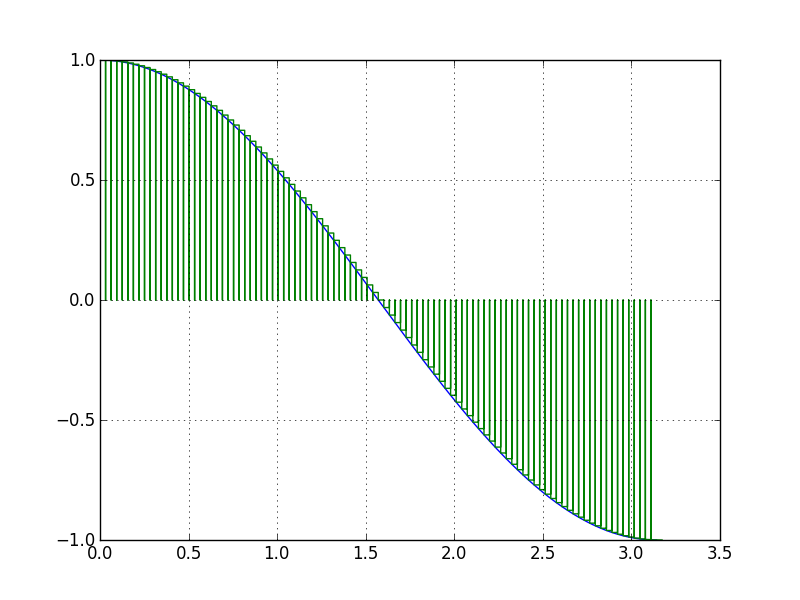
La méthode semble alors fonctionner. Mais ce petit test ne peut pas suffire à nous convaincre qu’elle donne des résultats satisfaisants dans tous les cas. Nous pouvons alors la tester sur d’autres fonctions pour voir ce qu’on obtient.
Reste à voir ce qu’elle donne sur notre exemple.
from math import exp
def f(x):
return exp(-(x*x))
print(rectangle(f, 0, 1, 100))
On obtient environ 0,749979.