Performance et précision - Calcul approché d'intégrales • Bibliothèque • Zeste de Savoir

Les pentes c’est dangereux
La méthode des trapèzes
Algorithme de la méthode des trapèzes

Les pentes c’est dangereux

Test de la méthode des rectangles

La méthode des rectangles semble fonctionner assez bien. Nous l’avons testé sur la fonction cosinus et en divisant l’intervalle en 100, nous avions obtenu un résultat vrai jusqu’à la première décimale. Mais qu’en est-il d’autres fonctions ? Le résultat est-il toujours aussi bon ?

Il paraît évident que si nous testons la méthode des rectangles sur une fonction constante, le résultat sera bon. En fait, dans ce cas, le résultat est exactement la valeur de l’intégrale et pas une valeur approchée. De même, si nous la testons sur une fonction en escalier, nous avons de bonnes chances d’obtenir un bon résultat (pourvu que le pas soit bien choisi).

Cependant, nous pouvons voir que si nous testons notre fonction sur une fonction qui croît rapidement par exemple, le résultat sera moins probant. Et plus la fonction croîtra vite, moins le résultat sera probant.

Augmenter la précision du résultat

Notre but est alors d’augmenter la précision de notre résultat. Pour cela, rappelons-nous du chapitre précédent. En diminuant le pas, nous augmentons la précision de notre résultat. En faisant de même ici, on devrait améliorer notre résultat.

Bien sûr, cette solution fonctionne, mais si l’on augmente encore la pente, on se retrouve encore avec une différence notable. De plus, augmenter le pas augmente également le temps de calcul. Sur certaines courbes, cette solution n’est pas viable. Il nous faut donc trouver une autre méthode pour gérer ce cas des fonctions à forte pente.

En fait, nos ordinateurs font des erreurs d’approximation lors des calculs, de sorte que si en théorie un pas infiniment petit est possible, en pratique, ça ne l’est pas. Pour plus d’informations à ce sujet, nous pouvons nous renseigner sur les erreurs de calcul des ordinateurs (voir cet article et celui-là).

La méthode des trapèzes

Principe de la méthode

La méthode des trapèzes consiste à remplacer la fonction $f$ sur chaque intervalle par une fonction qui sera affine. Pour qu’elle approche bien la courbe, les fonctions que nous allons utiliser sont toutes trouvées : pour chaque $x_k$ de la subdivision, nous allons prendre la fonction qui passe par les points $M_k(x_k, f(x_k))$ et $M_{k + 1}(x_{k + 1}, f(x_{k + 1}))$ .

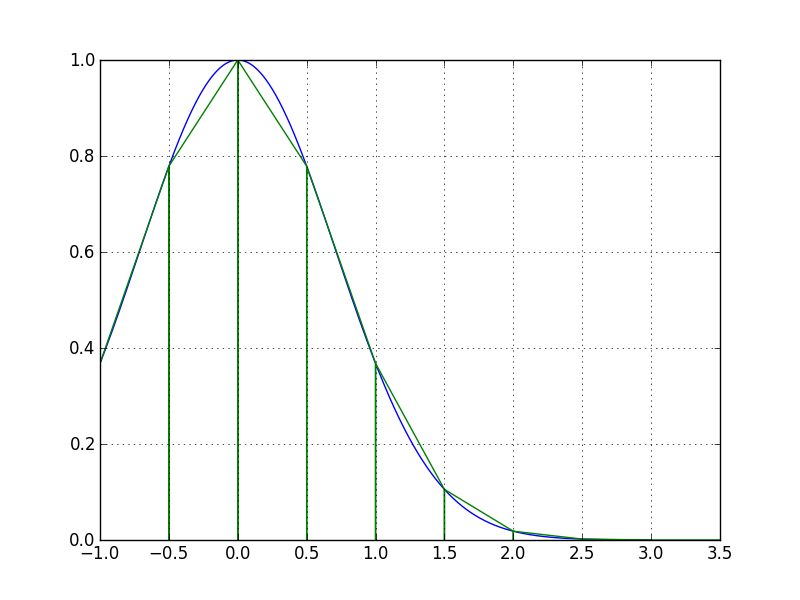
Avec des trapèzes, c’est mieux. — Avec des trapèzes c’est mieux.

Nous voyons qu’en approchant la courbe de notre fonction par des trapèzes, on s’en rapproche plus que lorsque l’on utilisait des rectangles. Sur cette fonction, la méthode des trapèzes donne une meilleure approximation que celle des rectangles.

Maintenant que nous avons vu les choses graphiquement, trouvons les fonctions $g_k$ correspondantes. On veut une fonction affine (donc de la forme $g_k(x) = cx + d$ ) telle que

\left\{ \begin{aligned} g_k(x_{k + 1}) &= f(x_{k + 2})\\ g_k(x_k) &= f(x_k) \end{aligned} \right..

Ces deux informations nous permettent de trouver la fonction. On a

g_k(x) = \frac{f(x_{k + 1}) - f(x_k)}{x_{k + 1} - x_k} (x - x_k) + f(x_k).

Calcul de l’intégrale

La connaissance des fonctions $g_k$ nous permet de calculer les aires $T_k$ des différents trapèzes :

T_k(f) = \int_{x_k}^{x_{k + 1}} g_k(t) \mathrm{d}t = \int_{x_k}^{x_{k + 1}} \frac{f(x_{k + 1}) - f(x_k)}{x_{k + 1} - x_k} (t - x_k) + f(x_k) \mathrm{d}t.

Nous pouvons nous amuser à calculer cette intégrale si nous le voulons (comment ça, ce n’est pas amusant), mais ce sera inutile. En effet, nous sommes malins. Et donc, nous préférons calculer l’aire du trapèze, plutôt que cette intégrale.

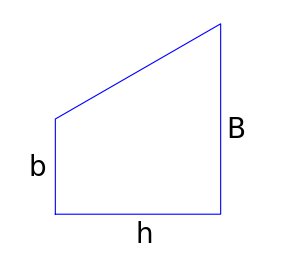
Pour ceux qui l’auraient oublié, l’aire d’un trapèze est : $h \frac{b + B}{2}$ (pour la retrouver, on peut découper le trapèze en un rectangle et un triangle rectangle).

On a donc dans notre cas :

$h = x_{k + 1} - x_k$  ;
$b = f(x_k)$  ;
$B = f(x_{k + 1})$ .

Et donc :

T_k(f) = x_{k + 1} - x_k \frac{f(x_k) + f(x_{k + 1})}{2}.

Et comme pour la méthode des rectangles, puisque $x_{k + 1} - x_k = \delta$ , on a :

T_k(f) = \delta \frac{f(x_k) + f(x_{k + 1})}{2}.

Nous pouvons maintenant approcher $I(f)$  :

I(f) \approx \sum_{k = 0}^{n - 1} T_k(f) = \sum_{k = 0}^{n - 1} \delta \frac{f(x_k) + f(x_{k + 1})}{2}.

On peut sortir la constante $\frac{\delta}{2}$ de la somme :

I(f) \approx \frac{\delta}{2} \sum_{k = 0}^{n - 1} f(x_k) + f(x_{k + 1}).

On remarque alors que tous les $x_k$ sont comptés deux fois sauf le premier ( $x_0$ ) et le dernier ( $x_n$ ). Donc :

I(f) \approx \frac{\delta}{2} \left( f(x_0) + f(x_n) + 2\sum_{k = 1}^{n - 1} f(x_k) \right).

Et finalement, en multipliant toute la somme par le $2$ , on obtient

\boxed{I(f) \approx \delta \left( \frac{f(x_0) + f(x_n)}{2} + \sum_{k = 1}^{n - 1} f(x_k) \right)}.

Algorithme de la méthode des trapèzes

Écrivons cet algorithme en Python.

def trapèze(f, a, b, n):
    somme = (f(a) + f(b)) / 2   # On initialise la somme à (f(a) + f(b)) / 2
    pas = (b - a) / n
    x = a + pas                 # La somme commence à x_1 
    for i in range(1, n):       # On calcule la somme des f(x_i)
        somme += f(x)
        x += pas
    return somme * pas          # On retourne cette somme fois le pas

Vérifions qu’il fonctionne en vérifiant (comme pour la méthode des rectangles) qu’il nous donne un résultat proche de 0 pour l’intégrale de 0 à $\pi$ de la fonction cosinus. En découpant l’intervalle en 100 (donc avec trapèze(cos, 0, pi, 100)) on obtient un résultat de l’ordre de -10^-15 là où avec la méthode des rectangles on obtenait un résultat de l’ordre de 10^-2. La méthode des trapèzes nous donne un résultat beaucoup plus précis.

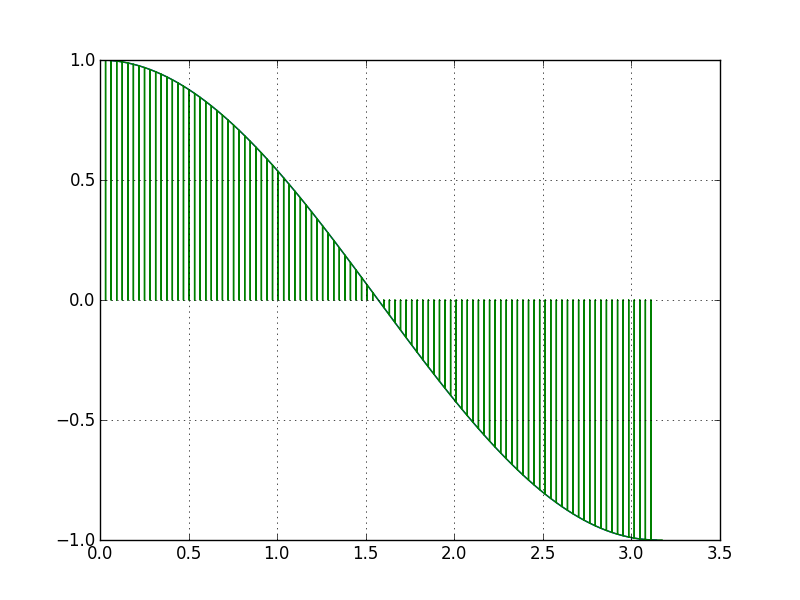
La méthode des trapèzes sur la fonction cosinus.

Nous voyons qu’en effet, la courbe de la fonction est plus épousée par les trapèzes que par les rectangles.

Voyons voir ce qu’on obtient sur notre exemple.

print(trapèze(f, 0, 1, 100))

On obtient environ 0,746818.