À première vue, le calcul avec les flottants est très similaire à celui avec les réels. Cependant, de nombreuses différences apparaissent en regardant de plus près, causées notamment par la nécessité de faire des arrondis.
Dans cette partie, nous verrons tout d’abord ce qu’il se passe pour les opérations élémentaires, effectuées individuellement, avant de voir les phénomènes apparaissant quand de multiples opérations s’enchaînent. Ensuite, nous étudierons quelques cas problématiques, et nous présenterons enfin un exemple d’algorithme de sommation astucieux.
- Opérations élémentaires
- Enchaînements d'opérations
- Exemples de situations problématiques
- Exemple d'algorithme intelligent : la sommation compensée de Kahan
Opérations élémentaires
La plupart des réels ne sont pas représentables exactement par un flottant, et subissent donc un arrondi lors de leur conversion. La nécessité d’arrondir rend les opérations, même les plus simples comme l’addition, non triviales. La manière précise de les effectuer est définie dans la norme IEEE 754.
Déroulement d’une opération élémentaire
Pour de nombreuses opérations élémentaires (listées plus loin), la norme dicte comment il faut les effectuer. Dans le cas où ces opérations sont effectuées individuellement, la procédure est la suivante :
- convertir les opérandes en flottant, comme expliqué dans la partie précédente ;
- effectuer l’opération sur les opérandes arrondies ;
- convertir le résultat en flottant, comme si le calcul avait été effectué de manière exacte ;
- stocker le résultat (affectation à une variable par exemple).
Ainsi, lorsqu’une opération simple est effectuée, on n’obtient pas simplement le résultat, mais l’arrondi du résultat exact de l’opération effectuée sur les opérandes arrondis. Il y a donc déjà trois opérations d’arrondi pour la moindre addition !
Les opérations élémentaires devant nécessairement arrondir correctement sont les suivantes : addition, soustraction, multiplication, division, multiply-accumulate1 et racine carrée.
La norme recommande aussi aux langages de proposer de nombreuses autres fonctions arrondissant correctement, telles que l’exponentielle, le logarithme, la puissance, la racine n-ième, les fonctions trigonométriques, hyperboliques et leurs réciproques.
Les comportements d’arrondis provoquent différents phénomènes indésirables lors des calculs avec les flottants.
Erreurs d’arrondi
Lors d’un calcul, le résultat n’est généralement pas l’arrondi du résultat effectué avec les opérandes réels, à cause des opérations d’arrondi qu’elles subissent. À cette erreur d’arrondi s’ajoute l’erreur d’arrondi sur le résultat.
Pour voir un effet concret de ces phénomènes, reprenons l’exemple de l’introduction, où nous avons vu que n’était pour l’ordinateur pas égal à .
>>> a = 0.1
>>> a
1.00000000000000006e-01
>>> b = 0.2
>>> b
2.00000000000000011e-01
>>> c = 0.1 + 0.2
>>> c
3.00000000000000044e-01
>>> d = 0.3
>>> d
2.99999999999999989e-01
En regardant les résultats ci-dessus, on voit tout de suite pourquoi l’ordinateur annonçait False lors de la comparaison ! L’arrondi de n’est pas le même que l’arrondi de l’addition des arrondis de et .
Il est possible de majorer l’erreur pour les opérations élémentaires. Nous allons le faire à titre d’exemple pour l’addition (qui est pareil que la soustraction). Prenons deux opérandes réelles et , qui subissent une erreur d’arrondi et respectivement. Après l’addition des opérandes arrondies, le résultat est arrondi au flottant le plus proche avec une erreur . Ainsi, la distance entre le résultat sur les réels et le résultat sur les flottants peut être majorée de la manière suivante :
En faisant l’application numérique avec les variables du code Python vu ci-avant, on trouve :
Ce qui est cohérent avec l’erreur de calcul effectivement obtenue, qui vaut environ .
Absorption
Les phénomènes d’absorption se produisent lorsque l’on additionne ou soustrait un nombre relativement petit à un nombre relativement grand. Dans ces conditions, un des opérandes absorbera l’autre : tout se passe comme ci l’opération n’avait pas eu lieu !
On peut voir le phénomène à l’œuvre dans l’exemple suivant, où l’on additionne un nombre de l’ordre du milliard avec un nombre de l’ordre du milliardième.
>>> a = 2**30 # a est grand
>>> b = 2**-27 # b est petit relativement à a
>>> a + b == a # absorption
True
Dans cet exemple, les deux flottants à additionner n’ont pas les mêmes exposants. Dans ce cas-là, l’addition s’effectue comme suit : les deux nombres sont d’abord mis au même exposant (le plus grand), puis seulement ensuite leurs significandes sont additionnés. La mise au même exposant consiste à multiplier le nombre par la puissance de deux nécessaire pour avoir le même exposant, et diviser dans le même temps le significande par le même nombre. Mathématiquement, l’opération laisse le nombre inchangé, mais c’est sans compter sur la précision limitée des flottants. En effet, diviser un nombre par une puissance de deux revient à décaler ses bits vers la droite. Si on décale trop loin, des bits vont être perdus.
C’est exactement ce qu’il se passe dans l’exemple. Lors de la mise au même exposant, le significande de va être divisé par 257, ce qui vide entièrement les 52 bits du significande, et il ne reste plus rien à additionner !
Annulation catastrophique
L’annulation catastrophique est le nom donné à la perte de précision qui se produit lors de la soustraction de deux flottants très proches. En effet, quand on soustrait deux flottants très proches, il est possible de perdre de nombreux chiffres utiles, alors même que le résultat théorique peut être stocké dans un flottant.
Regardons ce phénomène sur un exemple : la soustraction de et . Le résultat de ce calcul est évidemment , mais la machine fait une erreur grossière :
>>> import math
>>> M = math.sqrt(2) * (1 + 10**-14)
>>> m = math.sqrt(2)
>>> M - m
1.42108547152020037e-14
La troisième décimale est déjà fausse puisque le résultat correctement arrondi est , qu’il est tout fait possible de stocker dans un flottant.
Les flottants utilisés par Python ici sont binaires, mais le phénomène est similaire en décimal et plus facile à comprendre. Si l’on stockait exactement 16 chiffres décimaux pour faire ce calcul, voici ce qu’il se passerait :
La troisième décimale est fausse ici aussi. On voit dans ce calcul que la plupart des chiffres sont identiques et s’annulent en masse. En fin de compte, ils n’apportent rien au calcul. On se retrouve donc avec seulement quelques chiffres utiles et très peu de précision ! C’est là l’essence du phénomène d’annulation catastrophique.
Pour un autre exemple moins artificiel et plus développé, je vous invite à lire cet article, qui traite d’un phénomène d’annulation catastrophique dans le calcul des racines de trinômes du second degré.
Les phénomènes d’arrondi, d’absorption et d’annulation catastrophique sont inhérents aux opérations avec les flottants et ne peuvent être évités que par des calculs astucieux, quand cela est possible, ou en utilisant des nombres ayant une plus grande précision, ce qui se fait souvent au détriment de la performance.
- Il s’agit du calcul direct, sans arrondi intermédiaire, de l’opération . C’est une opération très utilisée en traitement du signal, et qui est souvent optimisée dans les processeurs.↩
Enchaînements d'opérations
Combinaison de plusieurs calculs
La norme définit précisément le comportement pour une unique opération, mais laisse une certaine liberté aux langages quant au comportement pour une combinaison d’opérations. Les règles exactes diffèrent donc d’un langage à l’autre, mais les règles générales sont tout de même conservées. On traite d’abord :
- les calculs entre parenthèses,
- puis les multiplications et divisions,
- enfin les additions et soustractions.
Quand plusieurs calculs de priorités identiques s’enchaînent, ils sont généralement effectués dans l’ordre, de gauche à droite. En somme, les priorités sont tout à fait identiques à celles avec les réels.
Le point le plus subtil concerne les arrondis intermédiaires. En effet, certains langages ou processeurs sont capables d’enchaîner les calculs en utilisant une précision étendue (80 bits au lieu de 64, par exemple). Dans ce cas-là, les résultats intermédiaires ne sont pas arrondis comme un résultat final, mais avec plus de décimales. Les calculs s’enchaînent ensuite avec ces opérandes en précision étendue, avant un arrondi final lors de l’affectation. Un calcul dont les résultats intermédiaires seraient affectés à des variables peut alors ne pas donner le même résultat qu’un calcul effectué tout d’un coup !
En pratique, cela a assez peu d’influence, mais si vous souhaitez avoir des détails, référez-vous au manuel de votre langage préféré.
Cette liberté laissée au langage par la norme mène à des problèmes de reproductibilité des résultats. Par exemple, une même simulation effectuée sur deux machines différentes peut donner des résultats différents ; qui croire dans des cas comme ça ?
Pour les calculs dont la reproductibilité compte, par exemple pour valider le résultat d’une simulation, la norme donne carrément une méthode pour y parvenir ! Elle consiste principalement à éviter soigneusement toute une série d’opérations dont les résultats diffèrent d’une machine conforme à l’autre.
Les calculs avec les flottants ressemblent de loin à ceux avec les réels. Pourtant une grande partie des propriétés des réels sont absentes. En particulier, l’arithmétique flottante :
- présente des phénomènes d’absorption, où un opérande est « mangé » par un autre ;
- est non distributive, autrement dit, factoriser ou développer affecte généralement le résultat ;
- est non associative, c’est-à-dire que l’ordre des calculs importe.
Quelques propriétés de l’arithmétique flottante
Commutativité
Puisque quand on effectue une opération sur des flottants, le résultat est l’arrondi correct du résultat exact, alors l’arithmétique sur les flottants est commutative : l’ordre des termes dans une addition ou une multiplication ne change pas le résultat.
Que l’on effectue ou , il se passera exactement la même chose, à savoir l’arrondi des opérandes, le calcul de l’addition et l’arrondi correct du résultat.
On retrouve là une propriété des réels, ce qui est plutôt agréable, car d’autres propriétés des réels ne sont pas applicables aux flottants.
Non associativité
Les opérations dans les réels sont associatives. Par exemple, effectuer les opérations ou donne un résultat identique quand on travaille avec des réels.
Dans les flottants, cela ne marche pas dans le cas général. En effet, l’ordre des opérations pour est le suivant :
- arrondi des opérandes et ,
- calcul de + avec les opérandes arrondis,
- arrondi du résultat + ,
- calcul de l’arrondi de ,
- addition du résultat arrondi de avec ,
- arrondi du résultat final.
Les différentes opérations d’arrondi peuvent emmener le résultat dans une direction différente en fonction de l’ordre dans lequel les opérations sont effectuées, et on perd alors l’associativité dont disposent les réels.
Ce phénomène est assez simple à voir en cas de dépassement. Par exemple, si l’opération provoque un dépassement, c’est-à-dire un résultat infini, alors l’addition de conservera cet infini. Pourtant, il existe des cas où l’addition de d’abord et ensuite de ne provoque pas de dépassement. C’est le cas par exemple quand est très positif, mais que est très négatif.
Voyons la non-associativité sur un exemple :
>>> a = 9e307
>>> b = 9e307
>>> c = -2e306
>>> (a + b) + c # dépassement
inf
>>> a + (b + c) # pas de dépassement
1.78000000000000023e+308
Non distributivité
Dans les réels, l’addition est distributive sur la multiplication. On peut écrire la chose suivante :
Dans les flottants, cela n’est plus vrai, encore une fois à cause des erreurs d’arrondis. Il n’y a pas de raison que les arrondis soient toujours exacts avec les deux opérations, et on perd alors la distributivité.
Ce phénomène arrive par exemple en cas de dépassement de la somme . Le calcul effectué en développant évite alors le dépassement, pour peu que soit relativement petit, et on obtient un autre résultat. Ce phénomène existe aussi avec des nombres normaux, notamment si dans une des deux formes, l’addition provoque une annulation catastrophique.
Voyons la non-distributivité sur un exemple :
>>> a = 1e-10
>>> b = 9e307
>>> c = 9e307
>>> a * (b + c) # on obtient l'infini
inf
>>> a * b + a * c # on obtient un autre résultat et on évite l'infini
1.80000000000000021e+298
Exemples de situations problématiques
Accumulation d’erreurs
Lorsqu’on effectue des additions, ou des multiplications, les unes à la suite des autres, les erreurs s’accumulent, de sorte qu’après un nombre important d’opérations, la précision obtenue n’est pas au niveau attendu d’un calcul avec des flottants, c’est-à-dire de l’ordre de 10-15.
Prenons l’exemple, assez artificiel suivant : sommer fois la valeur dans le but d’obtenir le résultat . En prenant de plus en plus grand, et donc de plus en plus petit, on fera des calculs de plus en plus longs pour aboutir au même résultat.
Le programme ci-dessous montre comment on effectue le calcul pour .
>>> v = 0.
for i in range(10):
v = v + .1
1-v
1.1102230246251565404236316680908203125e-16
En effectuant ce calcul pour différentes valeurs de , on obtient le résultat du tableau ci-dessous.
| Additions | Incrément | Écart à 1 |
|---|---|---|
On voit que plus le nombre d’opérations est important, moins la précision obtenue est élevée. À partir de quelques dizaines de milliers d’opérations, on commence à perdre plusieurs chiffres significatifs, et à partir d’un million d’opérations, on commence à disposer que d’un tiers de la précision disponible !
Les exemples de la vie réelle ne sont pas forcément aussi désavantageux que celui-ci, mais ce phénomène arrive nécessairement et est difficile à contrôler dans les calculs longs, comme les simulations physiques utilisant un pas de temps très court. Il s’agit d’ailleurs d’un phénomène limitant la précision temporelle des méthodes de simulation les plus simples, comme la méthode d’Euler.
Perte massive de chiffres significatifs
Pour effectuer un calcul, il y a parfois plusieurs formes possibles, qui sont équivalentes lorsqu’on travaille avec les réels. Par exemple, pour évaluer un polynôme, il est possible de travailler à partir de la forme factorisée ou de la forme développée, sans changer le résultat.
Avec les flottants, le choix de la forme du calcul peut influer de manière importante sur le résultat. En effet, en fonction des valeurs prises par les variables, la propagation des erreurs d’arrondi ne se fait pas de la même manière, donc il est possible de perdre grandement en précision avec les opérations dans un ordre désavantageux.
Prenons l’exemple du calcul de la fonction polynomiale suivante :
Deux formes s’offrent à nous : la forme factorisée et la forme développée .1 Voyons ce qu’il se passe quand on calcule la fonction pour des valeurs de proches de 2 avec la figure suivante.
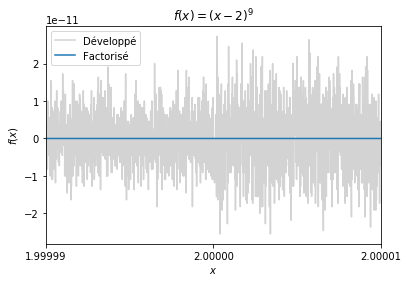
On voit immédiatement que la forme factorisée est plus précise. En fait, la forme développée présente une l’alternance du signe des termes, ce qui fait qu’en pratique, on effectue des soustractions entre des termes d’ordres de grandeur similaires, et on a alors un phénomène d’annulation massive.
Convergence de la série harmonique
Dans le monde des flottants, on ne peut pas calculer la série harmonique n’importe comment. La série harmonique désigne la somme suivante :
Dans le monde des réels, cette somme diverge quand n tend vers l’infini, et évidemment, pour n fixé, l’ordre de sommation n’a pas d’importance. Cependant, avec les nombres flottants, quelques précautions sont à prendre. Regardez le tableau ci-dessous, qui montre les différences obtenues en faisant croître n ou en le faisant décroître.
| Croissant | Décroissant | |
|---|---|---|
| 105 | 12,090146129863335 | 12,090146129863408 |
| 107 | 16,695311365857272 | 16,695311365859965 |
| 108 | 18,997896413852555 | 18,997896413853447 |
Le problème n’est pas seulement lié à l’ordre de sommation, car dans les flottants, la série harmonique converge ! En effet, pour suffisamment grand, est extrêmement petit, et un phénomène de soupassement provoque un arrondi vers zéro. Il y a ainsi un nombre fini de termes non-nuls et la série converge. Il faut cependant atteindre des nombres de l’ordre de en double précision.
Récurrence de Müller et Kahan
Avec les flottants, un calcul de suite tout simple peut présenter quelques surprises. Voici une petite récurrence proposée par Kahan et Muller, écrite ici en Python :
x0 = 11./2.
x1 = 61./11.
for i in range(100):
x2 = 111. - (1130. - 3000./x0) / x1
x0 = x1
x1 = x2
print(x2)
Cet algorithme est assez amusant. En effet, en calculant la limite mathématiquement, avec des réels, on converge vers 6. Cependant, lors de l’exécution de ce programme avec des doubles, on converge vers 100.
Ce qu’il se passe, c’est qu’en calculant 11/2 et 61/11, une petite erreur d’arrondi se glisse dans le résultat. Là où cette récurrence est subtile, c’est que cette erreur est commune à tous les types flottants binaires, et donc qu’augmenter la précision ne la résout pas. Une fois cette erreur faite, le changement des valeurs initiales suffit à transformer la suite, qui converge vers une autre valeur que celle attendue (à savoir 100 au lieu de 6).
Le tableau ci-dessous montre la différence entre le calcul correct de la suite et celui effectué par le programme vu ci-avant.
| Calcul avec des flottants | Calcul avec des réels |
|---|---|
| 5,5901… | 5,5901… |
| 5,6334… | 5,6334… |
| 5,6746… | 5,6746… |
| 5,7133… | 5,7133… |
| 5,7491… | 5,7491… |
| 5,7818… | 5,7818… |
| 5,8113… | 5,8113… |
| 5,8376… | 5,8376… |
| 5,8610… | 5,8609… |
| 5,8835… | 5,8813… |
| 5,9359… | 5,8991… |
| 6,5344… | 5,9145… |
| 15,4130… | 5,9277… |
| 67,4723… | 5,9390… |
| 97,1371… | 5,9486… |
| 99,8246… | 5,9568… |
| 99,9895… | 5,9637… |
| 99,9993… | 5,9696… |
| 99,9999… | 5,9745… |
| 99,9999… | 5,9787… |
| 99,9999… | 5,9822… |
| 99,9999… | 5,9851… |
| 99,9999… | 5,9875… |
| 99,9999… | 5,9896… |
- On passe de la forme factorisée à la forme développée à l’aide de la formule du binôme de Newton.↩
Exemple d'algorithme intelligent : la sommation compensée de Kahan
L’exemple de la série harmonique montre que pour les flottants, l’ordre de la sommation compte, parce qu’on risque de perdre des petits morceaux en cours de route par absorption ou par annulation massive. La sommation compensée de Kahan est un algorithme qui résout astucieusement ce problème.
L’idée générale de l’algorithme est de ramasser les miettes (les bits de poids faible) qui seraient absorbées par la somme et de les ajouter aux éléments (plus petits) avant d’ajouter le tout à la somme courante (plus grande), ce qui limite l’absorption.
Le morceau de code ci-dessous implémente cet algorithme.
def sum_kahan(list):
s = 0 # accumulateur pour la somme
c = 0 # compensation pour les bits de poids faible
for e in list:
y = e - c # l'élément à sommer corrigé par la compensation des bits de poids faible
t = s + y # on perd des bits de poids faible avec cette addition
c = (t - s) - y # cœur de l'algo : récupération des bits de poids faible (cas extrême : si y est entièrement absorbé, il est inclus dans c pour être ajouté à l'élément suivant de la liste)
s = t # on passe à l'étape suivante
print("s =", s, "| c =", c) # affichage pour la démonstration
return s
L’intérêt de cet algorithme est essentiellement de sommer de très longues listes sans perdre trop de précision, mais on peut le voir fonctionner sur un exemple. On y somme une liste contenant un nombre relativement grand et des miettes.
>>> eps = 10**-17
>>> l = [1, eps, eps, eps, eps, eps, eps, eps, eps, eps, eps, eps, eps, eps, eps, eps]
>>> sum_kahan(l)
1.0000000000000002
Le résultat 1.0000000000000002 est ce qu’on obtiendrait en arrondissant le résultat exact de la somme vers les flottants. On peut le comparer avec le résultat de l’algorithme naïf qui donne :
>>> sum(l)
1.0
Ici, la somme n’a pas ramassé les miettes et on a seulement le premier élément de la liste.
En regardant l’affichage, on peut comprendre comment l’algorithme de Kahan opère pour arriver à faire mieux que l’algorithme naïf :
s = 1 | c = 0 # somme du premier élément, tout va bien
s = 1.0 | c = -1e-17 # l'élément est absorbé dans la somme, il est retenu dans la compensation
s = 1.0 | c = -2e-17 # idem
s = 1.0 | c = -3e-17 # idem
s = 1.0 | c = -4e-17 # idem
s = 1.0 | c = -5.0000000000000005e-17 # idem
s = 1.0 | c = -6e-17 # idem
s = 1.0 | c = -7e-17 # idem
s = 1.0 | c = -8e-17 # idem
s = 1.0 | c = -9.000000000000001e-17 # idem
s = 1.0 | c = -1.0000000000000001e-16 # idem
s = 1.0 | c = -1.1000000000000001e-16 # idem
s = 1.0000000000000002 | c = 1.020446049250313e-16 # une partie de la compensation a pu être sommée ! La compensation accumulée diminue légèrement.
s = 1.0000000000000002 | c = 9.20446049250313e-17 # idem
s = 1.0000000000000002 | c = 8.20446049250313e-17 # idem
s = 1.0000000000000002 | c = 7.20446049250313e-17 # idem
s = 1.0000000000000002 | c = 6.20446049250313e-17 # idem
s = 1.0000000000000002 | c = 5.2044604925031294e-17 # idem
s = 1.0000000000000002 | c = 4.204460492503129e-17 # idem
Une variante de cet algorithme, la sommation de Neumaier, est utilisée par le langage Python pour sa fonction sum() depuis la version 3.12 ! Cela permet aux utilisateurs de bénéficier d’une meilleure précision sans expertise spécifique et l’impact en performance est minime. Pour une précision encore meilleure, la fonction math.fsum() utilise un algorithme plus évolué encore, mais la performance en est affectée.