Fonctions de fonctions - Introduction aux fonctions • Bibliothèque • Zeste de Savoir

Dans ce chapitre, nous passons au niveau supérieur puisque nous allons maintenant transformer… des fonctions ! Cela peut paraître surprenant et un peu artificiel au premier abord, mais les différentes techniques de transformations des fonctions sont redoutablement utiles en maths et en sciences d’une manière générale.

Image utilisateur

Ne soyez pas effrayés, nous allons aborder les choses en douceur.

Fonctions branchées
Opérations de fonctions
Cumuls et variations

Fonctions branchées

Fonctions à la chaîne

L’une des façons les plus élémentaires de transformer des fonctions est d’en prendre plusieurs et de faire des branchements entre leurs entrées et leur sorties.

Prenons deux fonctions et branchons la sortie de la première à l’entrée de la seconde :

Image utilisateur

Nous obtenons ainsi une nouvelle fonction qu’on appelle la composée de la fonction 1 et de la fonction 2. En notation algébrique, si on note $f$ et $g$ ces deux fonctions, alors la composée de $f$ et $g$ se note $g\circ f$ et se lit «  $g$ rond $f$  » ou «  $f$ suivie de $g$  ». Ainsi, on a :

$g\circ f(x)=g(f(x)).$

Autrement dit, on calcule d’abord $f(x)$ , avant de le mettre dans la fonction $g$ .

Le petit rond désigne l’opération de composition des fonctions, de la même façon que les symboles + ou × désigne des opérations sur les nombres.

Prenons un exemple pour être sûr de bien comprendre. Supposons que $f$ multiplie les nombres par 2 et que $g$ ajoute le nombre 3, on a donc :

$f(x)=2x ~~~\text{et}~~~ g(x)=x+3.$

Alors la composée de $f$ et de $g$ est une fonction qui prend un nombre, le multiplie par 2 et lui ajoute 3 d’un seul coup.

$g\circ f(x)=2x+3.$

Par exemple, si on met 5 dans notre nouvelle machine, il en ressortira directement le nombre 13.

Méfiez-vous car le résultat d’une composition dépend de l’ordre dans lequel on compose : la fonction $g\circ f$ est celle qui effectue d’abord la fonction $f$ et ensuite la fonction $g$ . Si dans l’exemple précédent on fait la composition dans l’autre sens, on trouve : $f\circ g(x)=(x+3)\times 2=2x+6.$ C’est une source très fréquente d’erreurs pour les débutants.

Les ensembles doivent se suivre

Jusque-là, nous avons oublié un détail dans notre description des fonctions composées : les ensembles de départ et d’arrivée. Il faut évidemment y faire très attention car si notre fonction 1 renvoie des figures géométriques et que notre fonction 2 est une suite qui ne prend que des nombres entiers en entrée, alors forcément ça va beaucoup moins bien marcher.

L’idéal, c’est que l’ensemble de départ de la deuxième fonction soit égal à l’ensemble d’arrivée de la première. Comme ça pas de problème, tout s’enchaîne naturellement. Si $f$ et $g$ sont définies de la sorte :

\begin{aligned} f \colon E &\to F\\ x &\mapsto f(x) \end{aligned} ~~~\text{et}~~~ \begin{aligned} g \colon F &\to G\\ x &\mapsto g(x) \end{aligned}

alors leur composée se définit comme ceci :

\begin{aligned} g \circ f \colon E &\to G\\ x &\mapsto g(f(x)). \end{aligned}

Pour être un peu plus large, vous pouvez remarquer qu’il est possible de se contenter de l’inclusion de l’ensemble d’arrivée de $f$ dans l’ensemble de départ de $g$ pour que ça marche.

À trois, à quatre, ou plus si affinité…

Nous venons de voir comment composer deux fonctions, mais il est bien entendu possible d’en enfiler autant que l’on veut les unes à la suite des autres. Si on dispose de trois fonctions $f$ , $g$ et $h$ dont les ensembles de départ et d’arrivée s’enchaînent comme il faut, alors il est possible de construire la fonction $h\circ g\circ f$ qui effectue d’abord $f$ , puis $g$ , puis $h$  :

$h\circ g\circ f(x)=h(g(f(x))).$

Et si on dispose d’une fonction dont l’ensemble de départ est égal à l’ensemble d’arrivée, il est possible de la composer avec elle même ! Cela se note alors sous la forme d’une puissance :

\begin{aligned} f^2 &= f \circ f\\ f^3 &= f \circ f \circ f\\ f^4 &= f \circ f \circ f \circ f \end{aligned}

et ainsi de suite, une fois que vous avez compris le principe, vous pouvez brancher autant de fonctions que vous voulez dans l’ordre que vous voulez.

Opérations de fonctions

Les entrées et les sorties s’emmêlent

Pour l’instant, nous avons uniquement composé des fonctions à la chaîne, mais les choses peuvent commencer à devenir vraiment tordues, si on se met à utiliser des fonctions ayant plusieurs entrées ou plusieurs sorties.

Si par exemple on a d’une part deux fonctions avec une entrée et une sortie chacune, et d’autre part une fonction à deux entrées, alors il est possible de les assembler de la façon suivante :

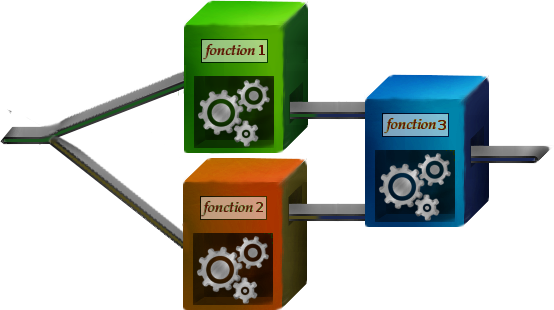
Image utilisateur

En clair cette fonction marche de la façon suivante :

on met notre objet d’entrée à la fois dans la fonction 1 et la fonction 2 :
on récupère les deux résultats obtenus et on en met un dans chaque entrée de la fonction 3 ;
on récupère le résultat à la sortie de la fonction 3.

Si par exemple la fonction 1 double les nombres ( $x\mapsto=2x$ ), que la fonction 2 les met au carré ( $x\mapsto=x^2$ ) et que la fonction 3 est simplement l’addition ( $(x,y)\mapsto=x+y$ ), alors tout ce montage donne simplement une fonction qui a un nombre associe la somme de son double et de son carré : $x\mapsto 2x+x^2$ .

Faire des opérations de fonctions

Ce genre de construction permet surtout de faire des opérations de fonctions.

Prenons par exemple le cas de l’addition de deux fonctions dont nous venons de voir un exemple. Si on dispose de deux fonctions numériques $f$ et $g$ , leur somme $f+g$ est alors la fonction qui additionne les résultats donnés par $f$ et par $g$ . Elle est donc définie de la façon suivante :

\begin{aligned} f + g \colon \mathbb{R} &\to \mathbb{R}\\ x &\mapsto f(x) + g(x) \end{aligned}

Autrement dit, on a $(f+g)(x)=f(x)+g(x)$ .

Et de la même façon, on peut définir $f-g$ , $f\times g$ , $f\div g$ ou toute autre opération possible et imaginable, pourvu que cette opération soit possible dans l’ensemble d’arrivée des fonctions.

\begin{aligned} f - g \colon \mathbb{R} &\to \mathbb{R}\\ x &\mapsto f(x) - g(x) \end{aligned} \qquad \begin{aligned} f \times g \colon \mathbb{R} &\to \mathbb{R}\\ x &\mapsto f(x) \times g(x) \end{aligned} \qquad \begin{aligned} f \div g \colon \mathbb{R} &\to \mathbb{R}\\ x &\mapsto f(x) \div g(x) \end{aligned}

On peut également faire ce genre de chose avec des fonctions géométriques. Par exemple, l’intersection de deux figures est formée par les points qui appartiennent aux deux à la fois. Ainsi, on peut imaginer l’intersection de deux fonctions géométriques qui rend l’intersection de leur deux sorties.

Si ce genre de construction vous semble encore très obscur, ne vous en faites pas, ça va venir. En maths, il faut souvent du temps pour apprivoiser les concepts, il ne s’agit là que d’une première approche et tout ceci s’éclairera au fur et à mesure que vous avancerez dans l’étude des fonctions.

Cumuls et variations

Nous allons finir ce chapitre avec une brève introduction aux calculs de cumuls et de variations des fonctions numériques. Cette branche de l’analyse que nous n’allons qu’effleurer est en réalité l’une des plus importantes qui soit et se trouve au cœur même de l’étude des fonctions numériques.

La somme et la différence

Prenons tout de suite un exemple. Considérons une suite $(u_n)$ qui représente le nombre de caramels mous produits mondialement chaque année. Par exemple, si $u_{2000}=100\,000\,000$ , cela signifie que cent millions de caramels mous ont été produits en l’an 2000.

Il est possible à partir de cette suite de vouloir en tirer d’autres informations. On peut par exemple vouloir savoir combien de caramels mous ont été produits sur une période plus vaste, dans ce cas, on va devoir sommer les termes de la suite. Par exemple, le nombre total de caramels mous produits au XXe siècle est égal à

u_{1901}+u_{1902}+u_{1903}+\cdots+u_{1999}+u_{2000}=\sum_{n=1901}^{2000}u_n.

Le symbole $\Sigma$ (sigma) est utilisé en mathématiques pour faire des sommes. Si vous ne savez pas l’utiliser vous pouvez vous reporter au chapitre du cours sur les opérations qui lui est consacré (bientôt sur Zds).

On peut aussi ne pas être intéressés par la quantité précise de caramels produits, mais plutôt par leur évolution : la production est-elle plutôt en diminution ou en augmentation ? Dans ce cas, les nombres qui nous intéressent sont les différences de production d’une année à l’autre :

\Delta u_n=u_{n}-u_{n-1}

Ainsi, si cent millions de caramels mous ont été produits en 2000 contre seulement quatre-vingt-dix-sept millions en 1999, alors on a $\Delta u_{2000}=3\,000\,000$ .

La lettre grecque $\Delta$ (delta) est utilisée en mathématiques pour noter une différence.

Vous pouvez constater que les transformations $\Sigma$ et $\Delta$ peuvent alors être considérées comme des fonctions qui prennent une suite en entrée.

En réalité, ces deux transformations sont les deux principaux outils qui permettent d’étudier les variations de la suite. Des transformations équivalentes existent pour les fonctions continues et se nomment la dérivée et l’intégrale. Nous verrons toutes ces transformations plus en détail dans les cours consacrés aux suites et aux fonctions réelles.