La programmation modulaire I : les packages

• Les chaînes de caractères
• Sommaire
• Les fichiers

Pour ce nouveau chapitre, nous allons revenir sur les tableaux.

Rassurez-vous, les tableaux ne constitueront qu'un prétexte et non pas le coeur de ce chapitre. Nous avons vu tout ce qu'il y avait à voir sur les tableaux. Mais cela ne doit pas nous faire oublier leur existence, bien au contraire. Nous allons très régulièrement les utiliser. Mais, si vous avez effectué les exercices sur les tableaux, vous avez du vous rendre compte qu'il fallait très régulièrement réécrire les mêmes fonctions, les mêmes procédures, les mêmes déclarations de type… Se pose alors la question :

Et la réponse, vous vous en doutez, est oui ! Ces fichiers, ce sont les fameux packages !

• Les fichiers nécessaires
• Notre première procédure… empaquetée
• Variables et constantes globales
• Trouver et classer les fichiers
• Compléter notre package (exercices)
• Vecteurs et calcul vectoriel (optionnel)

Les fichiers nécessaires

Avant de créer notre premier package, nous allons créer un nouveau programme appelé Test. dans lequel nous allons pouvoir tester toutes les procédures, fonctions, types, variables que nous allons créer dans notre package. Voici la structure initiale de ce programme :

1
2
3
4
5
6
7
8

with Integer_Array ; 
use Integer_Array ; 

procedure Test is
   T : T_Vecteur ; 
begin

end Test ;

Ce package integer_array, c'est justement le package que nous allons créer et le type T_Vecteur est un « ARRAY OF Integer » de longueur 10 (pour l'instant). Pour l'instant, si l'on tente de compiler ce programme, nous nous trouvons face à deux obstacles :

• Il n'y a aucune instruction entre BEGIN et END !
• Le package Integer_Array est introuvable (tout simplement parce qu'il est inexistant)

Nous allons donc devoir créer ce package. Comment faire ? Vous allez voir, c'est très simple : cliquez sur File > New deux fois pour obtenir deux nouvelles feuilles vierges.

Non, non ! J'ai bien dit deux fois ! Vous comprendrez pourquoi ensuite. Sur l'une des feuilles, nous allons écrire le code suivant :

1
2
3
4
5
6

WITH Ada.Integer_Text_IO, Ada.Text_IO ;
USE Ada.Integer_Text_IO, Ada.Text_IO ;

PACKAGE BODY Integer_Array IS

END Integer_Array ;

Puis, dans le même répertoire que votre fichier Test.adb, enregistrer ce nouveau fichier sous le nom Integer_Array.adb.

Dans le second fichier vierge, écrivez :

1
2
3

PACKAGE Integer_Array IS

END Integer_Array ;

Enfin, toujours dans le même répertoire, enregistrer ce fichier sous le nom Integer_Array.ads. Et voilà ! Vous venez de créer votre premier package ! Bon, j'admets qu'il est un peu vide, mais nous allons remédier à ce défaut.

Notre première procédure… empaquetée

Vous remarquerez que cela ressemble un peu à ce que l'on a l'habitude d'écrire, sauf qu'au lieu de créer une procédure, on crée un package.

Nous y arrivons. Pour comprendre, nous allons créer une procédure qui affiche un tableau. Vous vous souvenez ? Nous en avons déjà écrit plusieurs (souvent appelées Afficher). Moi, je décide que je vais l'appeler Put() comme c'est d'usage en Ada.

Encore une fois, rassurez-vous et faites moi confiance, tout va bien se passer et je vous expliquerai tout ça à la fin («Oui, ça fait beaucoup de choses inexpliquées», dixit Mulder & Scully ). Dans le fichier Test.adb, nous allons écrire:

1
2
3
4
5
6
7
8
9

WITH Integer_Array ; 
USE Integer_Array ; 

PROCEDURE Test IS
   T : T_Vecteur(1..10) ; 
BEGIN
   T := (others => 0) ; 
   Put(T,2) ; 
END Test ;

Je voudrais, en effet, que notre procédure Put() puisse également gérer le nombre de chiffres affichés, si besoin est. Puis, dans le fichier Integer_Array.ads, nous allons ajouter ces lignes entre IS et END :

1
2

TYPE T_Vecteur IS ARRAY(integer range <>) OF Integer ;
PROCEDURE Put (T : IN T_Vecteur; Fore : IN Integer := 11);

Je prends les devants : il n'y a aucune erreur, j'ai bien écrit un point-virgule à la fin de la procédure et pas le mot IS. Pourquoi ? Pour la simple et bonne raison que notre fichier Integer_Array.ads n'est pas fait pour contenir des milliers de lignes de codes et d'instructions ! Il ne contient qu'une liste de tout ce qui existe dans notre package. On dit que la ligne « PROCEDURE Put (T : IN T_Vecteur; Fore : IN Integer := 11); » est la spécification (ou le prototype) de la procédure Put(). La spécification de notre procédure ne contient pas les instructions nécessaires à son fonctionnement, il indique seulement au compilateur : «voilà, j'ai une procédure qui s'appelle Put() et qui a besoin de ces 2 paramètres !».

Le contenu de notre procédure (ce que l'on appelle le corps ou BODY en Ada), nous allons l'écrire dans notre fichier Integer_Array.adb, entre IS et END. Vous pouvez soit reprendre l'une de vos procédures d'affichage déjà créées et la modifier, soit recopier la procédure ci-dessous :

1
2
3
4
5
6
7

PROCEDURE Put(T : IN T_Vecteur ; Fore : IN Integer := 11) IS
BEGIN
   FOR I IN T'RANGE LOOP
      Put(T(I),Fore) ;
      put(" ; ") ;
   END LOOP ;
END Put ;

Enregistrer vos fichiers, compiler votre programme Test.adb et lancez-le : vous obtenez une jolie suite de 0 séparés par des points virgules. Cela nous fait donc un total de trois fichiers, dont voici les codes :

• Test.adb :

1
2
3
4
5
6
7
8
9

WITH Integer_Array ; 
USE Integer_Array ; 

PROCEDURE Test IS
   T : T_Vecteur(1..10) ; 
BEGIN
   T := (others => 0) ; 
   Put(T,2) ; 
END Test ;

• Integer_Array.ads :

1
2
3
4

PACKAGE Integer_Array IS
   TYPE T_Vecteur IS ARRAY(Integer range <>) OF Integer ;
   PROCEDURE Put (T : IN T_Vecteur; Fore : IN Integer := 11);
END Integer_Array ;

• Integer_Array.adb :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

WITH Ada.Integer_Text_IO, Ada.Text_IO ;
USE Ada.Integer_Text_IO, Ada.Text_IO ;

PACKAGE BODY Integer_Array IS
   PROCEDURE Put(T : IN T_Vecteur ; Fore : IN Integer := 11) IS
   BEGIN
      FOR I IN T'RANGE LOOP
         Put(T(I),Fore) ;
         put(" ; ") ;
      END LOOP ;
   END Put ;
END Integer_Array ;

Nous pourrions résumer la situation par ce schéma :

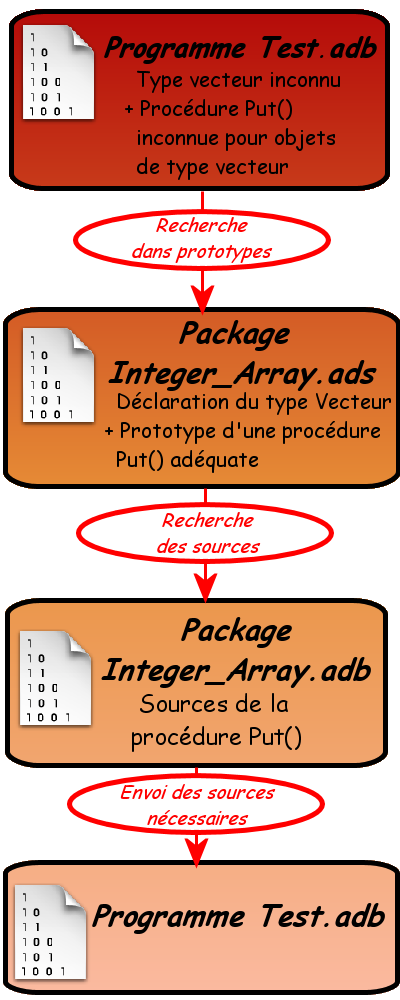
Reste l'histoire de la procédure Put(). La procédure Put() ne constitue pas un mot réservé du langage, pour l'utiliser vous êtes obligés de faire appel à un package :

• Integer_Text_IO pour afficher un Integer ;
• Float_text_IO pour afficher un float ;
• notre package Integer_Array pour afficher un T_Vecteur.

À chaque fois, c'est une procédure Put() différente qui apparaît et ce qui les différencie pour le compilateur, ce sont le nombre et le type des paramètres de ces procédures. Pour cela, GNAT s'appuie sur les spécifications qu'il trouve dans les fichiers ads. En cas d'hésitation, le compilateur vous demandera de spécifier de quelle procédure vous parlez en écrivant :

• Integer_Text_IO.Put() ou
• Float_text_IO.Put() ou
• Integer_Array.Put().

Variables et constantes globales

Je vous ai plusieurs fois dit qu'une variable ne pouvait exister en dehors de la procédure, de la fonction ou du bloc de déclaration où elle a été créée. Ainsi, s'il est impossible que deux variables portent le même nom dans un même bloc, il est toutefois possible que deux variables aient le même nom si elles sont déclarées dans des blocs distincts (par bloc, j'entends procédure, fonction ou bloc DECLARE). De même, je vous ai également expliqué que le seul moyen pour qu'un sous-programme et le programme principal puissent se transmettre des valeurs, c'est en utilisant les paramètres. Eh bien tout cela est faux.

Il ne s'agit pas d'un mensonge mais d'une imprécision. Tout ce que je vous ai dit est à la fois le cas général et la méthode qu'il est bon d'appliquer pour générer un code de qualité. Toutefois, il est possible de créer des variables qui outrepassent ces restrictions. Ce sont ce que l'on appelle les variables globales. Il s'agit de variables ou constantes déclarées dans un package. Dès lors, tout programme utilisant ce package y aura accès : elles seront créées au démarrage du programme et ne seront détruites qu'à sa toute fin. De plus, un sous-programme pourra y faire appel sans qu'elle ne soit citée dans les paramètres.

Vous vous demandez sûrement pourquoi nous n'avons pas commencé par là ? Vous devez savoir qu'utiliser des variables globales est très risqué et que c'est une pratique à proscrire autant que possible. Imaginons une fonction itérative (utilisant une boucle) qui modifierait notre variable dans le but de calculer son résultat. La fonction se termine, transmet son résultat et libère la mémoire qu'elle avait réquisitionnée : ses variables internes sont alors supprimées… mais pas la variable globale qui continue d'exister. Sauf que sa valeur a été modifiée par la fonction, et la disparition de cette dernière ne réinitialisera pas la variable globale. Qui sait alors combien d'itérations ont été effectuées ? Comment retrouver la valeur initiale pour rétablir un fonctionnement normal du programme ?

L'usage des variables globales doit donc être limité aux cas d'absolue nécessité. Si par exemple, une entreprise dispose d'un parc d'imprimantes en réseaux, quelques variables globales enregistrant le nombre total d'imprimantes ou le nombre d'imprimantes libres seront nécessaires. Et encore, le nombre d'imprimantes libres peut être modifié par plusieurs programmes successivement ou simultanément ! Cela créera de nombreux problèmes que nous découvrirons quand nous aborderons le multitasking.

L'usage le plus fréquent (et que je vous autorise volontiers) est celui des constantes globales. Celles-ci peuvent vous permettre d'enregistrer des valeurs que vous ne souhaiter pas réécrire à chaque fois afin d'éviter toute erreur. Il peut s'agir par exemple du titre de votre jeu, des dimensions de la fenêtre de votre programme ou de nombres spécifiques comme dans l'exemple ci-dessous :

1
2
3
4
5
6

PACKAGE P_Constantes IS
   Pi       : Constant Float := 3.14159 ;             --Le célèbre nombre Pi
   Exp      : Constant Float := 2.71828 ;             --La constante de Neper
   Phi      : Constant Float := 1.61803 ;             --Le nombre d'or
   Avogadro : Constant Float := 6,022141 * 10.0**23 ; --La constante d'Avogadro
END P_Constantes ;

Et voilà quelques fonctions utilisant ces constantes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

WITH P_Constantes ;       USE P_Constantes ;
   ...
FUNCTION Perimetre(R : Float) RETURN Float IS
BEGIN
   RETURN 2.0 * Pi * R ; 
END Perimetre ; 

FUNCTION Exponentielle(x : Float) RETURN Float IS
BEGIN
   RETURN Exp ** x ; 
END Exponentielle ;
   ...

Vous remarquerez que Pi ou Exp n'ont jamais été déclarées dans mes fonctions ni même passées en paramètre. Elles jouent ici pleinement leur rôle de constante globale : il serait idiot de calculer le périmètre d'un cercle avec autre chose que le nombre $\pi$ !

C'est dans ce cas, complètement inutile : mon package ne comporte que des constantes. Je n'ai pas de corps à détailler. Les fichiers adb (Ada Body), ne sont utiles que s'il faut décrire des procédures ou des fonctions. Si le package ne comporte que des types ou variables globales, le fichier ads (Ada Specifications) suffit. Rappelez-vous le schéma de tout à l'heure : les programmes cherchent d'abord les spécifications dans le fichier ads !

Trouver et classer les fichiers

Les packages fournis avec GNAT

Où se trouvent les packages Ada ?

En effet. Tous les packages que nous citons en en-tête depuis le début de ce cours ont des fichiers correspondants : un fichier ads et éventuellement un fichier adb. Pour découvrir des fonctionnalités supplémentaires de Ada.Text_IO, Ada.Numerics.Discrete_Random ou Ada.Strings.Unbounded, il suffit simplement de trouver ces fichiers ads et des les examiner. Il est inutile d'ouvrir le corps des packages, en général peu importe la façon dont une procédure a été codée, ce qui compte c'est ce qu'elle fait. Il suffit donc d'ouvrir les spécifications, de connaître quelques mots d'Anglais et de lire les commentaires qui expliquent succinctement le rôle de tel ou tel sous-programme ainsi que le rôle des divers paramètres.

Pour trouver ces fichiers, ouvrez le répertoire d'installation de GNAT. Vous devriez tout d'abord trouver un répertoire correspondant à la version de votre compilateur (l'année en fait). Ouvrez-le puis suivez le chemin suivant (il est possible que les noms varient légèrement selon votre système d'exploitation ou la version de votre compilateur) :

lib\gcc\i686-pc-mingw32\4.5.3\adainclude

Convention de nommage

C'est vrai que c'est déconcertant au début, mais vous parviendrez peu à peu à vous retrouver dans cette énorme pile de fichiers. Commencez déjà par les classer par type afin de séparer le corps des spécifications. Vous devriez remarquer que, à quelques rares exceptions, tous les noms de fichier commencent par une lettre suivie d'un tiret. Cette lettre est l'initiale du premier mot du nom de package. Par exemple le package Ada.Text_IO a un nom de fichier commençant par « a- ». La convention est la suivante :

Vous remarquerez ensuite que les points dans Ada.Text_IO ou Ada.Strings.Unbounded sont remplacés par des tirets dans les noms de fichier. Ainsi Ada.Text_IO a un fichier nommé a-textio.ads, Ada.Strings.Unbounded a un fichier nommé a-strunb.ads.

Organiser nos packages

Bien sûr que si. Vous verrez que lorsque vos programmes prendront de l'ampleur, le nombre de packages augmentera lui-aussi. Il deviendra donc important de classer tous ces fichiers pour mieux vous y retrouver. Si le logiciel GPS gère seul l'ensemble du projet, l'IDE Adagide est lui plus rudimentaire : placez par exemple vos packages dans un sous-répertoire nommé « packages » (original non ?). Bien sûr, si vous cherchez à compiler, Adagide vous dira qu'il ne trouve pas vos packages. Il faut donc lui indiquer où ils se situent. Cliquez sur menu Compile > Select Target. Dans la fenêtre qui s'ouvre, choisissez l'onglet Debug settings où vous devriez trouver la ligne Compiler Options. C'est là qu'il vous faudra inscrire : -I./packages. Cette ligne signifie « Inclure (-I) le répertoire ./packages ».

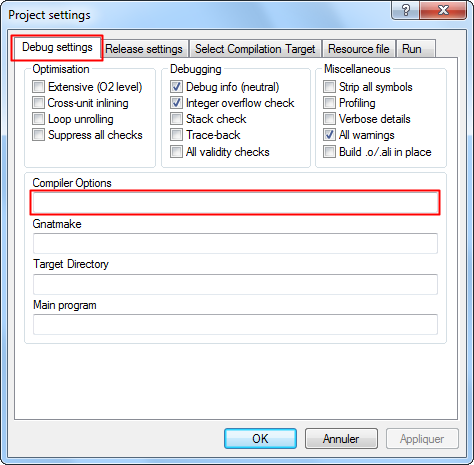
Compilez et construisez votre programme : ça marche !

Petite astuce pour limiter les fichiers générés

Vous avez du remarquer qu'en compilant votre code ou en construisant votre programme, GNAT génère toute une flopée de fichiers aux extensions exotiques : .o, .ali, .bak, .bk.1, .ago … sans parler des copies de vos fichiers sources commençant par b~ ! Et en créant des packages, nous augmentons encore le nombre des fichiers qui seront générés ! Ces fichiers sont utiles pour GNAT et permettent également d'accélérer la compilation ; mais lorsqu'ils sont trop nombreux, cela devient une perte de temps pour vous. Voici une astuce pour faire le ménage rapidement.

Ouvrez un éditeur de texte et copiez-y les commandes suivantes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

del *.o
del *.ali
del *.bk.*
del *.bak
del *.0
del *.1
del *.2
del *.3
del *.4
del *.5
del *.6
del *.7
del *.8
del b~*

Enregistrez ensuite ce fichier texte dans le répertoire de votre programme en lui donnant le nom Commande.bat. Désormais, il suffira que vous double-cliquiez dessus pour qu'un grand ménage soit fait, supprimant tous les fichiers dont l'extension est notée ci-dessus. Remarquez d'ailleurs qu'il n'y a pas d'instruction del gnat.ago afin de conserver ce fichier.

Compléter notre package (exercices)

Cahier des charges

Pour l'heure, notre package ne contient pas grand chose : le type T_Vecteur et une procédure Put(). Nous allons donc le compléter, ce sera un excellent exercice pour appliquer tout ce que nous avons vu et cela nous fournira un package bien utile. De quoi avons-nous besoin ?

• Des procédures d'affichage
• Des procédures de création
• Des fonctions de tri
• Des fonctions pour les opérations élémentaires.

Procédures d'affichage

1

PROCEDURE Put(T : IN T_Vecteur ; FORE : IN integer := 11) ;

Celle-là ne sera pas compliquée : nous l'avons déjà faite. Elle affiche les valeurs contenues dans un T_Vecteur T sur une même ligne. Fore indique le nombre de chiffres à afficher (Fore pour Before = Avant la virgule).

1

PROCEDURE Put_line(T : IN T_Vecteur ; FORE : IN integer := 11) ;

Affiche les valeurs du T_Vecteur T comme Put() et retourne à la ligne.

1

PROCEDURE Put_Column(T : IN T_Vecteur ; FORE : IN integer := 11 ; Index : IN Boolean := true) ;

Affiche les valeurs du T_Vecteur T comme Put() mais en retournant à la ligne après chaque affichage partiel. Le paramètre booléen Index indiquera si l'on souhaite afficher l'indice de la valeur affichée (le numéro de sa case).

Procédures de création

1

PROCEDURE Get(T : IN OUT T_Vecteur) ;

Permet à l'utilisateur de saisir au clavier les valeurs du T_Vecteur T. L'affichage devra être le plus sobre possible. Pas de « Veuillez vous donner la peine de saisir la 1ere valeur du T_Vecteur en question » :

1

PROCEDURE Init(T : IN OUT T_Vecteur ; Val : IN integer := 0) ;

Initialise un tableau en le remplissant de 0 par défaut. Le paramètre Val permettra de compléter par autre chose que des 0.

1
2
3

PROCEDURE Generate(T   : IN OUT T_Vecteur ; 
                   Min : integer := integer'first ; 
                   Max : integer := integer'last) ;

Génère un T_Vecteur rempli de valeurs aléatoires comprises entre Min et Max. Il vous faudra ajouter le package Ada.Numerics.Discrete_random au début de votre fichier .adb !

Fonctions de tri

1

FUNCTION Tri_Selection(T : T_Vecteur) RETURN T_Vecteur ;

Pour l'heure, nous n'avons vu qu'un seul algorithme de tri de tableau : le tri par sélection (ou tri par extraction). Je vous invite donc à en faire un petit copier-coller-modifier. Mais il en existe de nombreux autres. Nous serons donc amenés à créer plusieurs fonctions de tri, d'où le nom un peu long de notre fonction. J'ai préféré le terme français cette fois (Select_Sort n'étant pas très parlant). Peut-être sera-t-il intéressant de créer également les fonctions RangMin ou Echanger pour un usage futur?

Opérations élémentaires

1

FUNCTION Somme(T : T_Vecteur) RETURN integer ;

Renvoie la somme des éléments du T_Vecteur.

1

FUNCTION "+"(Left,Right : T_Vecteur) RETURN T_Vecteur ;

Effectue la somme de deux T_Vecteurs. L'écriture très spécifique de cette fonction (avec un nom de fonction écrit comme un string et exactement deux paramètres Left et Right pour Gauche et Droite) nous permettra d'écrire par la suite T3 := T1 + T2 au lieu de T3 := +(T1,T2) ! On dit que l'on surcharge l'opérateur "+".

1

FUNCTION "*"(Left : integer ; Right : T_Vecteur) RETURN T_Vecteur ;

Effectue le produit d'un nombre entier par un T_Vecteur.

1

FUNCTION "*"(Left, Right : T_Vecteur) RETURN Integer ;

Effectue le produit scalaire de deux T_Vecteurs. Pas de confusion possible avec la fonction précédente car les paramètres ne sont pas de même type.

1
2

FUNCTION Minimum(T : T_Vecteur) RETURN Integer ;
FUNCTION Maximum(T : T_Vecteur) RETURN Integer ;

Renvoient respectivement le plus petit et le plus grand élément d'un T_Vecteur.

Solutions

Voici les packages Integer_Array.adb et Integer_Array.ads tels que je les ai écrits. Je vous conseille d'essayer de les écrire par vous-même avant de copier-coller ma solution, ce sera un très bon entraînement. Autre conseil, pour les opérations élémentaires, je vous invite à lire la sous-partie qui suit afin de comprendre les quelques ressorts mathématiques.

• Integer_Array.adb :

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167

WITH Ada.Integer_Text_IO, Ada.Text_IO, Ada.Numerics.Discrete_Random ;
USE Ada.Integer_Text_IO, Ada.Text_IO ;

package body Integer_Array IS

      --------------------------
      --Procédures d'affichage--
      --------------------------

   PROCEDURE Put (
         T    : IN     T_Vecteur;
         Fore : IN     Integer := 11) IS
   BEGIN
      FOR I IN T'RANGE LOOP
         Put(T(I),Fore) ;
         put(" ; ") ;
      END LOOP ;
   END Put ;

   PROCEDURE Put_Column (
         T    : IN     T_Vecteur;
         Fore : IN     Integer := 11) IS
   BEGIN
      FOR I IN T'RANGE LOOP
         Put(T(I),Fore) ;
         new_line ;
      END LOOP ;
   END Put_Column ;

   PROCEDURE Put_Line (
         T    : IN     T_Vecteur;
         Fore : IN     Integer := 11) IS
   BEGIN
      Put(T,Fore) ;
      New_Line ;
   END Put_line ;

      ------------------------
      --Procédures de saisie--
      ------------------------

   PROCEDURE Init (
         T     :    OUT T_Vecteur;
         Value : IN     Integer := 0) IS
   BEGIN
      T := (OTHERS => Value) ;
   END Init ;

   procedure generate(T : in out T_Vecteur ; 
                      min : in integer := integer'first ; 
                      max : in integer := integer'last) is
      subtype Random_Range is integer range min..max ;
      Package Random_Array is new ada.Numerics.Discrete_Random(Random_Range) ;
      use Random_Array ;
      G : generator ;
   begin
      reset(G) ; 
      T := (others => random(g)) ;
   end generate ;

   procedure get(T : in out T_Vecteur) is
   begin
      for i in T'range loop
         put(integer'image(i) & " : ") ;
         get(T(i)) ;
         skip_line ;
      end loop ;
   end get ;

      --------------------
      --Fonctions de tri--
      --------------------

   function Tri_Selection(T : T_Vecteur) return T_Vecteur is

      function RangMin(T : T_Vecteur ; debut : integer ; fin : integer) return integer is  
         Rang : integer := debut ;  
         Min : integer := T(debut) ;  
      begin 
         for i in debut..fin loop
            if T(i)<Min
               then Min := T(i) ; 
                  Rang := i ;
            end if ; 
         end loop ;  
      return Rang ;  
      end RangMin ;  

      procedure Echanger(a : in out integer ; b : in out integer) is
         c : integer ; 
      begin 
         c := a ; 
         a := b ; 
         b := c ; 
      end Echanger ; 

      Tab : T_Vecteur := T ; 
   begin
      for i in Tab'range loop
         Echanger(Tab(i),Tab(RangMin(Tab,i,Tab'last))) ; 
      end loop ; 
   return Tab ; 
   end Tri_Selection ; 

      ---------------------------
      --Opérations élémentaires--
      ---------------------------

   function Somme(T:T_Vecteur) return integer is
      S : integer := 0 ;
   begin
      for i in T'range loop
         S:= S + T(i) ;
      end loop ;
   return S ;
   end somme ;

   FUNCTION "+" (Left,Right : T_Vecteur) return T_Vecteur is
      T : T_Vecteur ;
   begin
      for i in Left'range loop
         T(i) := Left(i) + Right(i) ;
      end loop ;
   return T ;
   end "+" ;

   FUNCTION "*" (Left : integer ; Right : T_Vecteur) return T_Vecteur is
      T : T_Vecteur ;
   begin
      for i in Right'range loop
         T(i) := Left * Right(i) ;
      end loop ;
   return T ;
   end "*" ;

   FUNCTION "*" (Left,Right : T_Vecteur) return Integer is
      S : Integer := 0 ;
   begin
      for i in Left'range loop
         S := S + Left(i) * Right(i) ;
      end loop ;
   return S ;
   end "*" ;

   FUNCTION Minimum(T : T_Vecteur) return integer is
      min : integer := T(T'first) ; 
   BEGIN
      FOR I in T'range loop
         if T(i)<min
            then min := T(i) ; 
         end if ; 
      end loop ; 
   return min ; 
   end Minimum ; 

   FUNCTION Maximum(T : T_Vecteur) return integer is
      max : integer := T(T'first) ; 
   BEGIN
      FOR I in T'range loop
         if T(i)>max
            then max := T(i) ; 
         end if ; 
      end loop ; 
   return max ; 
   end Maximum ; 

END Integer_Array ;

• Integer_Array.ads :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64

PACKAGE Integer_Array IS

      -------------------------------------
      --Définition des types et variables--
      -------------------------------------

   Taille : CONSTANT Integer := 10;
   TYPE T_Vecteur IS ARRAY(1..Taille) OF Integer ;

      --------------------------
      --Procédures d'affichage--
      --------------------------

   PROCEDURE Put (
         T    : IN     T_Vecteur;
         Fore : IN     Integer := 11);

   PROCEDURE Put_Column (
         T    : IN     T_Vecteur;
         Fore : IN     Integer := 11);

   PROCEDURE Put_Line (
         T    : IN     T_Vecteur;
         Fore : IN     Integer := 11);

      ------------------------
      --Procédures de saisie--
      ------------------------

   PROCEDURE Init (
         T     :    OUT T_Vecteur;
         Value : IN     Integer := 0);

   PROCEDURE Generate (
         T   : IN OUT T_Vecteur;
         Min : IN     Integer := Integer'First;
         Max : IN     Integer := Integer'Last);

   PROCEDURE Get (
         T : IN OUT T_Vecteur);

      --------------------
      --Fonctions de tri--
      --------------------

   function Tri_Selection(T : T_Vecteur) return T_Vecteur ;

      ---------------------------
      --Opérations élémentaires--
      ---------------------------

   function Somme(T:T_Vecteur) return integer ;

   FUNCTION "+" (Left,Right : T_Vecteur) return T_Vecteur ;

   FUNCTION "*" (Left : integer ; Right : T_Vecteur) return T_Vecteur ;

   FUNCTION "*" (Left,Right : T_Vecteur) return Integer ;

   FUNCTION Minimum(T : T_Vecteur) return integer ;

   FUNCTION Maximum(T : T_Vecteur) return integer ;

END Integer_Array ;

Vous remarquerez que j'utilise autant que possible les attributs et agrégats. Pensez que vous serez amenés à réutiliser ce package régulièrement et sûrement aussi à modifier la longueur de nos tableaux T_Vecteur. Il ne faut pas que vous ayez besoin de relire toutes vos procédures et fonctions pour les modifier !

Vecteurs et calcul vectoriel (optionnel)

Qu'est-ce exactement qu'un T_Vecteur ?

Le terme T_Vecteur (ou Vector) n'est pas utilisé par le langage Ada, contrairement à d'autres. Pour Ada, cela reste toujours un ARRAY. Mais des analogies peuvent être faites avec l'objet mathématique appelé « vecteur ». Alors, sans faire un cours de Mathématiques, qu'est-ce qu'un vecteur ?

De manière (très) schématique un T_Vecteur est la représentation d'un déplacement, symbolisé par une flèche :

Ainsi, sur le schéma ci-dessus, le T_Vecteur $\vec{AB}$ se déplace de 3 unités vers la droite et de 1 unité vers le haut. Il représente donc le même déplacement que le T_Vecteur $\vec{CD}$ et on peut écrire $\vec{AB} = \vec{CD}$ . On remarquera que ces vecteurs sont « parallèles », de même « longueur » et dans le même sens. Du coup, on peut dire que ces deux vecteurs ont comme coordonnées : $(3 ; 1)$ ou $\begin {pmatrix} 3 \\ 1 \end{pmatrix}$, ce qui devrait commencer à vous rappeler nos tableaux, non ? Pour les récalcitrants, sachez qu'il est possible en Mathématiques de travailler avec des vecteurs en 3, 4, 5… dimensions. Les coordonnées d'un vecteur ressemblent alors à cela :

$(3 ; 1 ; 5 ; 7 ; 9)$ ou $\begin {pmatrix} 3 \\ 1 \\ 5 \\ 7 \\9 \end{pmatrix}$

Ça ressemble sacrément à nos tableaux T_Vecteurs, non ?

Calcul vectoriel

Plusieurs opérations sont possibles sur les T_Vecteurs. Tout d'abord, l'addition ou Relation de Chasles. Sur le schéma ci-dessus, chacun des vecteurs $\vec{AB}$ ou $\vec{CD}$ a été décomposé en deux vecteurs noirs tracés en pointillés : que l'on aille de A à B en suivant le vecteur $\vec{AB}$ ou en suivant le premier vecteur noir puis le second, le résultat est le même, on arrive en B ! Eh bien, suivre un vecteur puis un autre, cela revient à les additionner.

D'où la formule :

$\begin {pmatrix} 3 \\ 1 \end{pmatrix} = \begin {pmatrix} 3 \\ 0 \end{pmatrix} + \begin {pmatrix} 0 \\ 1 \end{pmatrix}$

On remarque qu'il a suffi d'ajouter chaque coordonnée avec celle « en face ». Il est aussi possible de multiplier un vecteur par un nombre. Cela revient simplement à l'allonger ou à le rétrécir (notez que multipliez un vecteur par un nombre négatif changera le sens du vecteur). Par exemple :

$5 \times \begin {pmatrix} 3 \\ 1 \end{pmatrix} = \begin {pmatrix} 15 \\ 5 \end{pmatrix}$

Troisième opération : le produit scalaire. Il s'agit ici de multiplier deux vecteurs entre eux. Nous ne rentrerons pas dans le détail, ce serait trop long à expliquer et sans rapport avec notre sujet. Voici comment effectuer le produit scalaire de deux vecteurs :

$\begin {pmatrix} 3 \\ 1 \\ 5 \end{pmatrix} \times \begin {pmatrix} 2 \\ 4 \\ 6 \end{pmatrix} = (3 \times 2) + (1 \times 4) + (5 \times 6) = 6 + 4 + 30 = 40$

Bien, nous en avons fini avec l'explication mathématique des vecteurs. Pour ceux qui ne connaissaient pas les vecteurs, ceci devrait avoir quelque peu éclairci votre lanterne. Pour ceux qui les connaissaient déjà, vous me pardonnerez d'avoir pris quelques légèretés avec la rigueur mathématique pour pouvoir «vulgariser» ce domaine fondamental des Maths.

Nous avons maintenant un joli package Integer_Array. Nous pourrons l'utiliser aussi souvent que possible, dès lors que nous aurons besoin de tableaux à une seule dimension contenant des integers. Il vous est possible également de créer un package Integer_Array2D pour les tableaux à deux dimensions. Mais surtout, conserver ce package car nous le complèterons au fur et à mesure avec de nouvelles fonctions de tri, plus puissantes et efficaces, notamment lorsque nous aborderons la récursivité ou les notions de complexité d'algorithme. Lors du chapitre sur la généricité, nous ferons en sorte que ce package puisse être utilisé avec des float, des natural… Bref, nous n'avons pas fini de l'améliorer.

Qui plus est, vous avez sûrement remarqué que ce chapitre s'appelle «La programmation modulaire I». C'est donc que nous aborderons plus tard un chapitre «La programmation modulaire II». Mais rassurez-vous, vous en savez suffisamment aujourd'hui pour créer vos packages. Le chapitre II permettra d'améliorer nos packages et d'aborder les notions d'héritage et d'encapsulation chères à la programmation orientée objet.

En résumé :

• Un package est constitué d'un fichier ads contenant les spécifications de vos fonctions et procédures et, si nécessaire, d'un fichier adb contenant le corps. Ce dernier se distingue par l'utilisation des mots clés PACKAGE BODY.
• Prenez soin de vérifier que les corps des fonctions et procédures correspondent trait pour trait à leurs spécifications car ce sont ces dernières qui feront foi.
• Les types, les variables et constantes globales sont déclarés avec les spécifications des fonctions et procédures dans le fichier ads.
• Éviter d'utiliser des variables globales autant que cela est possible. En revanche, il n'est pas idiot de « globaliser » vos constantes.
• N'hésitez pas à fouiller parmi les packages officiels. Vous y trouverez des pépites qui vous éviteront de réinventer la roue ou vous ouvriront de nouvelles possibilités.

• Les chaînes de caractères
• Sommaire
• Les fichiers