Les pointeurs II

• Les pointeurs I : allocation dynamique
• Sommaire
• Fonctions et procédures II : la récursivité

Après un premier chapitre présentant la théorie sur les pointeurs (ou accesseurs) et l'allocation dynamique, nous allons dans cette seconde partie nous intéresser aux différentes possibilités offertes par le langage Ada : comment pointer sur une variable ou une constante déjà créée ? Comment créer des pointeurs constants ? Comment passer un pointeur en argument dans une fonction ou une procédure ? Comment créer puis manipuler des pointeurs sur des programmes ? C'est ce à quoi nous allons tenter de répondre dans ce chapitre avant d'effectuer quelques exercices d'application.

• Cas général
• Pointeur comme paramètre
• Pointeur sur un programme (optionnel)
• Exercices

Cas général

Pointeurs généralisés : pointer sur une variable

Pour l'instant, nous avons été obligés de pointer sur des valeurs définies par vos propres soins. Nous voudrions désormais pouvoir pointer sur une valeur générée par l'utilisateur ou par le programme, sans que le programmeur en ait eu préalablement connaissance. Une difficulté se pose : lorsque vous créez un «pointeur sur 7», vous demandez à l'ordinateur de créer dans une zone non utilisée de la mémoire un emplacement contenant la valeur 7. Or, pour pointer sur une variable, il ne faudra rien créer ! La variable est créée dès le démarrage de votre programme dans une zone de la mémoire qui a été préalablement réquisitionnée et dont la taille ne varie pas (c'est à cela que servent les déclarations). Il faut donc revoir notre type T_Pointeur pour spécifier qu'il peut pointer sur tout !

1

Type T_Pointeur is access all integer ;

L'instruction ALL permet d'indiquer que l'on peut pointer sur un emplacement mémoire créé en cours de programme (on parle de mémoire dynamique, comme pour l'allocation dynamique), mais aussi sur un emplacement mémoire déjà existant (on parle de mémoire statique) comme une variable.

La déclaration des pointeurs se fera normalement. En revanche, les variables que vous autoriserez à être pointées devront être clairement spécifiées pour éviter d'éventuels problèmes grâce à l'instruction ALIASED.

1
2

Ptr : T_Pointeur ; 
N : aliased integer ;

C'est simple, grâce à un attribut : 'ACCESS !

1
2
3
4

...
begin
   N := 374 ;             --N prend une valeur, ici 374
   Ptr := N'access ;      --Ptr prend comme valeur l'adresse de N

Ainsi, Ptr.all correspondra à la variable N ! Retenez donc ces trois choses :

• le type T_Pointeur doit être généralisé avec ALL ;
• les variables doivent être spécifiées avec ALIASED ;
• l'adresse (ou plus exactement, la référence) peut être récupérée avec l'attribut 'ACCESS.

Pointeur sur une constante et pointeur constant

Pointeur sur une constante

De la même manière, il est possible de créer des pointeurs pointant sur des constantes. Pour cela, notre type T_Pointeur doit être défini ainsi grâce à l'instruction CONSTANT :

1

type T_Pointeur is access constant Integer ;

Notre pointeur et notre constante seront donc déclarées ainsi :

1
2

Ptr : T_Pointeur ; 
N : aliased constant integer := 35 ;

Ptr est déclaré de la même manière que d'habitude. Quant à notre constante N, elle doit être spécifiée comme pouvant être pointée grâce à l'instruction ALIASED ; elle doit être indiquée comme constante avec l'instruction CONSTANT et elle doit être indiquée comme de type Integer (bien sûr) valant 35 (par exemple). Puis, nous pourrons affecter l'adresse mémoire de N à notre pointeur Ptr :

1

Ptr := N'access ;

Attention, ce qui est constant ici, ce n'est pas le pointeur mais la valeur pointée ! Il est donc possible par la suite de modifier la valeur de notre pointeur, par exemple en écrivant le code suivant :

1
2

Ptr := N'access ;
Ptr := M'access ;    --M doit bien-sûr être défini comme aliased constant integer

En revanche il n'est pas possible de modifier la valeur pointée car c'est elle qui doit être constante. Vous ne pourrez donc pas écrire le code suivant :

1
2
3

Ptr := N'Access ; 
Ptr.all := 15 ; 
Ptr.all := N + 1 ;

Pointeur constant

Il est toutefois possible de créer des pointeurs constants. Redéfinissons de nouveau notre type T_Pointeur et nos objets et variables :

1
2
3

type T_Pointeur is access all integer ; 
N : integer ; 
Ptr : constant T_Pointeur := N'access ;

Dans ce cas-ci, c'est le pointeur qui est contant : il pointera sur l'emplacement mémoire de la variable N et ne bougera plus. Maintenant, rien n'empêche N (et donc son emplacement mémoire) de prendre différentes valeurs (d'ailleurs, pour l'heure, Ptr pointe sur N mais N n'a aucune valeur). Exemple d'opérations possibles :

1
2

N := 5 ; 
Ptr.all := 9 ;

Voici un exemple d'opérations interdites dès lors que notre pointeur est constant :

1
2

Ptr := M'access ; 
Ptr := new integer'(13) ;

N'oubliez pas : ici c'est le pointeur qui est constant et donc l'adresse ne doit pas changer (par contre ce qui se trouve à cette adresse peut changer, ou pas).

Pointeur sur pointeur

L'idée semble saugrenue et pourtant elle fera l'objet de notre avant dernier chapitre : créer un pointeur sur un pointeur sur un integer ! Nous devrons donc créer deux types de pointeurs distincts : un type «pointeur sur integer» et un type «pointeur sur pointeur sur integer» !

1
2
3
4
5

type T_Pointeur_Integer is access Integer ; 
type T_Pointeur_Pointeur is access T_Pointeur_Integer ; 

PtrI : T_Pointeur_Integer ;     --PtrI pour Pointeur-Integer
PtrP : T_Pointeur_Pointeur ;    --PtrP pour Pointeur-Pointeur

Cela devrait nous permettre de créer une sorte de liste de pointeurs qui se pointent les uns les autres (mais nous verrons cela plus en détail dans l'avant dernier chapitre) ! Attention, cela apporte quelques subtilités :

1
2
3
4
5

PtrI := new Integer ; 
PtrI.all := 78 ; 

PtrP := new T_Pointeur_Integer ; 
PtrP.all := PtrI ;

PtrP est un pointeur sur un pointeur, donc PtrP.all est lui aussi un pointeur, mais un pointeur sur un entier cette fois ! Si je souhaite modifier cet entier, deux solutions s'offrent à moi : soit utiliser PtrI.all, soit utiliser PtrP de la manière suivante :

1

PtrP.all.all := 79 ;

Il serait même judicieux de reprendre notre code et de ne pas créer de pointeur PtrI. Tout devrait pouvoir être fait avec PtrP. Voyons cela en exemple :

1
2
3
4
5
6
7
8
9

...
   type T_Pointeur_Integer is access Integer ; 
   type T_Pointeur_Pointeur is access T_Pointeur_Integer ; 
   PtrP : T_Pointeur_Pointeur ;    --PtrP pour Pointeur-Pointeur
begin
   PtrP := new T_Pointeur_Integer ;
   PtrP.all := new Integer ; 
   PtrP.all.all := 78 ; 
...

Avec une seule variable PtrP, nous pouvons manipuler 3 emplacements mémoire :

• l'emplacement mémoire du pointeur sur pointeur PtrP;
• l'emplacement mémoire du pointeur sur integer PtrP.all;
• l'emplacement mémoire de l'integer PtrP.all.all qui vaut ici 78 !

Et avec un pointeur sur pointeur sur pointeur sur pointeur sur pointeur… nous pourrions peut-être parvenir à créer, avec une seule variable, une liste d'informations liées les unes aux autres et de longueur infinie (ou tout du moins non contrainte, il suffirait d'utiliser l'instruction NEW à chaque fois que l'on souhaiterait allonger cette liste. Ces «listes» sont la principale application des pointeurs que nous verrons dans ce cours et fera l'objet d'un prochain chapitre ! Alors encore un peu de patience.

Pointeur comme paramètre

Avant de passer aux pointeurs sur les programmes et aux exercices finaux, il nous reste un dernier point à traiter : comment transmettre un pointeur comme paramètre à une fonction ou une procédure ? Supposons que nous ayons deux procédures Lire() et Ecrire() et une fonction Calcul()nécessitant un pointeur sur Integer en paramètre. Voyons tout d'abord comment déclarer nos procédures et fonctions sur des prototypes :

1
2
3

procedure Lire(Ptr : T_Pointeur) ; 
procedure Ecrire(Ptr : T_Pointeur) ; 
function Calcul(Ptr : T_Pointeur) return Integer ;

Voici une autre façon de déclarer nos sous-programmes, permettant de s'affranchir du type T_Pointeur :

1
2
3

procedure Lire(Ptr : access Integer) ; 
procedure Ecrire(Ptr : access Integer) ; 
function Calcul(Ptr : access Integer) return Integer ;

Avec cette seconde façon de procéder, il suffira de fournir en paramètre n'importe quel type de pointeur sur Integer, qu'il soit de type T_Pointeur ou autre. Par la suite, nous pourrons appeler nos sous-programmes de différentes façons :

1
2
3
4
5
6
7
8
9

...
   Ptr : T_Pointeur ; 
   N : aliased Integer := 10 ; 
BEGIN
   Ptr := new Integer ; 
   Lire(Ptr) ; 
   Ecrire(N'access) ; 
   N := Calcul(new integer'(25)) ; 
...

Chacun de ces appels est correct. Mais il faut prendre une précaution : le pointeur que vous transmettez à vos fonctions/procédures doit absolument être initialisé et ne pas valoir NULL ! Faute de quoi, vous aurez le droit à un joli plantage de votre programme.

Seconde remarque d'importance : les pointeurs transmis en paramètres sont de mode IN. Autrement dit, la valeur du pointeur (l'adresse sur laquelle il pointe) ne peut pas être modifiée. Cependant, rien n'empêche de modifier la valeur pointée. Ptr n'est accessible qu'en lecture ; Ptr.all est accessible en lecture ET en écriture ! C'est donc comme si nous transmettions Ptr.all comme paramètre en mode IN OUT. Continuons la réflexion : pour les fonctions, il est normalement interdit de fournir des paramètres en mode OUT ou IN OUT, mais en fournissant un pointeur comme paramètre, cela permet donc d'avoir, dans une fonction, un paramètre Ptr.all en mode IN OUT !

Pointeur sur un programme (optionnel)

Cette dernière partie théorique s'avère plus compliquée que les autres. Si vous pensez ne pas être encore suffisamment au point sur les pointeurs (joli jeu de mot ), je vous en déconseille la lecture pour l'instant et vous invite à vous exercer davantage. Si vous êtes suffisamment aguerris, alors nous allons passer aux chose très, TRÈS sérieuses !

Un exemple simple

Commençons par prendre un exemple simple (simpliste même, mais rassurez-vous, l'exemple suivant sera bien plus ardu). Nous disposons de trois fonctions appelées Double( ), Triple( ) et Quadruple( ) dont voici les spécifications :

1
2
3

function Double(n : integer) return integer ;
function Triple(n : integer) return integer ;
function Quadruple(n : integer) return integer ;

Peu nous importe de savoir comment elles ont été implémentées, ce que l'on sait c'est qu'elles nécessitent un paramètre de type integer et renvoient toutes un integer qui est, au choix, le double, le triple ou le quadruple du paramètre fournit. Seulement nous voudrions maintenant créer une procédure Table( ) qui affiche le double, le triple ou le quadruple de tous les nombres entre a et b (a et b étant deux nombres choisis par l'utilisateur, la fonction choisie l'étant elle aussi par l'utilisateur). Nous aurions besoin que les fonctions double( ), triple( ) ou quadruple( ) puissent être transmise à la procédure Table( ) comme de simples paramètres, ce qui éviterait que notre sous-procédure ait à se soucier du choix effectué par l'utilisateur. Nous voudrions ce genre de prototype :

1
2

procedure Table(MaFonction : function ; 
                a,b : integer) ;

Malheureusement, cela n'est pas possible en tant que tel. Pour arriver à cela, nous allons devoir transmettre en paramètre, non pas une fonction, mais un pointeur sur une fonction. Donc première chose : comment déclarer un pointeur sur une fonction ? C'est un peu compliqué car qu'est-ce qu'une fonction ? C'est avant tout des paramètres d'un certain type qui vont être modifiés afin d'obtenir un résultat d'un certain type. Ainsi, si un pointeur pointe sur une fonction à un paramètre, il ne pourra pas pointer sur une fonction à deux paramètres. Si un pointeur pointe sur une fonction renvoyant un integer, il ne pourra pas pointer sur une fonction renvoyant un float. Donc nous devons définir un type T_Ptr_Fonction qui prenne en compte tout cela : nombre et type des paramètres, type de résultat. Ce qui nous amène à la déclaration suivante :

1
2
3
4

type T_Ptr_Fonction is access function(n : integer) return integer ; 
f : T_Ptr_Fonction ;
--f est la notation mathématique usuelle pour fonction
--mais n'oubliez pas qu'il s'agit uniquement d'un pointeur !

Définissons maintenant notre procédure Table :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

procedure Table(MaFonction : T_Ptr_Fonction ; 
                a,b : integer) is
begin
   for i in a..b loop
      put(i) ; 
      put(" : ") ; 
      put(MaFonction.all(i)) ; 
      new_line ; 
   end loop ; 
end Table ;

Heureusement, le langage Ada nous permet de remplacer la ligne 7 par la ligne ci-dessous pour plus de commodité et de clareté :

1

put(MaFonction(i)) ;

Toutefois, n'oubliez pas que MaFonction n'est pas une fonction ! C'est un pointeur sur une fonction ! Ada nous fait grâce du .all pour les fonctions pointées à la condition que les paramètres soient écrits. Enfin, il ne reste plus qu'à appeler notre procédure Table( ) dans la procédure principale :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

--Choix de la fonction à traiter
   put("Souhaitez-vous afficher les doubles(2), les triples(3) ou les quadruples(4) ?") ; 
   get(choix) ; skip_line ; 
   case choix is
      when 2 => f := double'access ; 
      when 3 => f := triple'access ; 
      when others => f := quadruple'access ; 
   end case ; 

--Choix des bornes de l'intervalle
   put("A partir de ") ; get(a) ; skip_line ; 
   put("jusqu'à ") ; get(b) ; skip_line ; 

--Affichage de la table de a à b de la fonction f choisie
   Table(f,a,b) ;

En procédant ainsi, l'ajout de fonctions Quintuple( ), Decuple( ), Centuple( )… fonctionnant sur le même principe que les précédentes se fera très facilement sans modifier le code de la fonction Table( ), mais uniquement la portion de code où l'utilisateur doit faire un choix entre les fonctions. Cela peut paraître anodin à notre niveau, mais ce petit gain de clarté et d'efficacité devient très important lors de projets plus complexes faisant intervenir plusieurs programmeurs. Celui rédigeant le programme Table( ) n'a pas besoin d'attendre que celui rédigeant les fonctions Double( ), Triple( )… ait terminé, il peut dors et déjà coder sa procédure en utilisant une fonction f théorique.

Un exemple de la vie courante

Ah bon ? Pourtant vous utilisez en ce moment même ce genre de procédé. Alors même que vous lisez ces lignes, votre ordinateur doit gérer une liste de programmes divers et variés. Il vous suffit d'appuyer sur Alt+Ctrl+Suppr sous Windows puis de cliquer sur l'onglet Processus pour voir la liste des processus en cours. Sous Linux, ouvrez la console et tapez la commande ps (pour process status).

Comment votre système d'exploitation fait-il pour gérer plusieurs processus ? Entre Explorer, votre navigateur internet, votre antivirus, l'horloge… sans compter les programmes que vous pourriez encore ouvrir ou fermer, il faut bien que votre système d'exploitation (que ce soit Windows, Linux, MacOS…) puisse gérer une liste changeante de programmes ! C'est, très schématiquement, ce que nous permettent les pointeurs : gérer des listes de longueurs indéfinies (voir le prochain chapitre) de pointeurs vers des programmes alternativement placés en mémoire vive ou traités par le processeur. Rassurez-vous, je ne compte pas vous faire développer un système d'exploitation dans votre prochain TP, je vous propose là simplement une illustration de notre travail.

Un exemple très… mathématique

Ce troisième et dernier exemple s'adresse à ceux qui ont des connaissances mathématiques un peu plus poussées (disons, niveau terminale scientifique). En effet, les fonctions sont un outil mathématique très puissant et très courant. Et deux opérations essentielles peuvent-être appliquées aux fonctions : la dérivation et l'intégration. Je souhaiterais traiter ici l'intégration. Ou plutôt, une approximation de l'intégrale d'une fonction par la méthode des trapèzes.

Pour rappel, et sans refaire un cours de Maths, l'intégrale entre a et b d'une fonction f correspond à l'aire comprise entre la courbe représentative de la fonction (entre a et b) et l'axe des abscisses. Pour approximer cette aire, plusieurs méthodes furent inventées, notamment la méthode des rectangles qui consiste à approcher l'aire de cette surface par une série de rectangles. La méthode des trapèzes consiste quant à elle à l'approximer par une série de trapèzes rectangles.

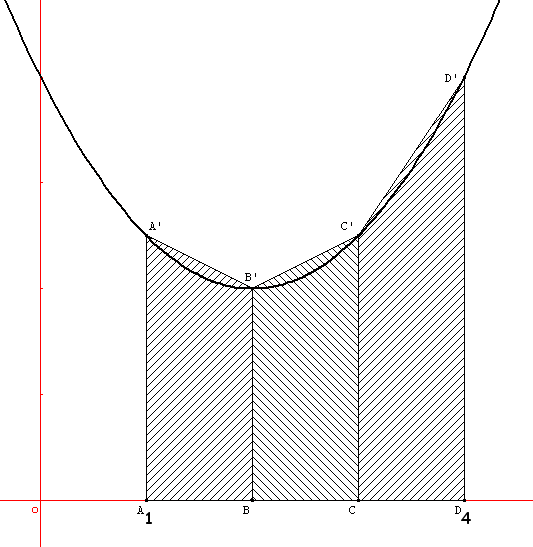
Dans l'exemple précédent, on a cherché l'aire sous la courbe entre 1 et 4. L'intervalle [ 1 ; 4 ] a été partagé en 3 sous-intervalles de longueur 1. La longueur de ces sous-intervalles est appelée le pas. Comment calculer l'aire du trapèze ABB'A' ? De la manière suivante : ${{AA' + BB'} \over2} \times AB$. Et on remarquera que $AA' = f(1)$, $BB' = f(1+pas)$, $CC' = f(1+2 \times pas)$ …

Nous allons donc définir quelques fonctions dont voici les prototypes :

1
2
3

function carre(x : float) return float ;
function cube(x : float) return float ; 
function inverse(x : float) return float ;

Nous allons également définir un type T_Pointeur :

1

type T_Pointeur is access function(x : float) return float ;

Nous aurons besoin d'une fonction Aire_Trapeze et d'une fonction Integrale dont voici les prototypes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

--aire_trapeze() ne calcule l'aire que d'un seul trapèze
--f est la fonction étudiée
--x le "point de départ" du trapèze
--pas correspond au pas, du coup, x+pas est le "point d'arrivée" du trapèze
function aire_trapeze(f : T_Pointeur ; x : float ; pas : float) return float ;

--integrale() effectue la somme des aires de tous les trapèzes ainsi que le calcul du pas
--f est la fonction étudiée
--min et max sont les bornes
--nb_inter est le nombre de sous-intervalles et donc de trapèzes, 
--ce qui correspond également à la précision de la mesure
function integrale(f: T_pointeur ; 
                      min,max: float ; 
                      nb_inter : integer) return float is

Je vous laisse le soin de rédiger seuls ces deux fonctions. Cela constituera un excellent exercice sur les pointeurs mais aussi sur les intervalles et le pas. Il ne reste donc plus qu'à appeler notre fonction integrale( ) :

1
2
3
4
5

--a,b sont des float saisis par l'utilisateur représentant les bornes de l'intervalle d'intégration
--i est un integer saisi par l'utilisateur représentant le nombre de trapèzes souhaités
integrale(carre'access,a,b,i) ; 
integrale(cube'access,a,b,i) ; 
integrale(inverse'access,a,b,i) ;

Bon allez ! Je suis bon joueur, je vous transmets tout de même un code source possible. Attention, ce code est très rudimentaire, il ne teste pas si la borne inférieure est bel et bien inférieure à la borne supérieure, rien n'est vérifié quant à la continuité ou au signe de la fonction étudiée… bref, il est éminemment perfectible pour un usage mathématique régulier. Mais là, pas la peine d'insister, vous le ferez vraiment tous seuls.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69

with ada.Text_IO, ada.Integer_Text_IO, ada.Float_Text_IO ; 
use ada.Text_IO, ada.Integer_Text_IO, ada.Float_Text_IO ; 

procedure integration is

      ---------------------------
      --    Fonctions de x     --
      ---------------------------
      
   function carre(x : float) return float is
   begin
      return x**2 ; 
   end carre ; 
   
   function inverse(x:float) return float is
   begin
      return 1.0/x ; 
   end inverse ; 
   
   function cube(x:float) return float is
   begin
      return x**3 ; 
   end cube ; 


      ------------------
      --    Types     --
      ------------------

   type T_Pointeur is access function (x : float) return float ; 

      -------------------------
      --    Fonctions de f   --
      -------------------------

   function aire_trapeze(f : T_Pointeur ; x : float ; pas : float) return float is
   begin
      return ((f.all(x)+f(x+pas))/2.0)*pas ;
   end aire_trapeze ; 

   function integrale(f: T_pointeur ; min,max: float ; nb_inter : integer) return float is
      res : float := 0.0 ; 
      pas : float ; 
   begin
      pas := (max-min)/float(nb_inter) ; 
      for i in 0..nb_inter-1 loop
         res := res + aire_trapeze(f,min+float(i)*pas,pas) ; 
      end loop ; 
   return res ; 
   end integrale ; 

      -------------------------------
      --    Procédure principale   --
      -------------------------------

   a,b : float ; 
   i : integer ; 
begin
   put("Entre quelles valeurs souhaitez-vous integrer les fonctions ?") ; 
      get(a) ; get(b) ; skip_line ; 
   put("Combien de trapezes souhaitez-vous construire ?") ; 
      get(i) ; skip_line ; 
   put("L'integrale de la fonction carre est : ") ; 
      put(integrale(carre'access,a,b,i),Exp=>0) ; new_line ; 
   put("L'integrale de la fonction inverse est : ") ; 
      put(integrale(inverse'access,a,b,i),Exp=>0) ; new_line ;
   put("L'integrale de la fonction cube est : ") ; 
      put(integrale(cube'access,a,b,i),Exp=>0) ; new_line ; 
end integration ;

Exercices

Exercice 1

Énoncé

Voici un programme tout ce qu'il y a de plus simple :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

with ada.Text_IO, ada.Integer_Text_IO ; 
use ada.Text_IO, ada.Integer_Text_IO ; 

procedure programme is
   n,m : integer ; 
begin
   Put("Choisissez un nombre n :") ; get(n) ; skip_line ; 
   Put("Choisissez un nombre m :") ; get(m) ; skip_line ; 
   Put("La somme des nombres choisis est ") ; 
   Put(n+m) ; 
end programme ;

Vous devez modifier ce code de façon à changer le contenu des variables n et m, sans jamais modifier les variables elles-mêmes. Ainsi, le résultat affiché sera faux.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

with ada.Text_IO, ada.Integer_Text_IO ; 
use ada.Text_IO, ada.Integer_Text_IO ; 

procedure programme is
   n,m : aliased integer ; 
   type T_Pointeur is access all integer ; 
   P : T_Pointeur ; 
begin

   Put("Choisissez un nombre n :") ; get(n) ; skip_line ; 
       P := n'access ; 
       P.all := P.all + 1 ;
   Put("Choisissez un nombre m :") ; get(m) ; skip_line ; 
       P := m'access ; 
       P.all := P.all * 3 ;
   Put("La somme des nombres choisis est ") ; 
   Put(n+m) ; 
end programme ;

Exercice 2

Énoncé

Reprenez l'exercice précédent en remplaçant les deux variables n et m par un tableau T de deux entiers puis, en modifiant ses valeurs uniquement à l'aide d'un pointeur.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

with ada.Text_IO, ada.Integer_Text_IO ;
use ada.Text_IO, ada.Integer_Text_IO ;

procedure programme is
   type T_Tableau is array(1..2) of integer ; 
   type T_Pointeur is access all T_Tableau ;
   T : aliased T_Tableau ; 
   P : T_Pointeur ;
begin
   Put("Choisissez un nombre n :") ; get(T(1)) ; skip_line ;
   Put("Choisissez un nombre m :") ; get(T(2)) ; skip_line ;
       P := T'access ; 
       P.all(1):= P.all(1)*18 ; 
       P.all(2):= P.all(2)/2 ; 
   Put("La somme des nombres choisis est ") ;
   Put(T(1)+T(2)) ;
end programme ;

Exercice 3

Énoncé

Reprenez le premier exercice, en remplaçant les deux variables n et m par un objet de type structuré comportant deux composantes entières puis, en modifiant ses composantes uniquement à l'aide d'un pointeur.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

with ada.Text_IO, ada.Integer_Text_IO ;
use ada.Text_IO, ada.Integer_Text_IO ;

procedure programme is
   type T_couple is 
   record
      n,m : integer ; 
   end record ; 
   type T_Pointeur is access all T_couple ;
   Couple : aliased T_couple ; 
   P : T_Pointeur ;
begin
   Put("Choisissez un nombre n :") ; get(couple.n) ; skip_line ;
   Put("Choisissez un nombre m :") ; get(couple.m) ; skip_line ;
       P := Couple'access ; 
       P.all.n:= P.all.n**2 ; 
       P.all.m:= P.all.m mod 3 ; 
   Put("La somme des nombres choisis est ") ;
   Put(Couple.n + Couple.m) ;
end programme ;

1
2

P.n:= P.n**2 ; 
P.m:= P.m mod 3 ;

Exercice 4

Énoncé

Reprenez le premier exercice. La modification des deux variables n et m se fera cette fois à l'aide d'une procédure dont le(s) paramètres seront en mode IN.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

with ada.Text_IO, ada.Integer_Text_IO ;
use ada.Text_IO, ada.Integer_Text_IO ;

procedure programme is
   procedure modif(P : access integer) is
   begin
      P.all := P.all*5 + 8 ; 
   end modif ; 

   n,m : aliased integer ;
begin

   Put("Choisissez un nombre n :") ; get(n) ; skip_line ;
       modif(n'access) ; 
   Put("Choisissez un nombre m :") ; get(m) ; skip_line ;
       modif(m'access) ; 
   Put("La somme des nombres choisis est ") ;
   Put(n+m) ;
end programme ;

Exercice 5 (Niveau Scientifique)

Énoncé

Rédigez un programme calculant le coefficient directeur de la sécante à la courbe représentative d'une fonction f en deux points A et B. À partir de là, il sera possible de réaliser une seconde fonction qui donnera une valeur approchée de la dérivée en un point de la fonction f.

Par exemple, si $f(x) = x^2$, alors la fonction Secante(f,2,7) renverra ${{7^2 - 2^2}\over{7-2}} = 9$. La fonction Derivee(f,5) renverra quant à elle ${(5+h)^2 - 5^2}\over{h}$ où h devra être suffisamment petit afin d'améliorer la précision du calcul.

Solution

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

with ada.Text_IO, ada.Float_Text_IO, ada.Integer_Text_IO ; 
use ada.Text_IO, ada.Float_Text_IO, ada.Integer_Text_IO ; 

procedure derivation is

   type T_Ptr_Fonction is access function(x : float) return float ; 
   
   function carre (x : float) return float is begin
      return x**2 ; 
   end carre ; 
   
   function cube(x : float) return float is begin
      return x**3 ; 
   end cube; 
   
   function inverse(x : float) return float is begin
      return 1.0/x ; 
   end inverse; 

   function secante(f : T_Ptr_Fonction ; 
                    a : float ;
                    b : float ) return float is
   begin
      return (f(b)-f(a))/(b-a) ; 
   end secante ; 
   
   function derivee(f : T_Ptr_Fonction ; 
                    x : float ; 
                    precision : float := 0.000001) return float is
   begin
      return secante(f,x,x+precision) ; 
   end derivee ; 

   choix : integer := 1 ; 
   f : T_Ptr_Fonction ; 
   x: float ; 
begin
   loop
      put("Quelle fonction souhaitez-vous deriver ? Inverse(1), Carre(2) ou Cube(3) .") ; 
      get(choix) ; skip_line ; 
      case choix is
         when 1 => f := inverse'access ; 
         when 2 => f := carre'access ; 
         when 3 => f := cube'access ; 
         when others => exit ; 
      end case ; 
      put("Pour quelle valeur de x souhaitez-vous connaitre la derivee ?") ; 
      get(x) ; skip_line ;
      put("La derivee vaut environ") ; put(derivee(f,x),Exp=>0,Aft=>3) ; put(" pour x =") ; put(x,Exp=>0,Aft=>2) ; 
      new_line ; new_line ; 
   end loop ; 
end derivation ;

Bien, si vous réalisez ces exercices c'est que vous devriez être venus à bout de ces deux chapitres éprouvants. Il est fort possible que vous soyez encore assaillis de nombreuses questions. C'est pourquoi je vous conseille de pratiquer. Ce cours vous a proposé de nombreux exercices, il n'est peut-être pas inutile de reprendre des exercices déjà faits (affichage de tableau, de rectangles…) et de les retravailler à l'aide des pointeurs car cette notion est réellement compliquée. N'hésitez pas non plus à relire le cours à tête reposée.

Si d'aventure vous pensez maîtriser les pointeurs, alors un véritable test vous attend au chapitre 10. Nous mettrons les pointeurs en pratique en créant avec nos petites mains un nouveau type de donnée et les outils pour le manipuler : les types abstraits de donnée ! Là encore, ce sera un chapitre complexe, mêlant théorie et pratique. Mais avant cela nous allons aborder une notion difficile également : la récursivité.

En résumé :

• Pour pointer sur des variables (en mémoire statique) vous devrez indiquer, lors de la déclaration du type, IS ACCESS ALL.
• Pour qu'une variable puisse être pointée, il faudra l'indiquer par le terme ALIASED
• Avec un pointeur constant, les données pointées peuvent être modifiées mais pas l'adresse. Avec un pointeur sur une constante ce sera le contraire.
• Le passage en paramètre d'un pointeur à une fonction permet d'avoir accès aux données pointées en lecture comme en écriture. Un paramètre en mode ACCESS est équivalent à un paramètre en mode IN OUT.
• Il est possible de déclarer des pointeurs sur des fonctions ou des procédures.

• Les pointeurs I : allocation dynamique
• Sommaire
• Fonctions et procédures II : la récursivité