C'est bien gentil ces calculs, mais comment peut-on être certain que cela marche vraiment ?
Depuis Thalès, les mathématiques ne sont plus un simple catalogue de trucs et astuces. L'exigence de démonstration s'est imposée et toute affirmation doit être prouvée non pas sur quelques exemples bien choisis mais dans des cas généraux pouvant être appliqués à n'importe quelle situation particulière. Ainsi, tant qu'une affirmation n'est pas prouvée, elle reste dans la famille des conjectures mathématiques. Si donc la propriété que nous étudions porte le titre honorifique de "théorème", c'est bien qu'elle a été prouvée. Et non contente de l'avoir prouvée, la communauté mathématique s'est même amusée à fournir des centaines de démonstration. Je vous propose donc d'en découvrir quelques-unes.
- Démonstration d'Euclide par les triangles de même aire
- Démonstration de Liu Hui par découpage
- Démonstration par les triangles semblables
Démonstration d'Euclide par les triangles de même aire
Une histoire d'aires
Chose promise, chose due ! Je vous présente désormais une démonstration du théorème de Pythagore. Comme dit plus haut, nous ne disposons d'aucun écrit signé de la main de Pythagore. La démonstration que je vous propose ici est due à un autre mathématicien postérieur : Euclide d'Alexandrie. Pour prouver le théorème, nous allons utiliser la figure ci-dessous :
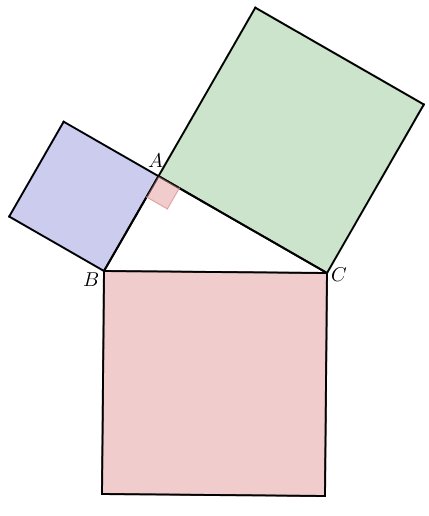
En effet, lorsque l'on calcule $AB^2$, on calculer en réalité l'aire de carré bleu. De même $AC^2$ sera l'aire du carré vert et $BC^2$ l'aire du rouge. Ainsi, prouver la formule de Pythagore $AB^2 + AC^2 = BC^2$ revient à montrer l'égalité suivante :
Euclide commence sa démonstration en découpant le triangle rectangle et le carré rouge. Pour cela, il trace la hauteur issue de A, partageant ainsi le grand carré rouge en deux rectangles vert et bleu.
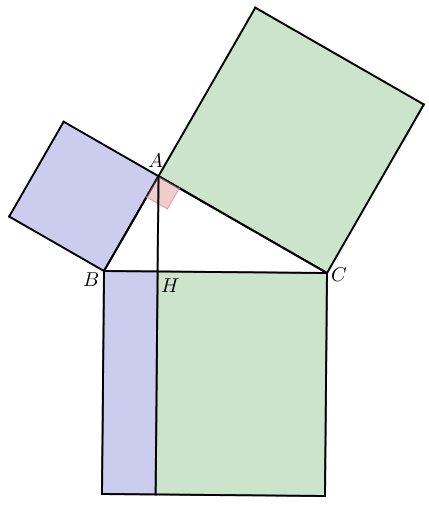
Son idée est que le carré bleu a la même aire que le rectangle bleu et que le carré vert a la même aire que le rectangle vert. S'il parvient à montrer cela, alors c'est gagné ! Mais montrer l'égalité des aires de deux quadrilatères est plutôt compliqué. Euclide va donc préférer utiliser des triangles et utiliser une propriété que je vous propose de découvrir.
Déformez, déformez ! Il restera toujours la même aire.
Si on déplace un sommet d'un triangle parallèlement au côté opposé, alors le triangle obtenu a la même aire que le triangle initial.

La raison est bien simple, la hauteur et la base de tous ces triangles sont identiques. Et comme l'aire d'un triangle se calcule à l'aide de la formule ${\text{Base} \times \text{Hauteur}}\over 2$, tous ces triangles ont la même aire.
La mise en œuvre
Euclide va donc appliquer ce principe au demi-carré bleu :

- Euclide fait glisser l'un des sommets jusqu'en dehors du carré. Il obtient ainsi un triangle "plus allongé" mais de même aire.
- Ceci fait, il fait pivoter le nouveau triangle de 90° pour en obtenir un troisième qui a toujours la même aire.
- Enfin, Euclide recommence le premier procédé et fait glisser un sommet pour reconstituer un demi-rectangle bleu.
- Le demi-rectangle bleu obtenu après toutes ces transformations a donc exactement la même aire que le demi-carré bleu initial !
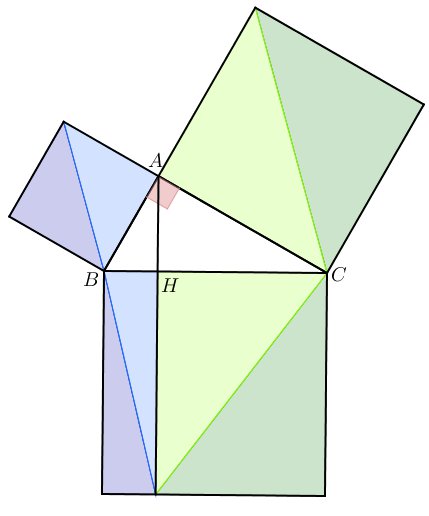
Euclide put ainsi en déduire que le carré bleu et le rectangle bleu avaient la même aire. Il suffisait de recommencer ces transformations avec le carré et le rectangle verts pour constater que la somme des aires des deux petits carrés valait l'aire du grand :
Démonstration de Liu Hui par découpage
Comprendre le puzzle chinois
Intéressons-nous maintenant à la démonstration que fournit le traité mathématique chinois Les neufs chapitres sur l'art mathématique. Ce traité, apparu vers le IIème siècle avant JC, fut plus tard analysé par le mathématicien Liu Hui qui l'annota et le compléta de quelques démonstrations. La démonstration qu'il fournit du théorème de Pythagore (appelé Théorème de Gougu en Chine), est très différente des démonstrations occidentales et repose sur l'idée du découpage des figures (à la façon des célèbres origamis et kirigamis japonais).
Gougu n'est pas le nom d'un mathématicien chinois ! Cela pourrait être traduit par "Théorème des bases et hauteurs".

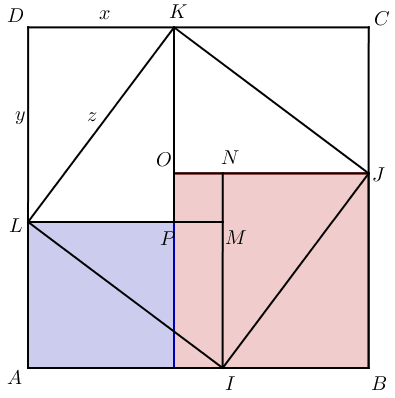
Comme vous pouvez le voir sur l'image ci-dessus, la figure utilisée par Liu Hui est fort différente de celle d'Euclide. La démonstration est fort simple, mais il faut au préalable comprendre les enjeux contenus dans cette figure. Commençons par nommer les sommets de la figure :
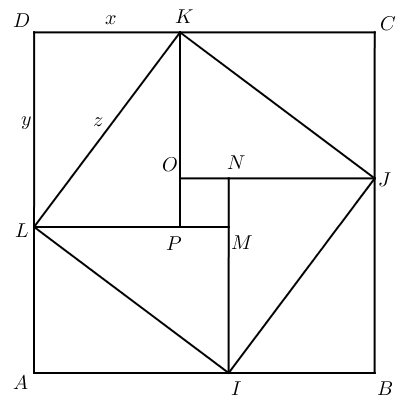
Il y a beaucoup de triangles rectangles identiques dans cette figure, on s'y perd un peu : DLK, LKP, KCJ, KOJ, LAI, LMI, INJ et IJB sont tous des triangles rectangles de longueurs $x, y, z$. Vous constatez qu'ils sont groupés par paires afin de former 4 rectangles (AIML, BJNI, CKOJ et DLPK). Ces 4 rectangles sont disposez afin de former un grand carré extérieur ABCD et un petit carré intérieur MNOP. De plus, les hypoténuses des triangles rectangles forment un carré médian IJKL.
Tu es sûr que IJKL est un carré ? Je me doute bien qu'il a 4 côtés égaux, mais il n'a pas forcément d'angles droit.
Vous savez sûrement que la somme des angles d'un triangle vaut 180° ? On peut préciser cette propriété pour les triangles rectangles. Ceux-ci ayant obligatoirement un angle de 90°, la somme des deux autres angles vaut donc $180-90=90°$. On dit alors que les angles aigus d'un triangle rectangle sont complémentaires. Si on regarde alors la figure ci-dessus, on constate par exemple que les angles $\widehat {LKP}$ et $\widehat {OKJ}$ sont complémentaires : IJKL a donc bien 4 angles droits.
Si l'on prend le triangle rectangle DLK, alors notre but est de montrer que $DL^2 + DK^2 = LK^2$. Mais pour limiter les confusions dans toutes ces lettres, nous allons reformuler cette égalité en $x^2 + y^2 = z^2$. On comprend alors que $z^2$ correspond à l'aire du carré médian IJKL. Mais alors, à quoi correspondent $x^2$ et $y^2$ ? C'est moins évident. Il faut en fait tracer deux nouveaux carrés, par exemple un de côté [JB] dont l'aire vaudra $y^2$ et un côté [LP] dont l'aire vaudra $x^2$.
Reconstituer le puzzle
Maintenant, démontrer que $x^2 + y^2 = z^2$ revient à montrer qu'en déplaçant certaines pièces des carrés rouges et bleus, on parvient à reformer le carré IJKL. Il ne s'agit ni plus ni moins que d'un jeu de tangram, vous êtes donc à même de trouver les mouvements à effectuer par vous-même. Si vous n'y êtes pas arrivés, sachez qu'il suffit de déplacer les triangles IJB et LIA comme expliqué ci-dessous :
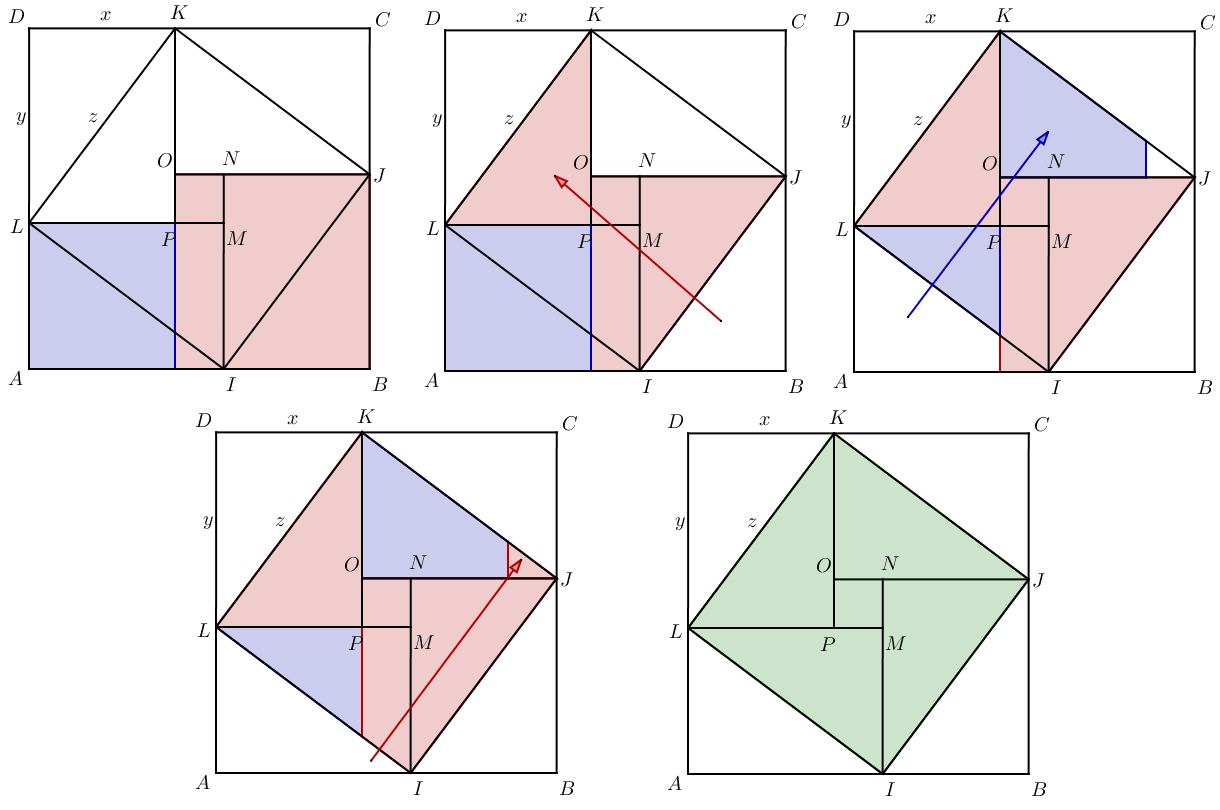
Cette démonstration par découpage semble très différente de la précédente, pourtant de très nombreuses démonstrations du théorème de Pythagore sont basées sur ce principe.
Démonstration par les triangles semblables
Qu'appelle-t-on des triangles semblables ?
On dit que des triangles sont semblables s'ils ont la même forme, c'est-à-dire qu'ils ont des angles égaux et des longueurs proportionnelles. Sur la figure ci-dessous, on constate que les deux premiers triangles ont des longueurs différentes mais une forme similaire, contrairement au troisième qui partage quelques longueurs avec le premier mais dont la forme est plus "étirée".
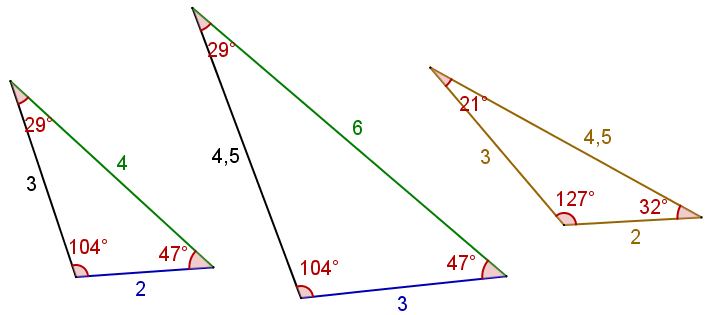
On dit que les deux premiers triangles sont semblables :
- ils ont les mêmes angles,
- le deuxième triangle est 1,5 fois plus grand que le premier. Le nombre 1,5 est appelé coefficient d'agrandissement.
Le périmètre du premier triangle est égal à $2+3+4 = 9$ et le périmètre du second est égal à $3+4,5+6 = 13,5$. Mais on peut remarquer que $9 \times 1,5 = 13,5$. Cet exemple nous permet de constater que si deux triangles sont semblables et liés par un coefficient d'agrandissement $k$, alors leurs périmètres sont eux aussi liés par ce même coefficient $k$.
Logique ? Alors venons-en aux aires. Pour cela, nous allons utiliser notre bon vieux triangle (3;4;5). Le calcul de l'aire d'un triangle rectangle se fait facilement grâce à la formule :
Prenons maintenant un triangle semblable deux fois plus grand : (6;8;10). Son aire devient : $A = \frac {l \times L}{2} = \frac {6 \times 8}{2} = 24$. On obtient une aire non pas 2 fois plus grande mais 4 fois ! Réessayons avec un triangle trois fois plus grand : (9;12;15). L'aire vaut alors $A = \frac {l \times L}{2} = \frac {9 \times 12}{2} = 54$, soit une valeur 9 fois plus grande que prévue. On peut généraliser ce constat : si deux triangles sont semblables et liés par un coefficient d'agrandissement $k$, alors leurs aires sont liées par un coefficient $k^2$.
Cela signifie qu'un triangle dont les côtés sont $5$ fois plus grands qu'un autre aura une aire $5^2=25$ fois plus grande.
Reredémontrons
Pour notre troisième démonstration, nous allons faire apparaître des triangles semblables en traçant la hauteur issue de l'angle droit. Ainsi, sur la figure ci-dessous, le triangle ABC rectangle en B est partagé en deux triangles ABH et BHC eux aussi rectangles.
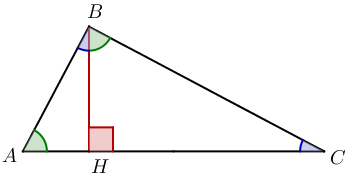
Commençons par expliquer pourquoi ces trois triangles sont semblables. Nous avons vu dans la précédente démonstration que les angles aigus d'un triangle rectangle sont complémentaires (rappel : leur somme vaut 90°). Autrement dit, dans le triangle ABC $\color{blue}\widehat {ACB} \color{black}= 90 - \color{green}\widehat{BAC}$. Mais dans le triangle ABH, cette propriété nous donne $\color{blue}\widehat {ABH} \color{black}= 90 - \color{green}\widehat{BAC}$, la même valeur ! Donc $ \color{blue}\widehat {ACB} = \widehat{ABH}$. Les triangles ABH et ABC ont dont les mêmes angles (un angle droit, un vert et un bleu), ils sont donc semblables. Le même raisonnement peut être fait avec le triangle BHC.
Pour y voir plus clair entre les différentes longueurs en situation de proportionnalité, dressons un tableau :
Le fait que les deux première lignes soient proportionnelles nous permet d'écrire l'égalité de rapport suivante en divisant la première ligne par la seconde : ${AC \over AB} = {AB \over AH} \color{grey}( = {BC \over BH})$. En effectuant un produit en croix entre les deux premières fractions, on obtient que $\color{red}AB^2 = AC \times AH$.
De même, on obtient l'égalité de rapport suivante en divisant la première ligne par la troisième : ${AC \over BC} \color{grey}(= {AB \over BH} )\color{black} = {BC \over HC}$. Le produit en croix entre la première et la dernière fraction donne alors $\color{blue}BC^2 = AC \times HC$. Maintenant que nous avons fait apparaître les carrés des cathètes, additionnons les deux égalités obtenues :
Supplément
Vous aurez peut-être remarqué que nous n'avons pas établi d'égalité de rapport entre la deuxième et la troisième ligne ? Cette égalité ne nous aurait avancé à rien pour la démonstration du théorème de Pythagore. Toutefois, elle apporte un résultat intéressant. Cette égalité est : $\color{grey}({AB \over BC} =) \color{black} {AH \over BH} = {BH \over HC}$. Le produit en croix nous donne enfin :
Nous obtenons ainsi une formule permettant de calculer la hauteur issue de l'angle droit en ne connaissant que l'emplacement du point H sur l'hypoténuse. Mieux que cela ! La hauteur issue de l'angle droit est égale à la moyenne géométrique des distances à gauche et à droite du pied de la hauteur sur l'hypoténuse.
Lorsque nous connaissons deux nombres $x$ et $y$, nous calculons leur moyenne ainsi : ${x + y}\over 2$. Cette moyenne n'est en fait qu'une moyenne parmi d'autres et s'appelle plus exactement la moyenne arithmétique. Une autre moyenne possible est la moyenne géométrique qui se calcule ainsi :$\sqrt{x \times y}$. Mais il en existe d'autres encore comme la moyenne harmonique ($2 \over {\frac 1 x + \frac 1 y}$) ou la moyenne quadratique ($\sqrt{\frac{x^2 + y^2} 2}$).
Si ce petit challenge mathématique vous a plus, sachez que le théorème de Pythagore est sûrement celui qui a le plus de démonstrations à son actif. Vous en trouverez à foison sur Internet ou dans les livres, datant de diverses époques et apparue aux quatre coins de la planète. Il existe même une démonstration découverte par un président des États-Unis à ses heures perdues.