Mais alors, hormis la démonstration de "son" théorème, Pythagore n'a jamais fait de science ?
Ce n'est pas non plus ce que j'ai dit. Cette communauté quasi-religieuse a également apporté beaucoup aux sciences. Nous allons voir ici quelques exemples (sans volonté d'être exhaustif) mais gardez toujours à l'esprit que la transmission orale et le secret étaient de règle chez les pythagoriciens et que par conséquent, nous ne possédons aucun document original. Les écrits dont nous disposons sont plus tardifs et attribuent très certainement les découvertes de certains pythagoriciens à leur maître.
Musique
L'une des découvertes les plus marquantes de Pythagore, étonnamment, concerne la Musique. Cela semble aujourd'hui surprenant, mais durant l'Antiquité et le Moyen-Âge, la Musique était considéré comme une matière scientifique. L'enseignement était basé sur les 7 arts libéraux qui se décomposaient ainsi : le Trivium qui comprenait la grammaire, la dialectique et la rhétorique (les lettres en quelques sortes) ; le Quadrivium qui comprenait la géométrie, l'arithmétique, l'astronomie et … la musique (les sciences comme je vous le disais). On commence alors à comprendre que si Pythagore voyait des nombres dans tout l'univers ou dans toutes les figures géométriques, il devait bien en trouver également dans les odes et les chants.
Si la vision pythagoricienne a échoué à comprendre bien des phénomènes, elle a toutefois été très clairvoyante en matière de Musique. La légende raconte que Pythagore fut un jour dérangé par le bruit que causait le forgeron. S'approchant et observant, il se rendit compte que les sons émis par les coup de marteau de l'artisan étaient plus ou moins graves, selon que celui-ci frappait une lame de de métal plus ou moins longue. Plus important que cela encore, Pythagore a compris un phénomène important : une lame de métal deux fois plus longue qu'une autre émet un son certes plus grave, mais correspondant à la même note ! Autrement dit, si une corde de guitare (ou de lyre pour l'époque) émet un Do lorsqu'on la pince, alors une corde identique deux fois plus longue émettra également un Do mais plus grave :
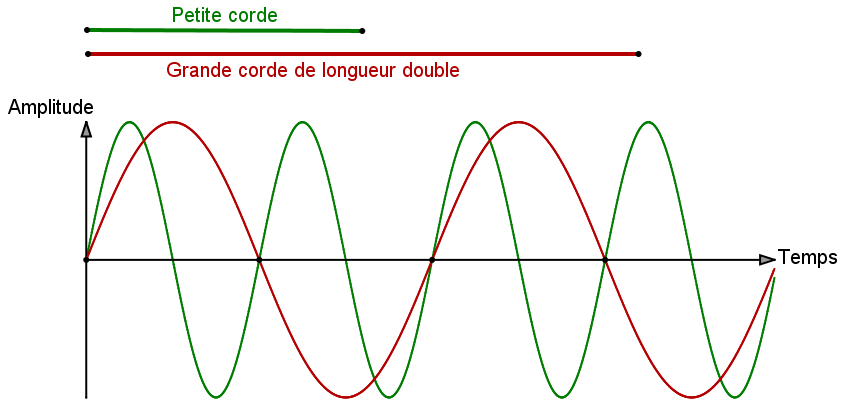
En termes actuels, nous dirions que plus la corde est longue plus la fréquence de ses vibrations diminue. Cela apparaît sur le schéma ci-dessus : la corde rouge émet une vibration plus longue, de grosses et lourdes vagues alors que la petite corde verte émet des vaguelettes de même amplitude, mais bien plus rapides entraînant un son plus aigu. Ces vaguelettes (appelées sinusoïdes) se coupent de manière régulière ce qui implique que la note émise est la même.
Mais alors comment faire une autre note qu'un Do ?
C'est là que le génie de Pythagore a frappé. Il a compris qu'il ne fallait pas prendre n'importe quelle longueur intermédiaire. Supposons que l'on dispose d'une corde émettant un joli Do. Diviser sa longueur par 2 émettrait un Do plus aigu, ce n'est pas ce que nous voulons. Alors en bon aficionado des nombres, Pythagore a décidé de prendre les deux tiers de la corde ! Et, ô miracle, le son était également très joli ! Il obtint ainsi un Sol ! Et avec les trois quarts de la corde ? Il obtenait un joli Fa. Les notes de musique étaient donc liées à des rapports de longueurs fractionnaires. Voilà qui n'était pas pour déplaire aux pythagoriciens.
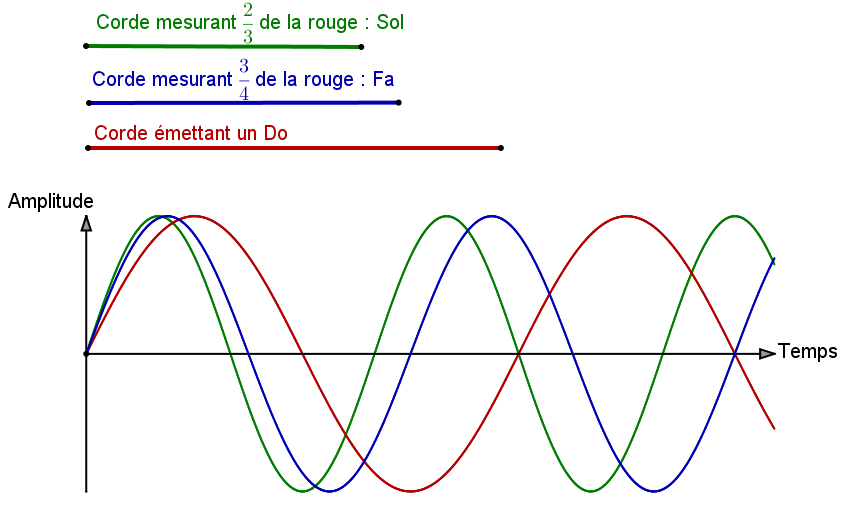
On observe sur ce second schéma que les sinusoïdes ne se coupent plus aussi régulièrement que la fois précédente : les notes sont biens distinctes.
Arithmétique
Nombres géométriques
Les pythagoriciens, nous l'avons vu, voyaient des nombres partout et les entouraient de toute une mystique. Et par nombre, il faut bien comprendre "nombre entier ou fraction". Il est donc logique que leur sujet d'étude favori ait été l'arithmétique, la science des nombres entiers et rationnels, quoiqu'ils l'aient souvent confondue avec l'arithmologie, sorte d'astrologie des nombres. Je vous ai déjà expliqué qu'ils voyaient les figures comme des nombres et les nombres comme des figures. Leur premier "jeu" à donc consister à classer les nombres selon différents catégories géométriques. Prenons un exemple simple : les nombres carrés. Un nombre x est dit carré si avec x pièces de monnaie, on peut dessiner un carré plein. Par exemple, 25 est un nombre carré puisqu'on peut réaliser 5 lignes de 5 pièces, formant ainsi un carré. Mais un petit dessin vaut mieux qu'un long discours :
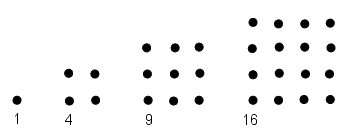
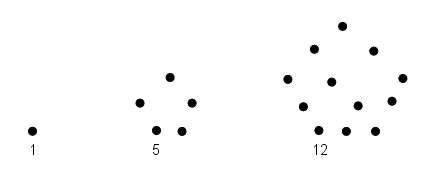
Ainsi, 1, 4, 9, 16, 25, 36 … sont des nombres carrés. On retrouve de façon claire les résultats de 12, 22, 32, 42, 52, 62 … Mais on peut également remarquer qu'il suffit d'ajouter 3, 5, 7, 9, 11 … c'est à dire un nombre impair, pour passer de l'un à l'autre. Nous écririons aujourd'hui $(n+1)^2 = n^2 + (2 n + 1)$. De la même façon, les Pythagoriciens créent la catégorie des nombres triangulaires : 1, 3, 6, 10, 15, 21 …
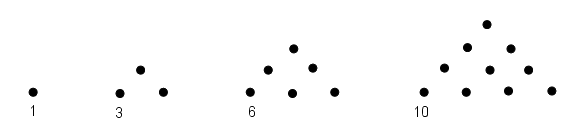
Cela ne correspond plus à des puissances mais à des nombres de la forme ${n \times (n+1) \over 2}$. On remarque également qu'il suffit d'ajouter 2, 3, 4, 5, 6, 7 … pour passer d'un nombre triangulaire au suivant. On obtient ainsi que $1 + 2 + 3 + 4 + ... + n = {n \times (n+1) \over 2}$.
Vous aurez peut-être reconnu dans la quatrième figure des nombres triangulaires, la fameuse Tétraktys que je vous présentais plus haut ? Ce nombre triangulaire était un symbole important sur lequel les Pythagoriciens prêtaient serment. Pourquoi était-il si important ? Car en additionnant le nombre de pièce de chaque étage du triangle on obtient 1+2+3+4=10, la décade, nombre symbolisant Dieu pour les pythagoriciens ! Cette classification peut être prolongée autant que voulu : nombres pentagonaux, hexagonaux, heptagonaux, octogonaux …
Nombres parfaits et amicaux
On doit également aux pythagoriciens l'étude des nombres parfaits ou amicaux ? Un nombre parfait est un nombre qui est égal à la somme de ses diviseurs propres (ses diviseurs sauf lui-même). Par exemple, le nombre 8 a comme diviseurs propres 1, 2 et 4. La somme donne 1+2+4=7. Donc 8 n'est pas un nombre parfait (mais on le dit tout de même presque parfait). En revanche, 6 n'a comme diviseurs propres que 1, 2 et 3 et 1+2+3=6. C'est donc un nombre parfait. Vous voulez d'autres nombres parfaits ? Cherchez-en par vous même. On n'en connaît que 48. Après 6, il n'y en a qu'un seul avant 100, puis un seul entre 100 et 1000, … Bon courage.
Les nombres amicaux reprennent ce principe mais en fonctionnant par paire. Chaque nombre est égal à la somme des diviseurs propres de l'autre. Par exemple : 220 et 284. Les diviseurs propres de 220 sont 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 et 110 ce qui donne une somme de 284. Les diviseurs propres de 284 sont 1, 2, 4, 71 et 142 ce qui donne une somme de 220. A priori, les pythagoriciens ne connaissaient que ces 2 nombres amicaux, le couple suivant étant 1184 et 1210.
Géométrie
Nous passerons rapidement les découvertes géométriques de Pythagore. Nous avons déjà parlé de la démonstration du théorème portant son nom, mais on lui doit également la démonstration de la toute aussi célèbre propriété " La somme des angles d'un triangle vaut 180° ".
Nous allons plutôt nous intéresser ici à une découverte majeure d'un élève de Pythagore : l'irrationnalité de $\sqrt 2$. Cet élève est Hippase de Métaponte et l'idée lui vint un jour d'employer le théorème de son maître dans un carré afin de déterminer la longueur de la diagonale.
Jusque là rien de bien étonnant. Nous avons déjà fait ce travail par nous même et avons montré que pour tout carré de côté a, la diagonale mesurait $a \times \sqrt 2$. D'ailleurs, ce résultat était déjà connu des Babyloniens, ainsi qu'en atteste une célèbre tablette d'argile répondant au doux nom de YBC 7289 (pour Yale Babylonian Collection, Yale étant une célèbre université américaine) :
Sur cette tablette (écrite dans un système sexagésimal, c'est à dire comportant 60 chiffres), il faut comprendre qu'un carré de côté 30 a une diagonale de longueur 42;25;35 (je ne fais pas la conversion dans notre système de numération) et que pour cela il suffit de multiplier par 1;24;51;10. Le nombre 1;24;51;10 est une approximation de $\sqrt 2$ exacte à 1 millionième près ! Une précision incroyable pour l'époque. Mais revenons à notre cher Hippase de Métaponte. Partant d'un problème déjà résolu depuis des millénaires, Hippase se demanda s'il ne pouvait trouver la valeur fractionnaire de $\sqrt 2$. Eh oui ! Vous savez bien que " Tout est nombre " pour Pythagore et ses disciples, toute longueur peut s'écrire comme un nombre entier ou fractionnaire (on disait alors que toute longueur était commensurable).
Voici, en langage moderne, sa réflexion. Supposons que l'on connaisse déjà deux nombres m et n tels que $\sqrt 2 = {m \over n}$. Supposons également que cette fraction soit irréductible. On peut alors en déduire que :
Il devient alors clair que le nombre m est un nombre pair. Nous pouvons donc l'écrire sous la forme $m = 2 \times p$. Remplaçons désormais m par cette nouvelle écriture dans la formule ci-dessus :
La dernière ligne nous indique donc que n est également un nombre pair. Oui mais nous avions supposé que la fraction $m \over n$ était irréductible, or nous venons de dire que m et n sont pairs ! La fraction n'est donc pas irréductible : nous aboutissons à une absurdité. Ce raisonnement par l'absurde venait de prouver de façon éclatante que $\sqrt 2$ n'était pas une fraction ! Nous dirions aujourd'hui que $\sqrt 2$ est un nombre irrationnel, on disait alors incommensurable.
Quelle fut la réaction de la fraternité ? Le dénis ! Cette découverte devint un tabou qu'il ne fallait révéler à personne. L'édifice de Pythagore semblait s'écrouler. Mais l'histoire ne s'arrête pas là : que faire du pauvre et Hippase ? Sur ce point, les récits divergent. Certains racontent qu'il aurait été banni, qu'il se serait suicidé ou que ses amis lui aurait construit un tombeau de son vivant (de quoi égayer les soirées 
). Mais ma version préférée est celle-ci : un jour, des membres de la confrérie proposèrent à Hippase de faire une petite virée en mer, ce que Hippase accepta. Une fois loin des côtés, ses "amis" se jetèrent sur lui, le ligotèrent et le jetèrent à l'eau. Quand Pythagore inaugure les méthodes de la mafia sicilienne. 
Astronomie
En Astronomie, les pythagoriciens vont apporter des idées neuves, révolutionnaires quoique fausses. L'univers pouvant et devant s'expliquer par les nombres et les figures géométriques, ils supposaient donc que la Terre, la Lune ou le Soleil étaient des sphères (la figure parfaite) et que leurs mouvements étaient parfaitement circulaires. Il sont donc les premiers à affirmer la sphéricité de la Terre et affirment également que la Terre tourne sur elle-même. Ils comprennent également que la Lune ne fait que refléter la lumière du Soleil.
Les pythagoriciens vont même plus loin en rejetant le système Géocentrique qui veut que Lune, Soleil, planètes et étoiles tournent autour de la Terre. Pour eux, c'est la Terre elle-même qui tourne autour d'un feu central. Mais attention ! Il ne s'agit pas d'un système Héliocentrique où le Soleil est au centre de toutes les rotations. Non, le soleil tourne lui aussi autour de ce feu central dont il réfléchit la lumière vers la Terre. Mais comme la Terre tourne sur elle-même, le feu central reste à jamais caché aux humains. Les pythagoriciens supposent également l'existence d'une anti-Terre, tournant elle aussi autour du feu central, mais diamétralement opposée à la Terre, donc inaccessible.
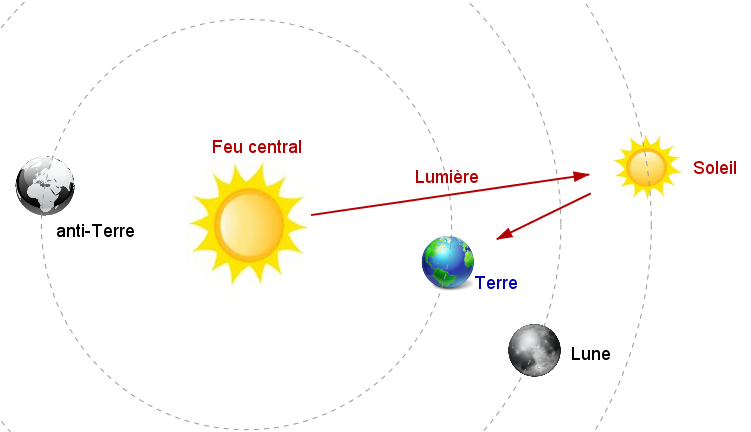
Si ce système, dit pyrocentrique, fait aujourd'hui sourire il n'en fut pas moins important de nombreux siècles plus tard. Car c'est lui qui inspira à Copernic l'idée du système héliocentrique. L'idée pythagoricienne de l'univers imposait de changer de paradigme : il fallait abandonner une Terre plate pour une Terre sphérique, abandonner sa place centrale dans l'univers pour une place quelconque autour d'un autre astre. Ce système fantaisiste n'en fut donc pas moins fondamental.
A retenir :
- Pythagore a découvert le lien entre fractions et notes de musique
- Les pythagoriciens étaient surtout des aficionados de l'arithmétique plus que de la géométrie
- La découverte que $\sqrt 2$ n'est pas une fraction fut un traumatisme pour les premiers pythagoriciens
- Les pythagoriciens sont les premiers à imaginer que la Terre est sphérique et qu'elle tourne à la fois sur elle-même et autour d'un foyer.