Ce premier chapitre va vous faire découvrir comment gérer des tensions analogiques avec votre carte Arduino. Vous allez d’abord prendre en main le fonctionnement d’un certain composant essentiel à la mise en forme d’un signal analogique, puis je vous expliquerai comment vous en servir avec votre Arduino. Rassurez-vous, il n’y a pas besoin de matériel supplémentaire pour ce chapitre !
- Un signal analogique : petits rappels
- Les convertisseurs analogiques –> numérique ou CAN
- Lecture analogique, on y vient…
- Exemple d’utilisation
- Une meilleure précision ?
Un signal analogique : petits rappels
Faisons un petit rappel sur ce que sont les signaux analogiques. D’abord, jusqu’à présent nous n’avons fait qu’utiliser des grandeurs numériques binaires. Autrement dit, nous n’avons utilisé que des états logiques HAUT et BAS. Ces deux niveaux correspondent respectivement aux tensions de 5V et 0V. Cependant, une valeur analogique ne se contentera pas d’être exprimée par 0 ou 1. Elle peut prendre une infinité de valeurs dans un intervalle donné. Dans notre cas, par exemple, la grandeur analogique pourra varier aisément de 0 à 5V en passant par 1.45V, 2V, 4.99V, etc. Voici un exemple de signal analogique, le très connu signal sinusoïdal :
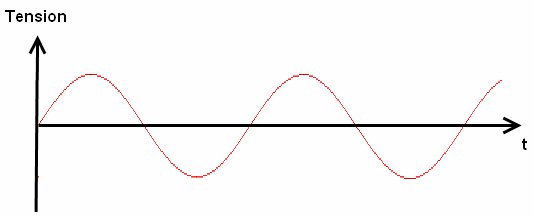
On retiendra que l’on ne s’occupe que de la tension et non du courant, en fonction du temps.
Si on essaye de mettre ce signal (ce que je vous déconseille de faire) sur une entrée numérique de l’Arduino et qu’on lit les valeurs avec digitalRead(), on ne lira que 0 ou 1. Les broches numériques de l’Arduino étant incapable de lire les valeurs d’un signal analogique.
Signal périodique
Dans la catégorie des signaux analogiques et même numériques (dans le cas d’horloge de signal pour le cadencement des micro-contrôleurs par exemple) on a les signaux dits périodiques. La période d’un signal est en fait un motif de ce signal qui se répète et qui donne ainsi la forme du signal. Prenons l’exemple d’un signal binaire qui prend un niveau logique 1 puis un 0, puis un 1, puis un 0, …
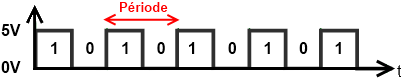
La période de ce signal est le motif qui se répète tant que le signal existe. Ici, c’est le niveau logique 1 et 0 qui forme le motif. Mais cela aurait pu être 1 1 et 0, ou bien 0 1 1, voir 0 0 0 1 1 1, les possibilités sont infinies ! Pour un signal analogique, il en va de même. Reprenons le signal de tout à l’heure :
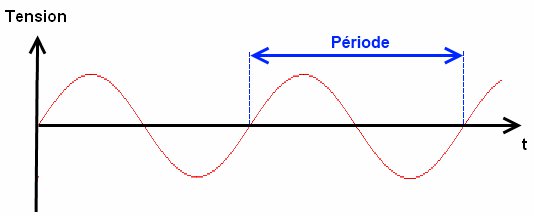
Ici le motif qui se répète est "la bosse de chameau" ou plus scientifiquement parlant : une période d’un signal sinusoïdal. Pour terminer, la période désigne aussi le temps que met un motif à se répéter. Si j’ai une période de 1ms, cela veut dire que le motif met 1ms pour se dessiner complètement avant de commencer le suivant. Et en sachant le nombre de fois que se répète le motif en 1 seconde, on peut calculer la fréquence du signal selon la formule suivante : ; avec F la fréquence, en hertz, du signal et T la période, en seconde, du signal.
Notre objectif
L’objectif va donc être double. Tout d’abord, nous allons devoir être capables de convertir cette valeur analogique en une valeur numérique, que l’on pourra ensuite manipuler à l’intérieur de notre programme. Par exemple, lorsque l’on mesurera une tension de 2,5V nous aurons dans notre programme une variable nommée "tension" qui prendra la valeur 250 lorsque l’on fera la conversion (ce n’est qu’un exemple). Ensuite, nous verrons avec Arduino ce que l’on peut faire avec les signaux analogiques. Je ne vous en dis pas plus…
Les convertisseurs analogiques –> numérique ou CAN
Qu’est-ce que c’est ?
C’est un dispositif qui va convertir des grandeurs analogiques en grandeurs numériques. La valeur numérique obtenue sera proportionnelle à la valeur analogique fournie en entrée, bien évidemment. Il existe différentes façons de convertir une grandeur analogique, plus ou moins faciles à mettre en œuvre, plus ou moins précises et plus ou moins onéreuses. Pour simplifier, je ne parlerai que des tensions analogiques dans ce chapitre.
La diversité
Je vais vous citer quelques types de convertisseurs, sachez cependant que nous n’en étudierons qu’un seul type.
- Convertisseur à simple rampe : ce convertisseur "fabrique" une tension qui varie proportionnellement en un cours laps de temps entre deux valeurs extrêmes. En même temps qu’il produit cette tension, il compte. Lorsque la tension d’entrée du convertisseur devient égale à la tension générée par ce dernier, alors le convertisseur arrête de compter. Et pour terminer, avec la valeur du compteur, il détermine la valeur de la grandeur d’entrée. Malgré sa bonne précision, sa conversion reste assez lente et dépend de la grandeur à mesurer. Il est, de ce fait, peu utilisé.
- Convertisseur flash : ce type de convertisseur génère lui aussi des tensions analogiques. Pour être précis, il en génère plusieurs, chacune ayant une valeur plus grande que la précédente (par exemple 2V, 2.1V, 2.2V, 2.3V, etc.) et compare la grandeur d’entrée à chacun de ces paliers de tension. Ainsi, il sait entre quelle et quelle valeur se trouve la tension mesurée. Ce n’est pas très précis comme mesure, mais il a l’avantage d’être rapide et malheureusement cher.
- Convertisseur à approximations successives : Pour terminer, c’est ce convertisseur que nous allons étudier…
Arduino dispose d’un CAN
Vous vous doutez bien que si je vous parle des CAN, c’est qu’il y a une raison. Votre carte Arduino dispose d’un tel dispositif intégré dans son cœur : le micro-contrôleur. Ce convertisseur est un convertisseur "à approximations successives". Je vais détailler un peu plus le fonctionnement de ce convertisseur par rapport aux autres dont je n’ai fait qu’un bref aperçu de leur fonctionnement (bien que suffisant).
Ceci rentre dans le cadre de votre culture générale électronique, ce n’est pas nécessaire de lire comment fonctionne ce type de convertisseur. Mais je vous recommande vivement de le faire, car il est toujours plus agréable de comprendre comment fonctionnent les outils qu’on utilise !
Principe de dichotomie
La dichotomie, ça vous parle ? Peut-être que le nom ne vous dit rien, mais il est sûr que vous en connaissez le fonctionnement. Peut-être alors connaissez-vous le jeu "plus ou moins en programmation ? Si oui alors vous allez pouvoir comprendre ce que je vais expliquer, sinon lisez le principe sur le lien que je viens de vous donner, cela vous aidera un peu. La dichotomie est donc une méthode de recherche conditionnelle qui s’applique lorsque l’on recherche une valeur comprise entre un minimum et un maximum. L’exemple du jeu "plus ou moins" est parfait pour vous expliquer le fonctionnement. Prenons deux joueurs. Le joueur 1 choisit un nombre compris entre deux valeurs extrêmes, par exemple 0 et 100. Le joueur 2 ne connait pas ce nombre et doit le trouver. La méthode la plus rapide pour que le joueur 2 puisse trouver quel est le nombre choisi par le joueur 1 est :
Joueur 1 dit : "quel est le nombre mystère ?"
> 40
Joueur 1 dit : "Ce nombre est plus grand"
> 80
Joueur 1 dit : "Ce nombre est plus petit"
> 60
Joueur 1 dit : "Ce nombre est plus grand"
> 70
Joueur 1 dit : "Ce nombre est plus grand"
> 75
Joueur 1 dit : "Ce nombre est plus petit"
> 72
Bravo, Joueur 2 a trouvé le nombre mystère !
Je le disais, le joueur 2, pour arriver le plus rapidement au résultat, doit choisir une méthode rapide. Cette méthode, vous l’aurez deviné, consiste à couper en deux l’espace de recherche. Au début, cet espace allait de 0 à 100, puis au deuxième essai de 40 à 100, au troisième essai de 40 à 80, etc.
Cet exemple n’est qu’à titre indicatif pour bien comprendre le concept.
En conclusion, cette méthode est vraiment simple, efficace et rapide ! Peut-être l’aurez-vous observé, on est pas obligé de couper l’espace de recherche en deux parties égales.
Le CAN à approximations successives
On y vient, je vais pouvoir vous expliquer comment il fonctionne. Voyez-vous le rapport avec le jeu précédent ? Pas encore ? Alors je m’explique. Prenons du concret avec une valeur de tension de 3.36V que l’on met à l’entrée d’un CAN à approximations successives (j’abrégerai par CAN dorénavant).
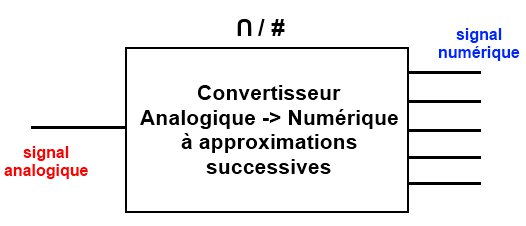
Notez le symbole du CAN qui se trouve juste au-dessus de l’image. Il s’agit d’un "U" renversé et du caractère #.
Cette tension analogique de 3.36V va rentrer dans le CAN et va ressortir sous forme numérique (avec des 0 et 1). Mais que se passe-t-il à l’intérieur pour arriver à un tel résultat ? Pour que vous puissiez comprendre correctement comment fonctionne ce type de CAN, je vais être obligé de vous apprendre plusieurs choses avant.
Le comparateur
Commençons par le comparateur. Comme son nom le laisse deviner, c’est quelque chose qui compare. Ce quelque chose est un composant électronique. Je ne rentrerai absolument pas dans le détail, je vais simplement vous montrer comment il fonctionne.
Comparer, oui, mais quoi ?
Des tensions ! Regardez son symbole, je vous explique ensuite…
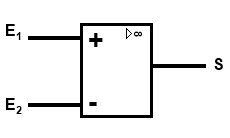
Vous observez qu’il dispose de deux entrées et et d’une sortie . Le principe est simple :
- Lorsque la tension alors ( étant la tension d’alimentation positive du comparateur)
- Lorsque la tension alors ( étant la tension d’alimentation négative, ou la masse, du comparateur)
- est une condition quasiment impossible, si tel est le cas (si on relie et ) le comparateur donnera un résultat faux
Parlons un peu de la tension d’alimentation du comparateur. Le meilleur des cas est de l’alimenter entre 0V et +5V. Comme cela, sa sortie sera soit égale à 0V, soit égale à +5V. Ainsi, on rentre dans le domaine des tensions acceptées par les micro-contrôleurs et de plus il verra soit un état logique BAS, soit un état logique HAUT. On peut réécrire les conditions précédemment énoncées comme ceci :
- alors
- alors
- , alors
Simple n’est-ce pas ?
Le démultiplexeur
Maintenant, je vais vous parler du démultiplexeur. C’est en fait un nom un peu barbare pour désigner un composant électronique qui fait de l’aiguillage de niveaux logiques (il en existe aussi qui font de l’aiguillage de tensions analogiques). Le principe est là encore très simple. Le démultiplexeur à plusieurs sorties, une entrée et des entrées de sélection :
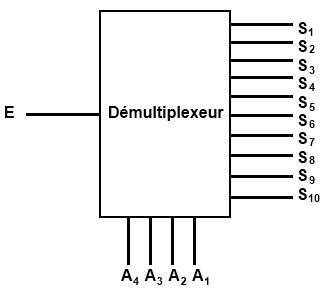
- est l’entrée où l’on impose un niveau logique 0 ou 1.
- Les sorties sont là où se retrouve le niveau logique d’entrée. UNE seule sortie peut être active à la fois et recopier le niveau logique d’entrée.
- Les entrées permettent de sélectionner quelle sera la sortie qui est active. La sélection se fait grâce aux combinaisons binaires. Par exemple, si je veux sélectionner la sortie 4, je vais écrire le code 0100 (qui correspond au chiffre décimal 4) sur les entrées à
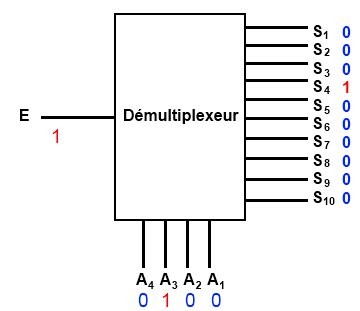
Je rappelle que, pour les entrées de sélection, le bit de poids fort est et le bit de poids faible . Idem pour les sorties, est le bit de poids faible et , le bit de poids fort.
La mémoire
Ce composant électronique sert simplement à stocker des données sous forme binaire.
Le convertisseur numérique analogique
Pour ce dernier composant avant l’acte final, il n’y a rien à savoir si ce n’est que c’est l’opposé du CAN. Il a donc plusieurs entrées et une seule sortie. Les entrées reçoivent des valeurs binaires et la sortie donne le résultat sous forme de tension.
Fonctionnement global
Rentrons dans les explications du fonctionnement d’un CAN à approximations successives. Je vous ai fait un petit schéma rassemblant les éléments précédemment présentés :
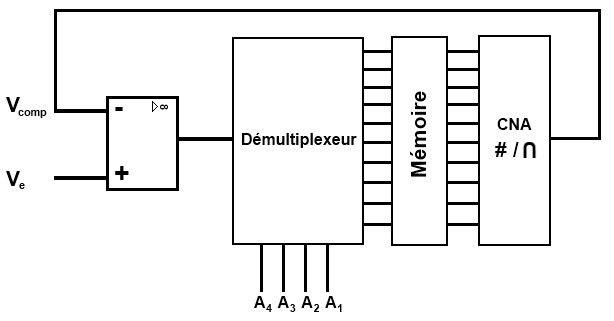
Voilà donc comment se compose le CAN. Si vous avez compris le fonctionnement de chacun des composants qui le constituent, alors vous n’aurez pas trop de mal à suivre mes explications. Dans le cas contraire, je vous recommande de relire ce qui précède et de bien comprendre et rechercher sur internet de plus amples informations si cela vous est nécessaire.
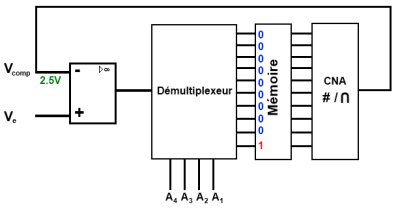
En premier lieu, commençons par les conditions initiales :
- est la tension analogique d’entrée, celle que l’on veut mesurer en la convertissant en signal numérique.
- La mémoire contient pour l’instant que des 0 sauf pour le bit de poids fort () qui est à 1. Ainsi, le convertisseur numérique analogique va convertir ce nombre binaire en une tension analogique qui aura pour valeur 2.5V.
- Pour l’instant, le démultiplexeur n’entre pas en jeu.
Suivons le fonctionnement étape par étape :
Étape 1 :
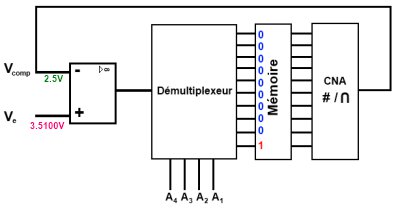
- J’applique une tension précisément.
- Le comparateur compare la tension à la tension . Étant donné que , on a un Niveau Logique 1 en sortie du comparateur.
- Le multiplexeur entre alors en jeux. Avec ses signaux de sélections, il va sélectionner la sortie ayant le poids le plus élevé, soit .
- La mémoire va alors enregistrer le niveau logique présent sur la broche , dans notre cas c’est 1.
Étape 2 :
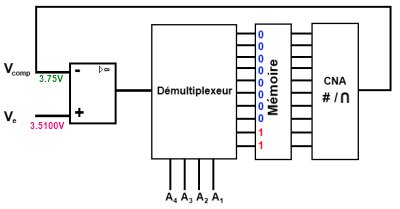
- Au niveau de la mémoire, on change le deuxième bit de poids fort (mais moins fort que le premier) correspondant à la broche en le passant à 1.
- En sortie du CNA, on aura alors une tension de
- Le comparateur compare, il voit donc il donne un état logique 0.
- La mémoire enregistre alors le niveau sur la broche qui est à 0.
Étape 3 :
Redondante aux précédentes
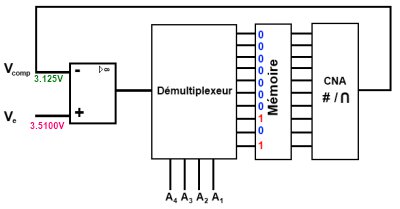
- On passe le troisième bit le plus fort (broche ) à 1.
- Le CNA converti le nombre binaire résultant en une tension de .
- Le comparateur voit , sa sortie passe à 1.
- La mémoire enregistre l’état logique de la broche qui est à 1.
Le CAN continue de cette manière pour arriver au dernier bit (celui de poids faible). En mémoire, à la fin de la conversion, se trouve le résultat. On va alors lire cette valeur binaire que l’on convertira ensuite pour l’exploiter. Bon, j’ai continué les calculs à la main (n’ayant pas de simulateur pour le faire à ma place), voici le tableau des valeurs :
| Poids du bit | NL en sortie du comparateur | Bits stockés en mémoire | Tension en sortie du convertisseur CNA (en V) |
|---|---|---|---|
| 10 | 1 | 1 | 2.5 |
| 9 | 0 | 0 | 3.75 |
| 8 | 1 | 1 | 3.125 |
| 7 | 1 | 1 | 3.4375 |
| 6 | 0 | 0 | 3.59375 |
| 5 | 0 | 0 | 3.515625 |
| 4 | 1 | 1 | 3.4765625 |
| 3 | 1 | 1 | 3.49609375 |
| 2 | 1 | 1 | 3.505859375 |
| 1 | 0 | 0 | 3.5107421875 |
Résultat : Le résultat de la conversion donne :
| Résultat de conversion (binaire) | Résultat de conversion (décimale) | Résultat de conversion (Volts) |
|---|---|---|
| 1011001110 | 718 | 3,505859375 |
Observez la précision du convertisseur. Vous voyez que la conversion donne un résultat (très) proche de la tension réelle, mais elle n’est pas exactement égale. Ceci est dû au pas du convertisseur.
Pas de calcul du CAN
Qu’est-ce que le pas de calcul ? Eh bien il s’agit de la tension minimale que le convertisseur puisse "voir". Si je mets le bit de poids le plus faible à 1, quelle sera la valeur de la tension ? Le convertisseur a une tension de référence de 5V. Son nombre de bit est de 10. Donc il peut "lire" : valeurs pour une seule tension. Ainsi, sa précision sera de : La formule à retenir sera donc :
$$ \frac{V_{ref}}{2^N} $$
Avec :
- : tension de référence du convertisseur
- : nombre de bit du convertisseur
Il faut donc retenir que, pour ce convertisseur, sa précision est de . Donc, si on lui met une tension de par exemple sur son entrée, le convertisseur sera incapable de la voir et donnera un résultat égal à 0V.
Les inconvénients
Pour terminer avant de passer à l’utilisation du CNA avec Arduino, je vais vous parler de ses inconvénients. Il en existe trois principaux :
- la plage de tension d’entrée : le convertisseur analogique de l’Arduino ne peut recevoir à son entrée que des tensions comprises entre 0V et +5V. On verra plus loin comment améliorer la précision du CAN.
- la précision : la précision du convertisseur est très bonne sauf pour les deux derniers bits de poids faible. On dit alors que la précision est de (à cause du pas de calcul que je viens de vous expliquer).
- la vitesse de conversion : le convertisseur N/A de la carte Arduino n’a pas une très grande vitesse de conversion par rapport à un signal audio par exemple. Ainsi , si l’on convertit un signal audio analogique en numérique grâce à la carte Arduino, on ne pourra entendre que les fréquences en dessous de 10kHz. Dans bien des cas cela peut être suffisant, mais d’en d’autre il faudra utiliser un convertisseur A/N externe (un composant en plus) qui sera plus rapide afin d’obtenir le spectre audio complet d’un signal sonore.
Lecture analogique, on y vient…
Lire la tension sur une broche analogique
Un truc très sympa avec Arduino, c’est que c’est facile à prendre en main. Et ça se voit une fois de plus avec l’utilisation des convertisseurs numérique -> analogique ! En effet, vous n’avez qu’une seule nouvelle fonction à retenir : analogRead() !
analogRead(pin)
Cette fonction va nous permettre de lire la valeur lue sur une entrée analogique de l’Arduino. Elle prend un argument et retourne la valeur lue :
- L’argument est le numéro de l’entrée analogique à lire (explication ci-dessous)
- La valeur retournée (un
int) sera le résultat de la conversion analogique- >numérique
Sur une carte Arduino Uno, on retrouve 6 CAN. Ils se trouvent tous du même côté de la carte, là où est écrit "Analog IN" :

Ces 6 entrées analogiques sont numérotées, tout comme les entrées/sorties logiques. Par exemple, pour aller lire la valeur en sortie d’un capteur branché sur le convertisseur de la broche analogique numéro 3, on fera : valeur = analogRead(3);.
Ne confondez pas les entrées analogiques et les entrées numériques ! Elles ont en effet le même numéro pour certaines, mais selon comment on les utilise, la carte Arduino saura si la broche est analogique ou non.
Mais comme nous sommes des programmeurs intelligents et organisés, on nommera les variables proprement pour bien travailler de la manière suivante :
// broche analogique 3 OU broche numérique 3
const int monCapteur = 3;
// la valeur lue sera comprise entre 0 et 1023
int valeurLue = 0;
// fonction setup()
{
}
void loop()
{
// on mesure la tension du capteur sur la broche analogique 3
valeurLue = analogRead(monCapteur);
// du code et encore du code ...
}
Convertir la valeur lue
Bon c’est bien, on a une valeur retournée par la fonction comprise entre 0 et 1023, mais ça ne nous donne pas vraiment une tension ça ! Il va être temps de faire un peu de code (et de math) pour convertir cette valeur… Et si vous réfléchissiez un tout petit peu pour trouver la solution sans moi ? … Trouvée ?
Conversion
Comme je suis super sympa je vais vous donner la réponse, avec en prime : une explication ! Récapitulons. Nous avons une valeur entre 0 et 1023. Cette valeur est l’image de la tension mesurée, elle-même comprise entre 0V et +5V. Nous avons ensuite déterminé que le pas du convertisseur était de 4.88mV par unité. Donc, deux méthodes sont disponibles :
- avec un simple produit en croix
- en utilisant le pas calculé plus tôt
Exemple : La mesure nous retourne une valeur de 458.
- Avec un produit en croix on obtient : ;
- En utilisant le pas calculé plus haut on obtient : .
Les deux méthodes sont valides, et donnent les mêmes résultats. La première à l’avantage de faire ressortir l’aspect "physique" des choses en utilisant les tensions et la résolution du convertisseur.
Voici une façon de le traduire en code :
// variable stockant la valeur lue sur le CAN
int valeurLue;
// résultat stockant la conversion de valeurLue en Volts
float tension;
void loop()
{
valeurLue = analogRead(uneBrocheAvecUnCapteur);
// produit en croix, ATTENTION, donne un résultat en mV !
tension = valeurLue * 4.88;
// formule à aspect "physique", donne un résultat en V !
tension = valeurLue * (5 / 1023);
}
Mais il n’existe pas une méthode plus "automatique" que faire ce produit en croix ?
Eh bien SI ! En effet, l’équipe Arduino a prévu que vous aimeriez faire des conversions facilement et donc une fonction est présente dans l’environnement Arduino afin de vous faciliter la tâche ! Cette fonction se nomme map(). À partir d’une valeur d’entrée, d’un intervalle d’entrée et d’un intervalle de sortie, la fonction vous retourne la valeur équivalente comprise entre le deuxième intervalle. Voici son prototype de manière plus explicite :
sortie = map(valeur_d_entree,
valeur_extreme_basse_d_entree,
valeur_extreme_haute_d_entree,
valeur_extreme_basse_de_sortie,
valeur_extreme_haute_de_sortie
);
// cette fonction retourne la valeur calculée équivalente
// entre les deux intervalles de sortie
mapPrenons notre exemple précédent. La valeur lue se nomme "valeurLue". L’intervalle d’entrée est la gamme de la conversion allant de 0 à 1023. La gamme (ou intervalle) de "sortie" sera la tension réelle à l’entrée du micro-contrôleur, donc entre 0 et 5V. En utilisant cette fonction nous écrirons donc :
// conversion de la valeur lue en tension en mV
tension = map(valeurLue, 0, 1023, 0, 5000);
mapPourquoi tu utilises 5000mV au lieu de mettre simplement 5V ?
Pour la simple et bonne raison que la fonction map utilise des entiers. Si j’utilisais 5V au lieu de 5000mV j’aurais donc seulement 6 valeurs possibles pour ma tension (0, 1, 2, 3, 4 et 5V). Pour terminer le calcul, il sera donc judicieux de rajouter une dernière ligne :
// conversion de la valeur lue en tension en mV
tension = map(valeurLue, 0, 1023, 0, 5000);
// conversion des mV en V
tension = tension / 1000;
Au retour de la liaison série (seulement si on envoie les valeurs par la liaison série) on aurait donc (valeurs à titre d’exemple) :
valeurLue = 458
tension = 2.290V
On est moins précis que la tension calculée plus haut, mais on peut jouer en précision en modifiant les valeurs de sortie de la fonction map(). Ou bien garder le calcul théorique et le placer dans une "fonction maison".
Exemple d’utilisation
Le potentiomètre
Qu’est-ce que c’est que cette bête-là encore ?
Le potentiomètre (ou "potar" pour les (très) intimes) est un composant très fréquemment employé en électronique. On le retrouve aussi sous le nom de résistance variable. Comme ce dernier nom l’indique si bien, un potentiomètre nous permet entre autres de réaliser une résistance variable. En effet, on retrouve deux applications principales que je vais vous présenter juste après. Avant toute chose, voici le symbole du potentiomètre :
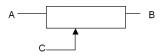
Cas n°1 : le pont diviseur de tension
On y remarque une première chose importante, le potentiomètre a trois broches. Deux servent à borner les tensions maximum (A) et minimum (B) que l’on peut obtenir à ses bornes, et la troisième © est reliée à un curseur mobile qui donne la tension variable obtenue entre les bornes précédemment fixées. Ainsi, on peut représenter notre premier cas d’utilisation comme un "diviseur de tension réglable". En effet, lorsque vous déplacez le curseur, en interne cela équivaut à modifier le point milieu. En termes électroniques, vous pouvez imaginer avoir deux résistances en série (R1 et R2 pour être original). Lorsque vous déplacez votre curseur vers la borne basse, R1 augmente alors que R2 diminue et lorsque vous déplacez votre curseur vers la borne haute, R2 augmente alors que R1 diminue. Voici un tableau montrant quelques cas de figure de manière schématique :
| Schéma équivalent | Position du curseur | Tension sur la broche C |
|---|---|---|
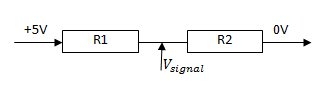 |
Curseur à la moitié | |
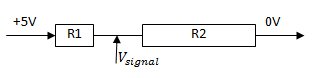 |
Curseur à 25% du départ | |
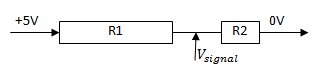 |
Curseur à 75% du départ |
Si vous souhaitez avoir plus d’informations sur les résistances et leurs associations ainsi que sur les potentiomètres, je vous conseille d’aller jeter un œil sur ce chapitre.
Cas n°2 : la résistance variable
Le deuxième cas d’utilisation du potentiomètre est la résistance variable. Cette configuration est très simple, il suffit d’utiliser le potentiomètre comme une simple résistance dont les bornes sont A et C ou B et C. On pourra alors faire varier la valeur ohmique de la résistance grâce à l’axe du potentiomètre.
Attention, il existe des potentiomètres linéaires (la valeur de la tension évolue de manière proportionnelle au déplacement du curseur), mais aussi des potentiomètres logarithmique/anti-logarithmique (la valeur de la tension évolue de manière logarithmique ou anti-logarithmique par rapport à la position du curseur). Choisissez-en dont un qui est linéaire si vous souhaitez avoir une proportionnalité.
Utilisation avec Arduino
Vous allez voir que l’utilisation avec Arduino n’est pas vraiment compliquée. Il va nous suffire de raccorder les alimentations sur les bornes extrêmes du potentiomètre, puis de relier la broche du milieu sur une entrée analogique de la carte Arduino :
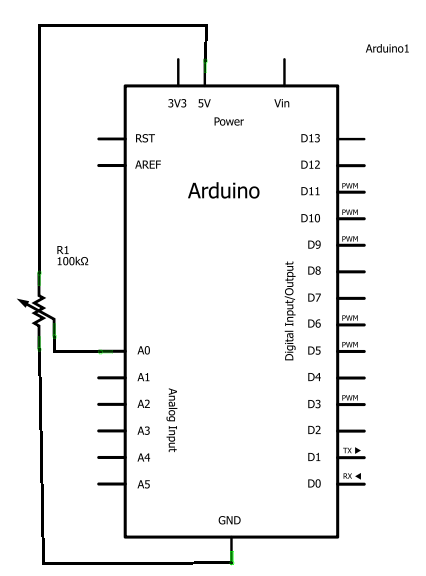
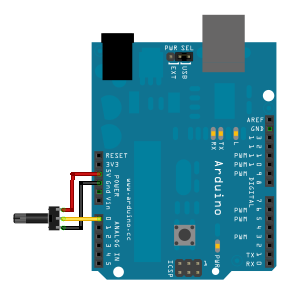
Une fois le raccordement fait, nous allons faire un petit programme pour tester cela. Ce programme va simplement effectuer une mesure de la tension obtenue sur le potentiomètre, puis envoyer la valeur lue sur la liaison série (ça nous fera réviser ). Dans l’ordre, voici les choses à faire :
- Déclarer la broche analogique utilisée (pour faire du code propre
- Mesurer la valeur
- L’afficher !
Je vous laisse chercher ? Aller, au boulot ! … Voici la correction, c’est le programme que j’ai fait, peut-être que le vôtre sera mieux :
// le potentiomètre, branché sur la broche analogique 0
const int potar = 0;
// variable pour stocker la valeur lue après conversion
int valeurLue;
// on convertit cette valeur en une tension
float tension;
void setup()
{
// on se contente de démarrer la liaison série
Serial.begin(9600);
}
void loop()
{
// on convertit en nombre binaire la tension lue en sortie du potentiomètre
valeurLue = analogRead(potar);
// on traduit la valeur brute en tension (produit en croix)
tension = valeurLue * 5.0 / 1023;
// on affiche la valeur lue sur la liaison série
Serial.print("valeurLue = ");
Serial.println(valeurLue);
// on affiche la tension calculée
Serial.print("Tension = ");
Serial.print(tension,2);
Serial.println(" V");
// on saute une ligne entre deux affichages
Serial.println();
// on attend une demi-seconde pour que l'affichage ne soit pas trop rapide
delay(500);
}
Vous venez de créer votre premier voltmètre !
Simulation équivalente :
!(https://www.tinkercad.com/embed/krCu0Cc8OmC)
Une meilleure précision ?
Est-il possible d’améliorer la précision du convertisseur ?
Voilà une question intéressante à laquelle je répondrai qu’il existe deux solutions plus ou moins faciles à mettre en œuvre.
Solution 1 : modifier la plage d’entrée du convertisseur
C’est la solution la plus simple ! Voyons deux choses…
Tension de référence interne
Le micro-contrôleur de l’Arduino possède plusieurs tensions de référence utilisables selon la plage de variation de la tension que l’on veut mesurer. Prenons une tension, en sortie d’un capteur, qui variera entre 0V et 1V et jamais au delà. Par défaut, la mesure se fera entre 0 et 5V sur 1024 niveaux (soit une précision de 4.88 mV). Ce qui veut dire qu’on aura seulement les 204 premiers niveaux d’utiles puisque tout le reste correspondra à plus d’un volt. Pour améliorer la précision de lecture, on va réduire la plage de mesure d’entrée du convertisseur analogique - > numérique en réduisant la tension de référence utilisée (initialement 5V). Pour cela, rien de matériel, tout se passe au niveau du programme puisqu’il y a une fonction qui existe : analogReference(). Cette fonction prend en paramètre le nom de la référence à utiliser :
- DEFAULT : La référence de 5V par défaut (ou 3,3V pour les cartes Arduino fonctionnant sous cette tension, telle la Due)
- INTERNAL : Une référence interne de 1.1V (pour la Arduino Uno)
- INTERNAL1V1 : Comme ci-dessus mais pour la Arduino Mega
- INTERNAL2V56 : Une référence de 2.56V (uniquement pour la Mega)
- EXTERNAL : La référence sera celle appliquée sur la broche ARef
Dans notre cas, le plus intéressant sera de prendre la valeur INTERNAL pour pouvoir faire des mesures entre 0 et 1.1V. Ainsi, on aura 1024 niveaux ce qui nous fera une précision de 1.07mV. C’est bien meilleur ! Le code est à placer dans la fonction setup() de votre programme :
void setup()
{
// permet de choisir une tension de référence de 1.1V
analogReference(INTERNAL);
}
Tension de référence externe
Maintenant que se passe t’il si notre mesure devait être faite entre 0 et 3V ? On ne pourrait plus utiliser INTERNA1V1 puisqu’on dépasse les 1.1V. On risquerais alors de griller le comparateur. Dans le cas d’une Arduino Mega, on ne peut pas non plus utiliser INTERNAL2V56 puisqu’on dépasse les 2.56V. Nous allons donc ruser en prenant une référence externe à l’aide de la valeur EXTERNAL comme ceci :
void setup()
{
// permet de choisir une tension de référence externe à la carte
analogReference(EXTERNAL);
}
Ensuite, il ne restera plus qu’à apporter une tension de référence supérieur à 3V sur la broche ARef de la carte pour obtenir notre nouvelle référence.
Astuce : la carte Arduino produit une tension de 3.3V (à côté de la tension 5V). Vous pouvez donc utiliser cette tension directement pour la tension de référence du convertisseur. Il suffit pour cela de relier avec un fil la sortie indiquée 3.3V à l’entrée AREF.
Attention cependant, la tension maximale de référence ne peut être supérieure à +5V et la minimale inférieure à 0V. En revanche, toutes les tensions comprises entre ces deux valeurs sont acceptables.
Mais, si je veux que ma tension d’entrée puisse varier au-delà de +5V, comment je fais ? Y a-t-il un moyen d’y parvenir ?
Oui, voyez ce qui suit…
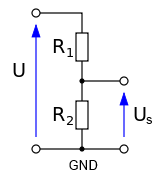
Solution 2 : utiliser un pont diviseur de tension
Nous avons vu cela à la partie précédente avec le potentiomètre. Il s’agit en fait de diviser votre signal par un certain ratio afin de l’adapter aux contraintes d’entrées du convertisseur. Par exemple, imaginons que nous ayons une mesure à faire sur un appareil qui délivre une tension comprise entre 0 et 10V. Cela ne nous arrange pas puisque nous ne sommes capable de lire des valeurs qu’entre 0 et 5V. Nous allons donc diviser cette mesure par deux afin de pouvoir la lire sans risque. Pour cela, on utilisera deux résistances de valeur identique (2 fois par exemple) pour faire un pont diviseur de tension. La tension à mesurer rentre dans le pont ( sur le schéma ci-contre) et la tension mesurable sort au milieu du pont (tension ). Il ne reste plus qu’à connecter la sortie du pont à une entrée analogique de la carte Arduino et lire la valeur de la tension de sortie.
Libre à vous de modifier les valeurs des résistances du pont diviseur de tension pour faire rentrer des tensions différentes (même au delà de 10V !). Attention cependant à ne pas dépasser les +5V en sortie du pont !
Solution 3 : utiliser un CAN externe
La deuxième solution consisterait simplement en l’utilisation d’un convertisseur analogique -> numérique externe. A vous de choisir le bon. Il en existe beaucoup, ce qu’il faut principalement regarder c’est :
- la précision (10 bits pour Arduino, existe d’autre en 12bits, 16bits, …)
- la vitesse d’acquisition (celui d’Arduino est à une vitesse de 100µs)
- le mode de transfert de la lecture (liaison série, I²C, …)
- le nombre d’entrées (6 sur Arduino Uno)
- la tension d’entrée maximale et minimale (max +5V et min 0V)
Solution 4 : Modifier la fréquence de fonctionnement de l’ADC
Cette solution et ses limites sont illustrées dans ce billet de Titi_Alone. C’est une manipulation un peu plus avancée qui fera appel à la manipulation de registres internes au microcontrôleur de l’Arduino. Les paramètres de base devraient cependant convenir à la majorité de vos applications.
Au programme :
- Le prochain chapitre est un TP faisant usage de ces voies analogiques
- Le chapitre qui le suit est un chapitre qui vous permettra de créer des tensions analogiques avec votre carte Arduino, idéal pour mettre en œuvre la deuxième solution d’amélioration de la précision de lecteur du convertisseur !
En somme, ce chapitre vous a permis de vous familiariser un peu avec les tensions analogiques, ce qui vous permettra par la suite de gérer plus facilement les grandeurs renvoyées par des capteurs quelconques.