Il n’y a aucune raison de nous arrêter en si bon chemin. Nous avons commencé avec une inconnue, puis deux, alors pourquoi pas trois, quatre, cinq ou six ?
Dans ce chapitre, nous allons voir les principes généraux qui permettent de trouver les solutions d’équations à plusieurs inconnues. Mais si les méthodes de résolution sont intéressantes, il devient souvent très long et fastidieux d’entrer dans les calculs à mesure que le nombre d’inconnues augmente. Heureusement, nous avons aujourd’hui des ordinateurs capables de faire ces calculs à notre place.
Représentation des solutions
Les inconnues
Si on augmente le nombre d’inconnues, il faut également augmenter le nombre de lettres pour les désigner.
Si on a trois inconnues, le choix reste simple : , et . Mais dès lors que l’on arrive à quatre inconnues ou plus, il n’y a pas moyen de poursuivre l’alphabet. On pourrait tout à fait décider de revenir en arrière et prendre des lettres comme , ou pour les quatrième, cinquième et sixième inconnues, mais cette méthode ne marcherait plus si on dépassait la vingt-sixième. En fait, la façon la plus courante de noter les inconnues dès qu’elles sont au moins quatre consiste à utiliser la lettre avec des indices. Ainsi, si on a cinq inconnues, on les notera de la façon suivante :
Voici par exemple une équation du second degré à cinq inconnues :
Dans d’autres dimensions
En 3D
Nous avons vu dans le chapitre précédent que les solutions d’une équation à deux inconnues peuvent se représenter dans un plan. En utilisant le même procédé, il est possible de représenter les solution d’une équation à trois inconnues dans l’espace en trois dimensions.
Regardons par exemple l’équation suivante :
On peut constater que les valeurs , et sont une solution de cette équation. Cette solution peut être représentée dans l’espace par le point de coordonnées :

Et si on continuait à chercher les solutions de cette équation pour les placer toutes dans le repère, on verrait peu à peu se dessiner la figure suivante :

C’est beau, n’est-ce pas ? Cette figure porte le doux nom de cylindre parabolique.
Seul un petit morceau de la figure est représenté dans l’image ci-dessus. Le cylindre parabolique entier se prolonge à l’infini.
Et au delà
Si vous avez compris le principe vous devez vous douter de ce qui suit : les solutions d’une équation à quatre inconnues peuvent se représenter dans un espace en quatre dimensions. Et d’une manière générale, s’il y a inconnues, les solutions se représentent dans un espace à dimensions.
Quoi ? Quoi ? Quoi ? Qu’est-ce que c’est que ça, la quatrième dimension ? Il est possible d’aller au dessus de trois dimensions ?
En mathématiques, oui ! Au delà de la dimension trois, les espaces ne peuvent plus être représentés facilement car notre monde physique est en 3D, mais rien n’empêche de les considérer de façon abstraite. Un espace de dimension 4 est un espace dans lequel chaque point est repéré par 4 coordonnées, tout simplement.
Équations du premier degré
Trois inconnues
En dimension 3, une équation du premier degré s’écrit de la façon suivante :
Et de la même façon que les équations à deux inconnues se représentent par une droite, celles à trois inconnues se représentent par un plan.
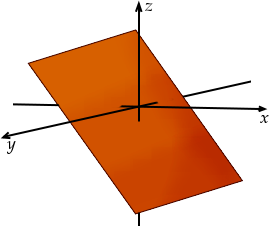
Si on considère un système de deux équations, alors les solutions se trouvent à l’intersection de deux plans. Or l’intersection de deux plans quelconques, c’est une droite.
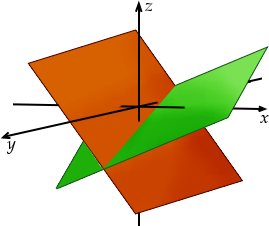
Et si on ajoute une nouvelle équation pour avoir un système de trois équations à trois inconnues, alors on cherche l’intersection de trois plans. Cette fois, il n’y a plus qu’un point, c’est-à-dire une unique solution.
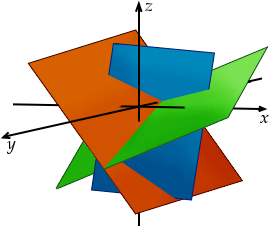
Ce que nous venons de dire n’est vrai que si les trois plans sont disposés de manière quelconque dans l’espace. Il existe des cas particuliers, comme par exemple si deux plans sont parallèles, où il n’y a aucune solution car deux plans parallèles n’ont pas d’intersection.
Un autre cas particulier que l’on peut rencontrer est par exemple celui de ce système :
Ce qu’il faut remarquer ici, c’est que la troisième équation est la somme des deux premières. Ainsi, si les deux premières équations sont vérifiées, alors la troisième le sera automatiquement. Cette dernière n’apporte donc aucune information supplémentaire sur les inconnues et du coup, c’est un peu comme si nous n’avions que deux équations.
Géométriquement, cela se traduit par le fait que les trois plans passent tous par la même droite. Ainsi, l’ensemble des solutions est une droite.
À plus de quatre
À partir de quatre, comme les inconnues sont numérotées par un indice, nous allons faire la même chose avec leurs coefficients. Ainsi une équation du premier degré à cinq inconnues se notera de la façon suivante :
Et d’une manière générale, en voici une avec un nombre quelconque d’inconnues :
Si vous connaissez l’utilisation du signe pour les sommes, cette équation peut s’écrire ainsi :
La règle est alors la suivante :
Dans un espace de dimension , l’ensemble des solutions d’une équation de premier degré à inconnues est un espace de dimension .
Remarquez que cela marche bien pour les trois premières dimensions que nous avons vues :
- Si , il y a une inconnue et une seule solution qui se représente par un point (dimension 0).
- Si , il y a deux inconnues et les solutions forment une droite (dimension 1).
- Si , il y a trois inconnues et les solutions forment un plan (dimension 2).
Dans un espace quelconque, un espace ayant juste une dimension de moins s’appelle un hyperplan. Ainsi, en dimension 1 un hyperplan est un point, en dimension 2 c’est une droite et en dimension 3 c’est un plan.
Les choses fonctionnent alors exactement de la même façon que pour la dimension 3 :
- si on a une seule équation, alors les solutions sont représentées par un hyperplan, c’est-à-dire de dimension ;
- si on a un système de deux équations, alors l’intersection de deux hyperplans donne un espace de dimension ;
- si on a un système de trois équations, alors l’intersection de trois hyperplans donne un espace de dimension ;
- si on a un système de quatre équations, alors l’intersection de quatre hyperplans donne un espace de dimension …
Et ainsi de suite. À chaque fois qu’on ajoute une équation, on ajoute une contrainte supplémentaire sur les solutions ce qui leur fait perdre une dimension.
Par exemple, si on étudie un système de 300 équations à 1000 inconnues, alors l’ensemble des solutions sera un espace de dimension 700 ! S’il y a 999 équations pour 1000 inconnues, on a une droite. Et pour qu’il n’y ait qu’une solution, il faut qu’il y ait autant d’équations que d’inconnues.
Attention, ces règles sont vraies quand il n’y a pas de cas particuliers comme ceux que nous avons déjà vus : hyperplans parallèles qui n’ont pas d’intersection ou encore équations qui ne sont pas indépendantes les unes des autres. Il existe des méthodes d’algèbre linéaire permettant de détecter ces cas particuliers quand ils se présentent, mais nous ne les verrons pas car elles sont un peu trop compliquées pour le niveau de ce cours.
Méthodes de résolution
Bon, il y a bien un moment où il faut mettre les mains dans le cambouis, c’est-à-dire apprendre concrètement à faire les calculs : c’est maintenant. Dans cette section, nous allons voir deux méthodes de résolution des systèmes d’équations. Pour les expliquer, nous allons prendre pour exemple le système suivant :
Il s’agit d’un système du premier degré à trois inconnues. Vous allez voir que les méthodes que nous allons utiliser peuvent également s’appliquer s’il y a plus d’inconnues ou quand les équations ne sont pas du premier degré. Mais bien entendu, plus on complique, plus les calculs sont longs et pénibles. Ce système va déjà nous donner un peu de fil à retordre.
Par substitution
Nous allons commencer par prendre la première équation et la résoudre avec l’inconnue comme si et étaient des nombres connus. C’est assez facile, on trouve ceci :
Maintenant que nous avons cette valeur de en fonction de et , nous allons la substituer dans les deux autres équations (d’où le nom de la méthode). On trouve ceci :
Ce qui se simplifie en regroupant les y et les z de la façon suivante :
À ce stade, nous sommes passé d’un système de trois équations à trois inconnues à un système de deux équations à deux inconnues. On peut maintenant répéter le processus avec y pour éliminer une nouvelle inconnue. La première équation de notre nouveau système nous donne :
On reporte ça dans la dernière équation et on trouve :
Nous n’avons désormais plus qu’une inconnue, donc nous savons comment faire :
Nous venons de trouver , il suffit maintenant de remonter tout ça pour retrouver et :
et
Au bout du compte, nous trouvons qu’il n’y a bien qu’une seule solution qui est la suivante :
Ce n’était pas si dur que ça finalement.
Par élimination
La méthode par élimination est assez proche de la précédente, mais elle se présente un peu différemment. Elle est basée sur le principe suivant : on ne change pas les solutions d’un système d’équations si on ajoute ou soustrait une des équations du système à une autre.
Pour bien comprendre, reprenons notre système de départ.
Alors, il est possible par exemple de soustraire la première équation à la deuxième. On trouve ceci :
Bien sûr, le système n’est plus le même puisque la deuxième équation a été modifiée, mais ce qui compte, c’est que ses solutions sont toujours les mêmes.
Ce procédé peut être un peu subtil à comprendre la première fois qu’on le voit. Puisque les solutions que nous cherchons doivent vérifier la première équation, cela signifie que nous avons ajouté 0 à la deuxième équation ! En définitive, nous avons bien changé les solutions de la deuxième équation, mais nous n’avons pas changé les solutions qui vérifient à la fois la première et la deuxième équation. Notre nouveau système a donc les mêmes solutions que le système de départ.
Cette manipulation simplifie la solution, car vous aurez constaté qu’au passage, nous avons éliminé l’inconnue x de la deuxième équation (d’où le nom de la méthode par élimination ).
Il ne nous reste plus qu’à continuer. Pour éliminer les x de la troisième équation, nous allons lui soustraire deux fois la première. On trouve alors ceci :
Nous pouvons maintenant éliminer le y de la troisième ligne en lui retranchant deux fois la deuxième :
Ça simplifie pas mal les choses, vous ne trouvez pas ? Maintenant regardez la troisième équation : il n’y a plus que l’inconnue , nous savons donc la résoudre et nous trouvons :
Maintenant, nous pouvons remplacer z par sa valeur dans les deux autres équations :
Et nous pouvons maintenant résoudre la deuxième équation. On trouve et on peut reporter ce résultat dans la première équation qui à son tour n’a plus qu’une inconnue :
Il n’y a plus qu’à achever la première équation :
Et c’est gagné ! On trouve bien heureusement la même solution qu’avec la méthode de substitution. Vous voyez que finalement, une fois que l’on a éliminé suffisamment d’inconnues dans plusieurs équations, toutes les équations tombent les unes après les autres comme des dominos.
Quand on l’applique à un système du premier degré, cette méthode s’appelle également la méthode d’élimination de Gauss-Jordan ou méthode du pivot de Gauss.