Cette partie est plus formelle que ce nous avons vu jusqu’à maintenant. Si le lecteur souhaite se concentrer sur l’utilisation de l’outil, l’introduction de ce chapitre et les deux premières sections (sur les instructions de base et « le bonus stage ») sont dispensables. Si ce que nous avons présenté jusqu’à maintenant a semblé ardu au lecteur sur un plan formel, il est également possible de réserver l’introduction et ces deux sections pour une deuxième lecture.
Les sections sur les boucles sont en revanches indispensables. Les éléments plus formels de ces sections seront signalés.
Pour chaque notion en programmation C, nous associerons la règle d’inférence qui lui correspond, la règle utilisée de calcul de plus faible préconditions qui la régit, et des exemples d’utilisation. Pas forcément dans cet ordre et avec plus ou moins de liaison avec l’outil. Les premiers points seront plus focalisés sur la théorie que sur l’utilisation car ce sont les plus simples, au fur et à mesure, nous nous concentrerons de plus en plus sur l’outil, en particulier quand nous attaquerons le point concernant les boucles.
Règle d’inférence
Une règle d’inférence est de la forme :
et signifie que pour assurer que la conclusion est vraie, il faut d’abord savoir que les prémisses , …, et sont vraies. Quand il n’y a pas de prémisses :
alors il n’y a rien à assurer pour conclure que est vraie.
Inversement, pour prouver qu’une certaine prémisse est vraie, il peut être nécessaire d’utiliser une autre règle d’inférence, ce qui nous donnerait quelque chose comme :
ce qui nous construit progressivement l’arbre de déduction de notre raisonnement. Dans notre raisonnement, les prémisses et conclusions manipulées seront généralement des triplets de Hoare.
Triplet de Hoare
Revenons sur la notion de triplet de Hoare :
Nous l’avons vu en début de tutoriel, ce triplet nous exprime que si avant l’exécution de , la propriété est vraie, et si termine, alors la propriété est vraie. Par exemple, si nous reprenons notre programme de calcul de la valeur absolue (légèrement modifié):
/*@
ensures \result >= 0;
ensures (val >= 0 ==> \result == val ) && (val < 0 ==> \result == -val);
*/
int abs(int val){
int res;
if(val < 0) res = - val;
else res = val;
return res;
}
Ce que nous dit Hoare, est que pour prouver notre programme, les propriétés entre accolades dans ce programme doivent être vérifiées (j’ai omis une des deux postconditions pour alléger la lecture) :
int abs(int val){
int res;
// { P }
if(val < 0){
// { (val < 0) && P }
res = - val;
// { \at(val, Pre) >= 0 ==> res == val && \at(val, Pre) < 0 ==> res == -val }
} else {
// { !(val < 0) && P }
res = val;
// { \at(val, Pre) >= 0 ==> res == val && \at(val, Pre) < 0 ==> res == -val }
}
// { \at(val, Pre) >= 0 ==> res == val && \at(val, Pre) < 0 ==> res == -val }
return res;
}
Cependant, Hoare ne nous dit pas comment nous pouvons obtenir automatiquement la
propriété P de ce programme. Ce que nous propose Dijkstra, c’est donc un moyen
de calculer, à partir d’une postcondition et d’une commande ou d’une liste de
commandes , la précondition minimale assurant après . Nous pourrions
donc, dans le programme précédent, calculer la propriété P qui nous donne les
garanties voulues.
Nous présenterons tout au long de cette partie les différents cas de la fonction qui, à une postcondition voulue et un programme ou une instruction, associe la plus faible précondition qui permet de l’assurer. Nous utiliserons cette notation pour définir le calcul correspondant à une ou plusieurs instructions :
De plus, la fonction est telle qu’elle nous garantit que le triplet de Hoare :
est effectivement un triplet valide.
Nous utiliserons souvent des assertions ACSL pour présenter les notions à venir :
//@ assert ma_propriete ;
Ces assertions correspondent en fait à des étapes intermédiaires possibles pour
les propriétés indiquées dans nos triplets de Hoare. Nous pouvons par exemple
reprendre le programme précédent et remplacer nos commentaires par les assertions
ACSL correspondantes (j’ai omis P car sa valeur est en fait simplement
« vrai ») :
int abs(int val){
int res;
if(val < 0){
//@ assert val < 0 ;
res = - val;
//@ assert \at(val, Pre) >= 0 ==> res == val && \at(val, Pre) < 0 ==> res == -val ;
} else {
//@ assert !(val < 0) ;
res = val;
//@ assert \at(val, Pre) >= 0 ==> res == val && \at(val, Pre) < 0 ==> res == -val ;
}
//@ assert \at(val, Pre) >= 0 ==> res == val && \at(val, Pre) < 0 ==> res == -val ;
return res;
}
[Formel] Concepts de base
Affectation
L’affectation est l’opération la plus basique que l’on puisse avoir dans un langage (mise à part l’opération « ne rien faire » qui manque singulièrement d’intérêt). Le calcul de plus faible précondition associé est le suivant :
où la notation signifie « la propriété où est remplacé par ». Ce qui correspond ici à « la postcondition où a été remplacé par ». Dans l’idée, pour que la formule en postcondition d’une affectation de à soit vraie, il faut qu’en remplaçant chaque occurrence de dans la formule par , on obtienne une propriété qui est vraie. Par exemple :
// { P }
x = 43 * c ;
// { x = 258 }
La fonction nous permet donc de calculer la plus faible précondition de l’opération (), ce que l’on peut réécrire sous la forme d’un triplet de Hoare :
// { 43*c = 258 }
x = 43 * c ;
// { x = 258 }
Pour calculer la précondition de l’affectation, nous avons remplacé chaque occurrence de dans la postcondition, par la valeur affectée. Si notre programme était de la forme:
int c = 6 ;
// { 43*c = 258 }
x = 43 * c ;
// { x = 258 }
nous pourrions alors fournir la formule « » à notre prouveur automatique
afin qu’il détermine si cette formule peut effectivement être satisfaite. Ce à quoi
il répondrait évidemment « oui », puisque cette propriété est très simple à vérifier.
En revanche, si nous avions donné la valeur 7 pour c, le prouveur nous répondrait
que non, une telle formule n’est pas vraie.
Nous pouvons donc écrire la règle d’inférence pour le triplet de Hoare de l’affectation, où l’on prend en compte le calcul de plus faible précondition :
Nous noterons qu’il n’y a pas de prémisse à vérifier. Cela veut-il dire que le triplet est nécessairement vrai ? Oui. Mais cela ne dit pas si la précondition est respectée par le programme où se trouve l’instruction, ni que cette précondition est possible. C’est ce travail qu’effectuent ensuite les prouveurs automatiques.
Par exemple, nous pouvons demander la vérification de la ligne suivante avec Frama-C :
int a = 42;
//@ assert a == 42;
Ce qui est, bien entendu, prouvé directement par Qed car c’est une simple application de la règle de l’affectation.
Notons que d’après la norme C, l’opération d’affectation est une expression
et non une instruction. C’est ce qui nous permet par exemple d’écrire
if( (a = foo()) == 42). Dans Frama-C, une affectation sera toujours une
instruction. En effet, si une affectation est présente au sein d’une
expression plus complexe, le module de création de l’arbre de syntaxe abstraite
du programme analysé effectue une étape de normalisation qui crée
systématiquement une instruction séparée.
Affectation de valeurs pointées
En C, grâce aux (à cause des ?) pointeurs, nous pouvons avoir des programmes avec des alias, à savoir que deux pointeurs peuvent pointer vers la même position en mémoire. Notre calcul de plus faible précondition doit donc considérer ce genre de cas. Par exemple, nous pouvons regarder ce triplet de Hoare :
//@ assert p = q ;
*p = 1 ;
//@ assert *p + *q == 2 ;
Ce triplet de Hoare est correct, puisque p et q sont en
alias, modifier la valeur *p modifie aussi la valeur *q,
par conséquent, ces deux expressions s’évaluent à et la postcondition est
vraie. Cependant, regardons ce que nous obtenons en appliquant le calcul de plus
faible précondition précédemment défini pour l’affectation sur cet exemple:
Nous obtenons la plus faible précondition: 1 + *q == 2, et donc
nous pourrions déduire que la plus faible précondition est *q == 1
(ce qui est vrai), mais nous ne sommes pas en mesure de conclure que le programme
est correct, car rien dans notre formule ne nous indique quelque chose comme:
p == q ==> *q == 1. En fait, ici, nous voudrions être capable de
calculer une plus faible précondition de la forme:
Pour cela, nous devons faire attention à la notion d’aliasing. Une manière commune de le faire est de considérer que la mémoire est une variable particulière du programme (nommons la ) sur laquelle nous pouvons effectuer deux opérations : obtenir la valeur d’un emplacement particulier en mémoire (qui nous retourne une expression) et changer la valeur à une position mémoire pour y placer une nouvelle valeur (qui nous retourne la nouvelle mémoire obtenue).
Notons :
- par la notation
- par la notation
Ces deux opérations peuvent être définies comme suit :
Si aucune valeur n’est associée à la position mémoire envoyée à , la valeur est indéfinie (la mémoire est une fonction partielle). Bien sûr, au début d’une fonction, cette mémoire peut être remplie avec un ensemble de positions mémoire pour lesquelles nous savons que la valeur a été précédemment définie (par exemple parce que la spécification de la fonction nous l’indique).
Maintenant, nous pouvons changer légèrement notre calcul de plus faible précondition pour le cas particulier des affectations à travers un pointeur. Pour cela, nous considérons que nous avons dans le programme une variable implicite qui modélise la mémoire, et nous définissons l’affectation d’une position en mémoire comme une mise à jour de cette variable, de telle manière à ce que cette position contienne maintenant l’expression fournie lors de l’affectation :
Évaluer une valeur pointée dans une formule consiste maintenant à utiliser l’opération pour demander la valeur à la mémoire. Nous pouvons donc appliquer notre calcul de plus faible précondition à notre programme précédent :
- nous devons appliquer la règle pour l’affectation de valeur pointée, mais pour cela, nous devons d’abord introduire ,
- nous remplaçons nos accès de pointeurs par un appel à sur ,
- nous appliquons le remplacement demandé par la règle d’affectation,
- nous utilisons la définition de pour (),
- nous utilisons la définition de pour \ ()
- nous appliquons quelques simplifications sur la formule …
- … et nous pouvons finalement conclure que ou .
et comme dans notre programme nous savons que , nous pouvons conclure que le programme est correct.
Le plugin WP ne fonctionne par exactement comme cela. En particulier, cela dépend du
modèle mémoire sélectionné pour réaliser la preuve, qui fait différentes hypothèses à
propos de la manière dont la mémoire est organisée. Pour le modèle mémoire que nous
utilisons, le modèle mémoire typé, WP crée différentes variables pour la mémoire.
Cela dit, regardons tout de même les conditions de vérification générées par WP pour la
postcondition de la fonction swap :
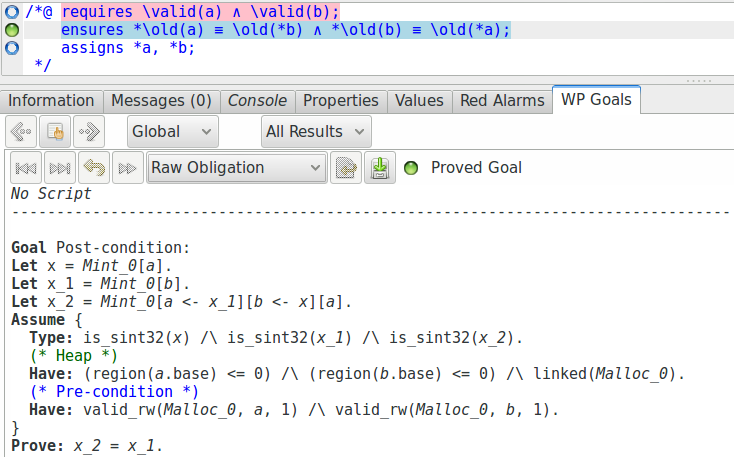
Nous pouvons voir, au début de la définition de cette condition de vérification qu’une
variable Mint_0 représentant une mémoire pour les valeurs de type entier
a été créée, et que cette mémoire est mise à jour et accédée à l’aide des opérateurs que
nous avons défini précédemment (voir par exemple la définition de la variable
x_2).
Séquence d’instructions
Pour qu’une instruction soit valide, il faut que sa précondition nous permette, par cette instruction, de passer à la postcondition voulue. Maintenant, nous avons besoin d’enchaîner ce processus d’une instruction à une autre. L’idée est alors que la postcondition assurée par la première instruction soit compatible avec la précondition demandée par la deuxième et que ce processus puisse se répéter pour la troisième instruction, etc.
La règle d’inférence correspondant à cette idée, utilisant les triplets de Hoare est la suivante:
Pour vérifier que la séquence d’instructions (NB : où et peuvent elles-mêmes être des séquences d’instructions), nous passons par une propriété intermédiaire qui est à la fois la précondition de et la postcondition de . Cependant, rien ne nous indique pour l’instant comment obtenir les propriétés et .
Le calcul de plus faible précondition nous dit simplement que la propriété intermédiaire est trouvée par calcul de plus faible précondition de la deuxième instruction. Et que la propriété est trouvée en calculant la plus faible précondition de la première instruction. La plus faible précondition de notre liste d’instruction est donc déterminée comme ceci :
Le plugin WP de Frama-C fait ce calcul pour nous, c’est pour cela que nous n’avons pas besoin d’écrire les assertions entre chaque ligne de code.
int main(){
int a = 42;
int b = 37;
int c = a+b; // i:1
a -= c; // i:2
b += a; // i:3
//@assert b == 0 && c == 79;
}
Arbre de preuve
Notons que lorsque nous avons plus de deux instructions, nous pouvons simplement considérer que la dernière instruction est la seconde instruction de notre règle et que toutes les instructions qui la précèdent forment la première « instruction ». De cette manière, nous remontons bien les instructions une à une dans notre raisonnement, par exemple avec le programme précédent :
|
| |
|
| |
| ||
Nous pouvons par calcul de plus faibles préconditions construire la propriété à partir de et , ce qui nous permet de déduire , à partir de et et finalement avec et .
Nous pouvons maintenant vérifier des programmes comprenant plusieurs instructions ; il est temps d’y ajouter un peu de structure.
Règle de la conditionnelle
Pour qu’un branchement conditionnel soit valide, il faut que la postcondition soit atteignable par les deux banches, depuis la même précondition, à ceci près que chacune des branches aura une information supplémentaire : le fait que la condition était vraie dans un cas et fausse dans l’autre.
Comme avec la séquence d’instructions, nous aurons donc deux points à vérifier (pour éviter de confondre les accolades, j’utilise la syntaxe ) :
Nos deux prémisses sont donc la vérification que lorsque nous avons la
précondition et que nous passons dans la branche if, nous atteignons bien la
postcondition, et que lorsque nous avons la précondition et que nous passons
dans la branche else, nous obtenons bien également la postcondition.
Le calcul de précondition de pour la conditionnelle est le suivant :
À savoir que doit impliquer la précondition la plus faible de , pour pouvoir l’exécuter sans erreur vers la postcondition, et que doit impliquer la précondition la plus faible de (pour la même raison).
Bloc else vide
En suivant cette définition, si le else ne fait rien, alors la règle
d’inférence est de la forme suivante, en remplaçant par une instruction
« ne rien faire ».
Le triplet pour le else est :
Ce qui veut dire que nous devons avoir :
En résumé, si la condition du if est fausse, cela veut dire que la
postcondition de l’instruction conditionnelle globale est déjà vérifiée avant de
rentrer dans le else (puisqu’il ne fait rien).
Par exemple, nous pourrions vouloir remettre une configuration à une valeur par défaut si elle a mal été configurée par un utilisateur du programme :
int c;
// ... du code ...
if(c < 0 || c > 15){
c = 0;
}
//@ assert 0 <= c <= 15;
Soit :
La formule est bien vérifiable : quelle que soit l’évaluation de l’implication sera vraie.
Bonus Stage - Règle de conséquence
Parfois, il peut être utile pour la preuve de renforcer une postcondition ou d’affaiblir une précondition. Si la première sera souvent établie par nos soins pour faciliter le travail du prouveur, la seconde est plus souvent vérifiée par l’outil à l’issue du calcul de plus faible précondition.
La règle d’inférence en logique de Hoare est la suivante :
(Nous noterons que les prémisses, ici, ne sont pas seulement des triplets de Hoare mais également des formules à vérifier)
Par exemple, si notre postcondition est trop complexe, elle risque de générer une plus faible précondition trop compliquée et de rendre le calcul des prouveurs difficile. Nous pouvons alors créer une postcondition intermédiaire , plus simple, mais plus restreinte et impliquant la vraie postcondition. C’est la partie .
Inversement, le calcul de précondition générera généralement une formule compliquée et souvent plus faible que la précondition que nous souhaitons accepter en entrée. Dans ce cas, c’est notre outil qui s’occupera de vérifier l’implication entre ce que nous voulons et ce qui est nécessaire pour que notre code soit valide. C’est la partie .
Nous pouvons par exemple illustrer cela avec le code qui suit. Notons bien qu’ici, le code pourrait tout à fait être prouvé par l’intermédiaire de WP sans ajouter des affaiblissements et renforcements de propriétés, car le code est très simple, il s’agit juste d’illustrer la règle de conséquence.
/*@
requires P: 2 <= a <= 8;
ensures Q: 0 <= \result <= 100 ;
assigns \nothing ;
*/
int constrained_times_10(int a){
//@ assert P_imply_WP: 2 <= a <= 8 ==> 1 <= a <= 9 ;
//@ assert WP: 1 <= a <= 9 ;
int res = a * 10;
//@ assert SQ: 10 <= res <= 90 ;
//@ assert SQ_imply_Q: 10 <= res <= 90 ==> 0 <= res <= 100 ;
return res;
}
(À noter ici : nous avons omis les contrôles de débordement d’entiers).
Ici, nous voulons avoir un résultat compris entre 0 et 100. Mais nous savons que
le code ne produira pas un résultat sortant des bornes 10 à 90. Donc nous
renforçons la postcondition avec une assertion que res, le résultat, est compris
entre 0 et 90 à la fin. Le calcul de plus faible précondition, sur cette propriété,
et avec l’affectation res = 10*a nous produit une plus faible précondition
1 <= a <= 9 et nous savons finalement que 2 <= a <= 8 nous donne cette garantie.
Quand une preuve a du mal à être réalisée sur un code plus complexe, écrire des
assertions produisant des postconditions plus fortes mais qui forment des formules
plus simples peut souvent nous aider. Notons que dans le code précédent, les lignes
P_imply_WP et SQ_imply_Q ne sont jamais utiles car c’est le raisonnement par
défaut produit par WP, elles sont juste présentes pour l’illustration.
Bonus Stage - Règle de constance
Certaines séquences d’instructions peuvent concerner et faire intervenir des variables différentes. Ainsi, il peut arriver que nous initialisions et manipulions un certain nombre de variables, que nous commencions à utiliser certaines d’entre elles, puis que nous les délaissions au profit d’autres pendant un temps. Quand un tel cas apparaît, nous avons envie que l’outil ne se préoccupe que des variables qui sont susceptibles d’être modifiées pour avoir des propriétés les plus légères possibles.
La règle d’inférence qui définit ce raisonnement est la suivante :
où ne modifie aucune variable entrant en jeu dans . Ce qui nous dit : « pour vérifier le triplet, débarrassons-nous des parties de la formule qui concernent des variables qui ne sont pas manipulées par et prouvons le nouveau triplet ». Cependant, il faut prendre garde à ne pas supprimer trop d’information, au risque de ne plus pouvoir prouver nos propriétés.
Par exemple, nous pouvons imaginer le code suivant (une nouvelle fois, nous omettons les contrôles de débordements au niveau des entiers) :
/*@
requires a > -99 ;
requires b > 100 ;
ensures \result > 0 ;
assigns \nothing ;
*/
int foo(int a, int b){
if(a >= 0){
a++ ;
} else {
a += b ;
}
return a ;
}
Si nous regardons le code du bloc if, il ne fait pas intervenir la variable
b, donc nous pouvons omettre complètement les propriétés à propos de b pour
réaliser la preuve que a sera bien supérieur à 0 après l’exécution du bloc :
/*@
requires a > -99 ;
requires b > 100 ;
ensures \result > 0 ;
assigns \nothing ;
*/
int foo(int a, int b){
if(a >= 0){
//@ assert a >= 0; //et rien à propos de b
a++ ;
} else {
a += b ;
}
return a ;
}
En revanche, dans le bloc else, même si b n’est pas modifiée, établir
des propriétés seulement à propos de a rendrait notre preuve impossible (en
tant qu’humains). Le code serait :
/*@
requires a > -99 ;
requires b > 100 ;
ensures \result > 0 ;
assigns \nothing ;
*/
int foo(int a, int b){
if(a >= 0){
//@ assert a >= 0; // et rien à propos de b
a++ ;
} else {
//@ assert a < 0 && a > -99 ; // et rien à propos de b
a += b ;
}
return a ;
}
Dans le bloc else, n’ayant que connaissance du fait que a est compris
entre -99 et 0, et ne sachant rien à propos de b, nous pourrions
difficilement savoir si le calcul a += b produit une valeur supérieure
strict à 0 pour a.
Naturellement ici, WP prouvera la fonction sans problème, puisqu’il transporte de lui-même les propriétés qui lui sont nécessaires pour la preuve. En fait, l’analyse des variables qui sont nécessaires ou non (et l’application, par conséquent de la règle de constance) est réalisée directement par WP.
Notons finalement que la règle de constance est une instance de la règle de conséquence :
Si les variables de n’ont pas été modifiées par l’opération (qui par contre, modifie les variables de pour former ), alors effectivement et .
Exercices
Une série d’affectations
Calculer à la main la plus faible précondition du programme suivant :
/*@
requires -10 <= x <= 0 ;
requires 0 <= y <= 5 ;
ensures -10 <= \result <= 10 ;
*/
int function(int x, int y){
int res ;
y += 10 ;
x -= 5 ;
res = x + y ;
return res ;
}
En utilisant la bonne règle d’inférence, en déduire que le programme respecte le contrat fixé pour cette fonction.
Branche then vide dans une conditionnelle
Nous avons précédemment montré que lorsqu’une structure conditionnelle a une branche
else vide, cela signifie que la conjonction de la précondition et de la négation
de la condition de notre structure conditionnelle est suffisante pour prouver la
postcondition de la structure conditionnelle.
Pour les deux questions qui suivent, nous avons uniquement besoin des règles d’inférence
et pas du calcul de plus faible précondition.
Montrer que lorsqu’au lieu de la branche else, c’est la branche then qui est
vide, la postcondition de structure conditionnelle est vérifiée par la conjonction de
la précondition et de la condition de notre structure conditionnelle (puisque
la branche « else » est la seule à potentiellement modifier l’état de
la mémoire).
Montrer que si les deux branches sont vide, la structure conditionnelle est juste une instruction skip.
Court-circuit (short-circuit)
Les compilateurs C implémentent le court-circuit pour les conditions (c’est d’ailleurs
imposé par le standard C). Par exemple, cela signifie qu’un code comme (sans
bloc else) :
if(cond1 && cond2){
// code
}
peut être ré-écrit comme :
if(cond1){
if(cond2){
// code
}
}
Montrer que sur ces deux morceaux de code, le calcul de plus faible précondition
génère une plus faible précondition pour tout code qui se trouverait dans le bloc
then. Notons que nous supposons que les conditions sont pures (ne modifient aucune
position en mémoire).
Un plus gros programme
Calculer à la main la plus faible précondition du programme suivant :
/*@
requires -5 <= y <= 5 ;
requires -5 <= x <= 5 ;
ensures -15 <= \result <= 25 ;
*/
int function(int x, int y){
int res ;
if(x < 0){
x = 0 ;
}
if(y < 0){
x += 5 ;
} else {
x -= 5 ;
}
res = x - y ;
return res ;
}
En utilisant la bonne règle d’inférence, en déduire que le programme respecte le contrat fixé pour cette fonction.
Les boucles
Les boucles ont besoin d’un traitement de faveur dans la vérification déductive de programmes. Ce sont les seules structures de contrôle qui vont nécessiter un travail conséquent de notre part. Nous ne pouvons pas y échapper car sans les boucles nous pouvons difficilement prouver des programmes intéressants.
Avant de s’intéresser à la spécification des boucles, il est légitime de se poser la question suivante : pourquoi les boucles sont-elles compliquées ?
Induction et invariance
La nature des boucles rend leur analyse difficile. Lorsque nous faisons nos raisonnements arrières, il nous faut une règle capable de dire à partir de la postcondition quelle est la précondition d’une certaine séquence d’instructions. Problème : nous ne pouvons a priori pas déduire combien de fois la boucle s’exécutera et donc, nous ne pouvons pas non plus savoir combien de fois les variables ont été modifiées.
Nous procéderons donc en raisonnant par induction. Nous devons trouver une propriété qui est vraie avant de commencer la boucle et qui, si elle est vraie au début d’un tour de boucle, sera vraie à la fin (et donc par extension, au début du tour suivant). Quand la boucle termine, nous gagnons la connaissance que la condition de boucle est fausse qui, en conjonction avec l’invariant, doit nous permettre de prouver que la postcondition de la boucle est vérifiée.
Ce type de propriété est appelé un invariant de boucle. Un invariant de boucle est une propriété qui doit être vraie avant et après chaque tour d’une boucle, et plus précisément chaque fois que l’on évalue la condition de la boucle. Par exemple, pour la boucle :
for(int i = 0 ; i < 10 ; ++i){ /* */ }
La propriété est un invariant de la boucle. La propriété est également un invariant de la boucle (qui est nettement plus imprécis néanmoins). La propriété n’est pas un invariant, elle n’est pas vraie à l’entrée de la boucle. La propriété n’est pas un invariant de la boucle, elle n’est pas vraie à la fin du dernier tour de la boucle qui met la valeur à .
Le raisonnement produit par l’outil pour vérifier un invariant sera donc :
- vérifions que est vrai au début de la boucle (établissement),
- vérifions que est vrai avant de commencer un tour, auquel cas est vrai après (préservation).
[Formel] Règle d’inférence
En notant l’invariant , la règle d’inférence correspondant à la boucle est définie comme suit :
Et le calcul de plus faible précondition est le suivant :
Détaillons cette formule :
- (1) le premier correspond à l’établissement de l’invariant, c’est vulgairement la « précondition » de la boucle,
- la deuxième partie de la conjonction ()
correspond à la vérification du travail effectué par le corps de la boucle :
- la précondition que nous connaissons du corps de la boucle (notons , « Known WP ») , c’est (). Soit le fait que nous sommes rentrés dedans ( est vrai), et que l’invariant est respecté à ce moment (, qui est vrai avant de commencer la boucle par 1, et dont veut vérifier qu’il sera vrai en fin de bloc de la boucle (2)),
- (2) ce qu’il nous reste à vérifier c’est que implique la précondition réelle* du bloc de code de la boucle (). Ce que nous voulons en fin de bloc, c’est avoir maintenu l’invariant ( n’est peut-être plus vrai en revanche). Donc , soit ,
- * cela correspond à une application de la règle de conséquence expliquée précédemment.
- finalement, la dernière partie () nous dit que le fait d’être sorti de la boucle (), tout en ayant maintenu l’invariant , doit impliquer la postcondition voulue pour la boucle.
Dans ce calcul, nous pouvons noter que la fonction ne nous donne aucune indication sur le moyen d’obtenir l’invariant . Nous allons donc devoir spécifier manuellement de telles propriétés à propos de nos boucles.
Retour à l’outil
Il existe des outils capables d’inférer des invariants (pour peu qu’ils soient simples, les outils automatiques restent limités). Ce n’est pas le cas de WP. Il nous faut donc écrire nos invariants à la main. Trouver et écrire les invariants des boucles de nos programmes sera toujours la partie la plus difficile de notre travail lorsque nous chercherons à prouver des programmes.
En effet, si en l’absence de boucle, la fonction de calcul de plus faible précondition peut nous fournir automatiquement les propriétés vérifiables de nos programmes, ce n’est pas le cas pour les invariants de boucle pour lesquels nous n’avons pas accès à une procédure automatique de calcul. Nous devons donc trouver et formuler correctement ces invariants, et selon l’algorithme, celui-ci peut parfois être très subtil.
Pour indiquer un invariant à une boucle, nous ajoutons les annotations suivantes en début de boucle :
int main(){
int i = 0;
/*@
loop invariant 0 <= i <= 30;
*/
while(i < 30){
++i;
}
//@assert i == 30;
}
RAPPEL : L’invariant est bien : i 30 !
Pourquoi ? Parce que tout au long de la boucle i sera bien compris entre
0 et 30 inclus. 30 est même la valeur qui nous permettra de sortir de la
boucle. Plus encore, une des propriétés demandées par le calcul de plus faible
préconditions sur les boucles est que lorsque l’on invalide la condition de la
boucle, par la connaissance de l’invariant, on peut prouver la postcondition
(Formellement : ).
La postcondition de notre boucle est i == 30 et doit être impliquée par
i < 30 0 <= i <= 30. Ici, cela fonctionne
bien : i >= 30 && 0 <= i <= 30 ==> i == 30. Si l’invariant excluait
l’égalité à 30, la postcondition ne serait pas atteignable.
Une nouvelle fois, nous pouvons jeter un œil à la liste des buts dans « WP Goals » :
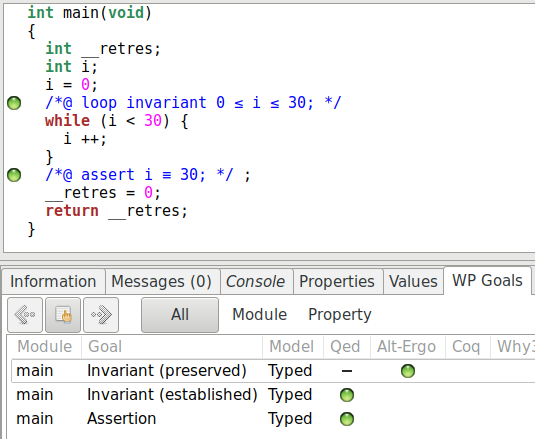
Nous remarquons bien que WP décompose la preuve de l’invariant en deux parties :
l’établissement de l’invariant et sa préservation. WP produit exactement le
raisonnement décrit plus haut pour la preuve de l’assertion. Dans les versions
récentes de Frama-C, Qed est devenu particulièrement puissant, et l’obligation de
preuve générée ne le montre pas (affichant simplement « True »). En utilisant
l’option -wp-no-simpl au lancement, nous pouvons quand même voir
l’obligation correspondante :
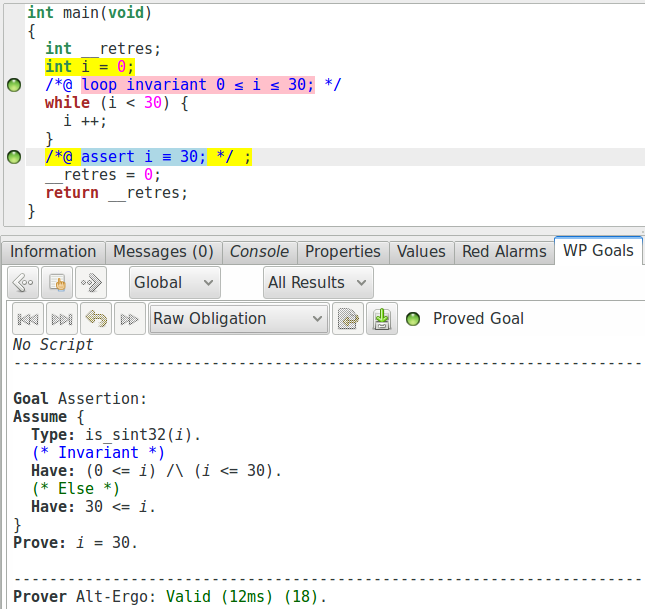
Mais notre spécification est-elle suffisante ?
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 30;
*/
while(i < 30){
++i;
}
//@assert i == 30;
//@assert h == 42;
}
Voyons le résultat :
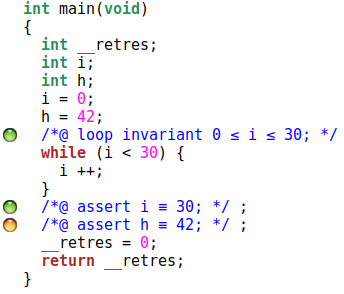
Il semble que non.
La clause « assigns » … pour les boucles
En fait, à propos des boucles, WP ne considère vraiment que ce que lui
fournit l’utilisateur pour faire ses déductions. Et ici l’invariant ne nous dit
rien à propos de l’évolution de la valeur de h. Nous pourrions signaler
l’invariance de toute variable du programme mais ce serait beaucoup d’efforts.
ACSL nous propose plus simplement d’ajouter des annotations assigns pour
les boucles. Toute autre variable est considérée invariante. Par exemple :
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 30;
loop assigns i;
*/
while(i < 30){
++i;
}
//@assert i == 30;
//@assert h == 42;
}
Cette fois, nous pouvons établir la preuve de correction de la boucle. Par contre, rien ne nous prouve sa terminaison. L’invariant de boucle n’est pas suffisant pour effectuer une telle preuve. Par exemple, dans notre programme, si nous réécrivons la boucle comme ceci :
/*@
loop invariant 0 <= i <= 30;
loop assigns i;
*/
while(i < 30){
}
L’invariant est bien vérifié également, mais nous ne pourrons jamais prouver que la boucle se termine : elle est infinie.
Correction partielle et correction totale - Variant de boucle
En vérification déductive, il y a deux types de correction, la correction partielle et la correction totale. Dans le premier cas, la formulation est « si la précondition est validée et si le calcul termine, alors la postcondition est validée ». Dans le second cas, « si la précondition est validée, alors le calcul termine et la postcondition est validée ». WP s’intéresse par défaut à de la preuve de correction partielle :
void foo(){
while(1){}
//assert \false;
}
Si nous demandons la vérification de ce code en activant le contrôle de RTE, nous obtenons ceci :
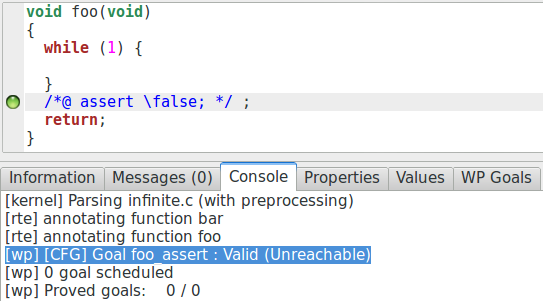
L’assertion « FAUX » est prouvée ! La raison est simple : la non-terminaison de la boucle est triviale : la condition de la boucle est « VRAI » et aucune instruction du bloc de la boucle ne permet d’en sortir puisque le bloc ne contient pas de code du tout. Comme nous sommes en correction partielle, et que le calcul ne termine pas, nous pouvons prouver n’importe quoi au sujet du code qui suit la partie non terminante. Si, en revanche, la non-terminaison est non-triviale, il y a peu de chances que l’assertion soit prouvée.
À noter qu’une assertion inatteignable est toujours prouvée comme vraie de cette
manière :
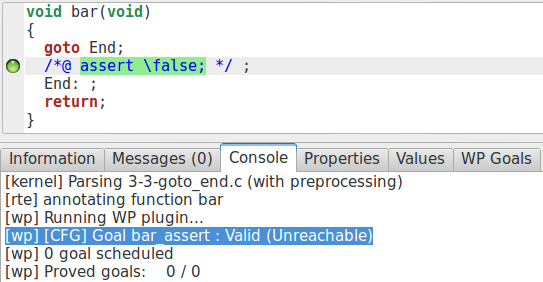
C’est également le cas lorsque l’on sait trivialement qu’une instruction
produit nécessairement une erreur d’exécution (par exemple en déréférençant
la valeur NULL), comme nous avions déjà pu le constater avec l’exemple
de l’appel à abs avec la valeur INT_MIN.
Pour prouver la terminaison d’une boucle, nous utilisons la notion de variant de boucle. Le variant de boucle n’est pas une propriété mais une valeur. C’est une expression faisant intervenir des éléments modifiés par la boucle et donnant une borne supérieure sur le nombre d’itérations restant à effectuer à un tour de la boucle. C’est donc une expression supérieure à 0 et strictement décroissante d’un tour de boucle à l’autre (cela sera également vérifié par induction par WP).
Si nous reprenons notre programme précédent, nous pouvons ajouter le variant de cette façon :
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 30;
loop assigns i;
loop variant 30 - i;
*/
while(i < 30){
++i;
}
//@assert i == 30;
//@assert h == 42;
}
Une nouvelle fois nous pouvons regarder les buts générés :
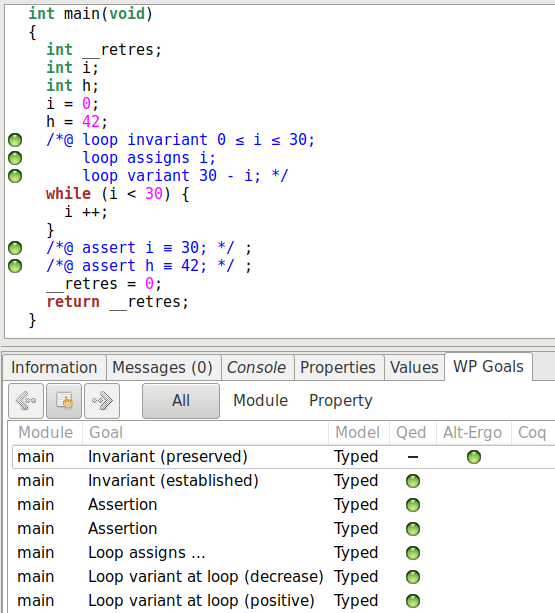
Le variant nous génère bien deux obligations au niveau de la vérification :
assurer que la valeur est positive, et assurer qu’elle décroît strictement pendant
l’exécution de la boucle. Si nous supprimons la ligne de code qui incrémente
i, WP ne peut plus prouver que la valeur 30 - i décroît strictement.
Il est également bon de noter qu’être capable de donner un variant de boucle n’induit pas nécessairement d’être capable de donner le nombre exact d’itérations qui doivent encore être exécutées par la boucle, car nous n’avons pas toujours une connaissance aussi précise du comportement de notre programme. Nous pouvons par exemple avoir un code comme celui-ci :
#include <stddef.h>
/*@
ensures min <= \result <= max;
*/
size_t random_between(size_t min, size_t max);
void undetermined_loop(size_t bound){
/*@
loop invariant 0 <= i <= bound ;
loop assigns i;
loop variant i;
*/
for(size_t i = bound; i > 0; ){
i -= random_between(1, i);
}
}
Ici, à chaque tour de boucle, nous diminuons la valeur de la variable i par une
valeur dont nous savons qu’elle se trouve entre 1 et i. Nous pouvons donc bien
assurer que la valeur de i est positive et décroît strictement, mais nous ne
pouvons pas dire combien de tours de boucles vont être réalisés pendant une
exécution.
Le variant n’est donc bien qu’une borne supérieure sur le nombre d’itérations de la boucle.
Notons aussi que le variant de boucle n’a besoin d’être positif qu’au début de l’exécution du bloc de la boucle. Donc, dans le code suivant :
int i = 5 ;
while(i >= 0){
i -= 2 ;
}
Même si i peut être négatif lorsque la boucle termine, cette valeur est
bien un variant de la boucle puisque nous n’exécutons pas le corps de la boucle à
nouveau.
Lier la postcondition et l’invariant
Supposons le programme spécifié suivant. Notre but est de prouver que le retour
de cette fonction est l’ancienne valeur de a à laquelle nous avons ajouté 10.
/*@
ensures \result == \old(a) + 10;
*/
int plus_dix(int a){
/*@
loop invariant 0 <= i <= 10;
loop assigns i, a;
loop variant 10 - i;
*/
for (int i = 0; i < 10; ++i)
++a;
return a;
}
Le calcul de plus faibles préconditions ne permet pas de sortir de la boucle des informations qui ne font pas partie de l’invariant. Dans un programme comme :
/*@
ensures \result == \old(a) + 10;
*/
int plus_dix(int a){
++a;
++a;
++a;
//...
return a;
}
en remontant les instructions depuis la postcondition, on conserve toujours les
informations à propos de a. À l’inverse, comme mentionné plus tôt, en dehors de
la boucle WP ne considérera que les informations fournies par notre invariant.
Par conséquent, notre fonction plus_dix ne peut pas être prouvée en l’état :
l’invariant ne mentionne rien à propos de a. Pour lier notre
postcondition à l’invariant, il faut ajouter une telle information. Par
exemple :
/*@
ensures \result == \old(a) + 10;
*/
int plus_dix(int a){
/*@
loop invariant 0 <= i <= 10;
loop invariant a = \old(a) + i; //< AJOUT
loop assigns i, a;
loop variant 10 - i;
*/
for (int i = 0; i < 10; ++i)
++a;
return a;
}
Ce besoin peut apparaître comme une contrainte très forte. Il ne l’est en fait pas
tant que cela. Il existe des analyses fortement automatiques capables de
calculer les invariants de boucles. Par exemple, sans spécification, une
interprétation abstraite calculera assez facilement 0 <= i <= 10 et
\old(a) <= a <= \old(a)+10. En revanche, il est souvent bien plus difficile
de calculer les relations qui existent entre des variables différentes qui
évoluent dans le même programme, par exemple l’égalité mentionnée par notre
invariant ajouté.
Terminaison prématurée de boucle
Un invariant de boucle doit être vrai chaque fois que la condition de la boucle est évaluée. En fait, cela signifie aussi qu’elle doit être vraie avant chaque itération, et après chaque itération complète. Illustrons cette idée importante avec un exemple.
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 30;
loop assigns i;
loop variant 30 - i;
*/
while(i < 30){
++i;
if(i == 30) break ;
}
//@assert i == 30;
//@assert h == 42;
}
Dans cette fonction, quand la boucle atteint l’indice 30, elle effectue une opération
break avant que la condition de la boucle soit à nouveau testée.
L’invariant que nous avons écrit est bien sûr vérifié, mais nous pouvons en fait le
restreindre encore.
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 29;
loop assigns i;
loop variant 30 - i;
*/
while(i < 30){
++i;
if(i == 30) break ;
}
//@assert i == 30;
//@assert h == 42;
}
Ici, nous pouvons voir que nous avons exclu 30 de la plage des valeurs de
i et la fonction est correctement vérifiée par WP. Cette propriété
est particulièrement intéressante, car elle ne s’applique pas qu’à l’invariant.
Aucune des propriétés de la boucle n’ont besoin d’être vérifiées pendant l’itération
qui mène au break. Par exemple, nous pouvons écrire ce code qui est
également vérifié :
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 29;
loop assigns i;
loop variant 30 - i;
*/
while(i < 30){
++i;
if(i == 30){
i = 42 ;
h = 84 ;
break ;
}
}
//@assert i == 42;
//@assert h == 84;
}
Nous voyons que nous pouvons écrire la variable h même si elle
n’est pas listée dans la clause loop assigns, et que nous pouvons
donner la valeur 42 à i alors que l’invariant l’interdirait, et aussi
que nous pouvons rendre l’expression du variant négative. En fait, tout se passe
exactement comme si nous avions écrit :
int main(){
int i = 0;
int h = 42;
/*@
loop invariant 0 <= i <= 30;
loop assigns i;
loop variant 30 - i;
*/
while(i < 30){
++i;
}
//@assert i == 30;
//@assert h == 42;
}
C’est un schéma très pratique. Il correspond à tout algorithme qui cherche, à l’aide d’une boucle, une condition vérifiée par un élément particulier dans une structure de données et s’arrête quand cet élément est trouvé afin d’effectuer certaines opérations qui ne sont finalement pas vraiment des opérations de la boucle. D’un point de vue vérification, cela nous permet de simplifier le contrat associé à une boucle : nous savons que l’opération (potentiellement complexe) ) réalisée juste avant de sortir de la boucle ne nécessite pas d’être prise en compte dans l’invariant.
Exercices
Invariant de boucle
Écrire un invariant de boucle pour la boucle suivante et prouver qu’il est respecté en utilisant la commande :
frama-c -wp your-file.c
int x = 0 ;
while(x > -10){
-- x ;
}
Est-ce que la propriété est un invariant correct ? Expliquer pourquoi.
Loop variant
Écrire un invariant et un variant corrects pour la boucle suivante et prouver l’ensemble à l’aide de la commande :
frama-c -wp your-file.c
int x = -20 ;
while(x < 0){
x += 4 ;
}
Si le variant ne donne pas précisément le nombre d’itérations restantes, ajouter une variable qui enregistre exactement le nombre d’itérations restantes et l’utiliser comme variant. Il est possible qu’un invariant supplémentaire soit nécessaire.
Loop assigns
Écrire une clause loop assigns pour cette boucle, de manière à ce
que l’assertion ligne 8 soit prouvée ainsi que la clause loop assigns.
Ignorons les erreurs à l’exécution dans cet exercice.
int h = 42 ;
int x = 0 ;
int e = 0 ;
while(e < 10){
++ e ;
x += e * 2 ;
}
//@ assert h == 42 ;
Lorsque la preuve réussit, supprimer la clause loop assigns et
trouver un autre moyen d’assurer que l’assertion soit vérifiée en utilisant des
annotations différentes (notons qu’un nouveau label C peut être nécessaire dans
le code). Que peut-on déduire à propos de la clause loop assigns ?
Terminaison prématurée
Écrire un contrat de boucle pour cette boucle qui permette de prouver les assertions aux lignes 8 et 9 ainsi que le contrat de boucle.
int i ;
int x = 0 ;
for(i = 0 ; i < 20 ; ++i){
if(i == 19){
x++ ;
break ;
}
}
//@ assert x == 1 ;
//@ assert i == 19 ;
Plus d'exemples sur les boucles
Exemple avec un tableau read-only
S’il y a une structure de données que nous traitons avec les boucles, c’est bien le tableau. C’est une bonne base d’exemples pour les boucles, car ils permettent rapidement de présenter des invariants intéressants et surtout, ils nous permettront d’introduire des constructions très importantes d’ACSL.
Prenons par exemple la fonction qui cherche une valeur dans un tableau :
#include <stddef.h>
/*@
requires 0 < length;
requires \valid_read(array + (0 .. length-1));
assigns \nothing;
behavior in:
assumes \exists size_t off ; 0 <= off < length && array[off] == element;
ensures array <= \result < array+length && *\result == element;
behavior notin:
assumes \forall size_t off ; 0 <= off < length ==> array[off] != element;
ensures \result == NULL;
disjoint behaviors;
complete behaviors;
*/
int* search(int* array, size_t length, int element){
/*@
loop invariant 0 <= i <= length;
loop invariant \forall size_t j; 0 <= j < i ==> array[j] != element;
loop assigns i;
loop variant length-i;
*/
for(size_t i = 0; i < length; i++)
if(array[i] == element) return &array[i];
return NULL;
}
Cet exemple est suffisamment fourni pour introduire des notations importantes.
D’abord, comme nous l’avons déjà mentionné, le prédicat \valid_read (de
même que \valid) nous permet de spécifier non seulement la validité d’une
adresse en lecture mais également celle de tout un ensemble d’adresses
contiguës. C’est la notation que nous avons utilisée dans cette expression :
//@ requires \valid_read(a + (0 .. length-1));
Cette précondition nous atteste que les adresses a+0, a+1 …, a+length-1
sont valides en lecture.
Nous avons également introduit deux notations qui vont nous être très utiles, à
savoir \forall () et \exists (), les
quantificateurs de la logique. Le premier nous servant à annoncer que pour tout
élément, la propriété suivante est vraie. Le second pour annoncer qu’il existe
un élément tel que la propriété est vraie. Si nous commentons les deux lignes en
questions, nous pouvons les lire de cette façon :
/*@
//pour tout "off" de type "size_t", tel que SI "off" est compris entre 0 et "length"
// ALORS la case "off" de "a" est différente de "element"
\forall size_t off ; 0 <= off < length ==> a[off] != element;
//il existe "off" de type "size_t", tel que "off" soit compris entre 0 et "length"
// ET que la case "off" de "a" vaille "element"
\exists size_t off ; 0 <= off < length && a[off] == element;
*/
Si nous devions résumer leur utilisation, nous pourrions dire que sur un certain
ensemble d’éléments, une propriété est vraie, soit à propos d’au moins l’un
d’eux, soit à propos de la totalité d’entre eux. Un schéma qui reviendra
typiquement dans ce cas est que nous restreindrons cet ensemble à travers une
première propriété (ici : 0 <= off < length) puis nous voudrons prouver la
propriété réelle qui nous intéresse à propos d’eux. Mais il y a une
différence fondamentale entre l’usage de exists et celui de forall.
Avec \forall type a ; p(a) ==> q(a), la restriction (p) est suivie
par une implication. Pour tout élément, s’il respecte une première propriété
(p), alors il doit vérifier la seconde propriété q. Si nous mettions un ET
comme pour le « il existe » (que nous expliquerons ensuite), cela voudrait dire que
nous voulons que tout élément respecte à la fois les deux propriétés. Parfois,
cela peut être ce que nous voulons exprimer, mais cela ne correspond alors plus
à l’idée de restreindre un ensemble dont nous voulons montrer une propriété
particulière.
Avec \exists type a ; p(a) && q(a), la restriction (p) est suivie
par une conjonction, nous voulons qu’il existe un élément tel que cet élément
est dans un certain état (défini par p), tout en respectant l’autre
propriété q. Si nous mettions une implication comme pour le « pour tout »,
alors une telle expression devient toujours vraie à moins que p soit une
tautologie ! Pourquoi ? Existe-t-il « a » tel que p(a) implique q(a) ? Prenons
n’importe quel « a » tel que p(a) est faux, l’implication devient vraie.
Cette partie de l’invariant mérite une attention particulière :
//@ loop invariant \forall size_t j; 0 <= j < i ==> array[j] != element;
En effet, c’est la partie qui définit l’action de notre boucle, elle indique à
WP ce que la boucle fera (ou apprendra dans le cas présent) tout au long de
son exécution. Ici en l’occurrence, cette formule nous dit qu’à chaque tour, nous
savons que pour toute case entre 0 et la prochaine que nous allons visiter (i exclue), elle stocke une valeur différente de l’élément recherché.
Le but de WP associé à la préservation de cet invariant est un peu compliqué, il n’est pour nous pas très intéressant de se pencher dessus. En revanche, la preuve de l’établissement de cet invariant est intéressante :
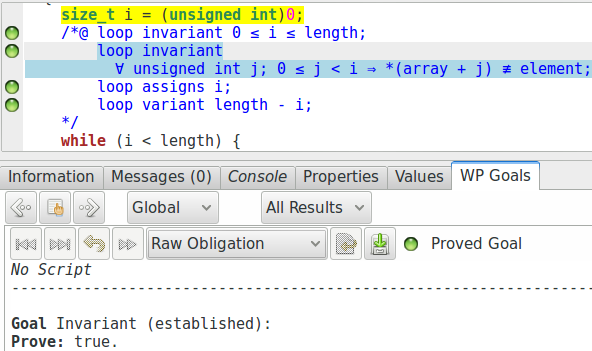
Nous constatons que cette propriété, pourtant complexe, est prouvée par
Qed sans aucun problème. Si nous regardons sur quelles parties du programme la
preuve se base, nous voyons l’instruction i = 0 surlignée, et c’est
bien la dernière instruction que nous effectuons sur i avant de commencer
la boucle. Et donc effectivement, si nous faisons le remplacement dans la formule
de l’invariant :
//@ loop invariant \forall size_t j; 0 <= j < 0 ==> array[j] != element;
« Pour tout j, supérieur ou égal à 0 et inférieur strict à 0 », cette partie est nécessairement fausse. Notre implication est donc nécessairement vraie.
Exemples avec tableaux mutables
Nous allons voir deux exemples avec la manipulation de tableaux en mutation. L’un avec une modification totale, l’autre en modification sélective.
Remise à zéro
Regardons la fonction effectuant la remise à zéro d’un tableau.
#include <stddef.h>
/*@
requires \valid(array + (0 .. length-1));
assigns array[0 .. length-1];
ensures \forall size_t i; 0 <= i < length ==> array[i] == 0;
*/
void raz(int* array, size_t length){
/*@
loop invariant 0 <= i <= length;
loop invariant \forall size_t j; 0 <= j < i ==> array[j] == 0;
loop assigns i, array[0 .. length-1];
loop variant length-i;
*/
for(size_t i = 0; i < length; ++i)
array[i] = 0;
}
Nous voyons que nous utilisons pour l’invariant une structure assez similaire
à ce que nous avons utilisé pour l’exemple précédent: nous indiquons un premier
invariant pour contraindre la valeur de i, et un autre qui exprime
à chaque itération ce que nous avons appris depuis le début de l’exécution de la
boucle (tous les éléments visités sont à ). Finalement, intéressons-nous à la
clause loop assigns: à nouveau, nous utilisons la notation
n .. m pour indiquer quelle partie du tableau a été modifiée.
Chercher et remplacer
Le dernier exemple qui nous intéresse est l’algorithme « chercher et remplacer ». C’est un algorithme qui modifie sélectivement des valeurs dans une certaine plage d’adresses. Il est toujours un peu difficile de guider l’outil dans ce genre de cas car, d’une part, nous devons garder « en mémoire » ce qui est modifié et ce qui ne l’est pas et, d’autre part, parce que l’induction repose sur ce fait.
À titre d’exemple, la première spécification que nous pouvons réaliser pour cette fonction ressemblerait à ceci :
#include <stddef.h>
/*@
requires \valid(array + (0 .. length-1));
assigns array[0 .. length-1];
ensures \forall size_t i; 0 <= i < length && \old(array[i]) == old
==> array[i] == new;
ensures \forall size_t i; 0 <= i < length && \old(array[i]) != old
==> array[i] == \old(array[i]);
*/
void search_and_replace(int* array, size_t length, int old, int new){
/*@
loop invariant 0 <= i <= length;
loop invariant \forall size_t j; 0 <= j < i && \at(array[j], Pre) == old
==> array[j] == new;
loop invariant \forall size_t j; 0 <= j < i && \at(array[j], Pre) != old
==> array[j] == \at(array[j], Pre);
loop assigns i, array[0 .. length-1];
loop variant length-i;
*/
for(size_t i = 0; i < length; ++i){
if(array[i] == old) array[i] = new;
}
}
Nous utilisons la fonction logique \at(v, Label) qui nous donne la valeur de
la variable v au point de programme Label. Si nous regardons l’utilisation qui
en est faite ici, nous voyons que dans l’invariant de boucle, nous cherchons à
établir une relation entre les anciennes valeurs du tableau et leurs potentielles
nouvelles valeurs :
/*@
loop invariant \forall size_t j; 0 <= j < i && \at(array[j], Pre) == old
==> array[j] == new;
loop invariant \forall size_t j; 0 <= j < i && \at(array[j], Pre) != old
==> array[j] == \at(array[j], Pre);
*/
Pour tout élément que nous avons visité, s’il valait la valeur qui doit être
remplacée, alors il vaut la nouvelle valeur, sinon il n’a pas changé. Alors que
nous nous reposions sur la clause assigns pour ce genre de propriété
dans les exemples précédents, ici nous ne pouvons pas le faire. Même si ACSL nous
permettrait d’exprimer cette propriété de manière très précise, WP ne pourrait pas
vraiment en tirer parti, dû à la manière dont cette clause est traitée. Nous devons
donc utiliser un invariant et conserver une approximation des positions mémoire
affectées.
En fait, si nous essayons de prouver l’invariant, WP n’y parvient pas. Dans ce genre de cas, le plus simple est encore d’ajouter diverses assertions exprimant les propriétés intermédiaires que nous nous attendons à voir facilement prouvées et impliquant l’invariant. En fait, nous nous apercevons rapidement que WP n’arrive pas à maintenir le fait que nous n’avons pas encore modifié la fin du tableau :
for(size_t i = 0; i < length; ++i){
//@assert array[i] == \at(array[i], Pre); // échec de preuve
if(array[i] == old) array[i] = new;
}
Nous pouvons donc ajouter cette information comme invariant :
/*@
loop invariant 0 <= i <= length;
loop invariant \forall size_t j; 0 <= j < i && \at(array[j], Pre) == old
==> array[j] == new;
loop invariant \forall size_t j; 0 <= j < i && \at(array[j], Pre) != old
==> array[j] == \at(array[j], Pre);
//La fin du tableau n'a pas été modifiée :
loop invariant \forall size_t j; i <= j < length
==> array[j] == \at(array[j], Pre);
loop assigns i, array[0 .. length-1];
loop variant length-i;
*/
for(size_t i = 0; i < length; ++i){
if(array[i] == old) array[i] = new;
}
Et cette fois, la preuve passera.
Exercices
Pour tous ces exercices, utiliser la commande suivante pour démarrer la vérification:
frama-c-gui -wp -wp-rte -warn-unsigned-overflow -warn-unsigned-downcast your-file.c
Fonctions sans modification : Forall, Exists, …
Actuellement, les pointeurs de fonction ne sont pas directement supportés par WP. Considérons que nous avons une fonction :
/*@
assigns \nothing ;
ensures \result <==> // some property about value
*/
int pred(int value){
// your code
}
Écrire un corps de son choix pour cette fonction et un contrat l’accompagnant.
Ensuite, écrire les fonctions suivantes avec leurs contrats pour prouver leur
correction. Notons qu’il n’est pas possible d’utiliser la fonction C dans un
contrat, la propriété choisie pour la fonction pred
devra donc être inlinée dans la spécification des différentes fonctions.
forall_predretourne vrai si et seulement sipredest vraie pour tous les éléments ;exists_predretourne vrai si et seulement sipredest vraie pour au moins un élément ;none_predretourne vrai si et seulement sipredest fausse pour tous les éléments ;some_not_predretourne vrai si et seulement sipredest fausse pour au moins un élément.
Les deux dernières fonctions devraient être écrites en appelant seulement les deux premières.
Fonction sans modification : Égalité de plages de valeurs
Écrire, spécifier et prouver la fonction equal qui retourne vrai
si et seulement si deux plages de valeurs sont égales. Écrire, en utilisant la
fonction equal, le code de different qui retourne vrai
si et seulement si deux plages de valeurs sont différentes, la postcondition
devrait contenir un quantificateur existentiel.
int equal(const int* a_1, const int* a_2, size_t n){
}
int different(const int* a_1, const int* a_2, size_t n){
}
Fonction sans modification : recherche dichotomique
La fonction suivante cherche la position d’une valeur fournie en entrée dans un tableau, en supposant que le tableau est trié. D’abord, considérons que la longueur du tableau est fournie en tant qu’int et utilisons des valeurs de ce même type pour gérer les indices. Nous pouvons noter qu’il y a deux comportements à cette fonction : soit la valeur existe dans le tableau (et le résultat est l’indice de cette valeur) ou pas (et le résultat est -1).
/*@
requires Sorted:
\forall integer i, j ; 0 <= i <= j < len ==> arr[i] <= arr[j] ;
*/
int bsearch(int* arr, int len, int value){
if(len == 0) return -1 ;
int low = 0 ;
int up = len-1 ;
while(low <= up){
int mid = low + (up - low)/2 ;
if (arr[mid] > value) up = mid-1 ;
else if(arr[mid] < value) low = mid+1 ;
else return mid ;
}
return -1 ;
}
Cette fonction est un petit peu complexe à prouver, voici quelques conseils
pour en venir à bout. D’abord, la longueur de la fonction est reçue en utilisant
un type int, donc nous devons poser une restriction sur cette longueur en
précondition pour qu’elle soit cohérente. Ensuite, l’un des invariants de la
boucle devrait indiquer les bornes des valeurs low et
up, mais nous pouvons noter que pour chacune d’elles, l’une des
bornes n’est pas nécessaire. Finalement, la seconde propriété invariante
devrait indiquer que si l’un des indices du tableau correspond à la valeur
recherchée, alors cet indice devrait être correctement borné.
Plus dur : Modifier cette fonction de façon à recevoir len
comme un size_t. Il faut modifier légèrement l’algorithme et
la spécification/les invariants. Conseil : s’arranger pour que up
soit une borne exclue de la recherche.
Fonction avec modification : addition de vecteurs
Écrire, spécifier et prouver la fonction qui ajoute deux vecteurs dans un troisième. Fixer des contraintes arbitraires sur les valeurs d’entrée pour gérer le débordement des entiers. Considérer que le vecteur est résultant est spatialement séparé des vecteurs d’entrée. En revanche, le même vecteur devrait pouvoir être utilisé pour les deux vecteurs d’entrée.
void add_vectors(int* v_res, const int* v1, const int* v2, size_t len){
}
Fonction avec modification : inverse
Écrire, spécifier et prouver la fonction qui inverse un vecteur en place.
Prendre garde à la partie non-modifiée du vecteur à une itération donnée de la
boucle. Utiliser la fonction swap précédemment prouvée.
void swap(int* a, int* b);
void reverse(int* array, size_t len){
}
Fonction avec modification : copie
Écrire, spécifier et prouver la fonction copy qui copie une plage
de valeur dans un autre tableau, en commençant pas la première cellule du
tableau. Considérer (et spécifier) dans un premier temps que les deux plages
sont entièrement séparées.
void copy(int const* src, int* dst, size_t len){
}
Plus dur : Les vraies fonctions copy et copy_backward.
En fait, une séparation aussi forte n’est pas nécessaire. Pour faire une copie en partant du début, la précondition réelle doit simplement garantir que si les deux plages se chevauchent en mémoire, le début de la destination ne doit pas être dans la plage source :
//@ requires \separated(&src[0 .. len-1], dst) ;
Essentiellement, en copiant des éléments dans cet ordre, nous pouvons les
décaler depuis la fin d’une plage vers le début. En revanche, cela signifie que
nous devons être plus précis dans notre contrat : nous ne garantissons plus une
égalité avec le tableau source mais avec les anciennes valeurs du tableau
source. Nous devons également être plus précis dans notre invariant, d’abord en
spécifiant aussi la relation avec l’état précédent de la mémoire, et ensuite en
ajoutant un invariant qui nous dit que le tableau source n’est pas modifié entre
le i élément visité et le dernier.
Finalement, il est aussi possible d’écrire une fonction qui copie les éléments de
la fin vers le début. Dans ce cas, à nouveau, les plages de valeurs peuvent se
chevaucher, mais la condition n’est pas exactement la même. Écrire, spécifier et
prouver la fonction copy_backward qui copie les éléments dans le
sens inverse.
Appels de fonctions
Appel de fonction
[Formel] Calcul de plus faible précondition
Lorsqu’une fonction est appelée, le contrat de cette fonction est utilisé pour déterminer la précondition de l’appel, mais il est important de garder en tête deux aspects important pour exprimer le calcul de plus faible précondition.
Premièrement, la postcondition d’une fonction qui serait appelée dans un
programme n’est pas nécessairement directement la précondition calculée pour le code
qui suit l’appel à . Par exemple, si nous avons un programme:
x = f() ; c , et si alors que
la postcondition de la fonction f est , nous avons
besoin d’exprimer l’affaiblissement de la précondition réelle de c
vers celle que l’on a calculé. Pour cela, nous renvoyons à la
section sur la règle de conséquence, l’idée est simplement de vérifier
que la postcondition de la fonction implique la précondition calculée.
Deuxièmement, en C, une fonction peut avoir des effets de bord. Par conséquent, les valeurs référencées en entrée de fonction ne restent pas nécessairement les mêmes après l’appel à la fonction, et le contrat devrait exprimer certaines propriétés à propos des valeurs avant et après l’appel. Donc, si nous avons des labels © dans la postcondition, nous devons faire les remplacements qui s’imposent par rapport au lieu d’appel.
Pour définir le calcul de plus faible précondition associé aux fonctions, introduisons d’abord quelques notations pour rendre les explications plus claires. Pour cela, considérons l’exemple suivant :
/*@ requires \valid(x) && *x >= 0 ;
assigns *x ;
ensures *x == \old(*x)+1 ; */
void inc(int* x);
void foo(int* a){
L1:
inc(a) ;
L2:
}
Le calcul de plus faible précondition de l’appel de fonction nous demande de
considérer le contrat de la fonction appelée (ici, dans foo, quand
nous appelons la fonction inc). Bien sûr, avant l’appel de la fonction
nous devons vérifier sa précondition, qui fait donc partie de la plus faible
précondition. Mais nous devons aussi considérer la postcondition de la fonction,
sinon cela voudrait dire que nous ne prenons pas en compte son effet sur l’état du
programme.
Par conséquent, il est important de noter que dans la précondition, l’état mémoire
considéré est bien celui pour lequel la plus faible précondition doit être vraie,
tandis que pour la postcondition, ce n’est pas le cas: l’état considéré est celui
qui suit l’appel, alors que dans la postcondition, lorsque nous parlons des valeurs
avant l’appel nous devons explicitement ajouter le mot-clé
\old. Par exemple, pour le contrat de inc
lorsque nous l’appelons depuis foo, *x dans la
précondition est *a au label L1, alors que *x
dans la postcondition est *a au label L2. Par conséquent,
la pré et la postcondition doivent être considérées de manières légèrement différentes
lorsque nous devons parler des positions mémoire mutables. Notons que pour la valeur
du paramètre x lui même, ce n’est pas le cas : cette valeur ne peut pas
être modifiée par l’appel (du point de vue de l’appelant).
Maintenant, définissons le calcul de plus faible précondition d’un appel de fonction. Pour cela, notons:
- un vecteur de valeurs et la valeur,
- les arguments fournis à la fonction lors de l’appel,
- les paramètres dans la définition de la fonction,
- les valeurs modifiées (vues de l’extérieur, une fois instanciées),
- une valeur en postcondition,
- une valeur en précondition.
Nous nommons la précondition de la fonction, et , la postcondition.
Nous pouvons détailler les étapes du raisonnement dans les différentes parties de cette formule.
Premièrement, notons que dans les pré et postconditions, chaque paramètre
est remplacé par l’argument correspondant (), comme nous
l’avons dit juste avant, nous n’avons pas de question d’état mémoire à considérer
ici puisque ces valeurs ne peuvent pas être changées par l’appel de fonction. Par
exemple dans le contrat de inc, chaque occurrence de x
serait remplacée par l’argument a.
Ensuite, dans la partie de notre formule qui correspond à la postcondition, nous
pouvons voir que nous introduisons un . Le but ici est de modéliser
la possibilité que la fonction change la valeur des positions mémoire spécifiées par
la clause assigns du contrat. Donc, pour chaque position potentiellement
modifiée (qui est, pour notre exemple d’appel à inc,
*(&a)), nous générons une valeur qui représente sa valeur après
l’appel. Mais si nous voulons vérifier que la postcondition nous donne le bon
résultat, nous ne pouvons pas accepter toute valeur pour les positions mémoire
modifiées, nous voulons celles qui permettent de satisfaire la postcondition.
Nous utilisons donc ces valeurs pour transformer la postcondition de la fonction et pour vérifier qu’elle implique la postcondition reçue en entrée du calcul de plus faible précondition. Nous faisons cela en remplaçant, pour chaque position mémoire modifiée , sa valeur avec la valeur qu’elle obtient après l’appel (). Finalement, nous devons remplacer chaque valeur par sa valeur avant l’appel, et pour chaque , cette valeur est simplement ().
[Formel] Exemple
Illustrons tout cela sur un exemple en appliquant le calcul de plus faible
précondition sur ce petit code, en supposant le contrat précédemment proposé pour
la fonction swap.
int a = 4 ;
int b = 2 ;
swap(&a, &b) ;
//@ assert a == 2 && b == 4 ;
Nous pouvons appliquer le calcul de plus faible précondition :
Et considérons séparément :
Par la clause assigns, nous savons que les valeurs modifiées par la
fonction sont et . (nous raccourcissons avec
et avec ).
Pour la précondition, nous obtenons : Pour la postcondition, commençons par écrire l’expression depuis laquelle nous travaillerons avant de faire les remplacements (et sans la syntaxe de remplacement pour rester concis) : Remplaçons d’abord les pointeurs () : Puis les valeurs , avec les valeurs quantifiées () : Et les valeurs , avec les valeurs avant l’appel () : Nous pouvons maintenant simplifier cette formule en :
Donc, est : Nous pouvons immédiatement simplifier cette formule en constatant que les propriétés de validité sont trivialement vraies (puisque les variables sont allouées sur la pile juste avant) :
Maintenant, calculons , en remplaçant d’abord par par la règle d’affectation : et ensuite par par la même règle :
Cette dernière propriété est trivialement vraie, le programme est vérifié.
Que devrions-nous garder en tête ?
Les fonctions sont absolument nécessaires pour programmer modulairement, et le calcul de plus faible précondition est pleinement compatible avec cette idée, permettant de raisonner localement à propos de chaque fonction et donc de composer les preuves juste de la même manière que nous composons les appels de fonction.
Comme pense-bête, nous devrions toujours garder en tête le schéma suivant :
/*@
requires foo_R ;
assigns ... ;
ensures foo_E ;
*/
type foo(parameters...){
// Ici, nous supposons que foo_R est vérifiée
// Ici, nous devons prouver que bar_R est vérifiée
bar(some parameters ...) ;
// Ici, nous supposons que bar_E est vérifiée
// Ici nous devons prouver que foo_E est vérifiée
return ... ;
}
Notons qu’à propos du dernier commentaire, en calcul de plus faible précondition, l’idée est plutôt de montrer que notre précondition est assez forte pour assurer que le code nous amène à la postcondition. Cependant, premièrement, cette vision est plus facile à comprendre et deuxièmement, un greffon comme WP (et comme n’importe quel outil réaliste pour la preuve de programme) ne suit pas strictement un calcul de plus faible précondition mais une manière fortement optimisée de calculer les conditions de vérification qui ne suit pas exactement les mêmes règles.
Fonctions récursives
WP ne vérifie pas encore la terminaison des fonctions. Bien sûr, si une fonction est seulement composée de boucles qui terminent (dont le variant indiqué est vérifié) et d’appels de fonctions qui elles-mêmes terminent, elle termine. En revanche, parfois ce raisonnement est insuffisant, comme dans le cas des fonctions récursives et mutuellement récursives. C’est la terminaison de ces fonctions qui n’est pas encore vérifiée par WP.
Cela signifie que nous pouvons, par mégarde, prouver n’importe quoi, si l’on définit et prouve une fonction qui ne termine pas.
/*@
assigns \nothing ;
ensures \false ;
*/
void trick(){
trick() ;
}
int main(){
trick();
//@ assert \false ;
}
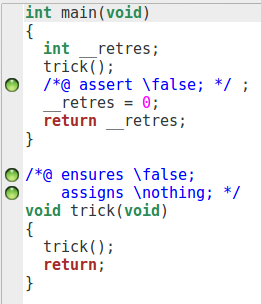
Nous pouvons voir que la fonction et l’assertion sont prouvées. Et, effectivement, la preuve est correcte : nous considérons une correction partielle (puisque nous ne pouvons pas prouver la terminaison), et cette fonction ne termine pas. Toute assertion suivant cette fonction est vraie : elle est inatteignable.
Une question que l’on peut alors se poser est : que peut-on faire dans un tel
cas ? Nous pouvons à nouveau utiliser une notion de variant pour borner le nombre
d’appels récursifs. En ACSL, c’est le rôle de la clause decreases :
/*@
requires n >= 0 ;
decreases n ;
*/
void ends(int n){
if(n > 0) ends(n-1);
}
Cette clause exprime essentiellement la même idée que le loop variant.
L’expression spécifiée par la clause decreases est une valeur positive
qui décroît strictement à chaque nouvel appel récursif de la fonction. Cependant,
cette clause n’est pas encore supportée par WP, donc nous ne pouvons pas encore
faire la preuve totale d’une fonction récursive avec le greffon WP.
Dans cette partie nous avons pu voir comment se traduisent les affectations et les structures de contrôle d’un point de vue logique. Nous nous sommes beaucoup attardés sur les boucles parce que c’est là que se trouvent la majorité des difficultés lorsque nous voulons spécifier et prouver un programme par vérification déductive, les annotations ACSL qui leur sont spécifiques nous permettent d’exprimer le plus précisément possible leur comportement.
Pour la suite, nous nous attarderons plus précisément sur les constructions que nous offre le langage ACSL du côté de la logique. Elles sont très importantes parce que ce sont elles qui vont nous permettre de nous abstraire du code pour avoir des spécifications plus compréhensibles et plus aisément prouvables.