Méthodologies de preuve - Introduction à la preuve de programmes C avec Frama-C et son greffon WP • Bibliothèque • Zeste de Savoir

Maintenant que nous avons présenté les fonctionnalités les plus importantes d’ACSL pour la preuve de programme, intéressons-nous plus spécifiquement à la manière de prouver un programme avec Frama-C et WP. Nous présenterons différentes approches qui peuvent être utilisées, selon la cible de vérification, le type de propriétés que l’on cherche à montrer et les fonctionnalités d’ACSL que nous utilisons.

Absence d'erreurs à l'exécution : contrats minimaux
Assertions de guidage et déclenchement de lemmes
Plus de code fantôme, fonctions lemmes et macros lemmes

Absence d'erreurs à l'exécution : contrats minimaux

Nous avons vu que la preuve d’un programme permet de vérifier deux aspects principaux à propos de sa correction ; d’abord que le programme ne contient pas d’erreur d’exécution, et ensuite que le programme répond correctement à sa spécification. Cependant, il est parfois difficile d’obtenir le second aspect, et le premier est déjà une étape intéressante pour la correction de notre programme.

En effet, les erreurs à l’exécution entraînent souvent la présence des fameux undefined behaviors dans les programmes C. Ces comportements peuvent être des vecteurs de failles de sécurité. Par conséquent, garantir leur absence nous protège déjà d’un grand nombre de ces vecteurs d’attaques. L’absence d’erreur à l’exécution peut être vérifiée avec WP à l’aide d’une approche appelée « contrats minimaux ».

Principe

L’approche par contrats minimaux est guidée par l’usage du greffon RTE de Frama-C. L’idée est simple : pour toutes les fonctions d’un module ou d’un projet, nous générons les assertions nécessaires à la vérification de l’absence d’erreurs à l’exécution , et nous écrivons ensuite l’ensemble des spécifications (correctes) qui sont suffisantes pour prouver ces assertions et les contrats ainsi rédigés. La plupart du temps, cela permet d’avoir beaucoup moins de lignes de spécifications que ce qui est nécessaire pour prouver la correction fonctionnelle du programme.

Commençons par un exemple simple avec la fonction valeur absolue.

int abs(int x){
  return (x < 0) ? -x : x ;
}

Ici, nous pouvons générer les assertions nécessaires à prouver pour montrer l’absence d’erreurs à l’exécution, ce qui génère ce programme :

/* Generated by Frama-C */
int abs(int x)
{
  int tmp;
  if (x < 0) 
    /*@ assert rte: signed_overflow: -2147483647 ≤ x; */
    tmp = - x;
  else tmp = x;
  return tmp;
}

Donc nous avons seulement besoin de spécifier la précondition qui nous dit que x doit être plus grand que INT_MIN :

/*@ 
  requires x > INT_MIN ;
*/
int abs(int x){
  return (x < 0) ? -x : x ;
}

Cette condition est suffisante pour montrer l’absence d’erreurs à l’exécution dans cette fonction.

Comme nous le verrons plus tard, généralement une fonction est cependant utilisée dans un contexte particulier. Il est donc probable que ce contrat ne soit en réalité pas suffisant pour assurer la correction dans son contexte d’appel. Par exemple, il est commun en C d’avoir des variables globales ou des pointeurs, il est donc probable que nous devions spécifier ce qui est assigné par la fonction. La plupart du temps, les clauses assigns ne peuvent pas être ignorées (ce qui est prévisible dans un langage où tout est mutable par défaut). De plus, si une personne demande la valeur absolue d’un entier, c’est probablement qu’elle a besoin d’une valeur positive. En réalité, le contrat ressemblera probablement à ceci :

/*@ 
  requires x > INT_MIN ;
  assigns  \nothing ;
  ensures  \result >= 0 ;
*/
int abs(int x){
  return (x < 0) ? -x : x ;
}

Mais cette addition ne devrait être guidée que par la vérification du ou des contexte dans lesquels la fonction est appelée, une fois que nous avons prouvé l’absence d’erreur d’exécution dans cette fonction.

Exemple: la fonction recherche

Maintenant que nous avons le principe en tête, travaillons avec un exemple un peu plus complexe. Celui-ci en particulier nécessite une boucle.


#include <stddef.h>

int* search(int* array, size_t length, int element){
  for(size_t i = 0; i < length; i++)
    if(array[i] == element) return &array[i];
  return NULL;
}

Lorsque nous générons les assertions liées aux erreurs à l’exécution, nous obtenons le programme suivant :

/* Generated by Frama-C */
#include "stddef.h"
int *search(int *array, size_t length, int element)
{
  int *__retres;
  {
    size_t i = (unsigned int)0;
    while (i < length) {
      /*@ assert rte: mem_access: \valid_read(array + i); */
      if (*(array + i) == element) {
        __retres = array + i;
        goto return_label;
      }
      i += (size_t)1;
    }
  }
  __retres = (int *)0;
  return_label: return __retres;
}

Nous devons prouver que toute cellule visitée par le programme peut être lue, nous avons donc besoin d’exprimer comme précondition que ce tableau est \valid_read sur la plage de valeurs correspondante. Cependant, ce n’est pas suffisant pour terminer la preuve puisque nous avons une boucle dans ce programme. Nous devons donc aussi fournir un invariant, nous voulons aussi probablement prouver que la boucle termine.

Nous obtenons donc la fonction suivante, spécifiée minimalement :

#include <stddef.h>

/*@
  requires \valid_read(array + (0 .. length-1)) ;
*/
int* search(int* array, size_t length, int element){
  /*@
    loop invariant 0 <= i <= length ;
    loop assigns i ;
    loop variant length - i ;
  */
  for(size_t i = 0; i < length; i++)
    if(array[i] == element) return &array[i];
  return NULL;
}

Ce contrat peut être comparé avec le contrat fourni pour la fonction de recherche de la section sur les boucles, et nous pouvons voir qu’il est beaucoup plus simple.

Maintenant imaginons que cette fonction est utilisée dans le programme suivant :

void foo(int* array, size_t length){
  int* p = search(array, length, 0) ;
  if(p){
    *p += 1 ;
  }
}

Nous devons à nouveau fournir un contrat pour cette fonction, à nouveau en regardant l’assertion générée par le plugin RTE :

void foo(int *array, size_t length)
{
  int *p = search(array,length,0);
  if (p) 
    /*@ assert rte: mem_access: \valid(p); */
    /*@ assert rte: mem_access: \valid_read(p); */
    /*@ assert rte: signed_overflow: *p + 1 ≤ 2147483647; */
    (*p) ++;
  return;
}

Nous devons donc vérifier que :

le pointeur que nous avons reçu est valide,
*p+1 ne fait pas de débordement,
nous respectons le contrat de la fonction search.

En plus du contrat de foo, nous devons fournir plus d’informations dans le contrat de search. En effet, nous ne pourrons pas prouver que le pointeur est valide si la fonction ne nous garantit pas qu’il est dans la plage correspondant à notre tableau dans ce cas. De plus, nous ne pourrons pas prouver que *p| a une valeur inférieure à INT_MAX si la fonction peut modifier le tableau.

Cela nous amène donc au programme complet annoté suivant :

#include <stddef.h>
#include <limits.h>

/*@
  requires \valid_read(array + (0 .. length-1)) ;
  assigns \nothing ;
  ensures \result == NULL ||
          (\exists integer i ; 0 <= i < length && array+i == \result) ;
*/
int* search(int* array, size_t length, int element){
  /*@
    loop invariant 0 <= i <= length ;
    loop assigns i ;
    loop variant length - i ;
  */
  for(size_t i = 0; i < length; i++)
    if(array[i] == element) return &array[i];
  return NULL;
}

/*@
  requires \forall integer i ; 0 <= i < length ==> array[i] < INT_MAX ;
  requires \valid(array + (0 .. length-1)) ;
*/
void foo(int *array, size_t length){
  int *p = search(array,length,0);
  if (p){
    *p += 1 ;
  }
}

Avantages et limitations

L’avantage le plus évident de cette approche est le fait qu’elle permet de garantir qu’un programme ne contient pas d’erreurs à l’exécution dans toute fonction d’un module ou d’un programme en (relative) isolation des autres fonctions. De plus, cette absence d’erreurs à l’exécution est garantie pour tout usage de la fonction dont l’appel respecte ses préconditions. Cela permet de gagner une certaine confiance dans un système avec une approche dont le coût est relativement raisonnable.

Cependant, comme nous avons pu le voir, lorsque nous utilisons une fonction, cela peut changer les connaissances que nous avons besoin d’avoir à son sujet, nécessitant d’enrichir son contrat progressivement. Nous pouvons par conséquent atteindre un point où nous avons prouvé la correction fonctionnelle de la fonction.

De plus, prouver l’absence d’erreur à l’exécution peut parfois ne pas être trivial comme nous avons pu le voir précédemment avec des fonctions comme la factorielle ou la somme des N premiers entiers, qui nécessitent de donner une quantité notable d’information aux solveurs SMT pour montrer qu’elle ne déborde pas.

Finalement, parfois les contrats minimaux d’une fonction ou d’un module sont simplement la spécification fonctionnelle complète. Et dans ce cas, effectuer la vérification d’absence d’erreur à l’exécution correspond à réaliser la vérification fonctionnelle complète du programme. C’est communément le cas lorsque nous devons travailler avec des structures de données complexes où les propriétés dont nous avons besoin pour montrer l’absence d’erreurs à l’exécution dépendent du comportement fonctionnel des fonctions, maintenant des invariants non triviaux à propos de la structure de donnée.

Exercices

Exemple simple

Prouver l’absence d’erreurs à l’exécution dans le programme suivant en utilisant une approche par contrats minimaux :

void max_ptr(int* a, int* b){
  if(*a < *b){
    int tmp = *b ;
    *b = *a ;
    *a = tmp ;
  }
}

void min_ptr(int* a, int* b){
  max_ptr(b, a);
}

void order_3_inc_min(int* a, int* b, int* c){
  min_ptr(a, b) ;
  min_ptr(a, c) ;
  min_ptr(b, c) ;
}

void incr_a_by_b(int* a, int const* b){
  *a += *b;
}

Inverse

Prouver l’absence d’erreurs à l’exécution dans la fonction reverse suivante et ses dépendances en utilisant une approche par contrats minimaux. Notons que la fonction swap doit également être spécifiée par contrats minimaux. Ne pas oublier d’ajouter les options -warn-unsigned-overflow et -warn-unsigned-downcast.


#include <stddef.h>

void swap(int* a, int* b){
  int tmp = *a;
  *a = *b;
  *b = tmp;
}

void reverse(int* array, size_t len){
  for(size_t i = 0 ; i < len/2 ; ++i){
    swap(array+i, array+len-i-1) ;
  }
}

Recherche dichotomique

Prouver l’absence d’erreurs à l’exécution dans la fonction bsearch suivante en utilisant une approche par contrats minimaux. Ne pas oublier d’ajouter les options -warn-unsigned-overflow et -warn-unsigned-downcast.

#include <stddef.h>

size_t bsearch(int* arr, size_t len, int value){
  if(len == 0) return -1 ;
  
  size_t low = 0 ;
  size_t up = len ;

  while(low < up){
    size_t mid = low + (up - low)/2 ;
    if     (arr[mid] > value) up = mid ;
    else if(arr[mid] < value) low = mid+1 ;
    else return mid ;
  }
  return -1 ;
}

Tri

Prouver l’absence d’erreurs à l’exécution dans la fonction sort et ses dépendances en utilisant une approche par contrats minimaux. Notons que ces dépendances doivent également être spécifiées par contrats minimaux. Ne pas oublier d’ajouter les options -warn-unsigned-overflow et -warn-unsigned-downcast.

#include <stddef.h>

size_t min_idx_in(int* a, size_t beg, size_t end){
  size_t min_i = beg;
  for(size_t i = beg+1; i < end; ++i){
    if(a[i] < a[min_i]) min_i = i;
  }
  return min_i;
}

void swap(int* p, int* q){
  int tmp = *p; *p = *q; *q = tmp;
}

void sort(int* a, size_t beg, size_t end){
  for(size_t i = beg ; i < end ; ++i){
    size_t imin = min_idx_in(a, i, end);
    swap(&a[i], &a[imin]);
  }
}

Assertions de guidage et déclenchement de lemmes

Il y a différents niveaux d’automatisation dans la vérification de programmes, depuis les outils complètement automatiques, comme les interpréteurs abstraits qui ne nécessitent aucune aide de la part de l’utilisateur (ou en tout cas, très peu), jusqu’aux outils interactifs comme les assistants de preuve, où les preuves sont principalement écrites à la main et l’outil est juste là pour vérifier que nous le faisons correctement.

Les outils comme WP (et beaucoup d’autres comme Why3, Spark, …) visent à maximiser l’automatisation. Cependant, plus les propriétés que nous voulons prouver sont complexes, plus il sera difficile d’obtenir automatiquement toute la preuve. Par conséquent, nous devons souvent aider les outils pour terminer la vérification. Nous faisons souvent cela en fournissant plus d’annotations pour aider le processus de génération des obligations de preuve. Ajouter un invariant de boucle est par exemple une manière de fournir les informations nécessaires pour produire le raisonnement par induction permettant son analyse, alors que les prouveurs automatiques sont plutôt mauvais à cet exercice.

Cette technique de vérification a été appelée « auto-active ». Ce mot est la contraction de « automatic » et « interactive ». Elle est automatique au sens où la majorité de la preuve est effectuée par des outils automatiques, mais elle est aussi en partie interactive puisqu’en tant qu’utilisateurs, nous fournissons manuellement de l’information aux outils.

Dans cette section, nous allons voir plus en détails comment nous pouvons utiliser des assertions pour guider la preuve. En ajoutant des assertions, nous créons une certaine base de connaissances (des propriétés que nous savons vraies), qui sont collectées par le générateur d’obligations de preuve pendant le calcul de WP et qui sont données aux prouveurs automatiques qui ont par conséquent plus d’information et peuvent potentiellement prouver des propriétés plus complexes.

Contexte de preuve

Pour comprendre exactement le bénéfice que représente l’ajout d’assertions dans les annotations d’un programme, commençons par regarder de plus près les obligations de preuve générées par WP à partir du code source annoté et comment les assertions sont prises en compte. Pour cela, nous allons utiliser le prédicat suivant (qui ressemble furieusement au théorème de Pythagore) :

/*@
  predicate rectangle{L}(integer c1, integer c2, integer h) =
    c1 * c1 + c2 * c2 == h * h ;
*/

Regardons d’abord cet exemple :

/*@
  requires \separated(x, y , z);
  requires 3 <= *x <= 5 ;
  requires 4 <= *y <= 5 ;
  requires *z <= 5 ;
  requires *x+2 == *y+1 == *z ;
*/
void example_1(int* x, int* y, int* z){
  //@ assert rectangle(*x, *y, *z);
  //@ assert rectangle(2* (*x), 2* (*y), 2* (*z));
}

Ici, nous avons spécifié une précondition suffisamment complexe pour que WP ne puisse par directement deviner les valeurs en entrée de fonction. En fait, ces valeurs sont exactement : *x == 3, *y == 4 et *z == 5. Maintenant, si nous regardons l’obligation de preuve générée pour notre première assertion, nous pouvons voir ceci (il faut bien sélectionner la vue « Full Context » ou « Raw obligation » - elles ne sont pas exactement identiques mais assez similaires, la première est juste légèrement plus jolie) :

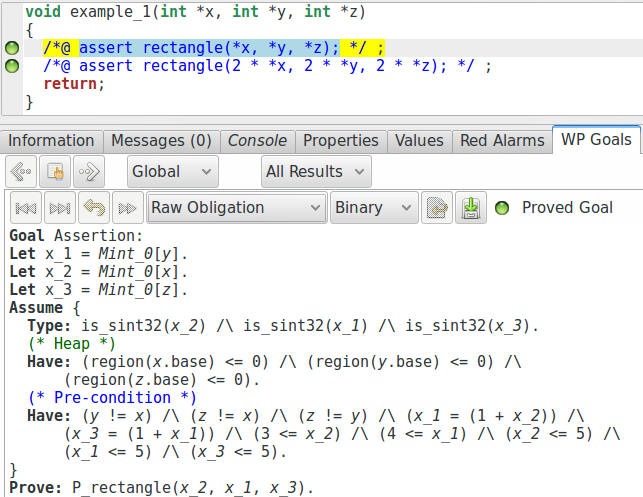
Nous y voyons les différentes contraintes que nous avons formulées comme préconditions de fonction (notons que les valeurs ne sont pas exactement les mêmes, et que quelques propriétés supplémentaires ont été générées). Maintenant, regardons plutôt l’obligation de preuve générées pour la seconde assertion (notons que nous avons édité les captures d’écran restantes de cette section pour nous concentrer sur ce qui est important, les autres propriétés pouvant être ignorées dans notre cas) :

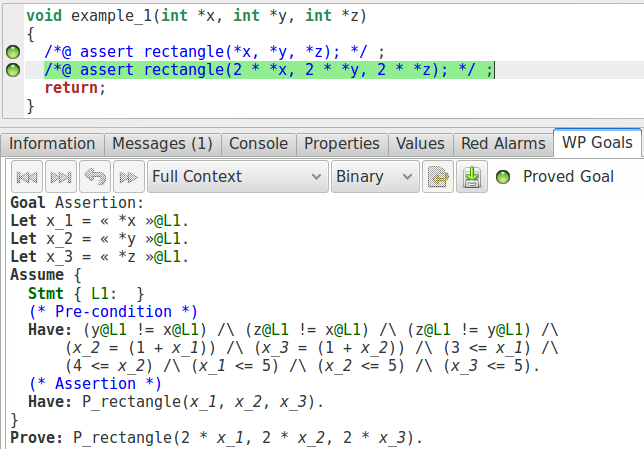
Ici, nous pouvons voir que dans le contexte utilisable pour la preuve de la seconde assertion, WP a collecté et ajouté la première assertion et en a fait une supposition. WP considère que les solveurs SMT peuvent supposer que cette propriété est vraie. Cela signifie que les prouveurs peuvent l’utiliser, mais également qu’elle doit être prouvée pour l’obligation de preuve actuelle soit complètement vérifiée.

Notons que WP ne collecte que ce qu’il trouve sur les différents chemins d’exécution qui permettent d’atteindre l’assertion. Par exemple, si nous modifions le code de telle manière à ce que le chemin qui mène à la seconde assertion saute le chemin qui passe par la première, celle-ci n’apparaît pas dans le contexte de la seconde assertion.

void example_1_p(int* x, int* y, int* z){
  goto next;
  //@ assert rectangle(*x, *y, *z);
 next: ;
  //@ assert rectangle(2* (*x), 2* (*y), 2* (*z));
}

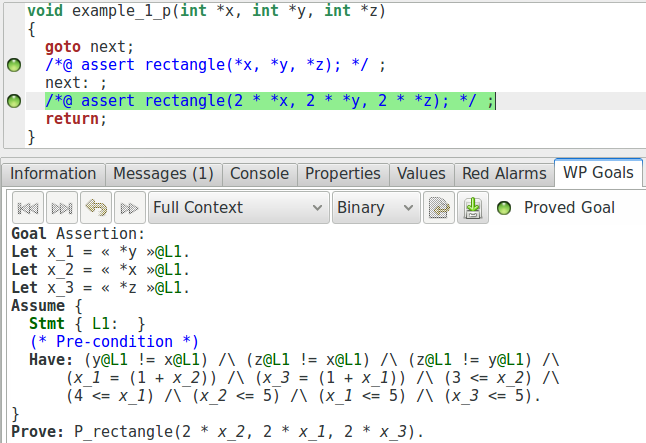
Maintenant, modifions un peu notre exemple de manière à illustrer comment les assertions peuvent changer la manière de prouver un programme. Par exemple, nous pouvons modifier les différentes positions mémoire (en doublant chaque valeur) et vérifier que le triangle résultant est rectangle.

/*@
  requires \separated(x, y , z);
  requires 3 <= *x <= 5 ;
  requires 4 <= *y <= 5 ;
  requires *z <= 5 ;
  requires *x+2 == *y+1 == *z ;
*/
void example_2(int* x, int* y, int* z){
  *x += 3 ;
  *y += 4 ;
  *z += 5 ;

  //@ assert rectangle(*x, *y, *z);
}

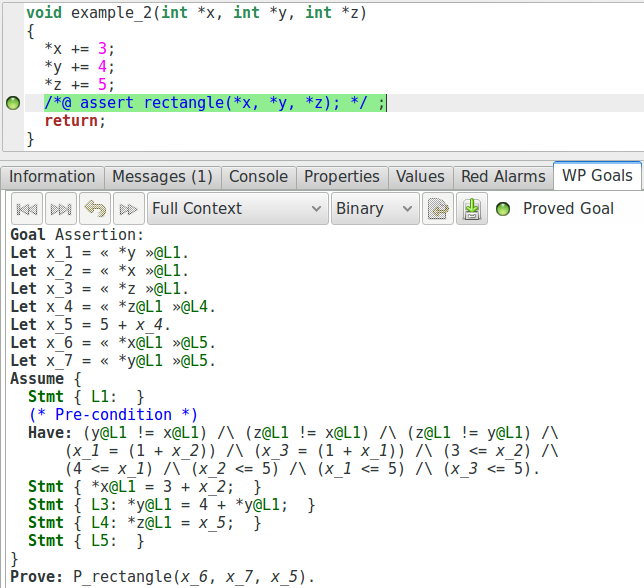
Ici, le solveur déroulera probablement le prédicat et vérifiera directement que la propriété qui y est définie est vraie.En effet, depuis l’obligation de preuve, il n’y a pas vraiment d’autre information qui pourrait nous amener à obtenir une preuve. Maintenant, ajoutons de l’information dans les annotations :

/*@
  requires \separated(x, y , z);
  requires 3 <= *x <= 5 ;
  requires 4 <= *y <= 5 ;
  requires *z <= 5 ;
  requires *x+2 == *y+1 == *z ;
*/
void example_3(int* x, int* y, int* z){
  //@ assert rectangle(2* (*x), 2* (*y), 2* (*z));
  //@ ghost L: ;
  
  *x += 3 ;
  *y += 4 ;
  *z += 5 ;

  //@ assert *x == \at(2* (*x), L) ;
  //@ assert *y == \at(2* (*y), L) ;
  //@ assert *z == \at(2* (*z), L);
  //@ assert rectangle(*x, *y, *z);
}

Nous prouvons d’abord que si nous multiplions par 2 chacune des valeurs, le prédicat est vrai pour les nouvelles valeurs. Le solveur prouvera d’abord la même propriété, bien sûr, mais ce n’est pas ce que nous voulons montrer ici. Nous ajoutons ensuite que chaque valeur a été multipliée par 2. Maintenant, nous pouvons regarder l’obligation de preuve générée pour la dernière assertion :

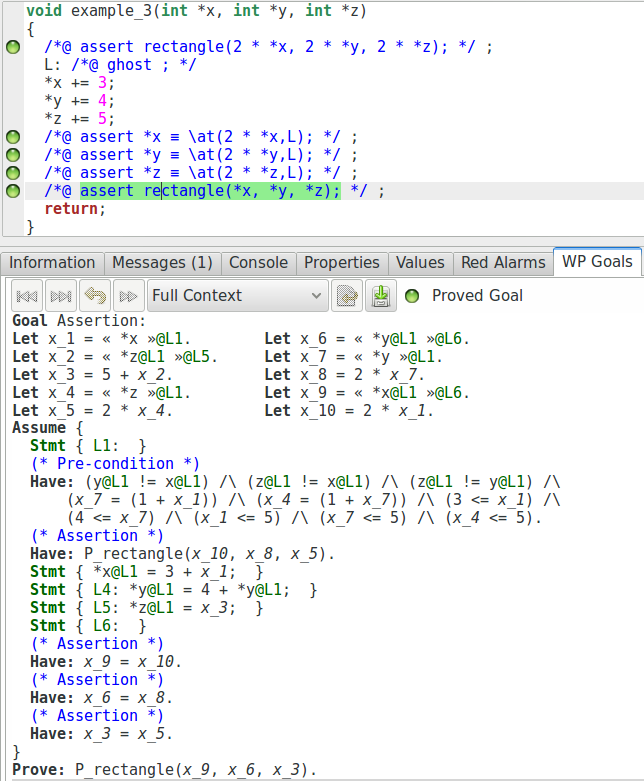
Alors que nous devons prouver exactement la même propriété qu’avant (avec un peu de renommage), nous pouvons voir que nous avons une autre manière de la prouver. En effet en combinant ces propriétés :

(* Assertion *)
Have: P_rectangle(x_10, x_8, x_5).
(* Assertion *)
Have: x_9 = x_10.
(* Assertion *)
Have: x_6 = x_8.
(* Assertion *)
Have: x_3 = x_5.

Il est facile de déduire :

Prove: P_rectangle(x_9, x_6, x_3).

En remplaçant simplement les valeurs x_9, x_6 et x_3. Donc le solveur pourrait utiliser ceci pour faire la preuve sans avoir à déplier le prédicat. Cependant, il ne le fera pas forcément : les solveurs SMT sont basés sur des méthodes heuristiques, nous pouvons juste leur fournir des propriétés et espérer qu’ils les utiliseront.

Ici la propriété est simple à prouver, donc il n’était pas vraiment nécessaire d’ajouter ces assertions (et donc de faire plus d’efforts pour faire la même chose). Cependant, dans d’autre cas, comme nous allons le voir maintenant, nous devons donner la bonne information au bon endroit de façon à ce que les prouveurs trouvent les informations dont ils ont besoin pour finir les preuves.

Déclencher les lemmes

Nous utilisons souvent des assertions pour exprimer des propriétés qui correspondent aux prémisses d’un lemme ou à ses conclusions. En faisant cela, nous maximisons les chances que les prouveurs automatiques « reconnaissent » que ce que nous avons écrit correspond à un lemme en particulier et qu’il devrait l’utiliser.

Illustrons cela avec l’exemple suivant. Nous utilisons des axiomes et non des lemmes parce qu’ils sont considérés de la même manière par WP lorsque nous nous intéressons à la preuve d’une propriété qui en dépend. Regardons d’abord notre définition axiomatique. Nous définissons deux prédicats P et Q à propos d’une position mémoire particulière x. Nous avons deux axiomes : ax_1 qui énonce que si P(x) est vraie, alors Q(x) est vraie, et un second axiome ax_2 qui énonce que si la position mémoire pointée ne change pas entre deux labels (ce que l’on représente par le prédicat eq) et que P(x) est vraie pour le premier label, alors elle est vraie pour le second.

/*@
  predicate eq{L1, L2}(int* x) =
    \at(*x, L1) == \at(*x, L2) ;
*/

/*@
  axiomatic Ax {
    predicate P(int* x) reads *x ;
    predicate Q(int* x) reads *x ;
    axiom ax_1: \forall int* x ; P(x) ==> Q(x);
    axiom ax_2{L1, L2}: 
      \forall int* x ; eq{L1, L2}(x) ==> P{L1}(x) ==> P{L2}(x);
  }
*/

Et nous voulons prouver le programme suivant :

/*@ assigns *x ; */
void g(int* x);

/*@
  requires \separated(x, y);
  requires P(x) ;
  ensures  Q(x) ;
*/
void example(int* x, int* y){
  g(y); 
}

Cependant, nous pouvons voir que la preuve échoue sur l’obligation de preuve suivante (nous avons, à nouveau, retiré les éléments qui ne sont pas intéressants pour notre explication) :

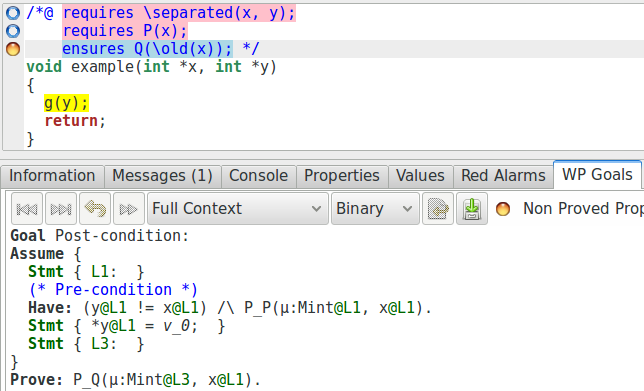
D’après cela, notre prouver automatique semble incapable d’utiliser l’un des axiomes de notre définition : soit il ne peut pas montrer qu’après l’appel g(y), P(x) est toujours vraie, soit il le peut, et dans ce cas, cela veut dire qu’il n’arrive pas à montrer que cela implique Q(x). Essayons donc d’ajouter une assertion pour vérifier qu’il arrive à montrer P(x) après l’appel :

/*@
  requires \separated(x, y);
  requires P(x) ;
  ensures  Q(x) ;
*/
void example(int* x, int* y){
  g(y);
  //@ assert P(x);
}

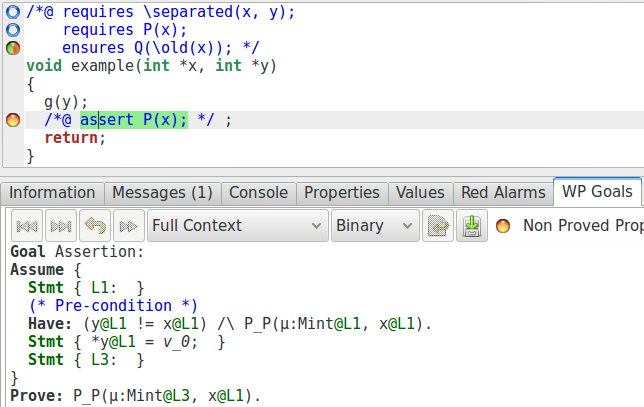
Il semble que malgré le fait qu’il est clair que *x n’a pas changé pendant l’appel g(y), et donc que eq{Pre, Here}(x) est vraie après l’appel, puisque la propriété n’est pas directement fournie dans notre obligation de preuve, le prouveur automatique n’utilise pas l’axiome ax_2 correspondant. Fournissons donc cette information au prouveur automatique :

/*@
  requires \separated(x, y);
  requires P(x) ;
  ensures  Q(x) ;
*/
void example(int* x, int* y){
  g(y);
  //@ assert eq{Pre, Here}(x); 
}

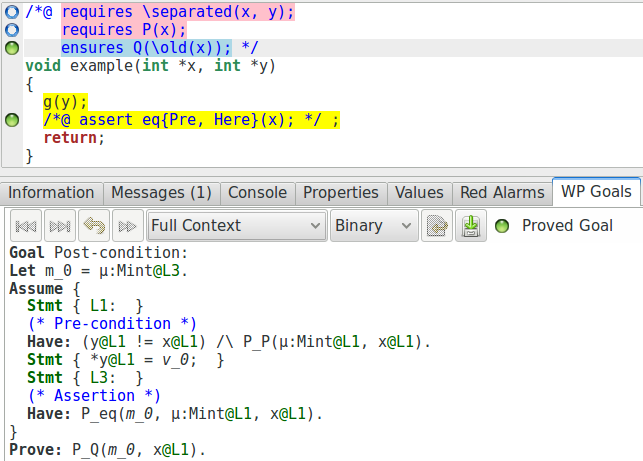
Maintenant, tout est prouvé. Si nous regardons l’obligation de preuve générée, nous pouvons voir que l’information nécessaire est bien fournie, ce qui permet au prouveur automatique d’en faire usage :

Un exemple plus complexe : du tri à nouveau

Travaillons maintenant avec un exemple plus complexe utilisant une définition axiomatique réelle. Cette fois, nous nous intéresserons à montrer la correction d’un tri par insertion :


#include <stddef.h>
#include <limits.h>

void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;

  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }
  a[i] = value ;
}

void insertion_sort(int* a, size_t beg, size_t end){
  for(size_t i = beg+1; i < end; ++i)
    insert(a, beg, i);
}

La fonction insertion_sort visite chaque valeur, du début du tableau jusqu’à la fin. Pour chaque valeur $v$ , elle est insérée (en utilisant la fonction insert) à la bonne place dans la plage des valeurs déjà triées (et qui se trouvent dans le début du tableau), en décalant les éléments jusqu’à rencontrer un élément qui est plus petit que $v$ , ou le début du tableau.

Nous voulons prouver la même postcondition que ce que nous avons déjà prouvé pour le tri par sélection, c’est-à-dire que nous voulons créer une permutation triée des valeurs originales. À nouveau, chaque itération de la boucle doit assurer que la nouvelle configuration obtenue est une permutation des valeurs originales, et que la plage de valeurs allant du début à la cellule actuellement visitée est triée. Toutes ces propriétés sont garanties par la fonction insert. Si l’on regarde cette fonction de plus près, nous voyons qu’elle enregistre la valeur à insérer (qui se trouve à la fin de la plage de valeurs) dans une variable value, et en commençant à la fin de la plage, décale itérativement les valeurs rencontrées jusqu’à rencontrer une valeur plus petite que la valeur à insérer ou la première cellule du tableau, et insère ensuite la valeur.

Tout d’abord, fournissons un contrat et un invariant pour la fonction de tri par insertion. Le contrat est équivalent à celui que nous avions fourni pour le tri par sélection. Notons cependant que l’invariant est plus faible : nous n’avons pas besoin que les valeurs restant à trier soient plus grandes que les valeurs déjà visitées : nous insérons chaque valeur à la bonne position.

/*@
  requires beg < end && \valid(a + (beg .. end-1));
  assigns a[beg .. end-1];
  ensures sorted(a, beg, end);
  ensures permutation{Pre, Post}(a,beg,end);
*/
void insertion_sort(int* a, size_t beg, size_t end){
  /*@
    loop invariant beg+1 <= i <= end ;
    loop invariant sorted(a, beg, i) ;
    loop invariant permutation{Pre, Here}(a,beg,end);
    loop assigns a[beg .. end-1], i ;
    loop variant end-i ;
  */
  for(size_t i = beg+1; i < end; ++i) {
    insert(a, beg, i);
  }
}

Maintenant, nous pouvons fournir un contrat à la fonction d’insertion. La fonction requiert que la plage de valeurs considérée soit triée du début jusqu’à l’avant-dernière valeur. En échange, elle doit garantir que la plage finale est triée et est une permutation des valeurs originales :

/*@
  requires beg < last < UINT_MAX && \valid(a + (beg .. last));
  requires sorted(a, beg, last) ;
  assigns a[ beg .. last ] ;
  
  ensures permutation{Pre, Post}(a, beg, last+1);
  ensures sorted(a, beg, last+1) ;
*/
void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;

  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }
  a[i] = value ;
}

Ensuite, nous devons fournir un invariant utilisable pour expliquer le comportement de la boucle de la fonction insert. Cette fois, nous pouvons voir qu’avec notre précédente définition de la notion de permutation, nous sommes un peu embêtés. En effet, notre définition inductive de la permutation spécifie trois cas : une plage de valeur est une permutation d’elle-même, ou deux (et seulement deux) valeurs ont été changées, ou finalement la permutation d’une permutation est une permutation. Mais aucun de ces cas ne peut être appliqué à notre fonction d’insertion puisque la plage obtenue ne l’est pas par une succession d’échanges de valeurs, et les deux autres cas ne peuvent évidemment pas s’appliquer ici.

Nous avons donc besoin d’une meilleure définition pour notre permutation. Nous pouvons constater que ce dont nous avons vraiment besoin, c’est une manière de dire « chaque valeur qui était dans le tableau est toujours dans le tableau et si plusieurs valeurs étaient équivalentes, le nombre d’occurrences de ces valeurs ne change pas ». En fait, nous n’avons besoin que de la dernière partie de cette définition pour exprimer notre permutation. Une permutation est une plage de valeurs telles que pour toute valeur, le nombre d’occurrences de cette valeur dans cette plage ne change pas d’un point de programme à un autre :

/*@
  predicate permutation{L1, L2}(int* in, integer from, integer to) =
    \forall int v ; l_occurrences_of{L1}(v, in, from, to) ==
                    l_occurrences_of{L2}(v, in, from, to) ;
*/

En partant de cette définition, nous sommes capables de fournir des lemmes qui nous permettront de raisonner efficacement à propos des permutations, à supposer que certaines propriétés sont vraies à propos du tableau entre deux points de programme. Par exemple, nous pourrions définir le cas Swap de notre définition inductive précédente en utilisant un lemme. C’est bien entendu aussi le cas pour notre plage de valeur « décalée ».

Déterminons quels sont les lemmes requis en considérant d’abord la fonction insert_sort. La seule propriété non-prouvée est l’invariant qui exprime que le tableau est une permutation du tableau original. Comment pouvons-nous le déduire ? (Nous nous intéresserons aux preuves de ces lemmes plus tard).

Nous pouvons observer deux faits : la première plage du tableau (de beg à i+1) est une permutation de la même plage au début de l’itération (par le contrat de la fonction insert). La seconde partie (de i+1 à end) est inchangée, donc c’est aussi une permutation. Essayons d’utiliser quelques assertions pour voir parmi ces propriétés ce qui peut être prouvé et ce qui ne peut pas l’être. Tandis que la première propriété est bien prouvée, nous pouvons voir que la seconde ne l’est pas :

  /*@
    loop invariant beg+1 <= i <= end ;
    loop invariant sorted(a, beg, i) ;
    loop invariant permutation{Pre, Here}(a,beg,end);
    loop assigns a[beg .. end-1], i ;
    loop variant end-i ;
  */
  for(size_t i = beg+1; i < end; ++i) {
    //@ ghost L:
    insert(a, beg, i);
    //@ assert permutation{L, Here}(a, beg, i+1); // PROVED
    //@ assert permutation{L, Here}(a, i+1, end); // NOT PROVED
  }

Nous avons donc besoin d’un premier lemme pour cette propriété. Définissons deux prédicats shifted et unchanged, le second étant utilisé pour définir le premier (nous verrons pourquoi un peu plus tard) et exprimer qu’une plage inchangée est une permutation :

/*@
  predicate shifted{L1, L2}(integer s, int* a, integer beg, integer end) =
    \forall integer k ; beg <= k < end ==> \at(a[k], L1) == \at(a[s+k], L2) ;
*/
/*@
  predicate unchanged{L1, L2}(int* a, integer beg, integer end) =
    shifted{L1, L2}(0, a, beg, end);
*/
/*@ lemma unchanged_is_permutation{L1, L2}:
  \forall int* a, integer beg, integer end ;
    unchanged{L1, L2}(a, beg, end) ==> permutation{L1, L2}(a, beg, end) ;
*/

Maintenant, nous pouvons vérifier que ces deux sous-tableaux sont des permutations, nous faisons cela en ajoutant une assertion qui montre que la plage allant de i+1 à end est inchangée, afin de déclencher l’usage de notre lemme unchanged_is_permutation.

  /*@
    loop invariant beg+1 <= i <= end ;
    loop invariant sorted(a, beg, i) ;
    loop invariant permutation{Pre, Here}(a,beg,end);
    loop assigns a[beg .. end-1], i ;
    loop variant end-i ;
  */
  for(size_t i = beg+1; i < end; ++i) {
    //@ ghost L:
    insert(a, beg, i);
    //@ assert permutation{L, Here}(a, beg, i+1);
    //@ assert unchanged{L, Here}(a, i+1, end) ;
    //@ assert permutation{L, Here}(a, i+1, end) ;
  }

Comme ces deux sous-parties du tableau sont des permutations, le tableau global est une permutation des valeurs initialement présentes au début de l’itération. Cependant, cela n’est pas prouvé directement, nous ajoutons donc aussi un lemme pour cela :

/*@ lemma union_permutation{L1, L2}:
  \forall int* a, integer beg, split, end, int v ;
    beg <= split <= end ==>
    permutation{L1, L2}(a, beg, split) ==> 
    permutation{L1, L2}(a, split, end) ==>
      permutation{L1, L2}(a, beg, end) ;
*/

Maintenant, nous pouvons déduire qu’une itération de la boucle produit une permutation en ajoutant cette conclusion comme une assertion :

    //@ ghost L: ;
    insert(a, beg, i);
    //@ assert permutation{L, Here}(a, beg, i+1);
    //@ assert unchanged{L, Here}(a, i+1, end);
    //@ assert permutation{L, Here}(a, i+1, end);
    //@ assert permutation{L, Here}(a, beg, end); // PROVED

Finalement, nous devons ajouter une information supplémentaire, la permutation d’une permutation est aussi une permutation. Cette fois, nous n’avons pas besoin d’une assertion supplémentaire. Le contexte contient :

permutation{Pre, L}(a, beg, end) (invariant)
permutation{L, Here}(a, beg, end) (assertion)

qui est suffisant pour conclure permutation{Pre, Here}(a, beg, end) à la fin du bloc de la boucle en utilisant le lemme suivant :

/*@ lemma transitive_permutation{L1, L2, L3}:
  \forall int* a, integer beg, integer end ;
    permutation{L1, L2}(a, beg, end) ==> 
    permutation{L2, L3}(a, beg, end) ==> 
      permutation{L1, L3}(a, beg, end) ;
*/

Maintenant, nous pouvons regarder de plus près notre fonction d’insertion en nous intéressant d’abord à comment obtenir la connaissance que la fonction produit une permutation.

Elle décale les différents éléments vers la gauche jusqu’à rencontrer le début du tableau ou un élément plus petit que l’élément à insérer qui est initialement à la fin de la plage de valeur et inséré à la position ainsi atteinte. Les cellules du début du tableau jusqu’à la position d’insertion restent inchangées, c’est donc une permutation. Nous avons un lemme pour cela, mais nous devons ajouter cette connaissance que le début du tableau ne change pas comme un invariant de la boucle pour pouvoir déclencher le lemme après celle-ci. La seconde partie du tableau est une permutation parce que nous faisons « tourner » les éléments, nous avons besoin d’un lemme pour exprimer cela et d’indiquer dans l’invariant de boucle que les éléments sont décalés par la boucle. Finalement, l’union de deux permutations est une permutation et nous avons déjà un lemme pour cela.

Tout d’abord, donnons un invariant pour la permutation :

nous fournissons les bornes de i,
nous indiquons que la première partie du tableau est inchangée,
nous indiquons que la seconde partie est décalée vers la gauche.

et nous ajoutons quelques assertions pour vérifier quelques propriétés d’intérêt :

d’abord, pour déclencher unchanged_permutation, nous plaçons une première assertion pour énoncer que la première partie du tableau est inchangée, ce qui nous permet de prouver que …
la seconde assertion, qui nous dit que la première partie du tableau est une permutation de l’originale, et que l’on utilise en combinaison avec …
la troisième assertion qui nous dit que la seconde partie du tableau est une permutation de l’originale (qui nous permet de déclencher l’usage de union_permutation et de prouver la postcondition).

  /*@
    loop invariant beg <= i <= last ;
    loop invariant \forall integer k ; beg <= k <= i    ==> a[k] == \at(a[k], Pre) ;
    loop invariant \forall integer k ; i+1 <= k <= last ==> a[k] == \at(a[k-1], Pre) ;

    loop assigns i, a[beg .. last] ;
    loop variant i ;
  */
  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }

  a[i] = value ;

  //@ assert unchanged{Pre, Here}(a, beg, i) ;   // PROVED
  //@ assert permutation{Pre, Here}(a, beg, i) ; // PROVED

  //@ assert rotate_left{Pre, Here}(a, i, last+1) ; //PROVED
  //@ assert permutation{Pre, Here}(a, i, last+1) ; // NOT PROVED

Pour la dernière assertion, nous avons besoin d’un lemme à propos de la rotation des éléments :

/*@
  predicate rotate_left{L1, L2}(int* a, integer beg, integer end) =
    beg < end && \at(a[beg], L2) == \at(a[end-1], L1) &&
    shifted{L1, L2}(1, a, beg, end - 1) ;
*/
/*@ lemma rotate_left_is_permutation{L1, L2}:
  \forall int* a, integer beg, integer end ;
    rotate_left{L1, L2}(a, beg, end) ==> permutation{L1, L2}(a, beg, end) ;
*/

Nous devons également aider un peu les prouveurs automatiques pour montrer que l’ensemble des valeurs est trié après l’insertion. Pour cela, nous fournissons un nouvel invariant pour montrer que les valeurs « décalées » sont plus grandes que la valeur à insérer. Puis, nous ajoutons également des assertions pour montrer que le tableau est trié avant l’insertion, et que toutes les valeurs avant la cellule où nous insérons sont plus petites que la valeur insérée, et que la plage est en conséquence triée après l’insertion. Cela nous amène à la fonction insert complètement annotée suivante :

/*@
  requires beg < last < UINT_MAX && \valid(a + (beg .. last));
  requires sorted(a, beg, last) ;
  assigns a[ beg .. last ] ;
  
  ensures permutation{Pre, Post}(a, beg, last+1);
  ensures sorted(a, beg, last+1) ;
*/
void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;

  /*@
    loop invariant beg <= i <= last ;
    loop invariant \forall integer k ; i <= k < last ==> a[k] > value ;
    loop invariant \forall integer k ; beg <= k <= i    ==> a[k] == \at(a[k], Pre) ;
    loop invariant \forall integer k ; i+1 <= k <= last ==> a[k] == \at(a[k-1], Pre) ;
    loop assigns i, a[beg .. last] ;
    loop variant i ;
  */
  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }
  //@ assert sorted(a, beg, last+1) ;
  //@ assert \forall integer k ; beg <= k < i ==> a[k] <= value ;
  a[i] = value ;
  //@ assert sorted(a, beg, last+1) ;

  //@ assert unchanged{Pre, Here}(a, beg, i) ;
  //@ assert permutation{Pre, Here}(a, beg, i) ;

  //@ assert rotate_left{Pre, Here}(a, i, last+1) ;
  //@ assert permutation{Pre, Here}(a, i, last+1) ;
}

En tout, nous avons six lemmes à prouver :

l_occurrences_union,
shifted_maintains_occ,
unchanged_is_permutation,
rotate_left_is_permutation,
union_permutation,
transitive_permutation.

Tandis que les preuves Coq de ces lemmes sont en dehors des préoccupations de ce tutoriel (et nous verrons plus tard que dans le cas particulier de cette preuve nous pouvons nous en débarrasser), donnons quelques indications pour obtenir une preuve de ces lemmes (notons que les scripts Coq de ces preuves sont disponibles sur le GitHub de ce tutoriel).

Pour prouver l_occurrences_union, nous raisonnons par induction sur la taille de la seconde partie du tableau. Le cas de base est trivial : si la taille est 0, nous avons immédiatement l’égalité puisque split == to. Maintenant, nous devons prouver que si l’égalité est vraie pour une plage de taille $i$ , elle est vraie pour une plage de taille $i+1$ . Puisque nous savons que c’est le cas jusqu’à $i$ par hypothèse d’induction, nous analysons simplement les différents cas pour le dernier élément de la plage (au rang $i$ ) : soit cet élément est celui que nous comptons, soit il ne l’est pas. Quoi qu’il en soit, cela ajoute la même valeur des deux côtés de l’égalité.

Pour shifted_maintains_occ, nous raisonnons par induction sur la plage complète. Le premier cas est trivial (la plage est vide). Pour le cas d’induction, nous avons juste à montrer que la valeur ajoutée a été décalée, et qu’elle est donc la même.

La propriété unchanged_is_permutation peut être prouvée par les solveurs SMT grâce au fait que nous avons exprimé unchanged en utilisant shifted, le prouveur peut donc directement instancier le lemme précédent. Si ce n’est pas le cas, la preuve peut être réalisée en instanciant shifted_maintains_occ avec la valeur 0 pour la propriété de décalage.

Pour prouver rotate_left_is_permutation, nous séparons la plage pour L1 en deux sous-plages beg .. beg+1 et beg+1 .. end et la plage pour L2 en deux sous-plages beg .. end-1 et end-1 .. end en utilisant la propriété l_occurrences_union. Nous montrons que le nombre d’occurrences dans beg+1 .. end pour L1 et beg .. end-1 pour L2 n’a pas changé grâce à shifted_maintains_occ et que le nombre d’occurrences dans beg .. beg+1 pour L1 et end-1 .. end pour L2 est le même en analysant par cas (et en utilisant le fait que la valeur correspondante est la même).

Pour prouver union_permutation, nous instancions le lemme l_occurrences_union. Finalement, le lemme transitive_permutation est prouvée automatiquement par transitivité de l’égalité.

Comment utiliser correctement les assertions ?

Il n’y a pas de guide précis à propos de quand utiliser des assertions ou non. La plupart du temps nous les utilisons d’abord pour comprendre pourquoi certaines preuves échouent en exprimant des propriétés dont nous pensons qu’elles sont vraies à un point particulier de programme. De plus, il n’est pas rare que les obligations de preuve soient longues ou un peu complexes à lire directement. Bien utiliser les assertion nécessite que l’on garde en tête les lemmes déjà exprimés pour savoir quelle assertion utiliser pour déclencher l’usage d’un lemme nous amenant à la propriété voulue. S’il n’y a pas de tel lemme, par exemple parce que la preuve de la propriété voulue nécessite un raisonnement par induction à propos d’une propriété ou d’une valeur, nous avons probablement besoin d’ajouter un nouveau lemme.

Avec un peu d’expérience, l’utilisation des assertions et des lemmes devient de plus en plus naturelle. Cependant, il est important de garder en tête qu’il est facile d’abuser de cela. Plus nous ajoutons de lemmes et d’assertions, plus notre contexte de preuve est riche et est susceptible de contenir les informations nécessaires à la preuve. Cependant, il y a aussi un risque d’ajouter trop d’information de telle manière à ce que le contexte de preuve finisse par contenir des informations inutiles qui polluent le contexte de preuve, rendant le travail des solveurs SMT plus difficile. Nous devons donc essayer de trouver le bon compromis.

Exercices

Comprendre le contexte de preuve

Dans la fonction suivante, la dernière assertion est prouvée automatiquement par le solveur SMT, probablement en dépliant le prédicat pour prouver directement la propriété. En utilisant des assertions, fournir une nouvelle manière de prouver la dernière propriété. Dans le contexte de preuve, trouver les propriétés générées qui peuvent amener à une autre preuve de l’assertion et expliquer comment :

/*@
  predicate rectangle{L}(integer c1, integer c2, integer h) =
    c1 * c1 + c2 * c2 == h * h ;
*/

/*@
  requires \separated(x, y , z);
  requires 3 <= *x <= 5 ;
  requires 3 <= *y <= 5 ;
  requires 2 <= *z <= 5 ;
  requires *x+2 == *y+1 == *z ;
*/
void exercise(int* x, int* y, int* z){
  *x += 2 * (*x) ;
  *y += *y ;
  *y += (*y / 2);
  *z = 3 * (*z) ;
  //@ assert rectangle(*x, *y, *z);
}

Déclencher les lemmes

Dans le programme suivant, WP échoue à prouver que la postcondition de la fonction g est vérifiée. Ajouter la bonne assertion, au bon endroit, de façon à ce que la preuve réussisse.

/*@
  axiomatic Ax {
    predicate X{L1, L2}(int* p, integer l)
        reads \at(p[0 .. l-1], L1), \at(p[0 .. l-1], L2) ;
    predicate Y{L1, L2}(int* p, integer l)
        reads \at(p[0 .. l-1], L1), \at(p[0 .. l-1], L2) ;
    axiom Ax_axiom_XY {L1,L2}:
      \forall int* p, integer l, i ; 0 <= i <= l ==> X{L1, L2}(p, i) ==> Y{L1, L2}(p, l) ;
    axiom transitive{L1,L2,L3}:
      \forall int* p, integer l ; Y{L1,L2}(p, l) ==> Y{L2,L3}(p, l) ==> Y{L1,L3}(p, l);
  }
*/

/*@
  assigns p[0 .. l-1] ;
  ensures X{Pre, Post}(p, l) ;
*/
void f(int* p, unsigned l);

/*@
  ensures Y{Pre,Post}(p, l);
*/
void g(int* p, unsigned l){
  f(p, l) ;
  f(p, l) ;
}

Déclencher les lemmes sous condition

Dans le programme suivant, WP échoue à prouver que la postcondition de la fonction example est vérifiée. Cependant, nous pouvons noter que la fonction g assure indirectement que la valeur pointée est soit augmentée soit diminuée. Ajouter deux assertions qui montrent que le prédicat est vérifié en fonction de la valeur de *x.

/*@
  predicate dec{L1, L2}(int* x) =
    \at(*x, L1) > \at(*x, L2) ;
  predicate inc{L1, L2}(int* x) =
    \at(*x, L1) < \at(*x, L2) ;
*/

/*@
  axiomatic Ax {
    predicate P(int* x) reads *x ;
    predicate Q(int* x) reads *x ;
    axiom ax_1: \forall int* x ; P(x) ==> Q(x);
    axiom ax_2{L1, L2}: 
      \forall int* x ; dec{L1, L2}(x) ==> P{L1}(x) ==> P{L2}(x);
    axiom ax_3{L1, L2}: 
      \forall int* x ; inc{L1, L2}(x) ==> P{L1}(x) ==> P{L2}(x);
  }
*/

/*@
  assigns *x ; 
  behavior b_1:
    assumes *x < 0 ;
    ensures *x >= 0 ;
  behavior b_2:
    assumes *x >= 0 ;
    ensures *x < 0 ;
  complete behaviors ;
  disjoint behaviors ;
*/
void g(int* x);

/*@
  requires P(x) ;
  ensures  Q(x) ;
*/
void example(int* x){
  g(x);
}

Les assertions devraient ressembler à :

//@ assert *x ... ==> ... ;
//@ assert *x ... ==> ... ;

Une autre manière d’ajouter de l’information au contexte est d’utiliser du code fantôme. Par exemple, la valeur de vérité d’une conditionnelle apparaît dans le contexte d’une obligation de preuve. Modifier les annotations pour que le code ressemble à :

void example(int* x){
  g(x);
  /*@ ghost
   if ( ... ){
    /@ assert ... @/
   } else {
    /@ assert ... @/
   }
  */
}

Comparer l’obligation de preuve générée pour chaque assertion avec les précédentes.

Finalement, nous pouvons remarquer que « la valeur pointée a été augmentée ou diminuée » peut être exprimée en une seule assertion. Écrire l’annotation correspondante et recommencer la preuve.

Un exemple avec la somme

La fonction suivante incrémente de 1 la valeur d’une cellule du tableau, donc elle augmente aussi la valeur de la somme du contenu du tableau. Écrire un contrat pour la fonction qui exprime ce fait :

#include <stddef.h>

/*@
  axiomatic Sum_array{
    logic integer sum(int* array, integer begin, integer end) reads array[begin .. (end-1)];
    axiom empty: 
      \forall int* a, integer b, e; b >= e ==> sum(a,b,e) == 0;
    axiom range:
      \forall int* a, integer b, e; b < e ==> sum(a,b,e) == sum(a,b,e-1)+a[e-1];
  }
*/

/*@
  predicate unchanged{L1, L2}(int* array, integer begin, integer end) =
    \forall integer i ; begin <= i < end ==> \at(array[i], L1) == \at(array[i], L2) ;
*/

/*@
  lemma sum_separable:
    \forall int* array, integer begin, split, end ;
      begin <= split <= end ==> sum(array, begin, end) == ... ?
  lemma unchanged_sum{L1, L2}:
    \forall int* array, integer begin, end ;
      unchanged{L1, L2}(array, begin, end) ==> ... ?
*/

void inc_cell(int* array, size_t len, size_t i){
  array[i]++ ;
}

Pour prouver que cette fonction remplit son contrat, nous avons besoin de fournir des assertions qui guideront la preuve. Plus précisément, nous devons montrer que puisque toutes les valeurs avant la cellule modifiée n’ont pas été modifiées, la somme n’a pas été modifiée pour cette partie du tableau, et de même pour les cellules qui suivent la cellule modifiée.

Nous avons donc besoin de deux lemmes :

sum_separable doit exprimer que nous pouvons séparer le tableau en deux sous parties, compter dans chaque partie et sommer les résultats pour obtenir la somme totale,
unchanged_sum devrait exprimer que si une plage dans un tableau n’a pas changé entre deux labels, la somme du contenu est la même.

Compléter les code des lemmes et utiliser des assertions pour assurer qu’ils sont utilisés pour compléter la preuve. Nous ne demandons par la preuve des lemmes, les preuves Coq sont disponibles sur le GitHub de ce tutoriel.

Plus de code fantôme, fonctions lemmes et macros lemmes

Les assertions nous permettent de donner des indices au générateur d’obligation de preuves pour les solveurs SMT obtiennent assez d’information pour produire la preuve dont nous avons besoin. Cependant, il est parfois difficile d’écrire une assertion qui créera exactement la propriété dont le solveur SMT a besoin pour déclencher le bon lemme (par exemple, puisque le générateur effectue des optimisations sur les obligations de preuve, ils peuvent légèrement la modifier, ainsi que le contexte de preuve). De plus, nous reposons sur des lemmes qui ont souvent besoin d’être prouvés en Coq, et pour cela nous avons besoin d’apprendre Coq.

Dans cette section, nous verrons quelques techniques qui peuvent être utilisées pour rendre tout cela plus prédictible et nous éviter d’utiliser l’assistant de preuve Coq. Tandis que ces techniques ne peuvent pas toujours être utilisées (et nous expliquerons quand cela n’est pas applicable), elles sont généralement efficaces pour obtenir de la preuve presque complètement automatiques. Cela repose sur l’usage de code fantôme.

Preuve par induction

Précédemment, nous avons mentionné que les solveurs SMT sont mauvais pour effectuer des preuves par induction (la plupart du temps), et c’est la raison pour laquelle nous avons souvent besoin d’exprimer des lemmes que nous prouvons avec l’assistant de preuve Coq qui nous permet de faire notre preuve par induction. Cependant, dans la section à propos des boucles, nous trouvons une sous-section nommée « Induction et invariant », où nous expliquons que pour prouver un invariant de boucle, nous procédons … par induction. L’auteur de ce tutoriel aurait-il honteusement menti au lecteur pendant tout ce temps ?

En fait non, et la raison est plutôt simple. Lorsque nous prouvons un invariant de boucle par induction en utilisant des solveurs SMT, ils n’ont pas besoin d’effectuer le raisonnement par induction eux-mêmes. Le travail qui consiste à séparer la preuve en deux sous-preuves, la première pour l’établissement de l’invariant (le cas de base de la preuve), et la seconde pour la préservation (le cas d’induction) est effectué par le générateur d’obligations de preuve. Par conséquent, quand les obligations de preuves sont transmises aux solveurs SMT, ce travail n’est plus nécessaire.

Comment pouvons-nous exploiter cette idée ? Nous avons expliqué précédemment que le code fantôme peut être utilisé pour fournir plus d’information que ce qui est explicitement fourni par le code source. Pour cela, nous ajoutons du code fantôme (et possiblement des annotations à propos de ce code) qui nous permet de déduire plus de propriétés. Illustrons cela avec un exemple simple. Dans un exercice précédent, nous voulions prouver l’appel de fonction suivant (nous avons exclus la postcondition pour raccourcir l’exemple) :


#include <stddef.h>
#include <limits.h>

/*@ predicate sorted(int* arr, integer end) =
      \forall integer i, j ; 0 <= i <= j < end ==> arr[i] <= arr[j] ;
    predicate element_level_sorted(int* array, integer end) =
      \forall integer i ; 0 <= i < end-1 ==> array[i] <= array[i+1] ; 
*/

/*@ requires \valid_read(arr + (0 .. len-1));
    requires sorted(arr, len) ;
*/
size_t bsearch(int* arr, size_t len, int value);

/*@ requires \valid_read(arr + (0 .. len-1));
    requires element_level_sorted(arr, len) ;
*/
unsigned bsearch_callee(int* arr, size_t len, int value){
  return bsearch(arr, len, value);
}

Pour cela, la solution que nous avions demandée dans l’exercice était de fournir un lemme qui énonce qui si la plage est « triée localement », au sens où chaque élément est supérieur ou égal à l’élément qui le précède, alors nous pouvons dire qu’elle est « globalement triée », c’est-à-dire que pour chaque paire d’indices $i$ et $j$ , si $i \leq j$ alors le $j^{ième}$ élément du tableau est supérieur ou égal au $i^{ième}$ élément. Donc, la précondition de la fonction pouvait être prouvée par les solveurs SMT, mais pas le lemme lui-même qui nécessite une preuve Coq. Est-ce que l’on ne pourrait pas faire quelque chose de mieux à ce sujet ?

La réponse est oui. Avant d’appeler la fonction, nous pouvons construire une preuve qui montre que puisque le tableau est trié localement, nous pouvons déduire qu’il est trié globalement (ce qui est simplement la preuve du lemme dont nous aurions besoin). Pour écrire cette preuve à la main, nous procéderions par induction sur la taille de la plage. Nous avons deux cas. D’abord si la plage est vide, la propriété est trivialement vraie. Ensuite, supposons qu’une plage donnée de taille $i$ avec $i < length$ ( $length$ étant la taille de la plage complète) est globalement triée et montrons que si c’est le cas, alors la plage de taille $i+1$ est triée. C’est facile parce que, d’après notre précondition, nous savons que le $i^{ième}$ élément est supérieur ou égal au $(i-1)^{ième}$ élément, qui est lui-même plus grand que tous les éléments qui précède.

Comment pouvons-nous traduire cela en code fantôme ? Nous écrivons une boucle qui va de $0$ (notre cas de base) à la fin len et nous fournissons un invariant montrant que le tableau est globalement trié depuis $0$ jusqu’à la cellule actuellement visitée. Nous ajoutons également une assertion pour aider le prouveur (qui nous dit que l’élément courant est plus grand que les éléments qui précèdent) :

/*@ requires \valid_read(arr + (0 .. len-1));
    requires element_level_sorted(arr, len) ;
*/
unsigned bsearch_callee(int* arr, size_t len, int value){
  /*@ ghost
    /@
      loop invariant 0 <= i <= len ;
      loop invariant sorted(arr, i) ;
      loop assigns i ;
      loop variant len-i ;
    @/
    for(size_t i = 0 ; i < len ; ++i){
      /@ assert 0 < i ==> arr[i-1] <= arr[i] ; @/      
    }
  */
  return bsearch(arr, len, value);
}

Nous pouvons voir que toutes les obligations de preuve sont facilement vérifiées par les solveurs SMT, sans que cela ne nécessite d’écrire une preuve Coq ou un lemme. Les obligations de preuve respectivement créées pour l’établissement et la préservation de l’invariant correspondent aux deux cas que nous avions besoin dans notre preuve par induction :

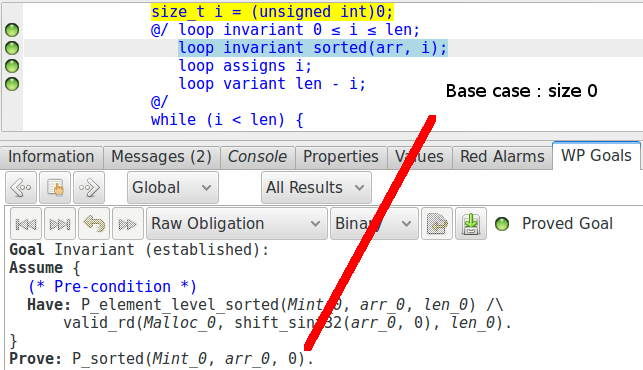
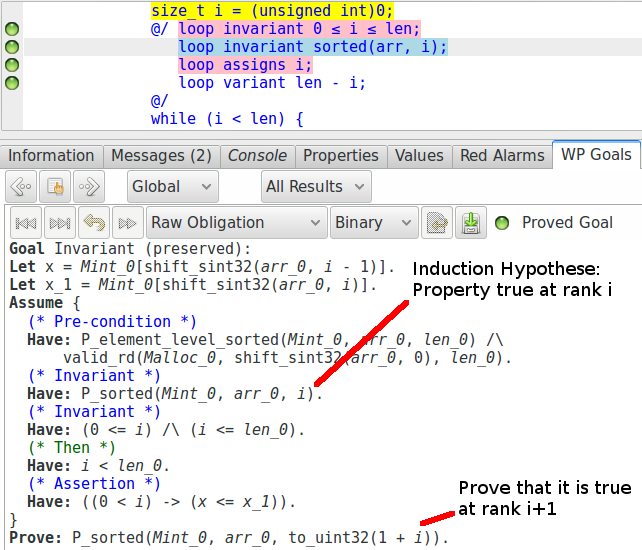
Ce type de code est appelé un « proof carrying code » : nous avons écrit un code et les annotations qui amènent la preuve d’une propriété que nous voulons vérifier.

Notons qu’ici, puisque nous devons écrire beaucoup de code fantôme, cela augmente notre risque d’introduction d’une erreur qui changerait les propriétés du code vérifié. Nous devons donc impérativement nous assurer que le code fantôme que nous avons écrit termine et qu’il ne contient pas d’erreurs à l’exécution (grâce au plugin RTE) pour avoir confiance dans notre vérification.

Dans cet exemple, nous avons directement écrit le code fantôme comme annotation du programme, cela signifie que si nous avons un autre appel comme celui-ci quelque part dans le code avec une précondition similaire, nous aurions à le faire à nouveau. Rendons cela plus simple et modulaire avec des « fonctions lemmes » (lemma functions).

Fonction lemme

Le principe des « fonctions lemmes » est le même que celui des lemmes : à partir de certaines prémisses, nous voulons arriver à une conclusion particulière. Et une fois que c’est fait, nous voulons les utiliser à d’autres endroits pour directement déduire la conclusion depuis les prémisses sans avoir à faire la preuve à nouveau, en instanciant les valeurs nécessaires.

La manière de faire cela est d’utiliser une fonction, en utilisant les clauses requires pour exprimer les prémisses du lemme, et les clauses ensures pour exprimer la conclusion du lemme. Les variables quantifiées universellement peuvent rester quantifiées ou correspondre à un paramètre de la fonction. Plus précisément, si une variable est uniquement liée aux prémisses ou uniquement aux conclusions, elle peut rester une variable quantifiée, à supposer qu’il ne soit pas nécessaire de la lier à une variable du code de preuve (puisque qu’une variable quantifiée n’est pas visible depuis le code C). Si elle est liée aux prémisses et conclusions, elle doit être un paramètre de la fonction (puisqu’ACSL ne nous permet pas de quantifier une variable pour un contrat de fonction entier).

Considérons l’exemple suivant où nous n’utilisons pas (directement) de variable universellement quantifiée dans le contrat, avec notre précédent exemple à propos des valeurs triées. Depuis la propriété element_level_sorted(arr, len), nous voulons déduire sorted(arr, len). Le lemme correspondant pourrait être :

/*@
  lemma element_level_sorted_is_sorted:
    \forall int* arr, integer len ;
       element_level_sorted(arr, len) ==> sorted(arr, len) ;
*/

Écrivons donc une fonction qui prend deux paramètres, arr et len, et requiert que le tableau soit trié localement et assure qu’il est trié globalement :

/*@ ghost
  /@
    requires element_level_sorted(arr, len) ;
    assigns  \nothing ;
    ensures  sorted(arr, len);
  @/
  void element_level_sorted_implies_sorted(int* arr, size_t len);
*/

Notons que cette fonction doit affecter \nothing. En effet, nous l’utilisons pour déduire des propriétés à propos du programme, dans du code fantôme, et donc elle ne devrait pas modifier le contenu du tableau, sinon le code fantôme modifierait le comportement du programme. Maintenant, produisons un corps pour cette fonction, le code qui nous amène la preuve que la conclusion est bien vérifiée en supposant que la précondition est vérifiée. Cela correspond au code que nous avons écrit précédemment pour prouver la précondition de l’appel de la fonction bsearch :

/*@ ghost
  /@
    requires element_level_sorted(arr, len) ;
    assigns  \nothing ;
    ensures  sorted(arr, len);
  @/
  void element_level_sorted_implies_sorted(int* arr, size_t len){
    /@
      loop invariant 0 <= i <= len ;
      loop invariant sorted(arr, i) ;
      loop assigns i ;
      loop variant len-i ;
    @/
    for(size_t i = 0 ; i < len ; ++i){
      /@ assert 0 < i ==> arr[i-1] <= arr[i] ; @/
    }
  }
*/

Avec cette boucle spécifiée, nous obtenons une preuve par induction que le lemme est vrai. Maintenant, nous pouvons utiliser cette fonction lemme en l’appelant tout simplement à l’endroit où nous avons besoin de faire cette déduction :

/*@ requires \valid_read(arr + (0 .. len-1));
    requires element_level_sorted(arr, len) ;
*/
unsigned bsearch_callee(int* arr, size_t len, int value){
  //@ ghost element_level_sorted_implies_sorted(arr, len) ;
  return bsearch(arr, len, value);
}

Ce qui nous demande d’établir la preuve que les prémisses sont établies grâce à la précondition de la fonction lemme (et qui est trivialement vraie, puisque nous l’obtenons de la précondition de bsearch_callee), et qui nous donne en retour la conclusion gratuitement puisque c’est la postcondition de la fonction lemme (et nous pouvons utiliser cette propriété comme précondition de l’appel à la fonction bsearch).

Comme nous l’avons expliqué, quand des variables universellement quantifiées sont liés à la fois aux prémisses et aux conclusions, elles doivent être des paramètres, c’est par exemple le cas ici pour les variables arr et len, tandis que pour les variables quantifiées dans les prédicats :

/*@ predicate sorted(int* arr, integer end) =
      \forall integer i, j ; 0 <= i <= j < end ==> arr[i] <= arr[j] ;
    predicate element_level_sorted(int* array, integer end) =
      \forall integer i ; 0 <= i < end-1 ==> array[i] <= array[i+1] ; 
*/

puisqu’elles ne sont respectivement liées qu’aux prémisses et aux conclusions restent universellement quantifiées (même si elles sont cachées dans les prédicats). Nous pourrions avoir écris le contrat comme ceci :

/*@
  /@
    requires \forall integer i ; 0 <= i < len-1 ==> arr[i] <= arr[i+1] ;
    assigns  \nothing ;
    ensures  \forall integer i, j ; 0 <= i <= j < len ==> arr[i] <= arr[j] ;
  @/
  void element_level_sorted_implies_sorted(int* arr, size_t len){
    /@
      loop invariant 0 <= i <= len ;
      loop invariant sorted(arr, i) ;
      loop assigns i ;
      loop variant len-i ;
    @/
    for(size_t i = 0 ; i < len ; ++i){
      /@ assert 0 < i ==> arr[i-1] <= arr[i] ; @/
    }
  }
*/

où nous voyons parfaitement que les variables sont toujours universellement quantifiées. Cependant, nous ne sommes pas obligés de les maintenir quantifiées universellement, et nous pourrions parfaitement les transformer en paramètres (en supposant que la conclusion que nous obtenir des prémisses a toujours du sens). Faisons par exemple cela pour les variables i et j de la conclusion :

/*@ ghost
  /@
    requires \forall integer i ; 0 <= i < len-1 ==> arr[i] <= arr[i+1] ;
    assigns  \nothing ;
    ensures  0 <= i <= j < len ==> arr[i] <= arr[j] ;
  @/
  void element_level_sorted_implies_greater(int* arr, size_t len, size_t i, size_t j){
    element_level_sorted_implies_sorted(arr, len);
  }
*/

Ce qui est tout à fait bon et nous pourrions par exemple utiliser cette fonction pour déduire des propriétés à propos du contenu du tableau. Notons qu’ici, nous utilisons un appel à la précédente fonction lemme pour rendre la preuve plus facile. Nous pouvons même aller plus loin en transférant la « prémisse de notre conclusion » en tant que prémisse d’un nouveau lemme :

/*@ ghost
  /@
    requires \forall integer i ; 0 <= i < len-1 ==> arr[i] <= arr[i+1] ;
    requires 0 <= i <= j < len ;
    assigns  \nothing ;
    ensures  arr[i] <= arr[j] ;
  @/
  void element_level_sorted_implies_greater_2(int* arr, size_t len, size_t i, size_t j){
    element_level_sorted_implies_sorted(arr, len);
  }
*/

Tous ces lemmes énoncent la même relation globale, la différence est liée à la quantité d’information requise pour les instancier (et par conséquent la précision de la propriété que nous obtenons en retour).

Finalement, présentons un dernier usage des fonctions lemmes. Dans tous les exemples précédents, nous avons considéré des variables universellement quantifiées. En fait, ce que nous avons dit précédemment est aussi applicable aux variables existentiellement quantifiées : si elles sont liées aux prémisses et aux conclusions, elles doivent être des paramètres, sinon elles peuvent donner lieu à des paramètres ou rester quantifiées. Cependant, à propos des variables existentiellement quantifiées, nous pouvons parfois aller plus loin en construisant une fonction qui nous fournit directement une valeur qui satisfait la propriété à propos de la variable existentiellement quantifiée.

Par exemple, considérons la définition axiomatique du comptage d’occurrences et imaginons qu’à un certain point de notre programme, nous voulons prouver l’assertion suivante à partir de la précondition :

/*@
  requires \valid(in + (0 .. len-1)) ;
  requires l_occurrences_of(v, in, 0, len) > 0 ;
*/
void foo(int v, int* in, size_t len){
  //@ assert \exists integer n ; 0 <= n < len && in[n] == v ;

  // ... code
}

Bien sûr, il existe un indice n tel que in[n] est v, sinon le nombre d’occurrences de cette valeur serait $0$ . Mais au lieu de prouver que cet index existe, montrons que nous pouvons trouver un index qui respecte les contraintes à propos de n en utilisant une fonction lemme qui le retourne :

/*@ ghost
  /@
    requires \valid(in + (0 .. len-1)) ;
    requires l_occurrences_of(v, in, 0, len) > 0 ;
    assigns \nothing ;
    ensures 0 <= \result < len && in[\result] == v ;
  @/
  size_t occ_not_zero_some_is_v(int v, int* in, size_t len){
    /@
      loop invariant 0 <= i < len ;
      loop invariant l_occurrences_of(v, in, 0, i) == 0 ;
      loop assigns i ;
      loop variant len-i ;
    @/
    for(size_t i = 0 ; i < len ; ++i){
      if(in[i] == v) return i ;
    }
    /@ assert \false ; @/
    return -1 ;
  }
*/

Si nous regardons seulement le corps de la fonction, il a deux comportements : soit il existe une cellule du tableau qui contient v et la fonction retourne son indice, ou ce n’est pas le cas, et dans ce cas la fonction retourne -1. Le premier comportement est facile à montrer, le retour correspondant à cette découverte n’est effectuée que dans une branche où l’on a trouvé une cellule qui correspond à la valeur recherchée.

Nous prouvons que le second comportement respecte la postcondition en montrant qu’il mène à une contradiction. S’il n’y a pas de cellule dont la valeur est v, alors le nombre d’occurrences de v est 0. C’est exprimé grâce au second invariant qui nous dit qu’aucun v n’a été rencontré depuis le début de la boucle, et donc le nombre d’occurrences est 0. Cependant, la précondition de la fonction nous énonce que le nombre d’occurrences est supérieur à 0, ce qui mène à une contradiction que nous modélisons par une assertion de faux (notons qu’elle n’est pas nécessaire, nous l’écrivons explicitement pour notre explication) ce qui signifie que ce chemin est infaisable.

Finalement, nous pouvons appeler cette fonction pour montrer qu’il existe un indice qui nous permet de valider notre assertion :

/*@
  requires \valid(in + (0 .. len-1)) ;
  requires l_occurrences_of(v, in, 0, len) > 0 ;
*/
void foo(int v, int* in, size_t len){
  //@ ghost size_t witness = occ_not_zero_some_is_v(v, in, len);
  //@ assert \exists integer n ; 0 <= n < len && in[n] == v ;

  // ... code
}

L’utilisation des fonctions lemmes nous permet de raisonner par induction à propos de lemmes sans avoir besoin de preuve interactive. De plus, le déclenchement des lemmes devient beaucoup plus prévisible puisque nous le faisons à la main. Cependant, les lemmes nous permettent de travailler sur plusieurs labels :

/*@
  lemma my_lemma{L1, L2}:  P{L1} ==> P{L2} ;
*/

Les fonctions lemmes ne nous fournissent pas de mécanisme équivalent car elles sont simplement des fonctions C normales, qui ne peuvent pas prendre de labels comme entrée. Regardons ce que nous pouvons faire à ce sujet.

Macro lemme

Lorsque nous devons traiter de multiples labels, l’idée est « d’injecter » directement le code de preuve à l’endroit où c’est nécessaire comme nous l’avons fait au début de ce chapitre. En revanche, nous ne voulons pas écrire ce code à la main chaque fois que nous en avons besoin, utilisons donc des macros pour le faire.

Pour le moment, traduisons notre code précédent en une macro au lieu d’une fonction. Comme nous utilisons la macro dans du code fantôme (donc en annotation), nous devons faire attention à utiliser la syntaxe pour les annotations fantôme lorsque nous écrivons l’invariant de notre boucle et les assertions :

#define element_level_sorted_implies_sorted(_arr, _len) \
  /@ assert element_level_sorted(_arr, _len) ; @/       \
  /@ loop invariant 0 <= _i <= _len ;                   \
     loop invariant sorted(_arr, _i) ;                  \
     loop assigns _i ;                                  \
     loop variant _len-_i ; @/                          \
  for(size_t _i = 0 ; _i < _len ; ++_i){                \
    /@ assert 0 < _i ==> _arr[_i-1] <= _arr[_i] ; @/    \
  }                                                     \
  /@ assert sorted(_arr, _len); @/

/*@ requires \valid_read(arr + (0 .. len-1));
    requires element_level_sorted(arr, len) ;
*/
unsigned bsearch_callee(int* arr, size_t len, int value){
  //@ ghost element_level_sorted_implies_sorted(arr, len) ;
  return bsearch(arr, len, value);
}

Au lieu de fournir un pré et une postcondition, nous énonçons ces propriétés en utilisant des assertions avant eth après le code de preuve. Ce code de preuve est simplement le même qu’avant, et est utilisé exactement comme il était utilisé dans le cas de la fonction. Cependant, nous pouvons voir que cela fait une différence importante une fois qu’il a été préprocessé par Frama-C, puisque le bloc de code et les annotations sont directement injectées dans la fonction bsearch_callee.

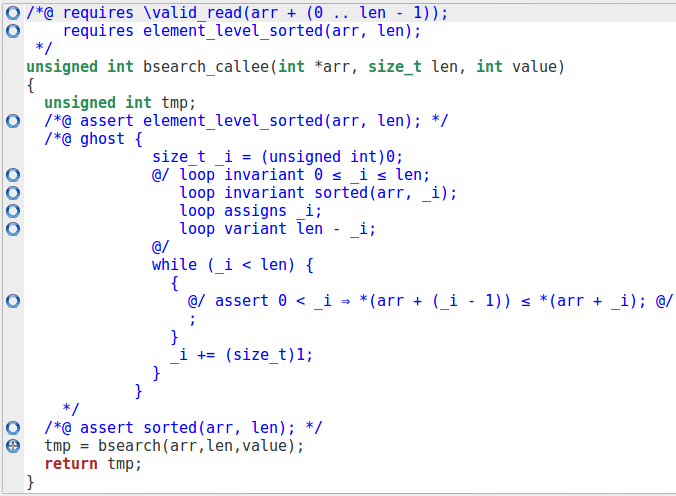
En fait, nous utilisons une macro pour générer le code que nous écrivions précédemment. Dans le cas présent, ce n’est pas vraiment intéressant puisque l’appel de fonction nous permettait d’avoir une preuve plus modulaire. Étudions donc un exemple où nous n’avons pas d’autre choix qu’utiliser une macro.

Nous utiliserons le lemme suivant :

/*@
  predicate shifted{L1, L2}(int* arr, integer fst, integer last, integer shift) =
    \forall integer i ; fst <= i < last ==> \at(arr[i], L1) == \at(arr[i+shift], L2) ;
  lemma shift_ptr{L1, L2}:
    \forall int* arr, integer fst, integer last, integer s1, s2 ;
      shifted{L1, L2}(arr, fst+s1, last+s1, s2) ==> shifted{L1, L2}(arr+s1, fst, last, s2) ;
*/

Avec pour objectif de prouver le programme suivant :

/*@
  requires \valid(array+(beg .. end+shift-1)) ;
  requires shift + end <= UINT_MAX ;
  assigns array[beg+shift .. end+shift-1];
  ensures shifted{Pre, Post}(array, beg, end, shift) ;
*/
void shift_array(int* array, size_t beg, size_t end, size_t shift);

/*@
  requires \valid(array+(0 .. len+s1+s2-1)) ;
  requires s1+s2 + len <= UINT_MAX ;
  assigns array[s1 .. s1+s2+len-1];
  ensures shifted{Pre, Post}(array+s1, 0, len, s2) ;
*/
void callee(int* array, size_t len, size_t s1, size_t s2){
  shift_array(array, s1, s1+len, s2) ;
}

où le lemme shift_ptr est nécessaire pour prouver que la postcondition de callee depuis la postcondition de shift_array. Notre but est bien sûr de ne pas avoir besoin du lemme en le remplaçant par une macro-lemme.

Il n’y a pas de guide précis pour concevoir une macro utilisée pour injecter un code de preuve. Cependant, la plupart des lemmes énoncés à propos de labels multiples sont relativement similaires dans leur manière de lier les labels. Illustrons donc avec cet exemple ; la plupart du temps concevoir une macro dans une telle situation suivra plus ou moins ce schéma.

Pour construire la macro, nous avons besoin d’un contexte dans lequel travailler. Nous construisons ce contexte en utilisant une fonction, nommons-la context_to_prove_shift_ptr. L’idée est d’utiliser cette fonction pour construire notre macro en isolation du reste du programme pour rendre la vérification de la propriété plus facile. Cependant, tandis que les fonctions lemmes sont ensuite appelées dans d’autres fonctions pour déduire des propriétés, cette fonction ne sera jamais appelée, son rôle est juste de nous permettre d’avoir un « endroit » où nous pouvons construire notre preuve. En particulier, comme nous avons besoin de plusieurs labels mémoire, notre fonction a besoin de modifier le contenu de la mémoire (sinon, nous aurions qu’un seul état mémoire pour toute la fonction).

Illustrons cela avec notre problème actuel pour rendre tout cela plus clair. Premièrement, nous créons la macro shift_array qui contiendra notre code de preuve, pour le moment indiquons juste que c’est une instruction vide. Dans les paramètres de ce lemme, nous prenons les labels considérés. Notons que les règles précédemment exprimées à propos des variables quantifiées s’appliquent aussi pour les macros.

#define shift_ptr(_L1, _L2, _arr, _fst, _last, _s1, _s2) ;

Ensuite nous créons notre fonction de contexte :

/*@
  assigns arr[fst+s1+s2 .. last+s1+s2] ;
  ensures shifted{Pre, Post}(arr, fst+s1, last+s1, s2) ;
*/
void assign_array(int* arr, size_t fst, size_t last, size_t s1, size_t s2);

/*@
  requires fst <= last ;
  requires s1+s2+last <= UINT_MAX ;
*/
void context_to_prove_shift_ptr(int* arr, size_t fst, size_t last, size_t s1, size_t s2){
 L1: ;
  assign_array(arr, fst, last, s1, s2);
 L2: ;
  //@ assert shifted{L1, L2}(arr, fst+s1, last+s1, s2) ;

  //@ ghost shift_ptr(L1, L2, arr, fst, last, s1, s2) ;

  //@ assert shifted{L1, L2}(arr+s1, fst, last, s2) ;
}

Décomposons ce code, en commençant par la fonction de contexte. En entrée, nous recevons les variables du lemme. Nous énonçons également quelques propriétés à propos des bornes des entiers considérés, généralement cela devrait simplement être les préconditions qui ne sont pas liées aux états mémoire, ou liées au premier état mémoire. Ensuite, nous introduisons le label L1 et nous appelons la fonction assign_array qui nous amène au label L2. Le rôle de cet appel est de s’assurer que WP créera un nouvel état mémoire (et qu’il ne considérera donc pas que la mémoire est la même), et d’établir les prémisses. En effet, si nous regardons le contrat de assign_array, nous voyons qu’elle assigne le tableau (ce qui garantit la création d’un nouvel état mémoire) et en postcondition, elle assure que le contenu du tableau, entre la pré et la postcondition (donc, quand nous l’appelons : L1 et L2), respecte les prémisses de notre lemme (que l’on répète en ligne 15, en ajoutant une assertion). Ensuite nous utilisons notre macro shift_ptr (qui contiendra par la suite notre code de preuve), et nous voulons être capables de prouver la postcondition de notre lemme (ligne 19).

En faisant cela, nous assurons que nous avons construit un contexte qui ne contient que les informations nécessaires pour construire le code de preuve permettant de déduire la conclusion (ligne 40) depuis les prémisses (ligne 36). Maintenant écrivons la macro.

#define shift_ptr(_L1, _L2, _arr, _fst, _last, _s1, _s2)\
  /@ assert shifted{_L1, _L2}(_arr, _fst+_s1, _last+_s1, _s2) ; @/      \
  /@ loop invariant _fst <= _i <= _last ;                               \
     loop invariant shifted{_L1, _L2}(_arr+_s1, _fst, _i, _s2) ;        \
     loop assigns _i ;                                                  \
     loop variant _last-_i ; @/                                         \
     for(size_t _i = _fst ; _i < _last ; ++_i){                         \
       /@ assert \let _h_i = \at(_i, Here) ;                            \
      \at(_arr[_h_i+_s1], _L1) == \at(_arr[_h_i+_s1+_s2], _L2) ; @/ \
     }                                                                  \
  /@ assert shifted{_L1, _L2}(_arr+_s1, _fst, _last, _s2) ; @/

Nous ne détaillerons pas ce code, car il est très similaire à ce que nous avons écrit au début de cette section. La seule petite subtilité est l’assertion qui permet d’aider les solveurs SMT à relier les positions mémoire entre L1 et L2 aux lignes 8—9. Avec cette macro, nous pouvons voir que l’assertion à la fin de la fonction context_to_prove_shift_ptr est correctement validée. Par conséquent, nous pouvons espérer qu’elle sera capable d’aider les prouveurs à obtenir une conclusion similaire dans un contexte similaire (c’est-à-dire un contexte où nous savons que shifted est validée pour un certain tableau entre labels).

Finalement, nous pouvons compléter la preuve de notre fonction callee en utilisant notre macro lemme :

/*@
  requires \valid(array+(0 .. len+s1+s2-1)) ;
  requires s1+s2 + len <= UINT_MAX ;
  assigns array[s1 .. s1+s2+len-1];
  ensures shifted{Pre, Post}(array+s1, 0, len, s2) ;
*/
void callee(int* array, size_t len, size_t s1, size_t s2){
  shift_array(array, s1, s1+len, s2) ;
  //@ ghost shift_ptr(Pre, Here, array, 0, len, s1, s2) ;
}

Nous pouvons constater que même si cette technique permet d’injecter le code de preuve avec une seule ligne de code, elle peut injecter beaucoup de code à la position où nous l’utilisons. De plus, lorsque nous injectons ce code à un endroit où nous savons qu’il sera utile, le contexte correspondant peut déjà être plutôt complexe. Il n’est donc pas rare d’avoir à modifier légèrement la macro pour ajouter un peu d’information qui n’est pas nécessaire dans un contexte bien propre comme celui que nous utilisons pour produire la macro.

Notons qu’en cela, à la différence de la fonction lemme qui a un comportement très proche d’un lemme « classique », au sens où elle nous permet de faire une déduction immédiate d’une conclusion à partir de certaines prémisses à un point particulier de programme sans avoir à en refaire la preuve ; la macro lemme, elle, s’éloigne beaucoup du comportement d’un lemme « classique », car elle implique de refaire la preuve à chaque point où l’on a besoin de cette déduction.

Tout ceci peut rendre le contexte beaucoup plus gros, et plus difficile à utiliser pour les solveurs SMT. Il y a d’autres limitations à cette technique et le lecteur très attentif aura déjà pu les constater. Parlons-en.

Limitations

La principale limitation des fonctions lemmes et macros lemmes est le fait que nous sommes limités à des types C. Par exemple, si nous comparons notre lemme element_level_sorted_is_sorted avec la fonction lemme correspondante, le type original de la valeur len est un type entier mathématique, tandis que dans la fonction lemme, ce type est size_t. Cela signifie que là où notre lemme était vrai pour tout entier, et donc qu’il pouvait être utilisé peu importe que la variable représentant la taille soit un int, ou un unsigned (ou n’importe quel autre type entier), à l’opposé, notre fonction ne peut être utilisée que pour les types qui peuvent être convertis de manière sûre vers size_t. Cependant, cette limitation n’est généralement pas un problème : nous avons juste à exprimer notre spécification dans le type le plus gros que nous avons à considérer dans notre programme et la plupart du temps cela sera suffisant. Et si ce n’est pas le cas, nous pouvons par exemple dupliquer le lemme pour les types qui nous intéressent. La plupart du temps cette limitation est largement gérable puisque nous travaillons avec les types utilisés dans le programme à prouver.

Dans certains cas, en revanche, cela contraint notre manière de modéliser des propriétés, ce qui est principalement lié aux types logiques que nous pouvons utiliser pour modéliser certaines structures de données concrètes. Par exemple, pour modéliser une liste chaînée, nous pouvons utiliser le type logique ACSL \list<Type> et exprimer une propriété inductive ou axiomatique pour définir comment une liste chaînée concrète peut être modélisée par une liste logique. Nous pourrions donc avoir des lemmes à propos des listes logiques, comme :

/*@
  lemma in_list_in_sublist:
    \forall \list<int> l, l1, l2, int element ;
      l == (l1 ^ l2) ==>      // Here, ^ denotes lists concatenation
      (in_list(element, l) <==> (in_list(element, l1) || in_list(element, l2))) ;
*/

Nous ne pouvons pas écrire une fonction lemme avec du code de preuve pour cette propriété puisque nous n’avons pas de moyen d’utiliser ce type logique dans du code C, et donc, aucun moyen d’écrire une boucle et un invariant qui nous permettraient de prouver cette propriété.

L’autre limitation est liée aux macros lemmes et ce que nous avons déjà mentionné dans le chapitre précédent à propos des assertions. En ajoutant trop d’assertions, le contexte de preuve peut devenir trop gros et trop complexe, et donc difficile à manipuler pour les solveurs SMT. Utiliser des macros lemmes peut générer beaucoup de code et d’annotations et amener à de plus gros contextes preuve. Elles devraient donc être utilisées avec beaucoup de parcimonie.

Finalement, selon la propriété à prouver, il peut être difficile de trouver un code de preuve. En effet, les assistants de preuve comme Coq sont conçus pour être capables d’exprimer des preuves même pour des propriétés très complexes, en se reposant sur une vue très haut niveau de nos problèmes, tandis que C a été conçu pour écrire des programmes, et avec une vue très détaillée de la manière de résoudre le problème. Il peut donc parfois être difficile d’écrire un programme C permettant de prendre en compte certaines propriétés et plus encore de trouver un invariant utilisable lié à nos boucles.

Encore un peu de tri par insertion

Maintenant, revenons à notre preuve du tri par insertion et voyons comment nous pouvons nous débarrasser de nos preuves interactives pour cette fonction. Notons cependant que dans cette preuve, nous avons souvent besoin de macros puisqu’il n’a pas été particulièrement écrit avec comme objectif de le vérifier plus tard (pour cela, le lecteur peut se référer au livre ACSL by Example, qui peut être adapté avec une technique similaire et est beaucoup plus facile à prouver). Donc dans cet exemple, nous poussons les solveurs SMT vers leurs limites à cause des gros contextes de preuve. En fonction de la puissance de la machine sur laquelle la preuve est lancée, la preuve pourrait approcher les 120 secondes (ce qui est déjà long pour un solveur SMT). Dans cet exemple, nous illustrerons les trois cas d’usage que nous avons vu du code fantôme jusqu’ici :

écrire directement un code pour construire une preuve,
écrire (et utiliser) des fonctions lemmes,
écrire (et utiliser) des macros lemmes.

Nous utilisons également des assertions pour rendre le contexte de preuve plus riche afin que les solveurs SMT puissent prouver les propriétés qui nous intéressent. Certaines parties des annotations que nous avons écrites précédemment seront équivalentes à ce que nous avons fait précédemment. Nous rappellerons leur but dans chaque fonction. Ensuite, nous utilisons la même définition axiomatiques pour le comptage d’occurrences. De plus, nous conservons ces définitions de prédicats :

/*@
  predicate sorted(int* a, integer b, integer e) =
    \forall integer i, j; b <= i <= j < e ==> a[i] <= a[j];
  predicate shifted{L1, L2}(integer s, int* a, integer beg, integer end) =
    \forall integer k ; beg <= k < end ==> \at(a[k], L1) == \at(a[s+k], L2) ;
  predicate unchanged{L1, L2}(int* a, integer beg, integer end) =
    shifted{L1, L2}(0, a, beg, end);
  predicate rotate_left{L1, L2}(int* a, integer beg, integer end) =
    beg < end && \at(a[beg], L2) == \at(a[end-1], L1) &&
    shifted{L1, L2}(1, a, beg, end - 1) ;
  predicate permutation{L1, L2}(int* in, integer from, integer to) =
    \forall int v ; l_occurrences_of{L1}(v, in, from, to) ==
                    l_occurrences_of{L2}(v, in, from, to) ;
*/

puisque nous en avons besoin, ainsi que le lemme à propos de la transitivité du comptage d’occurrences, puisqu’il était prouvé automatiquement par les solveurs SMT (nous pouvons donc le garder puisqu’il ne nécessite pas de preuve interactive de notre part).

/*@ lemma transitive_permutation{L1, L2, L3}:
  \forall int* a, integer beg, integer end ;
    permutation{L1, L2}(a, beg, end) ==> 
    permutation{L2, L3}(a, beg, end) ==> 
      permutation{L1, L3}(a, beg, end) ;
*/

Commençons par la fonction insertion_sort. Dans cette fonction, nous avons écrit trois assertions :

/*@
  requires beg < end && \valid(a + (beg .. end-1));
  assigns a[beg .. end-1];
  ensures sorted(a, beg, end);
  ensures permutation{Pre, Post}(a,beg,end);
*/
void insertion_sort(int* a, size_t beg, size_t end){
  /*@
    loop invariant beg+1 <= i <= end ;
    loop invariant sorted(a, beg, i) ;
    loop invariant permutation{Pre, Here}(a,beg,end);
    loop assigns a[beg .. end-1], i ;
    loop variant end-i ;
  */
  for(size_t i = beg+1; i < end; ++i) {
    //@ ghost L: ;
    insert(a, beg, i);
    //@ assert permutation{L, Here}(a, beg, i+1);
    //@ assert unchanged{L, Here}(a, i+1, end) ;
    //@ assert permutation{L, Here}(a, beg, end) ;
  }
}

La première nous assure que le début du tableau où nous avons inséré une valeur est une permutation de la même plage de valeur avant l’appel à insert. Comme c’est la postcondition de la fonction, elle n’est pas nécessaire, mais nous la conservons pour illustration. La dernière assertion est la propriété que nous voulons prouver pour obtenir suffisamment de connaissance pour que le lemme à propos de la transitivité de la permutation soit utilisé (et montre qu’à la fin du bloc de la boucle, puisque le tableau est une permutation du tableau au début, qui est lui-même une permutation du tableau original, alors le tableau à la fin du corps est une permutation du tableau original).

La seconde assertion dit que la seconde partie du tableau reste inchangée, et nous voulons utiliser cette connaissance pour montrer que le nombre d’occurrences des valeurs n’a pas changé. Ici, nous pourrions utiliser une combinaison des fonctions et macros lemmes pour prouver que la plage complète est une permutation (comme nous le ferons pour l’autre fonction). Cependant ici, écrire directement le code est un peu plus simple et requiert moins de preuves (comme nous le verrons plus tard), écrivons donc directement le code qui permet de prouver notre propriété.

Pour montrer que la plage complète est une permutation, nous devons montrer que le nombre d’occurrences de chaque valeur n’a pas changé. Nous savons que la première partie du tableau est une permutation de la même plage au début du corps de la boucle. Donc, nous savons déjà que le nombre d’occurrences de chaque $v$ n’a pas changé pour une partie de notre tableau. En utilisant une boucle avec j allant de i à end et un invariant permutation{L,PI}(a, beg, j), nous pouvons continuer le comptage des occurrences pour le reste de notre tableau, avec la connaissance que la fin n’a pas changé (quand i+1 est plus petit que end sinon nous n’avons simplement plus rien à compter):

  for(size_t i = beg+1; i < end; ++i) {
    //@ ghost L: ;
    insert(a, beg, i);
    //@ ghost PI: ;
    //@ assert permutation{L, PI}(a, beg, i+1);
    //@ assert unchanged{L, PI}(a, i+1, end) ;
    /*@ ghost
      if(i+1 < end){
        /@ loop invariant i+1 <= j <= end ;
           loop invariant permutation{L, PI}(a, beg, j) ;
           loop assigns j ;
           loop variant end - j ;
        @/
        for(size_t j = i+1 ; j < end ; ++j);
      }
    */
  }

ce qui est suffisant pour assurer que la fonction insertion_sort respecte sa spécification à condition de finir la preuve de la fonction insert. Cette seconde fonction réalise des actions plus complexes, nous partirons de cette version annotée :

/*@
  requires beg < last < UINT_MAX && \valid(a + (beg .. last));
  requires sorted(a, beg, last) ;
  assigns a[ beg .. last ] ;
  
  ensures permutation{Pre, Post}(a, beg, last+1);
  ensures sorted(a, beg, last+1) ;
*/
void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;

  /*@
    loop invariant beg <= i <= last ;
    loop invariant \forall integer k ; i <= k < last ==> a[k] > value ;
    loop invariant \forall integer k ; beg <= k <= i    ==> a[k] == \at(a[k], Pre) ;
    loop invariant \forall integer k ; i+1 <= k <= last ==> a[k] == \at(a[k-1], Pre) ;
    loop assigns i, a[beg .. last] ;
    loop variant i ;
  */
  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }
  a[i] = value ;
  //@ assert sorted(a, beg, last+1) ;

  //@ assert rotate_left{Pre, Here}(a, i, last+1) ;
  //@ assert permutation{Pre, Here}(a, i, last+1) ;

  //@ assert unchanged{Pre, Here}(a, beg, i) ;
  //@ assert permutation{Pre, Here}(a, beg, i) ;
}

À nouveau, la preuve que cette fonction maintient la permutation du tableau est la partie la plus difficile de notre travail. Le fait que cette fonction garantisse que les valeurs sont bien triées est déjà établie. Utiliser la même technique que pour la fonction insertion_sort n’est pas si simple ici. En effet, la seconde partie du tableau a été « tournée » ce qui rend la propriété un peu plus complexe. Du coup, commençons par séparer notre tableau à la position d’insertion en deux parties, où nous montrons respectivement que :

pour la première partie, puisqu’elle est inchangée, pour tout $v$ le nombre d’occurrences n’a pas changé non plus ;
pour la seconde partie, puisqu’elle a tourné, pour tout $v$ , le nombre d’occurrences n’a pas changé.

D’abord, définissons une fonction lemme qui permet d’explicitement couper une plage de valeur en deux sous-parties dans lesquelles nous pouvons compter séparément :

/*@ ghost
  /@ 
    requires beg <= split <= end ;
  
    assigns \nothing ;
  
    ensures \forall int v ;
      l_occurrences_of(v, a, beg, end) ==
      l_occurrences_of(v, a, beg, split) + l_occurrences_of(v, a, split, end) ;
  @/
  void l_occurrences_of_explicit_split(int* a, size_t beg, size_t split, size_t end){
    /@
      loop invariant split <= i <= end ;
      loop invariant \forall int v ; l_occurrences_of(v, a, beg, i) ==
        l_occurrences_of(v, a, beg, split) + l_occurrences_of(v, a, split, i) ;
      loop assigns i ;
      loop variant end - i ;
    @/    
    for(size_t i = split ; i < end ; ++i);
  }
*/

Nous pouvons noter que cette propriété est prouvée d’une manière qui est très similaire à ce que nous avons écrit dans le corps de la boucle de la fonction insertion_sort, nous commençons au point à partir duquel nous voulons compter et nous montrons que la propriété reste vraie pour le reste du tableau.

Nous pouvons utiliser notre fonction pour couper le tableau à la bonne position après la boucle. Cependant, nous ne pouvons le faire que pour le nouveau contenu du tableau. En effet, pour établir cela pour le tableau original, nous devons appeler la fonction sur le tableau original pour lequel nous ne connaissons pas encore la valeur de $i$ . Par conséquent, écrivons une autre version de la propriété « split » qui nous montrer que nous pouvons couper le tableau à toute position, donc rendons la variable split universellement quantifiée, et utilisons la fonction précédente pour montrer que cette nouvelle propriété est vraie.

/*@ ghost
  /@ 
    requires beg <= end ;
    assigns \nothing ;
    ensures \forall int v, size_t split ; beg <= split <= end ==>
      l_occurrences_of(v, a, beg, end) ==
      l_occurrences_of(v, a, beg, split) + l_occurrences_of(v, a, split, end) ;
  @/
  void l_occurrences_of_split(int* a, size_t beg, size_t end){
    /@
      loop invariant beg <= i <= end ;
      loop invariant \forall int v, size_t split ; beg <= split < i ==>
        l_occurrences_of(v, a, beg, end) ==
        l_occurrences_of(v, a, beg, split) + l_occurrences_of(v, a, split, end) ;
      loop assigns i ;
      loop variant end - i ;
    @/
    for(size_t i = beg ; i < end ; ++i){
      l_occurrences_of_explicit_split(a, beg, i, end);
    }
  }
*/

Et nous pouvons couper notre tableau original et le nouveau :

void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;
  // split before modifying
  //@ ghost l_occurrences_of_split(a, beg, last+1);

  /*@ LOOP ANNOT */
  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }
  a[i] = value ;
  // Assertions ...

  // split after modifying, now we know "i"
  //@ ghost l_occurrences_of_explicit_split(a, beg, i, last+1);
}

Maintenant, les seules parties restantes de la preuve sont de montrer qu’un tableau inchangé est une permutation et ensuite que la rotation maintient également une permutation. Ici, nous avons besoin d’une macro. Commençons avec la plus facile : le tableau inchangé, que l’on a prouvé quasiment à l’identique dans la fonction insertion_sort. Nous commençons par construire notre contexte de preuve :

/*@
  assigns arr[fst .. last-1] ;
  ensures unchanged{Pre, Post}(arr, fst, last);
*/
void unchanged_permutation_premise(int* arr, size_t fst, size_t last);

/*@
  requires fst <= last ;
*/
void context_to_prove_unchanged_permutation(int* arr, size_t fst, size_t last){
 L1: ;
  unchanged_permutation_premise(arr, fst, last);
 L2: ;
  //@ ghost unchanged_permutation(L1, L2, arr, fst, last) ;

  //@ assert permutation{L1, L2}(arr, fst, last) ;
}

La fonction unchanged_permutation_premise assure que nous avons modifié le tableau (et donc créé un nouvel état mémoire) et que le tableau est inchangé entre la précondition et la postcondition. Nous pouvons construire notre macro lemme :

#define unchanged_permutation(_L1, _L2, _arr, _fst, _last)      \
  /@ assert unchanged{_L1, _L2}(_arr, _fst, _last) ; @/         \
  /@ loop invariant _fst <= _i <= _last ;                       \
     loop invariant permutation{_L1, _L2}(_arr, _fst, _i) ;     \
     loop assigns _i ;                                          \
     loop variant _last - _i ;                                  \
   @/                                                           \
   for(size_t _i = _fst ; _i < _last ; ++_i) ;                  \
   /@ assert permutation{_L1, _L2}(_arr, _fst, _last); @/

qui correspond presque à ce que nous avons écrit pour insert_sort, et utiliser cette macro là où nous en avons besoin dans la fonction insert.

//@ assert unchanged{Pre, Here}(a, beg, i) ;
//@ ghost unchanged_permutation(Pre, Here, a, beg, i) ;
//@ assert permutation{Pre, Here}(a, beg, i) ;

La seule propriété restante est la plus complexe et concerne le prédicat rotate_left. Écrivons d’abord un contexte pour préparer notre macro.

/*@
  assigns arr[fst .. last-1] ;
  ensures rotate_left{Pre, Post}(arr, fst, last);
*/
void rotate_left_permutation_premise(int* arr, size_t fst, size_t last);

/*@
  requires fst < last ;
*/
void context_to_prove_rotate_left_permutation(int* arr, size_t fst, size_t last){
 L1: ;
  //@ ghost l_occurrences_of_explicit_split(arr, fst, last-1, last) ;
  rotate_left_permutation_premise(arr, fst, last);
 L2: ;
  //@ ghost rotate_left_permutation(L1, L2, arr, fst, last) ;

  //@ assert permutation{L1, L2}(arr, fst, last) ;
}

Comment pouvons-nous prouver cette propriété ? Nous devons d’abord constater que puisque tous les éléments depuis le début jusqu’à l’avant-dernier ont été décalés d’une cellule, le nombre d’occurrences dans cette partie décalée n’a pas changé. Ensuite, nous devons montrer que le nombre d’occurrences de $v$ respectivement dans la dernière cellule du tableau original et la première cellule du nouveau tableau est le même (puisque l’élément correspondant est le même). À nouveau, nous nous reposons sur la fonction split pour compter séparément les éléments décalés et l’élément qui est déplacé de la fin vers le début. Cependant, l’appel correspondant dans le tableau original doit à nouveau être réalisée avant le code qui modifie le tableau original (voir ligne 194) dans le code précédent, et nous devons prendre cela en compte quand nous insérerons notre utilisation de la macro dans la fonction insert.

Présentons maintenant la macro qui est utilisée pour prouver que notre lemme est valide :

#define rotate_left_permutation(_L1, _L2, _arr, _fst, _last)            \
  /@ assert rotate_left{_L1, _L2}(_arr, _fst, _last) ; @/               \
  /@ loop invariant _fst+1 <= _i <= _last ;                             \
     loop invariant \forall int _v ;                                    \
       l_occurrences_of{_L1}(_v, _arr, _fst, \at(_i-1, Here)) ==        \
       l_occurrences_of{_L2}(_v, _arr, _fst+1, \at(_i, Here)) ;         \
     loop assigns _i ;                                                  \
     loop variant _last - _i ;                                          \
   @/                                                                   \
   for(size_t _i = _fst+1 ; _i < _last ; ++_i) {                        \
     /@ assert \at(_arr[\at(_i-1, Here)], _L1) ==                       \
               \at(_arr[\at(_i, Here)], _L2) ;                          \
     @/                                                                 \
   }                                                                    \
   l_occurrences_of_explicit_split(_arr, _fst, _fst+1, _last) ;         \
   /@ assert \forall int _v ;                                           \
     l_occurrences_of{_L1}(_v, _arr, _fst, _last) ==                    \
       l_occurrences_of{_L1}(_v, _arr, _fst, _last-1) +                 \
       l_occurrences_of{_L1}(_v, _arr, _last-1, _last) ;                \
   @/                                                                   \
   /@ assert \at(_arr[_fst], _L2) == \at(_arr[_last-1], _L1) ==>        \
     (\forall int _v ;                                                  \
       l_occurrences_of{_L2}(_v, _arr, _fst, _fst+1) ==                 \
       l_occurrences_of{_L1}(_v, _arr, _last-1, _last)) ;               \
   @/                                                                   \
   /@ assert permutation{_L1, _L2}(_arr, _fst, _last); @/

L’invariant de boucle est très similaire à ce que nous avons écrit jusqu’à maintenant, la seule différence est que nous devons tenir compte du glissement des éléments. De plus, pour l’invariant, nous avons dû ajouter une assertion pour aider les prouveurs automatiques à remarquer que le dernier élément de chaque plage est le même (notons que selon les versions des prouveurs ou la puissance de la machine, cela peut parfois ne pas être nécessaire). Une différence plus importante comparativement à nos exemples précédents est le fait qu’ici, nous devons fournir plus d’information aux SMT solveurs en ajoutant d’autres appels de fonction fantôme (ligne 14, pour couper le premier élément du tableau), ainsi que des assertions pour guider les dernières étapes de preuve :

15—19 : nous rappelons que le tableau original peut être coupé au niveau du dernier élément,
20—23 : nous montrons que comme le premier élément du tableau est le dernier élément du tableau original (20), le nombre d’occurrences pour toute valeur dans ces plages est le même (21—23).

Nous pouvons utiliser cette macro dans notre programme :

//@ assert rotate_left{Pre, Here}(a, i, last+1) ;
//@ ghost rotate_left_permutation(Pre, Here, a, i, last+1) ;
//@ assert permutation{Pre, Here}(a, i, last+1) ;

Cependant, nous avons besoin de montrer que la plage au label Pre peut être coupée à last. Pour cela, nous utilisons une autre variante de la fonction split, qui montre que toute sous-plage peut être coupée avant le dernier élément (si elle n’est pas vide) :

/*@ ghost
  /@
    requires beg < end ;
    assigns \nothing ;
    ensures \forall int v, size_t any ; beg <= any < end ==>
      l_occurrences_of(v, a, any, end) ==
      l_occurrences_of(v, a, any, end-1) + l_occurrences_of(v, a, end-1, end) ;
  @/
  void l_occurrences_of_from_any_split_last(int* a, size_t beg, size_t end){
    /@
      loop invariant beg <= i <= end-1 ;
      loop invariant \forall int v, size_t j ;
        beg <= j < i ==>
        l_occurrences_of(v, a, j, end) ==
        l_occurrences_of(v, a, j, end-1) + l_occurrences_of(v, a, end-1, end) ;
      loop assigns i ;
      loop variant (end - 1) - i ;
    @/
    for(size_t i = beg ; i < end-1 ; ++i){
      l_occurrences_of_explicit_split(a, i, end-1, end);
    }
  }
*/

que nous pouvons ensuite appeler avant la boucle de la fonction insert :

void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;

  //@ ghost l_occurrences_of_split(a, beg, last+1);
  //@ ghost l_occurrences_of_from_any_split_last(a, beg, last+1);

Notons que selon les versions des prouveurs automatiques, les assertions en lignes 16 à 18 de la macro, à propos de l’élément au début et à la fin du tableau, pourraient ne pas être prouvées à cause de la complexité du contexte de preuve. Aidons les solveurs une dernière fois en ajoutant un dernier lemme, automatiquement prouvé par les solveurs SMT, qui nous énonce la relation en question pour tout tableau et toute position du tableau :

/*@ lemma one_same_element_same_count{L1, L2}:
  \forall int* a, int* b, int v, integer pos_a, pos_b ;
    \at(a[pos_a], L1) == \at(b[pos_b], L2) ==>
    l_occurrences_of{L1}(v, a, pos_a, pos_a+1) == 
    l_occurrences_of{L2}(v, b, pos_b, pos_b+1) ;
*/

qui nous garantit que la fonction annotée résultante est entièrement prouvée :

/*@
  requires beg < last < UINT_MAX && \valid(a + (beg .. last));
  requires sorted(a, beg, last) ;
  assigns a[ beg .. last ] ;
  
  ensures permutation{Pre, Post}(a, beg, last+1);
  ensures sorted(a, beg, last+1) ;
*/
void insert(int* a, size_t beg, size_t last){
  size_t i = last ;
  int value = a[i] ;

  //@ ghost l_occurrences_of_split(a, beg, last+1);
  //@ ghost l_occurrences_of_from_any_split_last(a, beg, last+1);

  /*@
    loop invariant beg <= i <= last ;
    loop invariant \forall integer k ; i <= k < last ==> a[k] > value ;
    loop invariant \forall integer k ; beg <= k <= i    ==> a[k] == \at(a[k], Pre) ;
    loop invariant \forall integer k ; i+1 <= k <= last ==> a[k] == \at(a[k-1], Pre) ;
    loop assigns i, a[beg .. last] ;
    loop variant i ;
  */
  while(i > beg && a[i - 1] > value){
    a[i] = a[i - 1] ;
    --i ;
  }
  a[i] = value ;
  //@ assert sorted(a, beg, last+1) ;

  /*@ assert
      \forall int v ;
      l_occurrences_of{Pre}(v, a, \at(i, Here), last+1) ==
        l_occurrences_of{Pre}(v, a, \at(i, Here), last) +
    l_occurrences_of{Pre}(v, a, last, last +1);
  */

  //@ assert rotate_left{Pre, Here}(a, i, last+1) ;
  //@ ghost rotate_left_permutation(Pre, Here, a, i, last+1) ;
  //@ assert permutation{Pre, Here}(a, i, last+1) ;

  //@ assert unchanged{Pre, Here}(a, beg, i) ;
  //@ ghost unchanged_permutation(Pre, Here, a, beg, i) ;
  //@ assert permutation{Pre, Here}(a, beg, i) ;

  //@ ghost l_occurrences_of_explicit_split(a, beg, i, last+1);
}

Nous mettons finalement en valeur le fait que le contexte de preuve peut rendre le travail vraiment difficile pour les solveurs SMT. Tout simplement, si nous inversons les preuves à propos du chaque partie du tableau, à savoir, en commençant par la partie unchanged puis la partie rotate, la preuve a de très bonnes chances d’échouer, car elle fait grossir le contexte de preuve pour la preuve la plus difficile. Pour la même raison, il est ici presque obligatoire (mais cela dépend quand même de la puissance des solveurs et de la machine) de séparer les preuves d’absence d’erreur à l’exécution, sinon elles polluent le contexte de preuve et cela peut entraîner l’échec de la preuve.

Exercices

La somme des N premiers entiers

En utilisant des fonctions lemmes, nous pouvons prouver le lemme à propos de la somme des N premiers entiers. Vous avez peut-être déjà fait cette preuve au lycée ; maintenant, il est temps de faire cette preuve en C et ACSL. Écrire un contrat pour la fonction suivante qui exprimer en postcondition que la somme des N premiers entiers est N(N+1)/2. Compléter le corps de la fonction avec une boucle pour prouver la propriété. Nous conseillons de légèrement modifier l’invariant pour faire disparaître la division (qui sur les entiers a certaines propriétés qui rendent son utilisation difficile avec des solveurs SMT en fonction des contraintes qui existent sur les valeurs utilisées).

/*@
  logic integer sum_of_n_integers(integer n) =
    (n <= 0) ? 0 : sum_of_n_integers(n-1) + n ;
*/

/*@ ghost
  /@
    assigns \nothing ;
    ensures ... ;
  @/
  void lemma_value_of_sum_of_n_integers_2(unsigned n){
    // ...
  }
*/

Maintenant, généralisons à toutes bornes avec la somme de tous les entiers entre deux bornes fst et lst. Nous fournissons la fonction logique et le contrat, à vous d’écrire le corps de la fonction de manière à vérifier la postcondition. À nouveau, nous conseillons d’exprimer l’invariant sans division.

/*@
  logic integer sum_of_range_of_integers(integer fst, integer lst) =
    ((lst <= fst) ? lst : lst + sum_of_range_of_integers(fst, lst-1)) ;
*/

/*@ ghost
  /@
    requires fst <= lst ;
    assigns \nothing ;
    ensures ((lst-fst+1)*(fst+lst))/2 == sum_of_range_of_integers(fst, lst) ;
  @/
  void lemma_value_of_sum_of_range_of_integers(int fst, int lst){
    // ...
  }
*/

Finalement, prouver cette fonction :

/*@
  requires n*(n+1) <= UINT_MAX ;
  assigns \nothing ;
  ensures \result == sum_of_n_integers(n);
*/
unsigned sum_n(unsigned n){
  return (n*(n+1))/2 ;
}

Cela ne devrait pas être trop difficile, et ce que nous obtenons est une preuve que nous avons écrit une optimisation correcte pour la fonction qui calcule la somme des N premiers entiers.

Propriétés à propos du comptage d’occurrence

Dans cet exercice, nous voulons prouver un ensemble de propriétés intéressantes à propos de notre définition logique l_occurrences_of :

#include <stddef.h>

/*@ ghost
  void occ_bounds(int v, int* arr, size_t len){
    // ...
  }

  void not_in_occ_0(int v, int* arr, size_t len){
    // ...
  }

  void occ_monotonic(int v, int* arr, size_t pos, size_t more){
    // ...
  }

  void occ_0_not_in(int v, int* arr, size_t len){
    // ...
    // needs occ_monotonic
  }

  size_t occ_pos_find(int v, int* arr, size_t len){
    // ...
    // needs occ_monotonic
  }

  void occ_pos_exists(int v, int* arr, size_t len){
    // ...
    // should use occ_pos_find
  }
*/

La fonction occ_bounds doit énoncer que le nombre d’occurrences de v dans un tableau est compris entre 0 et len.

La fonction not_in_occ_0 doit énoncer que si v n’est pas dans le tableau alors le nombre d’occurrences de v est 0.

La fonction occ_monotonic doit énoncer que le nombre d’occurrences de v dans un tableau entre 0 et pos est inférieur ou égal au nombre d’occurrences de v entre 0 et more si more est supérieur ou égal à pos.

La fonction occ_0_not_in doit énoncer que si le nombre d’occurrences de v dans le tableau est 0 alors v n’est pas dans le tableau. Notons que occ_monotonic serait probablement utile.

La fonction occ_pos_find doit trouver un indice i tel que arr[i] est v, à supposer que le nombre d’occurrences de v est positif. occ_monotonic peut être utile.

Finalement, la fonction occ_pos_exists doit traduire le contrat de la fonction précédente en utilisant une variable quantifiée existentitellement, et utiliser la fonction précédente pour obtenir gratuitement la preuve.

Pour toutes ces fonctions, WP doit être paramétré avec le contrôle d’absence d’erreurs d’exécution ainsi que les options -warn-unsigned-overflow et -warn-unsigned-downcast.

Un exemple avec la somme

Reprendre la preuve effectuée dans le chapitre précédent pour l’exercice à propos de la somme dans un tableau. Modifier les annotations pour assurer que plus aucun lemme classique n’est nécessaire. Voici un squelette pour le fichier :

#include <limits.h>
#include <stddef.h>

/*@
  axiomatic Sum_array{
    logic integer sum(int* array, integer begin, integer end) reads array[begin .. (end-1)];
   
    axiom empty: 
      \forall int* a, integer b, e; b >= e ==> sum(a,b,e) == 0;
    axiom range:
      \forall int* a, integer b, e; b < e ==> sum(a,b,e) == sum(a,b,e-1)+a[e-1];
  }
*/

/*@
  predicate unchanged{L1, L2}(int* array, integer begin, integer end) =
    \forall integer i ; begin <= i < end ==> \at(array[i], L1) == \at(array[i], L2) ;
*/

/*@ ghost
  void sum_separable(int* array, size_t begin, size_t split, size_t end){
    // ...
  }
*/

#define unchanged_sum(_L1, _L2, _arr, _beg, _end) ;


/*@
  requires i < len ;
  requires array[i] < INT_MAX ;
  requires \valid(array + (0 .. len-1));
  assigns array[i];
  ensures sum(array, 0, len) == sum{Pre}(array, 0, len)+1;
*/
void inc_cell(int* array, size_t len, size_t i){
  // ...
  array[i]++ ;
  // ...
}

À mesure que nous essayons de prouver des propriétés plus complexes, particulièrement quand les programmes contiennent des boucles et des structures de données complexes, il y a une part de « trial and error » pour comprendre ce qui manque aux prouveurs pour établir la preuve.

Il peut manquer des hypothèses. Dans ce cas, nous pouvons essayer d’ajouter des assertions pour guider les prouveurs, ou écrire du code ghost avec les bons invariants, ce qui permet d’effectuer une part du raisonnement nous même lorsque c’est trop difficile pour les solveurs SMT.

Avec un peu d’expérience, il est possible de lire le contenu des obligations de preuve ou essayer de faire la preuve soi-même avec l’assistant de preuve Coq pour voir si la preuve semble réalisable. Parfois, le prouveur a juste besoin de plus de temps, dans ce cas, nous pouvons augmenter (parfois beaucoup) le temps de timeout. Bien sûr la propriété peut parfois être trop difficile pour le prouveur et le code ghost ne pas être adapté, dans ce cas, il sera nécessaire de terminer la preuve nous-mêmes.

Finalement, l’implémentation peut être incorrecte, et dans ce cas, nous devons la corriger. À ce moment-là, nous utiliserons du test et non de la preuve, car un test nous permettra de mettre en évidence la présence du bug et de l’analyser.

Principe

Exemple: la fonction recherche

Avantages et limitations

Exercices

Exemple simple

Inverse

Recherche dichotomique

Tri

Contexte de preuve

Déclencher les lemmes

Un exemple plus complexe : du tri à nouveau

Comment utiliser correctement les assertions ?

Exercices

Comprendre le contexte de preuve

Déclencher les lemmes

Déclencher les lemmes sous condition

Un exemple avec la somme

Preuve par induction

Fonction lemme

Macro lemme

Limitations

Encore un peu de tri par insertion

Exercices

La somme des N premiers entiers

Propriétés à propos du comptage d’occurrence

Un exemple avec la somme

Un exemple plus complexe : du tri à nouveau

Comment utiliser correctement les assertions ?