Tracer et dessiner

Pour pouvoir se repérer dans la fenêtre, turtle met en place un repère à deux dimensions. Par défaut, celui-ci est centré dans la fenêtre. Ce repère nous permet de nous déplacer aisément de x sur l’axe des abscisses et de y sur l’axe des ordonnées. Le centre du repère, c’est-à-dire le point (x = 0, y = 0), est l’endroit où le curseur apparaît, sa maison en quelque sorte. Cela n’est pas bien compliqué à comprendre, il faut juste s’habituer à penser dans le plan. L’image suivante permet de mieux visualiser ce que nous venons de dire et comporte quelques exemples de points :

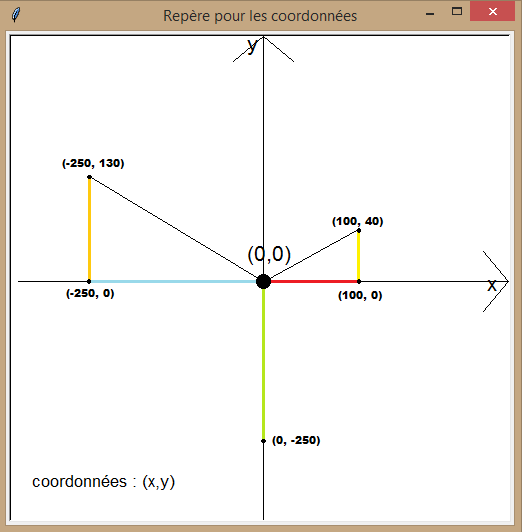
Nettoyer l’écran

Au cours de notre utilisation de turtle, il est possible que nous ayons besoin de nettoyer l’écran. Pour cela, nous pouvons utiliser clear qui permet d’effacer ce que nous avons dessiné. En plus, nous pouvons aussi utiliser reset qui fait la même chose et réinitialise les valeurs du curseur à leurs valeurs par défaut (le crayon retourne à l’origine du repère, retrouve son orientation originale, sa largeur de trait par défaut, etc…). Ces deux fonctions ne modifient donc pas les configurations liées à la fenêtre, comme le titre ou la couleur de fond par exemple. Enfin, elles ne prennent aucun paramètre.

turtle.clear()  #Efface les dessins du crayon
turtle.reset()  #Fait de même et réinitialise le crayon

Avancer et reculer

Pour tracer, il faut se déplacer. Et pour déplacer le curseur, turtle nous offre plusieurs fonctions, comme forward et backward, respectivement pour avancer et reculer d’une distance que l’on passe en paramètre. Elles ont aussi chacune leur version abrégée, respectivement fdet bk.

turtle.forward(turtle.window_width()/3)  #Avance d'un tiers de la largeur de la fenêtre
turtle.backward(turtle.window_width()/2)  #Recule de la moitié de la largeur de la fenêtre
turtle.bk(50)  #Recule de 50px
turtle.fd(0)  #Avance de 0px, donc n'avance pas

Se déplacer à des coordonnées données

Avec goto, en lui fournissant une coordonnée x et une coordonnée y, nous pouvons nous rendre directement à un point (x, y) donné. De plus, nous pouvons aussi modifier uniquement la position en abscisse du curseur avec setx et la position en ordonnée avec sety, en leur passant la nouvelle valeur. Enfin, puisque nous avons parlé du centre du repère, notons que la fonction home permet d’y retourner.

turtle.goto(100, 100)  #Position (100, 100)
turtle.setx(20)  #Position(20, 100)
turtle.sety(-80)  #Position(20, -80)
turtle.home()  #Position(0, 0) (équivalent à turtle.goto(0, 0))

Lever ou baisser le crayon

Si nous ne pouvions pas nous déplacer dans la fenêtre sans laisser de trace, ce ne serait pas très amusant. Or, la fonction up nous permet de lever le crayon tandis que la fonction down nous permet de l’abaisser. Elles ne prennent aucun paramètre. Grâce à elles, nous pouvons choisir de tracer ou non :

turtle.up()  #Lève le crayon
turtle.forward(150)  #Avance de 150px sans tracer
turtle.down()  #Abaisse le crayon
turtle.backward(50)  #Recule de 50px en traçant

Changer la taille du traçage

Faire des traits, c’est bien, mais pouvoir choisir la taille, c’est encore mieux. En passant la nouvelle largeur de nos traits à pensize, nous pouvons le faire. En ne passant rien, la fonction nous renvoie la taille actuelle.

print(turtle.pensize())  #Affiche '1'
turtle.pensize(5.5)  #Modifie la largeur du traçage
print(turtle.pensize())  #Affiche '5.5'

Pour le moment, ce sont des fonctions plutôt basiques. Ce serait plus intéressant de pouvoir faire des figures, en assemblant les traits, et c’est ce que nous allons faire dans la section suivante !

Jusqu’à présent, nous avons vu comment ouvrir une fenêtre et comment nous déplacer dans celle-ci. À présent, nous allons aller encore plus loin en dessinant nos premières figures.

Changer l’angle

Pour dessiner aisément, il nous manque tout de même quelque chose, et je pense que vous vous en êtes rendu compte : il faut que l’on puisse choisir l’inclinaison de notre trait, c’est-à-dire l’angle. En effet, jusqu’à présent nous avons été limités dans nos déplacements.

Or, turtle nous permet justement de faire varier la direction du curseur. Par défaut, lorsque l’on ouvre une fenêtre avec turtle, le crayon est orienté vers l’Est : l’angle est de 0 (ou 360). Pour jouer avec les angles, nous avons les fonctions right et left qui permettent de tourner respectivement vers la droite ou vers la gauche d’un angle passé. Parfois, il est plus simple d’utiliser setheading qui change directement l’angle avec la valeur passée. Vous pouvez aussi connaître la direction actuelle de votre crayon en utilisant la fonction heading qui ne prend aucun paramètre. Toutes ces explications sont illustrées avec l’image ci-dessous ainsi que par l’exemple qui la suit :

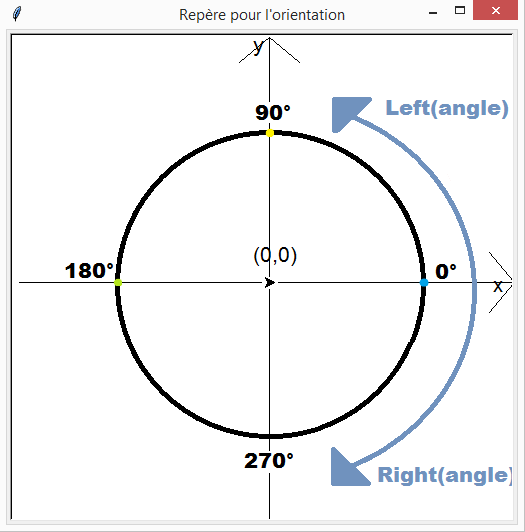
turtle.setup()  #Initialise la fenêtre 
print(turtle.heading())  #Affiche 0.0 : le crayon pointe vers le point bleu : Est
turtle.left(90)  #Pointe vers le point jaune : Nord
turtle.right(270)  #Pointe vers le point vert : Ouest
turtle.setheading(0)  #Pointe de nouveau vers le point bleu
turtle.setheading(-90)  #Pointe à l'opposé du point jaune : Sud
print(turtle.heading())  #Affiche '270.0'

Concrètement, vous conviendrez que nous sommes désormais beaucoup plus libres. N’hésitez pas à essayer et à vous approprier ces notions, car elles seront vraiment utiles pour la suite. Voici un exemple d’utilisation de ce que l’on vient d’apprendre :

Code :

import turtle

LARGEUR, HAUTEUR = 640, 480

if __name__ == "__main__":
    turtle.forward(LARGEUR/3)  #Avance de d'un tiers de la largeur
    turtle.left(80)  #Tourne de 80° à gauche
    turtle.up()  #Lève le curseur
    turtle.forward(HAUTEUR/4)  #Avance d'un quart de la hauteur
    turtle.down()  #Baisse le curseur
    turtle.right(180)  #Tourne à 180 à droite
    turtle.backward(HAUTEUR/4)  #Recule d'un quart de la hauteur
    turtle.pensize(3)  #Change l'épaisseur du tracé
    turtle.home()  #Retourne à la maison
    turtle.exitonclick()  #Clique gauche pour fermer 

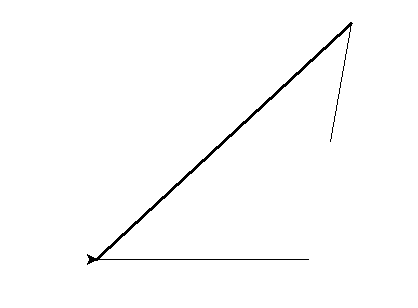
Notons au passage que home réinitialise aussi l’orientation en plus de la position, c’est pourquoi nous voyons que le curseur a un angle de 0 à la fin puisque nous terminons le traitement par cela.

Pour terminer sur les angles, nous pouvons brièvement parler de la fonction towards qui prend en paramètre les coordonnées d’un point et nous retourne l’angle qu’il faudrait pour aller à ce point. Ainsi, ces deux morceaux de code donnent quasiment le même résultat (dans le second cas, l’angle final est celui d’avant l’appel à la fonction)

angle = turtle.towards(0, 90)
print(angle)  #Affiche '90.0'
turtle.setheading(angle)  #Angle : 90.0
turtle.forward(90)  #Position : (0, 90); Angle : 90.0

turtle.goto(0, 90)  #Position : (0, 90); Angle : 0.0

Dessiner des figures simples

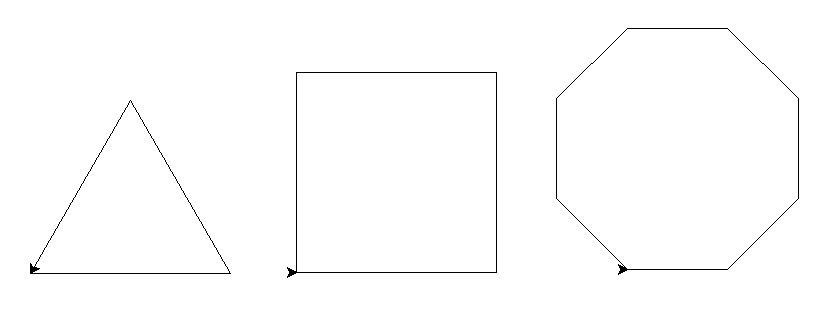
Voilà, nous sommes désormais totalement capable de tracer nos propres figures grâce à ce que nous avons appris. Nous allons donc nous exercer en faisant quelques polygones. Triangle équilatérale, carré et octogone régulier seront nos invités. Avant que vous lisiez la suite, je vous encourage à essayer de dessiner par vous-mêmes ces figures.

Commençons avec le triangle équilatéral. Pour rappel, un triangle équilatéral est un triangle dont les côtés ont la même longueur ce qui implique que chaque angle a une valeur de 60° (par définition, la somme des angles d’un triangle vaut 180°). Une fois que l’on a cela en tête, nous pouvons implémenter une solution explicite :

#Un exemple de triangle équilatéral
longueur_cote = 200
turtle.forward(longueur_cote)  #1er côté
turtle.left(360/3)  #Angle
turtle.forward(longueur_cote)  #2ème côté
turtle.left(360/3)  #Angle
turtle.forward(longueur_cote)  #3ème côté

Pour le carré et l’octogone, nous appliquerons le même principe. Pour le carré, nous avons quatre côtés de même longueur ainsi que quatre angle de 90°. Voici une solution :

#Un exemple de carré
longueur_cote = 200
for i in range(4):
    turtle.forward(longueur_cote)  #Côté
    turtle.left(90)  #Angle

L’octogone a quant à lui 8 côtés et des angles de 45° (360° divisé par 8 côtés). Une solution est :

#Un exemple d'octogone
longueur_cote = 100
for i in range(8):
    turtle.forward(longueur_cote)  #Côté
    turtle.left(360/8)  #Angle

Voilà, pour pratiquer, vous pouvez essayer de dessiner des figures plus compliquées voire de généraliser au cas d’un polygone, ou encore de dessiner à d’autres endroits que depuis le centre du repère. Il est temps de parler d’une dernière figure dont nous n’avons pas encore parlée : le cercle.

Utiliser les cercles

Pour les cercles, nous pouvons éviter de réinventer la roue puisqu’il existe une fonction déjà toute prête : circle. Au minimum, nous devons passer à celle-ci le rayon de notre cercle. De plus, nous pouvons aussi lui passer un angle (extent) qui permet de tracer uniquement une partie du cercle, ainsi qu’un nombre (steps) qui correspond au nombre d’étapes pour tracer. L’orientation du crayon a des conséquences sur la manière dont le cercle sera tracé. Pour mieux comprendre, voyons ce que ça peut donner :

turtle.circle(120)  #Trace un cercle de rayon 120px
turtle.circle(70, 180)  #Trace un demi-cercle de rayon 70px
turtle.circle(90, steps = 8)  #Trace un octogone de longueur 90px
turtle.circle(40, 180, 4)  #Trace la moitié d'un octogone de longueur 40px

Voici un exemple de code pour afficher cinq cercles du plus petit au plus grand, avec pour centre l’origine du repère :

Code :

import turtle

if __name__ == "__main__":
    rayon, ecart = 50, 20
    for i in range(5):
        turtle.up()
        turtle.goto(0, -rayon)
        turtle.down()
        turtle.circle(rayon)
        rayon += ecart  #Augmente la valeur de rayon
    turtle.up()
    turtle.home()
    turtle.exitonclick()

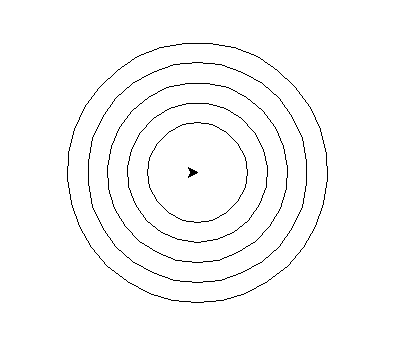
Voilà, nous savons désormais dessiner des figures simples. Dans la section suivante, nous allons complexifier nos figures.

Un dessin plus complexe (1)

Grâce à ce que nous venons d’apprendre, nous pouvons désormais réaliser des figures plus complexes, comme le montre l’image suivante par exemple. Pour réaliser cela, j’ai utilisé deux fonctions que nous n’avons pas encore vues. Tout d’abord, la fonction position, qui ne prend aucun paramètre et retourne, comme son nom l’indique, la position du crayon. Ensuite, j’ai aussi fait appel à la fonction distance qui prend en paramètre les coordonnées x et y d’un point et qui retourne la distance entre le curseur et ce point. De cette manière, j’ai pu connaître facilement la distance entre le centre du dessin, le point (0, 0) et le coin des petits carrés par lesquels je souhaitais faire passer le cercle : c’est-à-dire le rayon. Remarquez que le dessin a pour centre le centre du repère.

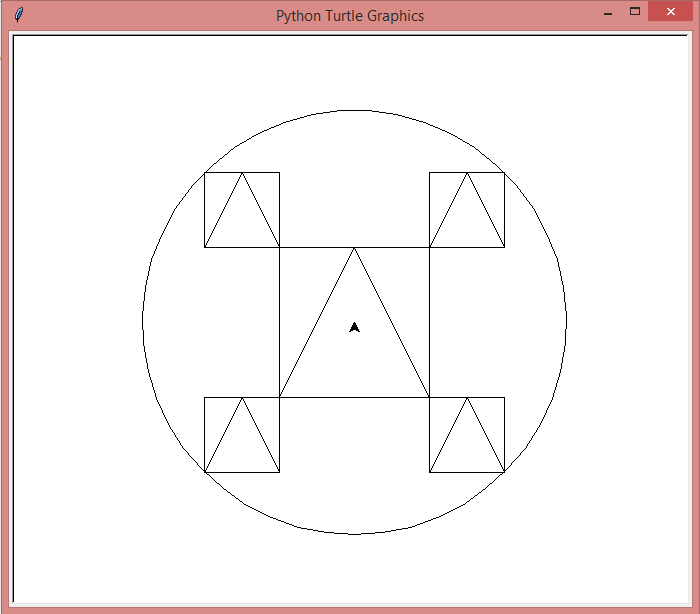
Concernant le code, nous commençons par tracer le grand carré, puis les quatre petits, et nous terminons par le cercle. L’ensemble a pour centre le point d’origine du repère. Pour tracer chaque carré, nous nous plaçons à son coin bas gauche. Les commentaires vous aideront à comprendre. Si vous avez du mal, n’hésitez pas à prendre une feuille de papier et un crayon pour vous aider à visualiser.

Code :

import turtle

def deplacer_sans_tracer(x, y = None):
    """Fonction pour se déplacer à un point sans tracer"""
    turtle.up()
    if (isinstance(x, tuple) or isinstance(x, list)) and len(x) == 2:
        turtle.goto(x)
    else:
        turtle.goto(x, y)
    turtle.down()

def triangle_dans_carre(long_carre):
    """Fonction pour tracer un triangle à l'intérieur du carré"""
    #On prend la position du curseur qui est sur le coin bas gauche
    pos_coin_bg = turtle.position()
    #On trace les deux traits restants, la base étant déjà faite
    turtle.goto(pos_coin_bg[0]+long_carre/2, pos_coin_bg[1]+long_carre)
    turtle.goto(pos_coin_bg[0]+long_carre, pos_coin_bg[1])

def carre_avec_triangle(longueur):
    """Fonction pour tracer un carré avec un triangle à l'intérieur"""
    for i in range(4):
        turtle.forward(longueur)
        turtle.left(90)
    triangle_dans_carre(longueur)

if __name__ == "__main__":
    #On initialise les longueurs du grand carré et des petits carrés
    longueur_1, longueur_2 = 150, 75
    #On se positionne au coin bas gauche de notre futur grand carré
    deplacer_sans_tracer(-longueur_1/2, -longueur_1/2)
    #On le dessine
    carre_avec_triangle(longueur_1)
    #On prépare les valeurs des coin bas gauche des petits carrés
    coins = [(longueur_1/2, longueur_1/2),
             (-longueur_1/2-longueur_2, longueur_1/2),
             (-longueur_1/2-longueur_2, -longueur_1/2-longueur_2),
             (longueur_1/2, -longueur_1/2-longueur_2)]
    #On dessine notre quatre petits carrés
    for coin in coins:
        deplacer_sans_tracer(coin)
        carre_avec_triangle(longueur_2)
    #On retourne au centre de notre dessin
    deplacer_sans_tracer(0, 0)
    #On prend la distance entre le centre et le coin par lequel le cercle passera
    rayon = turtle.distance(longueur_1/2+longueur_2, longueur_1/2+longueur_2)
    #On se déplace et on trace notre cercle
    deplacer_sans_tracer(0, -rayon)
    turtle.circle(rayon)
    #On retourne à la maison, et on prend un angle de 90°
    deplacer_sans_tracer(0, 0)
    turtle.left(90)
    turtle.exitonclick()

Les points

La fonction dot nous permet d’afficher un point dans le canvas. Pour cela, nous pouvons passer en paramètre le diamètre du point, et nous pouvons aussi, si le cœur nous en dit, passer une couleur. Si nous ne lui passons rien, le point aura un diamètre par défaut et la couleur de traçage du curseur (noir par défaut). Nous étudierons le coloriage plus en détails dans la partie suivante.

turtle.dot(100, 'red')  #Imprime un point rouge d'un diamètre de 100px
turtle.dot(50, 'yellow')  #Imprime un point jaune d'un diamètre de 50px
turtle.dot(25)  #Imprime un point noir d'un diamètre de 25px

Remarquons que si nous avions imprimé les points dans l’ordre inverse, nous n’aurions vu que le rouge puisque celui aurait masqué le jaune qui lui-même aurait masqué le noir. Nous pouvons aussi noter qu’un point sera tracé même si le crayon est levé.

Puisque comme d’habitude, rien ne nous empêche de jouer avec ce que nous apprenons, voici un programme qui imprime dix points de plus petit en plus grand en allant de gauche à droite et qui ont une couleur différente :

Code :

import turtle
from random import randint

COULEURS = ['black', 'grey', 'brown', 'orange', 'pink', 'purple',
            'red', 'blue', 'yellow', 'green']

if __name__ == "__main__":
    turtle.setup(650, 100)
    diametre = 15
    turtle.up(); turtle.setx(-turtle.window_width()/2+2*diametre); turtle.down()
    #Pour le nombre de couleurs disponibles
    for i in range(len(COULEURS)):
        #On choisit un couleur aléatoirement
        index_choisi = randint(0, len(COULEURS)-1)
        #On imprime un point de cette couleur
        turtle.dot(diametre, COULEURS[index_choisi])
        #On supprime la couleur choisie pour éviter de la rechoisir
        del COULEURS[index_choisi]
        #On met à jour le diamètre et on se déplace pour le prochain point
        diametre += 5; turtle.up(); turtle.fd(1.5*diametre); turtle.down()
    turtle.exitonclick()

Les tampons

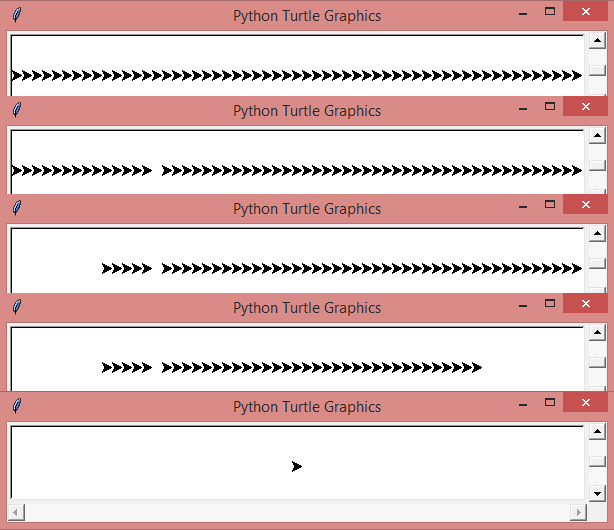
Les points, ce n’est pas tout ! Nous pouvons aussi, de la même manière, imprimer la forme du curseur avec stamp. Cette fonction ne prend aucun paramètre et retourne l’identifiant du tampon. Ce dernier nous sert à supprimer le tampon de la fenêtre en le passant à clearstamp. Nous pouvons aussi supprimer plusieurs tampons de l’écran en fournissant un nombre à clearstamps, voire tous en ne lui passant aucune valeur ou None. Voici ci-dessous un exemple d’utilisation illustré :

id_tampons = []
#L'opération suivante est répétée à maintes reprises tout en se déplaçant
id_tampons.append(turtle.stamp())  #Tamponne et on enregistre l'identifiant
turtle.clearstamp(id_tampons[14])  #Supprime le 15ème tampon
turtle.clearstamps(9)  #Supprime les 9 premiers tampons
turtle.clearstamps(-10)  #Supprime les 10 derniers tampons
turtle.clearstamps()  #Supprime tous les tampons restants

Un dessin plus complexe (2)

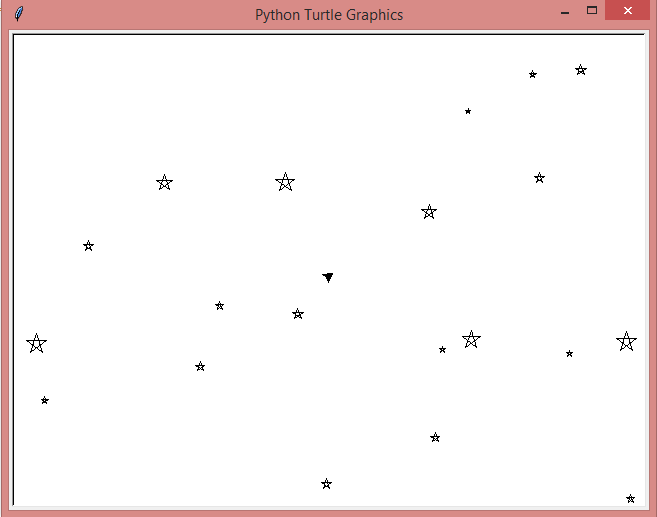
Voici un autre exemple un peu plus complexe. Ici, nous dessinons un ciel étoilé. Pour ce faire, nous avons codé une fonction etoile qui se charge de tracer une étoile d’une longueur donnée, et nous allons nous en servir dans la boucle principale, tout en veillant à ce que l’étoile ne soit pas dessinée hors de notre fenêtre. Nous pourrions améliorer le code pour éviter qu’une étoile soit tracée par dessus une autre par exemple.

import turtle
from random import randint

LARGEUR, HAUTEUR = 640, 480
LONGUEUR_MIN, LONGUEUR_MAX = 5, 20

def deplacer_sans_tracer(x, y = None):
    """Fonction pour se déplacer à un point sans tracer"""
    turtle.up()
    if (isinstance(x, tuple) or isinstance(x, list)) and len(x) == 2:
        turtle.goto(x)
    else:
        turtle.goto(x, y)
    turtle.down()
        
def etoile(longueur):
    """Fonction pour dessiner une étoile"""
    turtle.setheading(180-2*72)
    for i in range(5):
        turtle.forward(longueur)
        turtle.left(180-180/5)
        
if __name__ == "__main__":
    turtle.setup(LARGEUR, HAUTEUR)
    turtle.speed(0) #Met la vitesse de traçage la plus rapide
    nb_etoiles, longueur_etoile = 20, 0
    for i in range(nb_etoiles):
        longueur_etoile = randint(LONGUEUR_MIN, LONGUEUR_MAX)
        deplacer_sans_tracer(randint(-LARGEUR//2+LONGUEUR_MAX//2, LARGEUR//2-LONGUEUR_MAX),
                             randint(-HAUTEUR//2+LONGUEUR_MAX//2, HAUTEUR//2-LONGUEUR_MAX))
        etoile(longueur_etoile)
    deplacer_sans_tracer(0, 0)
    turtle.exitonclick()

Voilà, j’espère que vous avez suivi avec attention, car c’est le moment de mettre tout cela en pratique !

Nous voilà aux travaux pratiques de cette partie ! C’est le moment de vérifier que vous savez dessiner avec ce que nous avons appris. Pour ce faire, il y aura deux exercices où il faudra coder le programme permettant de reproduire le dessin (ne vous souciez pas des longueurs). Si vous êtes bloqué, n’hésitez pas à retourner voir ce que nous avons précédemment pour vous aider et à procéder par étapes. Enfin, lors du troisième exercice, nous nous intéresserons au Flocon de Von Koch.

Exercice 1

Voici la première figure à reproduire :

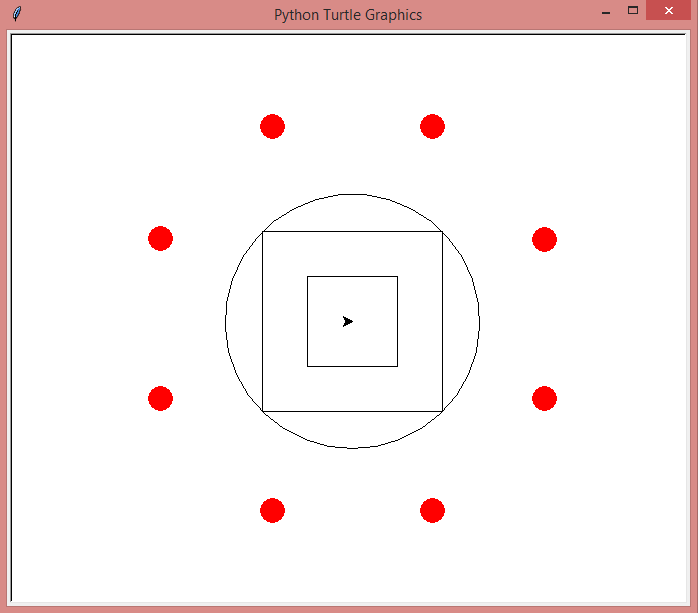
La correction :

import turtle

def deplacer_sans_tracer(x, y = None):
    """Fonction pour se déplacer à un point sans tracer"""
    turtle.up()
    if (isinstance(x, tuple) or isinstance(x, list)) and len(x) == 2:
        turtle.goto(x)
    else:
        turtle.goto(x, y)
    turtle.down()
        
def carre(longueur):
    """Fonction pour tracer un carré depuis le coin bas gauche"""
    for nb_cote in range(4):
        turtle.forward(longueur)
        turtle.left(90)

def point_octogone(longueur, diametre = 5, couleur = 'black'):
    """Fonction pour faire les points des sommets d'un octogone"""
    for nb_cote in range(8):
        turtle.dot(diametre, couleur)
        turtle.up(); turtle.forward(longueur); turtle.down()
        turtle.left(360/8)
        
if __name__ == "__main__":
    #Deux carrés
    longueurs_carre = [90, 180]
    for longueur in longueurs_carre:
        deplacer_sans_tracer(-longueur/2,-longueur/2)
        carre(longueur)
    #Cercle
    rayon = turtle.distance(0,0)  #nous sommes alors sur le coin bas gauche
    deplacer_sans_tracer(0, -rayon)
    turtle.circle(rayon)
    #Octogone de point
    deplacer_sans_tracer(-1.25*rayon/2, -1.25*rayon-30)
    point_octogone(1.25*rayon, 25, 'red')
    #Retour maison
    deplacer_sans_tracer(0, 0)
    turtle.exitonclick()

Exercice 2

Voici la seconde figure à reproduire :

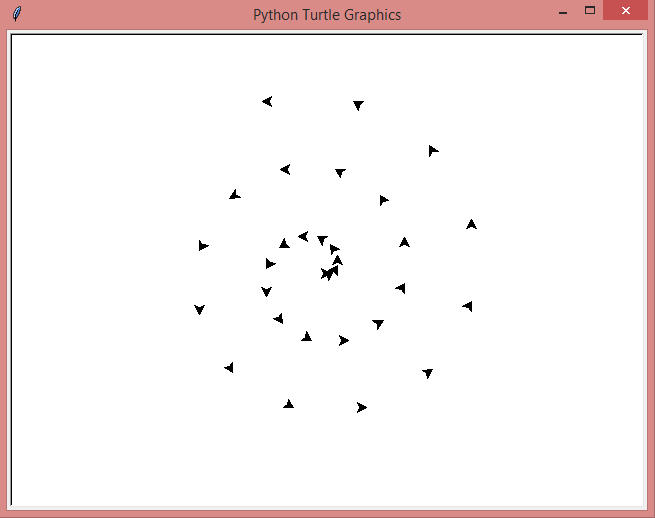
La correction :

import turtle

LARGEUR, HAUTEUR = 640, 480
        
if __name__ == "__main__":
    turtle.setup(LARGEUR, HAUTEUR)
    turtle.speed("fast") #Met la vitesse de traçage à rapide
    ecart = 4
    for i in range(30):
        turtle.stamp()
        turtle.left(30)
        turtle.up(); turtle.forward(ecart); turtle.down()
        ecart += 3
    turtle.exitonclick()

Exercice 3 : Flocon de Von Koch

Un flocon de Von Koch est l’ensemble de trois courbes de Von Koch constituant chaque côté du triangle équilatéral initial. Vous pouvez trouver plus d’explication à propos de cette figure et de sa construction ici.

À travers cet exercice, il va falloir faire une fonction pour dessiner un flocon de Von Koch en fonction de la longueur des côtés du triangle ainsi que du nombre d’étapes permettant choisir le nombre de pics de notre flocon (par exemple, avec 0 et une longueur non nulle, nous avons juste un triangle équilatéral). Cet exercice étant un peu plus complexe, je vous conseille de découper votre progression ainsi : tout d’abord, essayez de programmer une fonction réalisant une courbe de Von Koch selon les paramètres précédemment mentionnés, puis, dans un second temps, réalisez une fonction pour tracer un flocon selon les paramètres.

La correction :

import turtle
 
def courbe_koch(longueur, etape):
    """Fonction récursive pour dessiner une courbe de Von Koch
    (une fonction récursive étant une fonction s'appelant elle-même"""
    if etape == 0:
        turtle.forward(longueur)
    else:
        courbe_koch(longueur/3, etape-1)
        turtle.left(60)
        courbe_koch(longueur/3, etape-1)
        turtle.right(120)
        courbe_koch(longueur/3, etape-1)
        turtle.left(60)
        courbe_koch(longueur/3, etape-1)
 
def flocon_koch(longueur, etape):
    """Fonction pour dessiner un flocon de Von Koch
    depuis le coin haut gauche"""
    for i in range(3):  #Pour chaque côté du triangle initial
        courbe_koch(longueur, etape)  #Courbe de Von Koch
        turtle.right(120)

if __name__ == "__main__":
    flocon_koch(100, 3)

Voilà, la récursivité s’appliquant bien à ce genre de figure, nous avons une fonction récursive pour tracer une courbe de Von Koch, puis une fonction traçant un flocon de Von Koch à l’aide de cette première.