Vous avez sans doute déjà étudié des morceaux de code comprenant des opérateurs assez particuliers. Par exemple, en C, peut-être êtes vous restés perplexes devant des enchevêtrements de &, |, ^ ou ~ ? Si c'est le cas, ce sont les opérateurs bit à bit qui vous ont posé problème. Vous vous demandez à quoi ils servent ? Eh bien, ce tutoriel va vous l'expliquer.
Dans ce cours, nous allons voir à quoi servent les instructions bit à bit et quelques autres du même tonneau. Souvent présentes dans nos processeurs, celles-ci paraissent nettement moins utiles que les sempiternelles additions, soustractions, lectures ou écritures en mémoire, par exemple ; nous allons vous prouver le contraire.
Attention toutefois : vous devez être familier avec l'encodage des entiers et des flottants. Si vous ne savez ce qu'est un complément à 2 ou à 1, ou encore ce que constitue un nombre flottant IEEE754, revenez plus tard. De même, vous devrez faire face à des descriptions de circuits électroniques dans ce qui suivra. Vous voilà prévenus !
Toujours là ? Maintenant, fermez les yeux et entrez dans le arcanes du bit twiddling, la manipulation de bits avec des opérations bas niveau.
- Instructions bit à bit et décalages
- Les subtilités de l'instruction XOR
- Les puissances de deux
- Comptage de bits
- Arithmétique et Branch free code
- Champs de bits
- Bit de parité
Instructions bit à bit et décalages
Ces instructions travaillent souvent sur des nombres entiers. Comme vous le savez, dans notre ordinateur, ces nombres sont stockés sous la forme de suites de bits d'une longueur fixe. Et bien ces instructions bit à bit vont modifier directement l'écriture binaire d'un nombre. elles travaillent directement sur la suite de bits correspondante. Il en existe de deux types : les instructions bit à bit, et les instructions de décalage.
Instructions logiques
Les instructions logiques les plus courantes sont au nombre de 4. On trouve ainsi :
- le NOT bit à bit ;
- le AND bit à bit ;
- le OR bit à bit ;
- le XOR bit à bit.
Toutes ces instructions vont travailler sur des bits individuels d'un ou de deux nombres, et leur faire subir une opération bien précise. Le fonctionnement de cette opération peut être définie par ce qu'elle fait sur un bit, son comportement étant résumé dans un tableau qu'on appelle la table de vérité.
NOT
Le NOT bit à bit va prendre un nombre entier, et va inverser tous les bits de ce nombre. Les zéros deviennent des 1, et les 1 deviennent des zéros.
Exemple : le nombre 01110011 va devenir 10001100.
La table de vérité du NOT est celle-ci :
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Le NOT d'un nombre sera noté comme ceci : $\overline{x}$
On peut remarquer qu'inverser deux fois de suite un bit redonne le bit initial. Autrement dit, $\overline{\overline{a}} = a$.
Cette opération est assez simple à comprendre, mais son interprétation change selon que l'on utilise des entiers non-signés, encodés en complément à 1, etc.
Pour un entier en complément à 1, le NOT sert à obtenir l'inverse d'un nombre.
Pour un entier en complément à deux, le NOT ne donne pas exactement l'inverse d'un nombre. L'inverse d'un entier x, codé en complément à deux, est égal à :
$\overline{x} + 1$
Ce qui est équivalent à :
$\overline{x - 1}$
Pour un entier non-signé, le NOT va donner un résultat un peu plus surprenant. Supposons que notre entier x soit codé sur N bits. $\overline{x}$ sera alors égal à $2^N - x - 1$. Cela peut se comprendre facilement. Prenez un entier $X$ et ajoutez lui $\overline{x}$. Vous allez vous retrouver avec un entier de $N$ bits, tous à 1. Or, un entier de $N$ bits qui valent tous 1 a pour est égal à $2^N - 1$.
AND
Vient ensuite le AND bit à bit. Ce AND bit à bit va prendre deux nombres. Sur ces deux nombres, il va prendre les bits qui sont à la même place et va effectuer dessus une petite opération qui donnera le bit du résultat.
Cette opération est un simple AND binaire. Ce AND binaire prend deux bits, A et B, et fonctionne comme ceci :
| A | B | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Cet opérateur AND bit à bit est symbolisé comme ceci : $a.b$
Exemple : $1100.1010 = 1000$
L'instruction AND bit à bit est commutative : $a.b = b.a$
Elle est aussi associative : $(a.b).c = a.(b.c)$
Elle est aussi distributive avec le OR bit à bit : $(a+b).c = (c.b)+(c.a)$
On peut aussi remarquer qu'elle dispose de la propriété d'idempotence : $a.a = a$
Petite remarque : $a.0 = 0$
De plus, $a . \overline{a} = 0$
OR
Vient ensuite le OR bit à bit. Il fonctionne comme le AND bit à bit sauf qu'il effectue un OR binaire entre les bits du nombre. Ce OR binaire prend deux bits, A et B, et fonctionne comme ceci :
| A | B | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Cet opérateur OR bit à bit est symbolisé comme ceci : $a+b$
Exemple : $1100.1010 = 1110$
L'opérateur OR est commutatif : $a+b = b+a$
Il est aussi associatif : $(a+b)+c = a+(b+c)$
Il est aussi distributif avec le AND bit à bit : $(a.b)+c = (c+b).(c+a)$
On peut aussi remarquer qu'il dispose de la propriété d'idempotence : $a+a = a$
Petite remarque : $a+0 = a$
XOR
Vient ensuite le XOR bit à bit. Il fonctionne comme le AND et le OR bit à bit sauf qu'il effectue un XOR binaire entre les bits du nombre. Ce XOR binaire prend deux bits, A et B, et fonctionne comme ceci :
| A | B | Résultat |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Cet opérateur XOR bit à bit est symbolisé comme ceci : $a \oplus b$
Exemple : $1100 \oplus 1010 = 0110$
L'opérateur XOR est commutatif : $a \oplus b = b \oplus a$
Il est aussi associatif : $( a \oplus b ) \oplus c = a \oplus ( b \oplus c )$
Petite remarque : $a \oplus 0 = a$
Instructions de décalages
Ensuite, on trouve les opérations de décalages et de rotation, qui vont décaler les bits d'un nombre d'un certain nombre de rangs. Il en existe plusieurs types.
Décalages logiques
Le décalage logique, aussi appelé logical shift, consiste à décaler tout ses chiffres d'un ou plusieurs crans vers la gauche ou la droite. Lors du décalage, des vides apparaissent dans la représentation binaire du nombre : ceux-ci sont alors remplis avec des zéros.
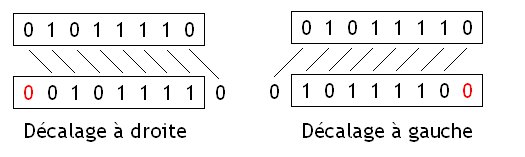
Grâce à ce remplissage par des zéros, un décalage vers la gauche de n rangs est équivalent à une multiplication par $2^{n}$ pour des entiers non-signés ou pour des entiers signés positifs. Même chose pour le décalage vers la droite qui revient à diviser un nombre entier par $2^{n}$. Avec des nombres signés, ce n'est pas le cas : on obtient un résultat qui n'a pas grand sens mathématiquement.
Cette propriété est souvent utilisée par certains compilateurs, qui préfèrent utiliser des instructions de décalages (qui sont des instructions très rapides) à la place d'instructions de multiplication ou de division qui ont une vitesse qui va de moyenne (multiplication) à particulièrement lente (division).
Il faut remarquer un petit détail : lorsqu'on effectue un décalage à droite -, certains bits de notre nombre vont sortir du résultat et être perdus. Cela a une conséquence : le résultat est tronqué ou arrondi. Plus précisément, le résultat d'un décalage à droite de n rangs sera égal à la partie entière du résultat de la division par $2^{n}$.
Décalages arithmétiques
Les décalages arithmétiques sont similaires aux logical shift, à un détail prêt : pour les décalages à droite, le bit de signe de notre nombre n'est pas modifié, et on remplit les vides laissés par le décalage avec le bit de signe.
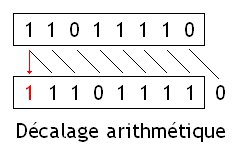
Ces instructions sont équivalentes à une multiplication/division par $2^n$, que le nombre soit signé ou non, à un détail prêt : l'arrondi n'est pas fait de la même façon pour les nombres positifs et négatifs. Pour donner un exemple, $ \frac {9} {2}$ sera arrondi en 4, tandis que $\frac {-9} {2}$ sera arrondi en -5.
Rotations
Les rotations sont identiques aux décalages, à part que les bits qui sortent du nombres sont ceux qui rentrent pour combler les vides.
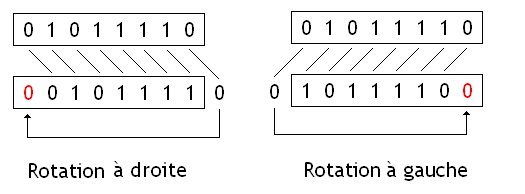
Ces opérations sont très utiles en cryptographie, et sont notamment très utilisées dans certaines algorithmes de chiffrement. Les rotations sont aussi très utiles dans certains particuliers dans lesquels ont doit manipuler des données bits par bits. Par exemple, un calcul du nombre de bits à 1 dans un nombre peut s'implémenter de façon naïve avec des instructions de rotation.
Les subtilités de l'instruction XOR
Dans cette partie, nous allons voir ce qu'il est possible de faire avec l'instruction XOR.
Mise à zéro
Pour commencer, nous allons regarder ce qui se passe lorsque l'on XOR un bit avec lui-même.
Prenons la table de vérité du XOR :
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Dans cette table de vérité, nous allons regarder les deux lignes où A est égal à B.
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0 |
On remarque donc que dans le cas où on XOR un bit avec lui-même, le résultat est toujours zéro.
Cela a une conséquence : appliquez ce que l'on vient de découvrir à un nombre. Si on le XOR avec lui-même, chacun de ses bits sera donc XORé avec lui-même, et sera donc mis à zéro. Conséquence : un nombre XOR lui-même donnera toujours zéro.
$A \oplus A = 0$
Cette propriété est utilisé en assembleur pour mettre à zéro un registre. D'ordinaire, on met un registre à zéro en utilisant une instruction qui charge une constante (ici zéro) dans un registre.
Seul problème : cette constante peut parfois être intégrée directement dans la suite de bits de l'instruction, si celle-ci peut utiliser le mode d'adressage immédiat. Dans ce cas, une dizaine de bits est utilisée pour stocker la constante.
En comparaison, une instruction XOR entre deux registres n'aura pas besoin d’intégrer de constante à coté de son opcode, et prendra moins de place. Sur d'autres processeurs, la constante est lue depuis la mémoire. En comparaison, un XOR entre deux registres ne va rien charger en RAM et est donc plus rapide.
Échange de deux valeurs
Toutefois, cette propriété a aussi des conséquences un peu plus utiles. Prenons le cas de l'échange de deux données, stockées dans une variable ou un registre, peu importe. Logiquement, vous utilisez un registre ou une variable temporaire pour échanger les deux valeurs. Avec le XOR il est possible de faire autrement.
Algorithme
Il est en effet possible d'échanger le contenu de deux registres/variables A et B en effectuant les opérations suivante, dans l'ordre :
- D'abord, on calcule $A \oplus B$, et on stocke le tout dans A.
- Ensuite, on recalcule $A \oplus B$ avec les A et B obtenus à l'étape d'avant, et on stocke le tout dans B.
- Ensuite, on recalcule $A \oplus B$ avec les A et B obtenus à l'étape d'avant, et on stocke le tout dans A.
Pour résumer, voici la liste des opérations à effectuer :
- $A = A \oplus B$
- $B = A \oplus B$
- $A = A \oplus B$
Toutefois il faut faire attention : ni A, ni B ne doivent valoir zéro. Si un seul d'entre eux vaut zéro, et pas l'autre, l'algorithme du dessus ne marche pas. Dans ce cas, les deux données/registres sont mises à zéro. Ce qui n'est pas le but recherché.
Principe
Mais comment cela fonctionne ? Pour cela, rien de plus simple : il suffit de regarder à chaque étape ce que l'on trouve dans A et dans B.
| Etape | A | B |
|---|---|---|
| Etape préliminaire | $A$ | $B$ |
| Première étape | $A \oplus B$ | $B$ |
| Seconde étape | $A \oplus B$ | $(A \oplus B) \oplus B$ |
| Troisième étape | $(A \oplus B \oplus B) \oplus (A \oplus B)$ | $(A \oplus B) \oplus B$ |
Vu que XOR est associatif, commutatif, distributif, on peut alors simplifier ces équations, en déplacant les parenthèses, et en regroupant certains termes.
| Etape | A | B |
|---|---|---|
| Etape préliminaire | $A$ | $B$ |
| Première étape | $A \oplus B$ | $B$ |
| Seconde étape | $A \oplus B$ | $A \oplus (B \oplus B)$ |
| Troisième étape | $(A \oplus A) \oplus (B \oplus B) \oplus B$ | $A \oplus (B \oplus B)$ |
Si on se rappelle que $X \oplus X = 0$, les expressions entre parenthéses se simplifent en zéro, ce qui donne :
| Etape | A | B |
|---|---|---|
| Etape préliminaire | $A$ | $B$ |
| Première étape | $A \oplus B$ | $B$ |
| Seconde étape | $A \oplus B$ | $A \oplus 0$ |
| Troisième étape | $0 \oplus 0 \oplus B$ | $A \oplus 0$ |
Ce qui se simplifie en :
| Etape | A | B |
|---|---|---|
| Etape préliminaire | $A$ | $B$ |
| Première étape | $A \oplus B$ | $B$ |
| Seconde étape | $A \oplus B$ | $A$ |
| Troisième étape | $B$ | $A$ |
Comme on le voit, nos données ont bien étés inversées.
Mise en garde
Je tiens toutefois à apporter une précision. Sur un grand nombre de processeur, échanger le contenu de deux variables/registres/adresses en utilisant un XOR est BEAUCOUP plus lent que d'utiliser un registre ou une variable temporaire. Les raisons sont multiples, et je ne me sens pas capable de parler de renommage de registre, ou de datapath dans ce tutoriel. Vous allez donc devoir me croire : l'échange avec des XOR est plus lent. Ne l'utilisez jamais…
Listes XOR doublements chainées
Cette propriété est aussi utilisée pour créer des listes doublement chainées plus économes en mémoire. Une liste doublement chainée normale stocke deux pointeurs : un vers le nœud suivant, et un vers le nœud précédent.
| Noeud 1 | Noeud 2 | Noeud 3 | … |
|---|---|---|---|
| A | B | C | … |
| ptr_B | ptr_C | ptr_D | … |
| NULL | ptr_A | ptr_B | … |
Les XOR linked list permettent de ne pas stocker les deux pointeurs : à la place ils stockent un seul pointeur. Celui-ci contient le XOR entre le pointeur vers le prochain nœud, et le pointeur vers le nœud précédent.
| Noeud 1 | Noeud 2 | Noeud 3 | … |
|---|---|---|---|
| A | B | C | … |
| ptr_B | ptr_C⊕ptr_A | ptr_B⊕ptr_D | … |
Ainsi, on gagne un petit peu de mémoire : au lieu de stocker deux pointeurs, on n'en stocke plus qu'un seul. La consommation mémoire est aussi nidentique à celle d'une liste simplement chainée.
Mais comment faire pour traverser cette liste ? Rien de plus simple, mais nous allons commencer par comprendre quel principe se cache derrière ces listes.
Dans ce qui suit :
- le pointeur sur le nœud précédent sera noté Prev
- le pointeur contenu dans le nœud actuellement visité est appellé Ptr ;
- le pointeur vers le nœud suivant sera noté Next.
Pour rappel, le pointeur stocké dans le nœud est égal au XOR entre $Prev$ et le $Next$.
Nous allons commencer par voir un parcours commençant par le début de la liste vers la fin de celle-ci. Comment obtenir le pointeur vers le prochain élément? Supposons que dans ce cas, nous XORions le pointeurs vers l’élément précédent avec le pointeur stocké dans le nœud.
$Ptr = Prev \oplus Next$
Supposons que je veuille XORer $Prev$ et $Ptr$
$Prev \oplus Ptr = Prev \oplus Prev \oplus Next$
Ce qui se simplifie en :
$Prev \oplus Ptr = Next$
Ainsi, $Prev \oplus Ptr$ nous donne l'adresse du prochain nœud dans la liste. En conclusion, pour obtenir l’élément suivant, il suffit d'effectuer un XOR entre l'adresse du nœud précédemment visité et le pointeur stocké dans le nœud.
Le même raisonnement peut s'adapter dans le cas où l'on parcours la liste dans l'autre sens. $Next \oplus Ptr$ donne $Prev$. Donc, dans ce cas, on doit XORer le pointeur de l’élément précédemment visité (qui correspond alors à Next) avec le pointeur stocké dans le nœud. Malheureusement, cela ne marche évidemment que si l'on parcourt la liste dans un seul sens.
Les puissances de deux
Quand on travaille en binaire, il arrive souvent qu'on ait à manipuler des puissances de deux. Et quand il s'agit d'opérations bit à bit, on n'y coupe pas.
Test
Tout d'abord, nous allons regarder comment vérifier qu'un nombre est bien une puissance de deux.
On peut remarquer une chose : en binaire, $2^n$ s'écrit sous la forme d'un nombre dont seul le n-ième bit est à 1.
| Puissance de deux | Écriture binaire |
|---|---|
| 1 | 0000 0001 |
| 2 | 0000 0010 |
| 4 | 0000 0100 |
| 8 | 0000 1000 |
| 16 | 0001 0000 |
| 32 | 0010 0000 |
| 64 | 0100 0000 |
| 128 | 1000 0000 |
Par contre, $2^n-1$ est un nombre dont tous les bits qui précédent le n-ième bit sont à 1.
| Puissance de deux | Écriture binaire |
|---|---|
| 0 | 0000 0000 |
| 1 | 0000 0001 |
| 3 | 0000 0011 |
| 7 | 0000 0111 |
| 15 | 0000 1111 |
| 31 | 0001 1111 |
| 63 | 0011 1111 |
| 127 | 0111 1111 |
Si on regarde bien, il n'y a pas de bit qui soit à 1 à la fois dans l'écriture de $2^n$, et dans celle de $2^{n-1}$.
Cela a une conséquence : si on effectue un AND entre ces deux nombres, les bits qui sont à zéro dans un nombre vont annuler les 1 qui sont dans l'autre. En clair : $2^n . 2^n-1 = 0$.
Ce qui signifie que si x est une puissance de deux, alors $x . (x-1) = 0$. Et la réciproque est vraie : si $x . (x-1) = 0$, alors x est une puissance de deux.
Attention toutefois : avec cette technique, zéro est considéré comme une puissance de deux. Faites donc attention.
2^n - 1 immédiatement supérieur
Supposons que je veuille arrondir un nombre à la puissance de deux qui lui est immédiatement supérieure. Par exemple, je veux arrondir 5 à 8. Ou 25 à 31. Ou encore 250 à 255. Bref… Comment dois-je m'y prendre ?
Pour cela, nous allons faire une petite remarque. Prenons un nombre, que l'on va nommer N. Dans ce qui va suivre, ce N vaudra 0010 1101, pour l'exemple.
Comme vous le voyez, ce nombre est de la forme 001X XXXX, avec X qui vaut zéro ou 1 selon le bit.
Maintenant, regardons ce que vaut N OR (N >> 1).
| opération | nombre |
|---|---|
| 001X XXXX | |
| OR | 0001 XXXX |
| = | 0011 XXXX |
Ensuite, regardons ce que vaut N OR (N >> 1) OR (N >> 2).
| opération | nombre |
|---|---|
| 001X XXXX | |
| OR | 0001 XXXX |
| OR | 0000 1XXX |
| = | 0011 1XXX. |
Vous commencez à comprendre ? Les bits qui sont à droite du 1 le plus à gauche se remplissent progressivement avec des 1, au fur et à mesure des décalages. Si on pousse le bouchon encore plus loin, on se retrouvera avec un nombre dont tous les bits à droite du 1 le plus à gauche seront tous des 1. Un tel nombre est un nombre de la forme $2^n-1$. Pour être plus précis, il s'agit du nombre de la forme $2^n-1$ immédiatement supérieur à N.
On doit donc effectuer un grand nombre de décalages pour mettre à 1 tous les bits à droite. Si vous avez un nombre de n bits, vous devez effectuer n décalages et ORer le tout.
Dans notre exemple, on a un nombre de 8 bits, ce qui donne : N OR (N >> 1) OR (N >> 2) OR (N >> 3) OR (N >> 4) OR (N >> 5) OR (N >> 6) OR (N >> 7) OR (N >> 8), etc. Le résultat est :
| opération | nombre |
|---|---|
| 001X XXXX | |
| OR | 0001 XXXX |
| OR | 0000 1XXX |
| OR | 0000 01XX |
| OR | 0000 001X |
| OR | 0000 0001 |
| OR | 0000 0000 |
| = | 0011 1111 |
Ce qui donne le nombre de la forme $2^n-1$ immédiatement supérieur.
2^n - 1 immédiatement inférieur
On peut calculer le nombre de la forme $2^n-1$ immédiatement inférieur en calculant le nombre de la forme $2^n-1$ immédiatement supérieur, et en le décalant d'un cran vers la droite.
Ou plus simplement, il suffit de faire le calcul suivant :
(N >> 1) OR (N >> 2) OR (N >> 3) OR (N >> 4) OR (N >> 5) OR (N >> 6) OR (N >> 7) OR (N >> 8) OR …
Puissance de deux immédiatement supérieure
Calculer la puissance de deux immédiatement supérieure est facile : il suffit de calculer le nombre de la forme $2^n-1$ immédiatement supérieur, et de lui ajouter 1.
Puissance de deux immédiatement inférieure
Pour obtenir la puissance de deux immédiatement inférieure, il suffit d'adapter le code du dessus. Pour cela, on commence par calculer le nombre de la forme $2^n - 1$ immédiatement supérieur. Ensuite, on applique la formule suivante au résultat :
$x - (x >> 1)$
Arrondir au multiple de $2^n$ le plus proche
Ensuite, on peut vouloir arrondir un nombre au multiple de $2^n$ le plus proche. Pour cela, il y a deux types d'arrondis : vers le multiple de $2^n$ immédiatement supérieur, ou le multiple immédiatement inférieur.
Pour le multiple immédiatement supérieur, prenons un exemple. Je souhaite arrondir 46 au multiple de 8 immédiatement supérieur : 46 sera arrondi à 48 (8 6). Si j'avais voulu arrondir au multiple immédiatement inférieur, j'aurais obtenu 40 (85).
Le plus simple, c'est arrondir au multiple de $2^n$ immédiatement inférieur. Pour cela, il suffit de mettre les n bits les plus à droite à 0. Si on regarde bien, cela revient à appliquer un AND entre le nombre à arrondir et une constante bien précisé. Cette constante vaut : $2^n - 1$. Effectuer l'arrondi demande donc de faire ce calcul :
$ X ~ AND (2^n - 1) $
Exemple : je veux arrondir x au multiple de 8 inférieur. Dans ce cas, je dois faire :
$x . 1111...111000$
Pour arrondir au multiple de x immédiatement supérieur, on peut procéder de différentes façons. On peut arrondir au multiple inférieur, et ajouter $2^n$. Une autre solution consiste à mettre les n bits de poids faible à 1 dans le nombre à arrondir, avant d'ajouter 1. Ainsi, pour arrondir un nombre X, je dois effectuer le calcul suivant :
$ ( X ~ OR (2^n - 1) ) + 1 $
Comptage de bits
Il arrive qu'on aie besoin de compter les bits d'un certain nombre. Par exemple, certaines application en cryptographie ont besoin de savoir combien de bit sont à 1 dans un nombre. Même chose pour la détection ou correction d'erreurs de transmission entre deux composants électroniques. Dans ce qui va suivre, nous allons voir quelles sont les opérations de comptage les plus courantes, et comment les implémenter en logiciel et en matériel.
Population Count
La population count d'un nombre est le nombre de ses bits qui sont à 1. Cette population count est aussi appelé poids de Hamming dans certaines situations. Ce calcul est souvent effectué quand on cherche à vérifier l'intégrité de données transmises ou stockées sur un support pas trop fiable. Il est à la base d'un grand nombre de code de détection ou de correction d'erreurs usuels.
Pour la calculer, on peut utiliser un dispositif matériel ou logiciel. En logiciel, la solution la plus simple consiste à utiliser une boucle avec quelques opérations bit à bit. Mais cette solution est inefficace. A la place on doit ruser.
Supposons que j'ai un nombre de $N$ bits. Si je découpe ce nombre en deux morceaux, je sais que sa population count est égale à la somme des population count des deux morceaux. Et je peux appliquer le même raisonnement sur chaque morceau. Au final, je finirais par avoir des morceaux de plus en plus petits, jusqu'à obtenir des morceaux de 1 bit. Dans ce cas, je sais que la population count d'un morceau de 1 bit vaut 1 si le bit est à 1, et zéro s'il vaut zéro. En clair : la population count de 1 bit vaut…le bit en question.
Cette procédure de découpage d'un nombre en morceaux est utilisé dans tout les circuits ou algorithmes efficaces de calcul de population count.
Matériel
Par exemple, on peut créer un circuit de calcul de population count en utilisant des couches d'additionneurs reliés en série.

Logiciel
En logiciel, ce principe de décomposition s'applique aussi. Mais la manière de l'appliquer est à l'origine d'un des plus beau algorithme de bit twiddling au monde. Pour illustrer l'algorithme, nous allons prendre l'exemple d'un nombre sur 8 bits. Nous allons noter N le nombre dont on recherche la population count.
Première étape : l'algorithme commence par grouper les bits du nombre par groupes de deux et les additionne. Pour cela, l'algorithme va avoir besoin de deux variables.
La première variable va stocker tous les bits à une position paire. Les autres bits sont mis à zéro. En clair :
variable1 = N . 01010101.
L'autre stockera les bits en position impaire, les autres sont mis à zéro. En clair :
variable2 = N . 10101010.
Puis, un petit décalage va mettre les bits des deux variables sur la même colonne.
variable2 >> 1
Enfin, on additionne ces deux variables.
variable 1 + variable 2.
Résumé de la première étape :
- variable1 = N . 01010101
- variable2 = (N . 10101010) >> 1
- variable 1 + variable 2.
Cette étape effectue la même chose que la première couche d'additionneur dans le circuit du dessus. Elle groupe les bits par groupes de deux, et les additionne. Pour comprendre comment, nous allons regarder de plus prêt ce qui se passe sur les bits de N. Supposons que notre nombre N aie 8 bits, notés comme ceci :
a7 a6 a5 a4 a3 a2 a1 a0
Variable2 + Variable1 donnera ceci :
| Variable | groupe de deux bits | groupe de deux bits | groupe de deux bits | groupe de deux bits |
|---|---|---|---|---|
| variable1 | 0 a6 | 0 a4 | 0 a2 | 0 a0 |
| variable 2 >> 1 | 0 a7 | 0 a5 | 0 a3 | 0 a1 |
| total | a6+a7 | a4+a5 | a2+a3 | a0+a1 |
La seconde étape est similaire, si ce n'est qu'elle isole les groupes de deux bits crées à l'étape précédente deux à deux, et les additionne.
- variable1 = N . 00110011
- variable2 = (N . 11001100) >>2
- variable 1 + variable 2.
| Variable | groupe de 4 bits | groupe de 4 bits |
|---|---|---|
| variable1 | 00 a4+a5 | 00 a0+a1 |
| variable 2 >> 1 | 00 a6+a7 | 00 a2+a3 |
| total | a4+a5+a6+a7 | a0+a1+a2+a3 |
Et on, poursuit ainsi de suite, jusqu'à obtenir la population count de notre nombre. Dans notre exemple, une troisième étape suffit pour obtenir le résultat.
Troisième étape :
- variable1 = N . 00001111
- variable2 = (N . 11110000) >> 4
- variable 1 + variable 2.
| Variable | groupe de 8 bits | groupe de 4 bits |
|---|---|---|
| variable1 | 0000 a0+a1+a2+a3 | |
| variable 2 >> 1 | 0000 a4+a5+a6+a7 | |
| total | a0+a1+a2+a3 + a4+a5+a6+a7 |
Petite remarque : dans les calculs du dessus, vous remarquez que le calcul de variable2 et de variable1 ne s'effectuent pas avec les mêmes constantes. Ceci dit, il est possible de bidouiller un petit peu nos calculs pour que ce soit le cas.
Le calcul de variable2 s'effectue avec un AND et un décalage.
- variable2 = (N . 10101010) >> 1
- variable2 = (N . 11001100) >> 2
- variable2 = (N . 11110000) >> 4
Or, il faut savoir que les décalages sont distributifs par rapport au AND. En clair : (a . b) >> n = (a >> n) . (b >> n).
Si on applique cette formule aux équations du dessus, on obtient :
- variable2 = (N >> 1) . (10101010 >>1) = (N >> 1) . 01010101
- variable2 = (N >> 2) . (11001100 >>2) = (N >> 2) . 00110011
- variable2 = (N >> 3) . (11110000 >>4) = (N >> 3) . 00001111
Les constantes utilisées sont exactement les mêmes que celles utilisée dans le calcul de variable1.
Cela a un avantage sur certaines architectures RISC. Il arrive souvent que les architectures RISC utilisent des instructions machines de longueur fixe. Dans ces conditions, les constantes immédiates ont une taille limitée. En conséquence, si une constante dépasse cette taille, elle ne peut pas utiliser le mode d'adressage immédiat. A la place, la constante est placée dans la mémoire, et est chargée dans un registre à chaque utilisation.
Le fait de réutiliser la même constante pour le calcul de variable1 et de variable2 permet ainsi de charger cette constante une seule fois, et la réutiliser depuis le registre lors du calcul de variable2. En utilisant deux constantes différentes, on aurait deux accès mémoire, ce qui aurait été bien plus lent.
Il existe une autre solution logicielle pour calculer la population count d'un nombre. Il suffit d'utiliser un tableau, dans lequel on stocke la population count pour chaque byte. Il suffit ensuite d'utiliser ce tableau pour obtenir la population count de chaque byte d'un nombre, et de les additionner.
Cette technique est beaucoup plus lisible que la précédente, mais elle a le défaut d'effectuer des accès à la mémoire. Or, ces accès mémoires sont des opérations assez lentes. En comparaison, la technique avec les constantes ne fait que des calculs et devrait être plus rapide dans la majorité des situations réalistes.
Find First 1
Maintenant, nous allons voir comment déterminer la position du 1 le plus significatif dans l'écriture binaire du nombre. En clair, la position du 1 le plus à gauche. Mine de rien, ce calcul a une interprétation arithmétique : il s'agit du logarithme en base 2 d'un entier non-signé.
Dans tout ce qui va suivre, nous allons numéroter les bits à partir de zéro : le bit le plus à droite d'un nombre (son bit de poids faible) sera le 0-ème bit.
Nous allons commencer par voir un cas simple : le cas où notre nombre est une puissance de deux. Dans ce cas, un seul bit est à 1 dans notre nombre. Dans ce cas, un nombre dont le n-ième bit est à 1 vaut $2^n$. Pour comprendre pourquoi, on va devoir faire une démonstration par récurrence.
Déjà, on remarque que la propriété est vraie pour $2^0$ : le 0-ème bit du nombre est mis à 1.
Supposons que le fait que cette propriété soit vraie pour n. Regardons ce qui se passe pour n+1.
Dans ce cas, $2^{n+1} = 2^{n} \times 2$.
Ce qui est équivalant à : $2^{n+1} = 2^{n} << 1$.
Donc, si le bit à 1 pour $2^n$ était le n-ième bit, alors le bit à 1 pour $2^{n+1}$ sera cela situé à sa gauche (à cause du décalage). En clair : ce sera le n+1-ème bit.
Maintenant, qu'en est-il pour n'importe quel nombre, et pas seulement les puissances de deux ? Rien de plus simple.
Prenons n'importe quel nombre, écrit en binaire. Si celui-ci n'est pas une puissance de deux, alors il est compris entre deux puissances de deux. Dans ce qui va suivre, nous allons prendre les deux puissances de deux immédiatement inférieure et supérieures à notre nombre. Nous allons les noter inf et sup.
On souhaite obtenir :
$log_2(A)$
On peut penser qu'il suffit de remplacer A par $2^n + 2^{n-1} + 2^{n-2} + ... 2^2 + 2^1 + 2^0$ dans l'équation du dessus. Mais en faisant cela, on ne peut pas trouver le logarithme. Ceci dit, on peut donner une estimation de ce logarithme avec un tout petit peu de réflexion.
On sait que :
$inf < A < sup$
En supposant que inf = $2^n$, on a :
$2^n < A < 2^{n+1}$
Le logarithme d'un nombre est une fonction qui est toujours croissante. C'est à dire que si A > B, alors log(A) > log(B). Il s'ensuit que :
$ log_2 ( 2^n ) < log_2 ( A ) < log_2 ( 2^{n+1} ) $
Le tout se simplifie en :
$ n < log_2 ( A ) < n+1 $
Cette équation nous dit que l'on peut calculer la partie entière du logarithme de A : c'est le nombre n. Que vaut n ? C'est la position du 1 dans la puissance de deux immédiatement inférieure à A. Donc, on en déduit que pour calculer la partie entière du logarithme d'un nombre non-signé, il suffit de calculer la position de son 1 le plus à gauche.
Matériel
Cette opération se calcule très simplement en hardware.
Prenons le cas d'un nombre qui est une puissance de deux : il existe un circuit qui est spécialement conçu pour obtenir la position du bit à 1 d'un tel nombre. Ce circuit est ce qu'on appelle un encodeur. Cet encodeur est un circuit qui répond à plusieurs critères :
- il prend en entrée un nombre de n bits, donc un encodeur possède n entrées ;
- il doit fournir une position codée sur log(n) bits : ce contrôleur a donc log(n) sorties ;
- les entrées sont numérotées de 0 à n-1 ;
- si l'entrée x est à 1 (et seulement celle-ci), alors la sortie sera la représentation binaire du nombre x.
En comptant les bits à partir de zéro, le n-iéme bit du nombre doit être relié à l'entrée numéro n.
Si l'on veut aussi traiter des nombres qui ne sont pas seulement des puissances de deux, on doit modifier l'encodeur. Il devient alors un encodeur à priorité. Fabriquer un tel encodeur à priorité est assez simple : on peut tout simplement écrire sa table de vérité et en déduire le circuit directement. Mais il va de soit qu'effectuer de telles manipulations pour créer des circuits avec un grand nombre d'entrée n'est pas la meilleure des solutions. Il est possible de faire autrement.
La solution la plus élégante est de rajouter un circuit avant l'encodeur qui transforme un nombre en sa puissance de deux immédiatement inférieure ou égale.

Logiciel
En logiciel, cette opération se calcule assez simplement.
Pour traiter les puissances de deux, il suffit de pré-calculer la position du 1 le plus à gauche pour chaque puissance de deux, et de stocker le tout en mémoire : une simple table de hachage, voire un tableau, suffit.
Pour traiter tous les nombres, on peut utiliser un petit morceau de code qui renvoie la puissance de deux immédiatement inférieure, et lire le résultat dans le tableau mentionné au-dessus.
Count leading zeros
Dans un ordinateur, les nombres sont de taille fixe. Un nombre est ainsi stocké sur 8, 16, 32, 64 bits. Si jamais un nombre peut être represénté en utilisant moins de bits que prévu, les bits qui restent sont mis à zéro. Par exemple, sur une architecture 8 bits, le nombre 5 ne sera pas stocké comme ceci :
$101$
Mais comme ceci :
$0000 0101$.
On voit donc que ce nombre contient un certain nombre de zéros non-significatifs. Ces zéros sont placés à gauche du nombre. Plus précisément, notre nombre aura certains de ses bits à 1. Parmi ceux-ci, il y aura un de ces bits qui sera plus à gauche que tous les autres 1. A gauche de ce 1, on peut éventuellement trouver un certain nombre de zéros non-significatifs. L'instruction Count leading zeros a pour objectif de compter ces zéros non-significatifs.
En matériel, cette opération est souvent utilisée dans certaines unités de calcul à virgule flottante, dans les opérations de normalisation et d'arrondis du résultat. Néanmoins, il faut préciser que seules les unités de calcul à faible performance ont besoin de déterminer le nombre de zéros les plus à gauche.
On peut calculer ce nombre de zéros à gauche simplement à partir de l'indice du premier 1. On a vu plus haut comment trouver l'indice de ce 1 le plus à gauche. Le nombre de 0 à gauche est simplement égal au nombre de bits de notre nombre, auquel on soustrait la position de ce 1.
Pour un nombre de N bits, le nombre de ces zéros à gauche peut varier entre 0 et N. Si on a 0 zéros non-significatif, dans ce cas, le bit de plus à gauche est un 1. Si jamais on a N de ces zéros, c'est que tous les bits du nombre sont à zéro.
Find first zero byte
Maintenant, nous allons voir comment repérer le premier byte à zéro d'un registre ou d'un entier. On essaiera également de déterminer sa position relative dans ce byte.
Cet algorithme est exploité dans les bibliothèques standards de certains langages, comme le C. En effet, les chaînes de caractère du C suivent un modèle de stockage qui consiste à les conserver sous la forme d'un tableau de bytes, chaque byte encodant un caractère. La longueur de cette structure n'est pas gardée en mémoire ; à la place, on ajoute un caractère spécial, le caractère nul, à la fin de la chaîne. Celui-ci est représenté en binaire par un zéro.
Intuitivement, on pourrait croire que les fonctions qui manipulent ces chaînes de caractère, comme strlen ou strcpy, travaillent byte par byte. Mais, dans la réalité, ce serait un véritable gâchis en terme de performances. En effet, nos processeurs modernes sont reliés au cache (ou à la mémoire) par un bus de la même taille que les registres. Ainsi, notre cache nous permet de lire ou écrire par des paquets de 16, 32 ou 64 bits, suivant le processeur utilisé. Pour mieux exploiter la bande passante du cache, la plupart des implémentations de ces fonctions lisent donc la chaîne paquet par paquet.
Mais, en utilisant cette technique, comment savoir si l'on a atteint la fin de chaîne ? Pas le choix : on doit regarder si un des bytes qui compose le paquet est à zéro. Une solution intuitive mais inefficace serait d'effectuer une série de comparaisons qui compare chaque byte avec zéro. Néanmoins, cette technique utilise plusieurs branchements, qui constituent un goulot d'étranglement sur nombre d'architectures actuelles. De plus, d'autres solutions plus rapides existent.
Pour faciliter l'explication de ces solutions, on va considérer des entiers codés sur 32 bits, ce qui fait 4 bytes. Dans ce qui va suivre, nous allons utiliser quatre variables booléennes b0, b1, b2 et b3, qui indiquent si le byte correspondant de l'entier est non nul.
Le résultat de notre algorithme sera un entier, qui s’interprète comme suit :
- s'il vaut zéro, alors le le byte associé à b0 est nul ;
- s'il vaut 1, alors le le byte associé à b1 est nul ;
- s'il vaut 2, alors le le byte associé à b2 est nul ;
- s'il vaut 3, alors le le byte associé à b3 est nul ;
- s'il vaut 4, tous les bytes du nombre sont non-nuls.
La solution naïve expliquée ci-dessus reviendrait à tester séquentiellement si :
- b0 vaut 0 (on retourne 0) ;
- b1 vaut 0 (on retourne 1) ;
- b2 vaut 0 (on retourne 2) ;
- b3 vaut 0 (on retourne 3) ;
- sinon, on retourne 4.
Afin d'éviter les branchements, on remarque d'ores et déjà que le résultat peut être calculé grâce aux valeurs de ces variables : il suffit de les additionner, en faisant un AND sur les valeurs précédentes :
b0 + (b0 . b1) + (b0 . b1 . b2) + (b0 . b1 . b2 . b3)
Il reste maintenant à savoir comment calculer les valeurs de bi efficacement.
Une manière de le faire est d'utiliser uniquement le bit de poids fort du byte, en remplaçant tous les bytes nuls par 0xxx xxxx et tous les bytes non nuls par 1xxx xxxx. Pour cela, il suffit simplement d'ajouter à chacun d'entre eux la valeur 0111 1111 (0x7F en hexadécimal). Ainsi, tous les bytes nuls deviendront 0111 1111, tandis que les bytes non-nuls deviendront de la forme 1xxx xxxx.
On a cependant un problème pour les entrées supérieures à 1000 0000 : l'addition déborde. Le résultat ne tient pas dans un byte. C'est le cas de 1111 1111 :
1111 1111 + 0111 1111 = 1 0111 1110
Pour éviter ces débordements, on peut faire un masque sur l'entier avant l'opération, en lui enlevant le premier bit. Si on note x l'entier ou le registre qui est considéré en entrée, alors la transformation peut se noter comme suit :
x2 = (x . 0x7F7F7F7F) + 0x7F7F7F7F
Cette technique du masque a toutefois un léger défaut : le byte 1000 000, quand on lui aura appliqué le masque, vaudra également 0000 0000, et son bit de poids fort ne sera pas à 1 à la fin de l'opération. Pour positionner ce bit sans perdre la généralité de l'opération, on peut effectuer un OR x (qu'on notera | pour le différencier de l'addition), puisque cette instruction ne positionnera pas de bits à 0 par rapport à l'original.
x2 = ((x . 0x7F7F7F7F) + 0x7F7F7F7F) | x
Il reste enfin à récupérer chaque bi. De simples décalages de bits nous permettront d'obtenir leurs valeurs :
b0 = (x2 >> 7) . 1
b1 = (x2 >> 15) . 1
b2 = (x2 >> 23) . 1
b3 = (x2 >> 31) . 1
Pour calculer la position du premier byte à zéro en minimisant le nombre d'instructions finales, on peut effectuer un AND directement dans l'instruction suivante :
b0 = (x2 >> 7) . 1
b1 = (x2 >> 15) . 1 . b0
b2 = (x2 >> 23) . 1 . b1
b3 = (x2 >> 31) . 1 . b2
En outre, comme x . 1 = x, on peut simplifier comme suit :
b0 = (x2 >> 7) . 1
b1 = (x2 >> 15) . b0
b2 = (x2 >> 23) . b1
b3 = (x2 >> 31) . b2
On obtient finalement (on note r le résultat) :
x2 = ((x . 0x7F7F7F7F) + 0x7F7F7F7F) | x
b0 = (x2 >> 7) . 1
b1 = (x2 >> 15) . b0
b2 = (x2 >> 23) . b1
b3 = (x2 >> 31) . b2
r = b0 + b1 + b2 + b3
Arithmétique et Branch free code
Les opérations bit à bit permettent aussi d'effectuer certains calculs arithmétiques assez simplement. D'ordinaire, de nombreuses opérations, comme trouver le maximum de deux entiers, la valeur absolue, etc; ne sont pas implémentées naïvement avec des conditions et des branchements. Sur les processeurs modernes, les branchements sont en effet des opérations couteuses, qu'il vaut mieux éviter. Dans ces conditions, effectuer des calculs arithmétiques avec des opérations bit à bit est un bon investissement.
Dans ce qui va suivre, nous allons évidemment travailler avec des nombres en complément à deux.
Valeur absolue
Prenons un premier exemple : la valeur absolue. Celle-ci peut se calculer de trois manières différentes. Cependant, toutes ces méthodes nécessite d'isoler le bit de signe. Pour cela, il suffit d'utiliser un décalage logique pour déplacer ce bit et le mettre dans le bit de poids faible. Dans ce qui suit, ce bit de signe sera noté $y$.
La valeur absolue d'un nombre $x$ peut se calculer comme ceci :
- $( x \oplus y) - y$
- $( x + y) \oplus y$
- $x - ((2 \times x) . y)$
Pour obtenir l'inverse de la valeur absolue, il suffit de prendre l'opposée de celle-ci. En appliquant un simple - devant les expressions du dessus, on peut alors avoir diverses formules pour le calcul de l'inverse de la valeur absolue :
- $ y - ( x \oplus y) $
- $ ( y - x ) \oplus y $
- $ ((2 \times x) . y) - x $
Moyenne
Calculer la moyenne de deux nombres peut sembler simple comme bonjour. Il suffit d'appliquer la formule (x + y) / 2. Mais cette expression peut donner lieu à un débordement d'entier : le calcul de x + y peut dépasser la taille d'un registre, ce qui donnera un résultat totalement faux. Pour éviter cela, on peut ruser en utilisant des opérations bit à bit.
Je ne sais pas si vous avez déjà construit un additionneur entier, mais ce que l'on va voir est basé sur un principe assez proche. Pour calculer la somme de deux bits, un additionneur va calculer deux choses : le bit de la somme, et la retenue. La somme de deux bits a et b vaut onc :
$a \oplus b$
Tandis que la retenue vaut :
$a . b$
Maintenant, prenons deux nombres. On peut calculer la somme de ces deux nombres A et B sans tenir compte des retenues. Le résultat sera :
$A \oplus B$
Si on calcule ensuite uniquement les retenues, le résultat sera :
$(A . B) << 1$
Le décalage vient du fait que les retenues sont à prendre en compte la colonne suivante, quand on effectue d'addition en colonne.
Dans ces conditions, on peut en déduire que :
$ A + B = (A \oplus B) + ( (A . B) << 1)$
Maintenant, divisons le tout par deux. Cela revient à tout décaler d'un cran vers la droite. On obtient :
$ ( A + B ) / 2 = (A \oplus B) >> 1 + (A . B)$
On remarque que le terme de gauche de notre équation n'est autre que la moyenne. On sait donc maintenant comment calculer la moyenne de deux nombres sans overflow. Il suffit juste de calculer :
$(A \oplus B) >> 1 + (A . B)$
Il va de soit qu'en matériel, cette astuce est inutile : il suffit de garder le bit d'overflow de l'additionneur et le prendre en compte dans le décalage, pour garder un résultat correct.
Multiplication par une constante
Les opérations de multiplication entière ne sont pas franchement les plus gourmandes en temps d’exécution. Ceci dit, toute optimisation est bonne à prendre. Les compilateurs modernes sont capables d'optimiser un grand nombre de multiplications pour les replacer par des opérations plus rapides. Cela arrive souvent lorsqu'on utilise des tableaux : les calculs d'adresses localisés dans des boucles peuvent parfois être optimisés et certaines multiplications sont alors remplacées par des additions. De quoi gagner quelques cycles.
Une autre opportunité d'optimisation : la multiplication par une constante. Il est parfois possible de remplacer une multiplication par une constante par une suite d'instructions plus rapide. Au niveau matériel, la même chose est possible : il est possible de simplifier la conception d'un multiplieur, si celui-ci doit multiplier par une constante.
Par une puissance de 2
Dans certaines situations, un décalage vers la gauche de $n$ rangs est équivalent à une multiplication par $2^n$. Attention toutefois : cela ne marche que pour des entiers non-signés ou pour des entiers signés positifs. Pour les entiers négatifs, c'est une autre paire de manches.
En conséquence, les compilateur ne remplacent des multiplications par $2^n$ que lorsqu'ils savent que l'entier à multiplier est un entier non-signé, ou lorsqu'ils arrivent à prouver que l'entier en question est toujours positif au moment d'effectuer la multiplication. Dans le cas contraire, cette optimisation n'est jamais effectuée, par sécurité.
Shift and add
Mais comment gérer les multiplication par une constante qui n'est pas une puissance de deux ? Aussi bizarre que cela puisse paraitre, il y a deux méthodes. Suivant la situation, l'une d'entre elle sera plus rapide que l'autre. Tout dépend du nombre de bits à 1 dans la constante. Commençons par la première méthode.
Comme vous le savez, tout nombre entier est une somme de multiple de puissance de deux. C'est d'ailleurs le principe qui est derrière le binaire. Dans ce cas, multiplier par une puissance, c'est multiplier par une somme de puissance de deux. Avec quelques manipulations algébriques simple, cette multiplication peut se transformer en une somme de multiplication par une puissance de deux.
Supposons que je veuille effectuer une multiplication entre un nombre A, et une constante B.
$A \times B$
Il est évident que B est une somme de puissances de deux. Dans ce cas, je peux remplacer B par la somme de puissance de deux qui correspond.
Dans ce qui va suivre, nous allons prendre B = 5. Pour rappel, 5 = 4+1, ce qui fait que $5 = 2^2 + 2^0$
$A \times ( 2^2 + 2^0 )$
Comme on le sait tous, la multiplication est distributive. C'est à dire que $ a \times (b + c) = (a \times b) + (a \times c)$. J'utilise cette propriété sur l'équation du dessus, et je trouve :
$( A \times 2^2 ) + ( A \times 2^0 )$
Dans cette expression, on a donc une somme, qui additionne quelques termes. Ces termes sont tous des multiplications par une puissance de deux. On peut les remplacer par un décalage vers la gauche.
$( A << 2 ) + ( A << 0 )$
Ce qui donne :
$( A << 2 ) + A $
Ainsi, la multiplication par 5 peut se remplacer en un décalage à gauche de 2 rangs, et une addition.
Le principe reste le même pour toute multiplication par une constante : en décomposant la constante en puissance de deux, et avec quelques calculs, on peut transformer une multiplication par une constante en série de décalages et d'additions.
Le nombre de décalages effectué est égal au nombre de bits à 1 dans la constante (sa population count). Le nombre d'addition est presque identique. Si la constante contient donc trop de bits à 1, il se peut que le nombre de décalage et d'addition soit trop important : une multiplication peut être plus rapide. Cette technique ne marche donc que pour les nombres ayant une population count faible : 2-3 bits, parfois plus sur les architectures ayant une multiplication particulièrement lente. Mais pas plus.
Shift and substract
Dans le cas où un nombre contient beaucoup de bits à 1, il existe une seconde méthode. Elle se base sur un principe légèrement différent, mais assez similaire à celui utilisé dans la méthode précédente.
Comme vous le savez, un nombre entier peut s'écrire sous la forme d'une somme de puissance de deux. Par exemple, $5 = 2^2 + 2^0$.
Ceci dit, 5 peut aussi s'écrire sous une autre forme. Si on remarque bien, $5 = 8 - 3$. Dans cette expression, 8 est une puissance de 2, et 3 est un nombre comme un autre. Si on réfléchit bien, tout nombre entier peut s'écrire sous la forme $2^n - x).
Reprenons notre exemple avec le 5.
$5 = 8 - 3$
Dans cette expression, on peut remplacer chaque nombre par son expression en binaire. En clair, on le remplace par la somme de puissances de deux qui correspond.
$5 = 2^3 - ( 2^1 + 2^0 )$
Cette expression peut se récrire en utilisant uniquement des soustractions, par quelques bidouilles algébriques.
$5 = 2^3 - 2^1 - 2^0$
Maintenant, supposons que l'on veuille multiplier un nombre A par 5.
$A \times 5$
On peut alors remplacer 5 par l'expression avec décalages et soustractions :
$A \times ( 2^3 - 2^1 - 2^0 )$
En se rappelant que la multiplication est distributive, on obtient :
$( A \times 2^3 ) - ( A \times 2^1 ) - ( A \times 2^0 )$
Dans cette expression, on peut alors remplacer les multiplication par des puissances de deux par des décalages à gauche :
$( A<< 3 ) - ( A << 1 ) - ( A << 0 )$
Comme on le voit, cette expression ne contient que des décalages et des soustractions.
Et le principe est le même pour tout entier. Il suffit d'écrire la constante comme une puissance de deux à laquelle on aurait soustrait ce qu'il faut. Pour cela, il suffit de prendre la puissance de deux immédiatement supérieure à notre constante : cela simplifie les calculs et diminue le nombre de soustractions.
Pour savoir combien de décalages et de soustractions on a besoin, il faut revenir à notre algorithme.
Supposons que notre constante vaille x. On peut encoder celle-ci sur $log(x)$ bits. Il faut savoir qu'avec N bits, on peut stocker tous les nombres de 0 à $2^n - 1$. La puissance de deux immédiatement supérieure prendra alors un bit de plus. La puissance de deux immédiatement supérieure va prendre exactement $log(x) + 1$ bits.
Ensuite, on soustrait alors un certain nombre pour obtenir cette constante. En clair :
constante + nombre à soustraire = puissance de deux choisie
Or, si on calcule sur n bits, la puissance de deux vaut zéro. En clair :
constante + nombre à soustraire = 0
Autrement dit :
constante = - nombre à soustraire
Le nombre à soustraire est donc le complément à deux de la constante, codé sur n bits.
Cela nous dit donc que plus un nombre à de bits à 1, plus son complément à deux aura de bits à 0 : le nombre de soustractions à effectuer sera donc plus faible. Cette technique marche donc nettement mieux pour les nombres remplis de 1.
Division par une constante
Après la multiplication par une constante, il faut savoir que la division par une constante peut aussi être améliorée.
Par une puissance de deux
Comme je l'ai dit plus haut, un décalage vers la droite de n rangs revient à diviser un nombre positif par $2^{n}$. Avec des nombres négatif, ce n'est pas le cas : le bit de signe rentre dans le nombre, et on obtient un résultat qui n'a pas grand sens mathématiquement.
Il faut remarquer un petit détail : lorsqu'on effectue un décalage à droite -, certains bits de notre nombre vont sortir du résultat et être perdus. Cela a une conséquence : le résultat est tronqué ou arrondi. Plus précisément, le résultat d'un décalage à droite de n rangs sera égal à la partie entière du résultat de la division par $2^{n}$.
Pour obtenir des décalages qui fonctionnent normalement avec des nombres négatifs, on a inventé les arithmetics shifts. Ils sont similaires aux logical shift, à un détail prêt : pour les décalages à droite, le bit de signe de notre nombre n'est pas modifié, et on remplit les vides laissés par le décalage avec le bit de signe.

Ces instructions sont équivalentes à une multiplication/division par $2^n$, que le nombre soit signé ou non, à un détail prêt : l'arrondi n'est pas fait de la même façon pour les nombres positifs et négatifs. Pour donner un exemple, $ \frac {9} {2}$ sera arrondi en 4, tandis que $\frac {-9} {2}$ sera arrondi en -5.
Par une constante arbitraire
Pour ce qui est de la division par une constante arbitraire, il est possible d'utiliser une technique d'optimisation particulièrement efficace : la multiplication réciproque. Cette technique nous permet de remplacer la division par une constante en une multiplication.
Mais tout d'abord, nous devons préciser une chose. Lorsqu'on multiplie deux nombres de n bits, leur produit a une taille qui est de 2n bits. On a besoin de deux fois plus de bits pour le résultat. D'ordinaire, on s'en moque, et on se contente de garder les n bits de poids faible.
Dans ce qui va suivre, nous allons avoir besoin des n bits de poids fort. Pour cela, il faut que le processeur de la machine dispose d'instructions nous permettant de calculer ces bits de poids fort.
Certains processeurs disposent d'une instruction qui effectue la multiplication et ne conserve que les bits de poids forts dans un registre. Pour d'autre, l'instruction de multiplication conserve ces bits de poids fort et les bits de poids faible, en utilisant deux registres. Sur d'autres processeurs, l'instruction peut conserver les deux, ou seulement les bits de poids faible ou seulement les bits de poids fort : tout dépend du nombre de noms de registres et du mode d’adressage utilisé.
La multiplication réciproque est basée sur un principe simple : diviser par $N$, c'est multiplier par $\frac{1}{N}$. Si $N$ est une constante, alors on peut pré-calculer $\frac{1}{N}$ et éliminer ainsi la division. Quand on effectue ce genre de calculs sur des nombres flottants, il n'y a pas de problème, hormis une légère baisse de précision du résultat.
Mais pour les nombres entiers, ce genre de bidouille ne marche plus : la division entière de $\frac{1}{N}$ donnera forcément zéro. Aussi, la multiplication réciproque va tenter de trouver une constante telle que si on multiplie par celle-ci, et on récupère les n bits de poids fort, on aie le même résultat que si l'on avait divisé par N. Cette constante s'appelle la cconstante réciproque. Mais comment obtenir cette constante ?
le principe de base est que la constante réciproque doit valoir $\frac {2^{n}} {N}$, avec n le nombre de bits de N.
Pour comprendre pourquoi, regardons ce que donne la division d'un nombre A par la constante B :
On cherche :
$\frac{A}{B}$
Multiplions $A$ par la constante réciproque de B. Cette constante vaut : $\frac {2^{n}}{B}$.
$A \times \frac {2^{n}}{B}$
Se simplifie en :
$\frac {2^{n} \times A}{B}$
Ce qui donne :
$2^{n} \times \frac {A}{B}$
Vu que multiplier par $2^n$, c'est comme décaler à droite de n rangs, alors on a :
$\frac {A}{B} << n$
Le résultat de la multiplication est codé sur 2n bits. En comparaison, le résultat de la division, si elle avait été faite, aurait été codé sur n bits. Il est alors évident que le décalage par n signifie que le résultat sera placé dans les n bits de poids fort du résultat.
Dans les faits, les choses se compliquent pour certaines constantes. Il arrive parfois que $\frac {2^{n}} {N}$ ne tombe pas juste. C'est notamment le cas pour N = 10, 7, 11, et grosso-modo, tout ce qui n'est pas une puissance de deux. Dans ce cas, il arrive que l'imprécision de la constante réciproque soit à l'origine d'erreurs de calcul : sur certains dividendes, le résultat doit être corrigé avant d'être utilisable. Cette correction est une simple addition, qui ajoute un paramètre déterminé, fixe, qui dépend de la constante.
Dans ce cas, le mieux est de rechercher des constantes proches de la constante réciproque qui donnent de meilleurs résultats. Si vous voulez, un site web permet de calculer des constantes réciproques pour certaines valeurs. Le voici : http://www.hackersdelight.org/magic.htm
Voici les constantes réciproques pour les 20 premiers nombres :
| Constante | Constante réciproque |
|---|---|
| 3 | 2863311531 |
| 5 | 3435973837 |
| 7 | 3067833783 |
| 9 | 954437177 |
| 11 | 3123612579 |
| 13 | 3303820997 |
| 15 | 4008636143 |
| 17 | 4042322161 |
| 19 | 678152731 |
Modulo par une constante
Après avoir vu la multiplication et la division, nous pouvons maintenant passer au modulo par une constante. Pour ce qui est de calculer le modulo par une constante qui n'est pas une puissance de deux, il n'y a pas malheureusement pas grand chose à faire. Nous allons donc seulement regarder à quoi ressemble le modulo par une puissance de 2.
Dans le cas d'un nombre positif, une simple opération AND bit à bit suffit. Pour comprendre pourquoi, nous allons reprendre, encore une fois, l'écriture en binaire d'un nombre. Celuic-i est écrit sous la forme d'une somme de puissances de deux.
$2^n + 2^{n-1} + 2^{n-2} + ... + 2^{x+1} + 2^x + 2^{x-1} +... + 2^2 + 2^1 + 2^0$
Par définition, le modulo d'un nombre va prendre le reste de la division par un entier. Si calcule le reste modulo $2^x$, cela veut dire qu'on doit supprimer tous les multiples de $2^x$ dans l'écriture binaire de notre nombre. Cela se fait en mettant les bits associés à ces puissances à zéro.
En clair : pour obtenir le modulo, on doit mettre à zéro les n bits les plus à droite dans l'écriture binaire de notre nombre. Cette mise à zéro se fait en utilisant une opération AND, avec la constante qui va bien. La constante qui va bien fait très exactement $2^n - 1$.
Pour ce qui est des nombres négatifs, le coup du AND ne marche pas. Mais on peut toujours prendre la valeur absolue de notre nombre, calculer le modulo avec un AND, et prendre l'opposé, cela marche tout aussi bien.
Racine carrée inverse flottante
Maintenant, nous allons voir une bidouille vraiment virile. Il s'agit d'un algorithme de calcul incorporé dans certains moteurs de jeux vidéo. On ne sait pas qui l'a inventé, mais il est devenu célèbre lors de la publication du code source de Quake 3 arena, un vieux fast FPS comme on en fait plus, très sympa à jouer en LAN. Un vrai jeu, quoi !
Bref, dans les jeux vidéo, on a souvent besoin de calculer $\frac{1}{\sqrt{x}}$. Ce calcul est évidemment effectué sur des nombres flottants. Mais à l'époque de la création de ce jeu vidéo, les opérations flottante étaient très lentes. Et elles le sont toujours un petit peu, d'ailleurs. Pour diminuer la lenteur du calcul de $\frac{1}{\sqrt{x}}$, on a inventé la Fast Inverse SQRT, afin de calculer celle-ci en utilisant uniquement des opérations entières !
Cet algorithme prend un flottant 32 bits, et donne une approximation de $\frac{1}{\sqrt{x}}$.
Cet algorithme est très simple, jugez plutôt :
$0x5f3759df - ( nombre >> 1 )$
Champs de bits
Il arrive parfois que l'on aie besoin d’accéder à un bit particulier dans un nombre. Pour donner un exemple, on peut vouloir récupérer le bit de signe d'un nombre, pour ajuster certaines opérations. Par exemple, si vous voulez remplacer une division par 16 par un décalage, vous aurez besoin du bit de signe pour gérer le cas d'un dividende négatif.
Il arrive aussi que certains développeurs décident de compacter plusieurs données dans un seul entier. Par exemple, prenons le cas d'une date, exprimée sous la forme jour/mois/année. Un développeur normal stockera cette date dans trois entiers : un pour le jour, un pour le mois, et un pour la date. Mais un programmeur plus pointilleux sera capable d'utiliser un seul entier pour stocker le jour, le mois, et l'année. Pour cela, il raisonnera comme suit :
- un mois comporte maximum 31 jours : on doit donc encoder tous les nombres compris entre 1 et 31, ce qui peut se faire en 5 bits ;
- une année comporte 12 mois, ce qui tient dans 4 bits ;
- et enfin, en supposant que l'on doive gérer les années depuis la naissance de Jésus jusqu'à l'année 2047, 11 bits peuvent suffire.
Dans ces conditions, notre développeur décidera d'utiliser un entier de 32 bits pour le stockage des date :
- les 5 bits de poids forts serviront à stocker le jour ;
- les 4 bits suivant stockeront le mois ;
- et les bits qui restent stockeront l'année.
Seul problème : pour rendre cette date utilisable, notre développeur doit pouvoir sélectionner certaines suites de bits dans cet entier : le jour, le mois, l'année, etc. Comment fait-il ? C'est ce que cette sous-partie va vous expliquer.
Modifier un bit
Dans ce qui va suivre, nous allons voir comment modifier un bit dans un nombre, sans toucher aux autres. Cela a peu d'utilité, mais il est important de comprendre le principe. A quoi cela peut-il servir ? Et bien le développeur qui veut modifier une date alors qu'il a ragroupé les jours/mois et année dans un seul entier.
Autre exemple, supposons que j'ai regroupé dans un nombre tout un tas de bits, dont chacun a une signification bien précise. Par exemple, je peux regrouper les droits d'accès dans un fichier dans un nombre : un des bits du nombre me dira alors si je peux écrire dans le fichier, un autre me dira si je peux le lire, un autre si… Bref, si jamais je veux modifier mes droits en écriture de mon fichier, je dois mettre un bit bien précis à 1 ou à 0 (suivant la situation).
Comment faire ? En utilisant des opérations bit à bit. Suivant ce que l'on veut faire, l'instruction utilisée sera différente, mais le principe reste le même. Il suffit d'effectuer une instruction bit à bit entre notre nombre, et une constante bien précise.
Set
Tout d'abord, nous allons voir comment mettre à 1 un bit dans un nombre. Pour cela, rien de plus simple : nous allons devoir trouver quelle opération bit à bit convient.
Prenons l'instruction OR. Celle-ci prend deux bits : un appartenant à notre nombre, et un autre appartenant à notre constante.
| Nombre | Constante | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Supposons que le bit de ma constante soit un zéro. Dans ce cas, on remarque que le résultat du OR est égal au bit du nombre à modifier. En clair :
$A + 0 = A$
| Nombre | Constante | OR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Par contre, si le bit de ma constante est un 1, le résultat du OR est égal à 1. En clair :
$A + 1 = 1$
| Nombre | Constante | OR |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Dans ces conditions, je sais que je peux mettre un bit à 1 en effectuant un OR entre ce bit, et une constante dont le bit de même poids est un 1. Pour laisser les autres bits inchangés, il me suffit de mettre les autres bits de ma constante à zéro.
Par exemple, prenons le nombre suivant :
$0110 1100 0001$
Je veux modifier le 4éme bit en partant de la droite. Pour cela, je dois utiliser une constante dont le 4éme bit en partant de la droite est un , et le reste des bits est à zéro. La constante est donc :
$0000 0000 1000$
On peut vérifier le calcul nous-même :
$0110 1100 0001 + 0000 0000 1000 = 0110 1100 1001$
Reset
Maintenant, regardons l'opération symétrique : mettre un bit à zéro. L'opération à utiliser est un AND. Celle-ci prend deux bits : un appartenant à notre nombre, et un autre appartenant à notre constante.
| Nombre | Constante | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Supposons que le bit de ma constante soit un 1. Dans ce cas, on remarque que le résultat du AND est égal au bit du nombre à modifier. En clair :
$A . 1 = A$
| Nombre | Constante | AND |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Par contre, si le bit de ma constante est un 1, le résultat du OR est égal à 1. En clair :
$A . 0 = 0$
| Nombre | Constante | AND |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
Dans ces conditions, je sais que je peux mettre un bit à 0 en effectuant un AND entre ce bit, et une constante dont le bit de même poids est un 0. Pour laisser les autres bits inchangés, il me suffit de mettre les autres bits de ma constante à 1.
Par exemple, prenons le nombre suivant :
$1111 0000 1111$
Je veux modifier le 4éme bit en partant de la droite. Pour cela, je dois utiliser une constante dont le 4éme bit en partant de la droite est un 0 , et le reste des bits est à 1. La constante est donc :
$1111 1111 0111$
On peut vérifier le calcul nous-même :
$1111 0000 1111 . 1111 1111 0111 = 1111 0000 0111$
Inversion
Pour inverser un bit, on doit utiliser un XOR. Et oui, reprenez la table du XOR :
| Nombre | Constante | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Regardons ce que si passe pour un bit de constante qui vaut 1 :
| Nombre | Constante | XOR |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 | 0 |
On remarque que $ A \oplus 1 = \overline{A}$
Par contre, $ A \oplus 0 = A$
| Nombre | Constante | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Pour inverser un bit d'un nombre, il faut effectuer un XOR entre ce bit, et une constante dont le bit de même poids est un 1. Pour laisser les autres bits inchangés, il me suffit de mettre les autres bits de ma constante à 0.
Par exemple, prenons le nombre suivant :
$1111 0000 1111$
Je veux inverser le 4éme bit en partant de la droite. Pour cela, je dois utiliser une constante dont le 4éme bit en partant de la droite est un 0 , et le reste des bits est à 1. La constante est donc :
$0000 0000 1000$
On peut vérifier le calcul nous-même :
$1111 0000 1111 \oplus 0000 0000 1000 = 1111 0000 0111$
Sélection
Reprenons l'exemple du développeur qui a stocké une date dans un seul entier. Supposons qu'il veuille récupérer le jour stocké dans cette date. Comment doit-il s'y prendre ? Nous allons d'abord voir le cas le plus simple : on veut récupérer un seul bit dans un nombre. Cela correspond à l'exemple du bit de signe. Puis nous allons voir comment récupérer un groupe de bit : cela correspond à l'exemple des dates donnée à l'instant.
Pour récupérer un bit, rien de plus simple. Il suffit de mettre tous les autres bits du nombre à zéro, et de décaler le tout pour placer le résultat sur le bit de poids faible. Le même principe peut être utilisé pour récupérer des groupes de bits entiers. Il suffit juste de choisir le bon décalage, et la bonne constante.
Par exemple, si je veux récupérer le 5 éme bit en partant de la droite dans le nombre 1111 0011. Il me suffit de mettre tous les bits à zéro, sauf le bit voulu. Pour cela, je dois effectuer un AND entre 1111 0011 et la constante 0001 0000. J'obtiens alors 0001 0000. Ensuite, un décalage logique de 4 rangs vers la droite me donnera le bit voulu : 0000 0001.
Toutefois, cette méthode a un défaut : les constantes utilisées sont souvent très longues, ce qui empêche d'utiliser le mode d'adressage immédiat pour celles-ci. Raccourcir ces constantes permet de gagner pas mal de place. On peut ruser un petit peu en effectuant le décalage avant la mise à zéro.
Exemple : je décale mon nombre 1111 0011 de 4 rangs vers la droite. J'obtiens 0000 1111. Ensuite, je mets tous les bits à zéro, sauf le bit de poids faible. La constante à utiliser est alors 0000 0001.
Dans cette situation, on remarque que la constante à utiliser est très courte : c'est 1. Cette constante est très courte, ce qui permet d'utiliser le mode d'adressage immédiat pour l'instruction AND. De quoi gagner quelques cycles.
Bit de parité
Les données d'un ordinateur ne sont pas des plus sûres qui soit. Évidemment, ces données peuvent être corrompues par un tiers malveillant, contenir des virus, etc. Mais certaines données sont corrompues pour des raisons qui ne relèvent pas de la volonté de nuire.
Par exemple, les transmissions de données via un réseau local ou internet peuvent subir des perturbations électromagnétiques entre leur envoi et leur réception. Évidemment, les câbles réseaux sont conçus pour limiter les erreurs, mais ils ne sont pas une protection magique, capable de supprimer les erreurs de transmission.
Dans le même genre, les mémoires ne sont pas des dispositifs parfaits, capables de fonctionner sans erreur. Pour donner un exemple, on peut citer l'incident de Schaerbeek. Le 18 mai 2003, dans la petite ville belge de Schaerbeek, une défaillance temporaire d'une mémoire faussa les résultats d'une élection. Cette ville utilisait une machine à voter électronique, qui contenait donc forcément une mémoire. Et on constata un écart de 4096 voix en faveur d'un candidat entre le dépouillement traditionnel et le dépouillement électronique. Mais ce n'était pas une fraude : le coupable était un rayon cosmique, qui avait modifié l'état d'un bit de la mémoire de la machine à voter.
Cet incident n'était pas trop grave : après tout, il a pu corriger l'erreur. Mais imaginez la même défaillance dans un système de pilotage en haute altitude…
Mais qu'on se rassure : il existe des techniques pour détecter et corriger les erreurs de transmission, ou les modifications non-prévues de données. Pour cela, divers codes de détection et de correction d'erreur ont vu le jour. Cet article vous parlera du code le plus simple qui soit : le bit de parité/imparité.
Celui-ci est présent dans un grand nombre de circuits électroniques, comme certaines mémoires RAM, ou certains bus (RS232, notamment) : sa simplicité est clairement un atout. Vu l'importance de son utilisation, il mérite bien un article.
Bit de parité horizontal mono-dimensionnel
Le bit de parité est une technique qui permet de détecter des erreurs de transmission ou d’éventuelles corruptions de données qui modifient un nombre impair de bits. Si un, trois, cinq, ou un nombre impair de bits voient leur valeur s'inverser (un 1 devient un 0, ou inversement), l'utilisation d'un bit de parité permettra de détecter cette erreur. Mais si un nombre pair de bit est modifié, il sera impossible de détecter l'erreur.
Dans tous les cas, il sera impossible de corriger l'erreur : le bit de parité ne permet que de détecter une erreur dans un ensemble de données, mais ne peut pas permettre de localiser le bit qui a subi une erreur de transmission/stockage.
Principe
Le principe caché derrière un bit de parité est simple : il suffit d'ajouter un bit supplémentaire aux bits à stocker. Ce bit en plus s'appelle le bit de parité.
Ce bit, le bit de parité vaudra :
- zéro si le nombre de bits à 1 dans le nombre à stocker (bit de parité exclu) est pair ;
- 1 si ce nombre est impair.
Le but d'un bit de parité est de faire en sorte que le nombre de bits à 1 dans le nombre à stocker, bit de parité inclus, soit toujours un nombre pair.
Prenons un exemple, avec le nombre 0000 0101. Celui-ci contient 6 bits à 0 et 2 bits à 1. La somme de tous ces bits vaut donc 2. Le bit de parité vaudra donc zéro. En plaçant le bit de parité au début du nombre, on obtient : 0 0000 0101.
Autre exemple : le nombre 1110 0101. Celui-ci contient 3 bits à 0 et 5 bits à 1. On trouve 5 bits à 1 dans ce nombre, ce qui donne un nombre impair. Le bit de parité vaudra donc un. Le total sera donc : 1 1110 0101.
En modifiant un bit, la parité du nombre total de bits à 1 changera : le nombre de bits à 1 sera diminué (si un 1 devient un 0) ou augmenté de 1 (cas inverse) et deviendra un nombre impair. Et ce qui est valable pour un bit l'est aussi pour 3, 5, 7, et pour tout nombre impair de bits modifiés. Par contre, si un nombre pair de bit est modifié, la parité du total ne changera pas et restera compatible avec la valeur du bit de parité : on ne pourra pas détecter l'erreur.
Détecter une erreur est simple : vérifie que le bit de parité du mot binaire envoyé est égal au bit de parité calculé à la réception. On peut aussi compter le nombre de bits à 1 dans le nombre à stocker, bit de parité inclus, et regarder si ce nombre est pair : s'il est impair, on sait qu'au moins un bit à été modifié.
Le XOR
Si je vous donne un ensemble de donnée de taille fixe, comment en calculer le bit de parité ?
Pour commencer, la majorité des algorithmes de calcul efficaces du bit de parité utilisent une opération bit à bit que l'on appelle le XOR.
Bit de parité de deux bits
En quoi ce XOR nous intéresse ? Très simple : il permet de calculer le bit de parité d'un nombre assez simplement, grâce aux propriétés du bit de parité.
Déjà, ce XOR nous permet de calculer facilement le bit de parité d'un mot binaire (d'un nombre). Pour faire simple, nous allons commencer par un cas simple : le calcul de parité d'un mot binaire de deux bits. Si vous faites le calcul, vous allez tomber sur ceci :
| A | B | Bit de parité |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ce qui est exactement le fonctionnement d'une porte XOR.
Algorithme itératif naïf
Maintenant, prenons le bit de parité d'un mot de trois bits : ce mot est composé d'un mot binaire de 2 bits, auquel on aurait ajouté un bit. Or, le bit de parité du mot de 3 bits est égal à un XOR entre le bit ajouté et le bit de parité du mot interne de 2 bits.
Pour donner quelques exemples :
- la parité de 110 est égale à la parité de $1 \oplus 10$ ;
- la parité de 010 est égale à la parité de $0 \oplus 10$ ;
- la parité de 100 est égale à la parité de $0 \oplus 10$ ;
- la parité de 001 est égale à la parité de $1 \oplus 00$ ;
- etc.
Ainsi, pour un mot de trois bits, notés $a_2$, $a_1$, $a_0$, le bit de parité vaut : $a_2 \oplus a_1 \oplus a_0$.
Et on peut généraliser pour le passage de 3 à 4 bits, ou celui de 4 à 5, etc. Quand on concatène un bit à un mot binaire, la parité du résultat est égale à la parité du mot XOR le bit ajouté.
Dit autrement : bit-parité ( bit concat mot ) = bit $\oplus$ bit-parité ( mot ).
L'explication est simple :
- quand on ajoute un 0, le nombre de bits à 1 reste inchangé : le bit de parité reste identique ;
- quand on ajoute un 1, le nombre de bits à 1 augmente de 1 et passe donc de pair à impair ou d'impair à pair : le bit de parité est inversé.
On peut illustrer le tout avec le tableau suivant :
| Nombre de bits à 1 dans le Mot binaire | Bit | Résultat |
|---|---|---|
| Pair | 0 | Pair |
| Pair | 1 | Impair |
| Impair | 0 | Impair |
| Impair | 1 | Pair |
Si on remplace Pair et Impair par la valeur du bit de parité correspondant, on obtient ceci :
| Bit de parité du mot | Bit ajouté | Bit de parité final |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ce qui correspond bien à un XOR entre le bit ajouté t le mot initial.
Il suffit donc d'appliquer le XOR un nombre suffisant de fois pour calculer le bit de parité d'un nombre.
Ainsi, pour un mot de n bits, notés $a_n$, $a_{n-1}$, … , $a_1$, $a_0$, le bit de parité vaut : $a_n \oplus a_{n-1} \oplus ... \oplus a_1 \oplus a_0$.
L’algorithme de calcul du nombre de parité est alors assez évident. Pour ceux qui sont familiers avec le C et avec ses opérateurs bit à bit, voici une implémentation naïve de ce bit de parité :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | unsigned parity_bit (unsigned word ,unsigned size) { unsigned parity_bit = 0 ; // on itère sur chaque bit du mot à traiter for(unsigned index = 0 ; index < size ; ++index) { //sélection du bit de poids faible unsigned temp = word & 1 word = word >> 1 ; // XOR entre le bit sélectionné et le bit de parité des bits précédents. parity_bit = parity_bit ^ temp ; } return parity_bit ; } |
Cette solution a un temps de calcul qui est linéaire en le nombre de bits de la donnée dont on veut calculer le bit de parité. On peut faire mieux en utilisant d'autres propriétés du bit de parité.
Algorithme itératif optimisé
On peut améliorer l'algorithme du dessus en utilisant la propriété suivante : si on concatène deux mots binaire, alors le bit de parité du mot obtenu est égal au XOR des bits de parité des deux mots concaténés.
Dit autrement : bit-parite ( mot_A concat mot_B ) = bit-parite ( mot_A ) $\oplus$ bit-parite ( mot_B ).
Pour donner quelques exemples :
- le bit de parité de 10101010 est égal au bit de parité de 1010 $\oplus$ le bit de parité de 1010 ;
- le bit de parité de 11110000 est égal au bit de parité de 1111 $\oplus$ le bit de parité de 0000;
- le bit de parité de 11101000 est égal au bit de parité de 1110 $\oplus$ le bit de parité de 1000;
- le bit de parité de 10000001 est égal au bit de parité de 1000 $\oplus$ le bit de parité de 0001;
- etc.
Cette propriété peut s'expliquer assez simplement. Pour cela, il suffit de regarder le nombre de bits à 1 dans chaque mot à concaténer.
| Nombre de bits à 1 dans le mot binaire de gauche | Nombre de bits à 1 dans le mot binaire de droite | Nombre de bits à 1 dans le résultat |
|---|---|---|
| Pair | Pair | Pair |
| Pair | Impair | Impair |
| Impair | Pair | Impair |
| Impair | Impair | Pair |
Si on remplace Pair et Impair par la valeur du bit de parité correspondant, on obtient ceci :
| Bit de parité du mot | Bit ajouté | Bit de parité final |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ce qui est exactement le fonctionnement d'une porte XOR : CQFD.
Grâce à cette propriété du bit de parité, on peut travailler non sur des bits, mais aussi sur des octets. Prenons un mot de 16 bits, par exemple : il me suffit de faire un XOR entre les bits de parité de ces deux octets. Or, la parité d'un octet peut se pré-calculer et être stockée dans un tableau une fois pour toute, afin d'éviter de nombreux calculs. Ainsi, l'algorithme vu précédemment peut être amélioré pour traiter non pas un bit à la fois, mais plusieurs bits à la fois.
On peut aussi inventer un autre algorithme du calcul du bit de parité, assez inefficace, basé sur une fonction récursive. Le principe est de couper le mot dont on veut la parité en deux morceaux. On calcule alors la parité de ces deux morceau, et on fait un XOR entre ces deux parités. Le code obtenu est alors celui-ci :
1 2 3 4 5 6 7 8 9 10 11 12 13 | unsigned parity (unsigned word, size) { if (word <= 1) { return word ; } else { unsigned gauche = word >> (size/2) ; unsigned droite = word % (size/2) ; return parity(gauche, size/2) ^ parity (droite, size/2)) ; } } |
Mais on peut faire nettement mieux…
Population count
Il faut savoir que le bit de parité entretient des relations conceptuelles assez intéressantes avec certaines opérations bit à bit. Il a notamment un lien avec la population count. Pour rappel, la population count d'un nombre est le nombre de ses bits qui sont à 1. Par définition, le bit de parité a pour but de faire en sorte que la population count d'une donnée soit toujours pair : la donnée à laquelle on ajoute le bit de parité sera pair, et aura toujours son bit de poids faible à zéro.
En conséquence, le bit de parité d'un nombre est égal au bit de poids faible de la population count d'un nombre. Et cette propriété permet de donner des algorithmes de calcul du bit de parité d'un nombre assez efficace.
Avec ce qu'on a dit auparavant, on peut en déduire un autre algorithme encore plus efficace. Certains algorithmes de population count ont une complexité logarithmique en le nombre de bits de la donnée d'entrée. Pour calculer un bit de parité avec une complexité logarithmique, il suffit donc de calculer la population count d'un nombre, et de prendre le bit de poids faible.
1 2 3 4 5 6 | unsigned population_count (unsigned word) ; unsigned parity_bit (unsigned word) { return population_count (word) & 1 ; } |
Cet algorithme est parfois utilisé sur des systèmes qui ont peu de mémoire, quand on a déjà programmé une fonction de population count : cela permet d'économiser un peu de mémoire programme. Mais cet algorithme n'est pas le plus efficace en terme de temps de calcul.
Algorithme en arbre
Il est possible de spécialiser l'algorithme de calcul de la Population Count, afin que celui-ci ne calcule que le bit de parité, et pas les autres bits de la Population Count. On obtient alors un algorithme relativement optimisé, assez difficile à comprendre. Pour illustrer l'algorithme, nous allons prendre l'exemple d'un nombre sur 8 bits. Nous allons noter N le nombre dont on recherche la population count.
Première étape : l'algorithme commence par grouper les bits du nombre par groupes de deux et les XOR. Pour cela, l'algorithme va avoir besoin de deux variables.
La première variable va stocker tous les bits à une position paire. Les autres bits sont mis à zéro. En clair :
variable1 = N . 01010101.
L'autre stockera les bits en position impaire, les autres sont mis à zéro. En clair :
variable2 = N . 10101010.
Puis, un petit décalage va mettre les bits des deux variables sur la même colonne.
variable2 >> 1
Enfin, on XOR ces deux variables.
variable 1 $\oplus$ variable 2.
Résumé de la première étape :
- variable1 = N . 01010101
- variable2 = (N . 10101010) >> 1
- variable 1 $\oplus$ variable 2.
Pour comprendre ce qui se passe, nous allons regarder de plus prêt ce qui se passe sur les bits de N. Supposons que notre nombre N aie 8 bits, notés comme ceci :
a7 a6 a5 a4 a3 a2 a1 a0
Variable2 $\oplus$ Variable1 donnera ceci :
| Variable | bit | bit | bit | bit | bit | bit | bit | bit |
|---|---|---|---|---|---|---|---|---|
| variable1 | 0 | a6 | 0 | a4 | 0 | a2 | 0 | a0 |
| variable 2 >> 1 | 0 | a7 | 0 | a5 | 0 | a3 | 0 | a1 |
| total | 0 | a6$\oplus$a7 | 0 | a4$\oplus$a5 | 0 | a2$\oplus$a3 | 0 | a0$\oplus$a1 |
La seconde étape est similaire, si ce n'est qu'elle isole les deux bits crées à l'étape précédente, et les XOR deux à deux.
- variable1 = N . 00010001
- variable2 = (N . 01000100) >>2
- variable 1 $\oplus$ variable 2.
| Variable | bit | bit | bit | bit | bit | bit | bit | bit |
|---|---|---|---|---|---|---|---|---|
| variable1 | 0 | 0 | 0 | a4$\oplus$a5 | 0 | 0 | 0 | a0$\oplus$a1 |
| variable 2 >> 1 | 0 | 0 | 0 | a6$\oplus$a7 | 0 | 0 | 0 | a2$\oplus$a3 |
| total | 0 | 0 | 0 | a4$\oplus$a5$\oplus$a6$\oplus$a7 | 0 | 0 | 0 | a0$\oplus$a1$\oplus$a2$\oplus$a3 |
Et on, poursuit ainsi de suite, jusqu'à obtenir le bit de parité de notre nombre. Dans notre exemple, une troisième étape suffit pour obtenir le résultat.
Troisième étape :
- variable1 = N . 00000001
- variable2 = (N . 00010000) >> 4
- variable 1 $\oplus$ variable 2.
| Variable | bit | bit | bit | bit | bit | bit | bit | bit |
|---|---|---|---|---|---|---|---|---|
| variable1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | a0$\oplus$a1$\oplus$a2$\oplus$a3 |
| variable 2 >> 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | a4$\oplus$a5$\oplus$a6$\oplus$a7 |
| total | 0 | 0 | 0 | 0 | 0 | 0 | 0 | a0$\oplus$a1$\oplus$a2$\oplus$a3$\oplus$a4$\oplus$a5$\oplus$a6$\oplus$a7 |
Vous remarquerez que cet algorithme fait conceptuellement la même chose que l'algorithme récursif.
L'algorithme final
L'algorithme du dessus peut encore être amélioré. Dans l'étape du dessus, on perd beaucoup de temps pour sélectionner les bits à XOR entre eux avec des masques bit à bit (les ET logiques) : on peut se passer de ces masquages. Pour cela, il faut choisir intelligemment les bits à XOR entre eux.
L'astuce est de découper le mot binaire en deux, de placer les deux morceaux obtenus d'un en dessous de l'autre, et de faire le XOR. En faisant cela à chaque étape, on obtient le bit de parité voulu.
Par exemple, supposons que notre nombre N aie 8 bits, notés comme ceci :
a7 a6 a5 a4 a3 a2 a1 a0
Le premier morceau est composé des bits a3 a2 a1 a0, et l'autre morceau des bits a7 a6 a5 a4.
On a donc variable1 : N and 00001111 , et variable2 : N >> 4.
variable2 $\oplus$ variable1 donnera ceci :
| variable | bit | bit | bit | bit | bit | bit | bit | bit |
|---|---|---|---|---|---|---|---|---|
| variable1 | 0 | 0 | 0 | 0 | a3 | a2 | a1 | a0 |
| variable 2 | 0 | 0 | 0 | 0 | a7 | a6 | a5 | a4 |
| total | 0 | 0 | 0 | 0 | a3$\oplus$a7 | a2$\oplus$a6 | a1$\oplus$a5 | a0$\oplus$a4 |
On reproduit la même chose durant une seconde étape : on a donc variable1 = N and 00000011 , et variable2 = N >> 2.
variable2 $\oplus$ variable1 donnera ceci :
| variable | bit | bit | bit | bit | bit | bit | bit | bit |
|---|---|---|---|---|---|---|---|---|
| variable1 | 0 | 0 | 0 | 0 | 0 | 0 | a3$\oplus$a7 | a2$\oplus$a6 |
| variable 2 | 0 | 0 | 0 | 0 | 0 | 0 | a1$\oplus$a5 | a0$\oplus$a4 |
| total | 0 | 0 | 0 | 0 | 0 | 0 | a1$\oplus$a5$\oplus$a3$\oplus$a7 | a0$\oplus$a4$\oplus$a2$\oplus$a6 |
Et on reproduit la même chose durant une dernière étape : on a donc variable1 = N and 0000001 , et variable2 = N >> 1.
variable2 $\oplus$ variable1 donnera ceci :
| variable | bit | bit | bit | bit | bit | bit | bit | bit |
|---|---|---|---|---|---|---|---|---|
| variable1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | a0$\oplus$a4$\oplus$a2$\oplus$a6 |
| variable 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | a1$\oplus$a5$\oplus$a3$\oplus$a7 |
| total | 0 | 0 | 0 | 0 | 0 | 0 | 0 | a1$\oplus$a5$\oplus$a3$\oplus$a7$\oplus$a0$\oplus$a4$\oplus$a2$\oplus$a6 |
L'algorithme peut s’implémenter en C comme ceci :
1 2 3 4 5 6 7 8 9 10 11 12 13 | unsigned parity_bit (unsigned word ,unsigned size) { unsigned parity_bit = 0 ; for(unsigned size_chunk = size/2 ; size > 1 ; size = size / 2) { unsigned gauche = word >> (size_chunk) ; unsigned droite = word % (size_chunk) ; parity_bit = gauche ^ droite ; } return parity_bit ; } |
Bit d'imparité horizontal mono-dimensionnel
Certains systèmes utilisent non pas un bit de parité, mais un bit d'imparité, conçu de façon à ce que le nombre de bits à 1 dans le nombre, bit d'imparité inclus, soit un nombre impair. Sa valeur est l'exact inverse de celle d'un bit de parité obtenu pour le même nombre.
Par exemple, reprenons le nombre 0000 0101. Celui-ci contient 6 bits à 0 et 2 bits à 1. La somme de tous ces bits vaut donc 2. Le bit de parité vaudra donc 1. En plaçant le bit de parité au début du nombre, on obtient : 1 0000 0101.
Autre exemple : le nombre 1110 0101.Celui-ci contient 3 bits à 0 et 5 bits à 1. On trouve 5 bits à 1 dans ce nombre, ce qui donne un nombre impair. Le bit d'imparité vaudra donc 0. Le total sera donc : 0 1111 0101.
Si vous êtes observateur, vous remarquerez que le bit de parité est l'exact inverse du bit d'imparité : quand le premier vaut 1, le second vaut 0, et réciproquement.
Là encore, il est impossible de détecter une erreur qui modifie un nombre pair de bits. Cette méthode a le même pouvoir de détection que le bit de parité. Même chose pour ce qui est de corriger les erreurs : ce bit d'imparité ne permet pas de localiser le bit modifié, et ne permet donc pas de corriger celui-ci.
Mots et octets de parité
Si on peut calculer le bit de parité d'un mot, il est aussi possible de calculer des octets de parité pour un ensemble de Byte/mots machine.
Pour mieux faire comprendre ce que je veux dire, je vais prendre un exemple : nous allons encore supposer que nous disposons de 8 entiers de 8 bits chacun. L'ensemble de ces données donne un mot de 64 bits. Nous allons prendre la suite de bit qui suit, dans notre exemple :
1100001010001000010010101001000010001001100100010100000101100101
Nous allons disposer ces bits en lignes et en colonnes.
- 11000010
- 10001000
- 01001010
- 10010000
- 10001001
- 10010001
- 01000001
- 01100101
Maintenant, nous allons calculer le bit de parité de chaque colonne.
- 11000010
- 10001000
- 01001010
- 10010000
- 10001001
- 10010001
- 01000001
- 01100101
- 10101100
Le résultat obtenu sur la dernière ligne est un octet de parité.
C'est cette technique qui est utilisée sur les disques durs montés en RAID 3, 5 6, et autres. L'avantage de cette organisation est qu'elle permet de reconstituer un octet manquant. Ainsi, si un disque dur ne fonctionne plus, on peut quand même reconstituer les données du disque dur manquant.
Pour comprendre pourquoi, reprenons le tableau d'octets du dessus. Imaginons qu'un des octets disparait :
- 11000010
- 10001000
- 01001010
-
- 10001001
- 10010001
- 01000001
- 01100101
- 10101100
Retrouver la donnée est alors très facile : il suffit de calculer la parité des octets restants, et de faire un XOR avec l'octet de parité.
Mais pourquoi cela marche ?
Pour comprendre pourquoi, nous allons prendre un exemple.
Il suffit de savoir une chose simple : XORer une donnée avec elle-même donne toujours zéro. $A \oplus A = 0$.
Maintenant, regardons ce que vaut notre octet de parité. Dans ce qui va suivre, nous allons supposer que l’opérateur $\oplus$ est un opérateur bit à bit. On va aussi supposer que les octets de donnée sont numérotés de 0 à 7, et sont notés $O_i$.
L'octet de parité vaut donc : $O_0 \oplus O_1 \oplus O_2 \oplus O_3 \oplus O_4 \oplus O_5 \oplus O_6 \oplus O_7$;
Maintenant, calculons l'octet de parité des données restantes. Vu que l'octet $O_3$ a sauté, on obtient : $O_0 \oplus O_1 \oplus O_2 \oplus O_4 \oplus O_5 \oplus O_6 \oplus O_7$;
Faites un XOR entre les deux, et vous obtenez :
$O_0 \oplus O_1 \oplus O_2 \oplus O_4 \oplus O_5 \oplus O_6 \oplus O_7 \oplus O_0 \oplus O_1 \oplus O_2 \oplus O_3 \oplus O_4 \oplus O_5 \oplus O_6 \oplus O_7$.
Or, vu que $A \oplus A = 0$, on peut simplifier le tout, et on obtient : $O_3$.
Bit de parité/imparité bi-dimensionnel
Si bits de parité et d'imparité ne peuvent pas corriger les erreurs, on peut adapter ceux-ci de manière à résoudre ce problème : il suffit de coupler un octet de parité avec quelques bits de parité pour pouvoir corriger des erreurs.
Pour cela, nous allons encore supposer que nous disposons de 8 entiers de 8 bits chacun.L'ensemble de ces données donne un mot de 64 bits. Nous allons prendre la suite de bit qui suit, dans notre exemple :
1100001010001000010010101001000010001001100100010100000101100101
Nous allons disposer ces bits en lignes et en colonnes.
- 11000010
- 10001000
- 01001010
- 10010000
- 10001001
- 10010001
- 01000001
- 01100101
Maintenant, nous allons calculer le bit de parité de chaque ligne, et celui de chaque colonne (l'octet de parité).
- 110000101
- 100010000
- 010010101
- 100100000
- 100010011
- 100100011
- 010000010
- 011001010
- 10101100-
Détecter une erreur est relativement simple avec cette organisation : il suffit de regarder les bits de parité de chaque ligne, ainsi que le mot de parité. Si le mot de parité est différent de 0, ou qu'un seul des bit de parité d'une ligne vaut 1, alors il y a une erreur.
Avec cette organisation, il est possible de déterminer quel est le bit qui a subit une erreur. Évidemment, cela demande certaines conditions : un seul bit doit avoir été modifié, pas un de plus.
On va supposer que c'est le cas : un seul bit est modifié. Ce bit est situé à l'intersection d'une ligne et d'une colonne. Sa modification entraînera la modification de deux bits de parité :
- celui de la ligne ;
- celui de la colonne.
Deux bits seront alors fautifs lors de la vérification : le premier bit permettra de localiser la ligne fautive, et l'autre la colonne. Le bit erroné est situé à l'intersection.
Bit de parité/imparité multi-dimensionnel
La technique vue précédemment peut s'adapter non pas avec une disposition en lignes et colonnes, mais aussi avec des dimensions en plus. On peut ajouter une dimension en plus à la grille et disposer les bits des données dans un cube. On peut aussi aller plus loin, et disposer les bits dans un hyper-volume, avec un nombre arbitraire de dimensions.



 )
)

