Nous allons lister ici les principaux résultats et définitions qui nous servirons par la suite. Ceci devrait être connu du lecteur, ou du moins accessible.
Motivations
L'intérêt de faire de la topologie, dans ce contexte, est d'avoir des outils pour faire de l'analyse. Vous savez déjà certainement comment faire de l'analyse sur la droite réelle (continuité, dérivabilité, intégration), on aimerait étendre ces notions à des situations plus générales. En particulier, on va essayer d'avoir toutes ces notions sur la sphère $\mathbf{S}^2$ (a priori très éloignée de la droite réelle).
Ainsi, la topologie permet de généraliser très facilement la notion de continuité et dans les cas métriques (c'est-à-dire quand on a une notion de distance) la notion de convergence.
Pour ce qui est de l'intégration et de la dérivabilité (qui deviendra de la différentiabilité, ou holomorphie en termes complexes), il faudra se donner des outils supplémentaires de calcul différentiel.
Dans la première partie, on dégagera la notion de continuité et d'homéomorphisme. La partie suivante nous donnera les outils de calcul différentiel et les prochains chapitres les réutiliseront pour analyser plus finement la structure de notre sphère.
Topologie de $\mathbf{C}$
Avant de commencer à faire de l'analyse, on va se donner des outils de topologie, auparavant appelée analysis situs (sans grand hasard). Il va donc s'agir de munir $\newcommand{C}{\mathbf{C}}\C$ d'une « topologie », c'est-à-dire un ensemble de parties « ouvertes » de $\C$ que nous définirons par les « voisinages » de $\C$.
Il y a plusieurs façons équivalentes de définir une topologie, ici j'ai fait le choix des voisinages mais on peut définir une topologie par :
- Ses ouverts ;
- ses fermés ;
- ses voisinages.
Même si je vais rappeler quels sont ces ensembles pour $\mathbf{C}$, il ne s'agira pas d'un cours de topologie. Ainsi, s'il vous manque des notions, vous devriez essayer de les combler avant de vous attaquer à ce tutoriel. On ne justifiera pas non plus que la structure donnée est bien une topologie mais muni de la topologie qui sera présentée, $\C$ est un espace topologique.
Voisinage, ouvert, fermés de $\C$
Voisinages
Soit $a\in \C$. Un voisinage de $a$, $V_a$, est une partie de $\C$ telle que :
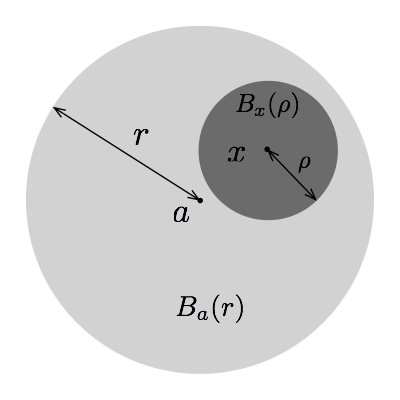
On appelle $B_a(r)$ la boule ouverte centrée en $a$ et de rayon $r$. Géométriquement, il s'agit du disque (sans sa frontière) centré en $a$ et de rayon $r$.
Sur l'image qui suit, un voisinage de $a\in \C$ a été représenté. La zone la plus foncée représente une boule ouverte centrée en $a$ contenue dans $V_a$ ce qui permet bien de qualifier ce dernier de voisinage de $a$.

Exemples
Deux exemples simples et importants à retenir :
- $B_a(r)$ est un voisinage de $a$ pour tout $r>0$ ;
- $\{a\}$ n'est pas un voisinage de $a$.
Ouverts
Une partie de $\C$ est dite ouverte si elle est voisinage de chacun de ses points. C'est-à-dire, $U\subset\C$ est un ouvert si, et seulement si,
Exemples
- $\mathbf{C}$ et $\emptyset$ sont deux ouverts ;
- $B_a(r)$ est un ouvert pour tous $a\in \C$ et $r>0$.
Fermés
Une partie de $\C$ est dite fermée si son complémentaire est une partie ouverte.
Il faut faire attention à ne pas croire qu'une partie ne peut pas être ouverte et fermée.
Exemples
- $\C$ et $\emptyset$ sont deux fermés ;
- Les boules fermés centrées en $a$ et de rayon $r$ définies par :
$$ \bar{B}_a(r) = \{z\in \C \, \lvert \, |z-a| \leq r\} $$
sont fermées.
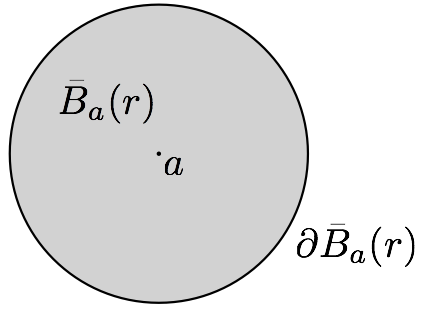
La notation $\partial \bar{B}_a(r)$ est explicitée dans ce qui suit.
Adhérence et intérieur
Soit $A\subset \C$. L'adhérence de $A$, notée $\bar{A}$, est le plus petit fermé contenant $A$. Son intérieur, noté $\overset{\circ}{A}$ est le plus grand ouvert contenu dans $A$.
Ainsi, on a les relations d'inclusions suivantes :
On définit la frontière de $A$ par la différence : $\partial A = \bar{A} -\overset{\circ}{A}$. Ainsi, une partie est fermée si elle contient tous les points de sa frontière et est ouverte si elle n'en contient aucun.
Convergence, continuité
Espace séparé et convergence
On dit qu'un espace topologique est séparé si deux points distincts admettent deux voisinages disjoints. C'est bien le cas pour $\C$ : étant donnés $x,y\in \C$ distincts et en prenant deux boules centrées en $x$ et $y$ et de rayons inférieurs à la moitié de la distance entre $x$ et $y$ on obtient deux voisinages disjoints de $x$ et $y$.
Considérons une suite $A = (a_n)_{n\in\mathbf{N}}$ de nombres complexes. On dit que la suite $A$ converge vers $a$ si pour tout voisinage, $V_a$, de $a$, il existe $n_0\in\mathbf{N}$ tel que :
Si on choisit des boules ouvertes comme voisinages de $a$, on retrouve la notion de convergence usuelle.
Comme $\C$ est un espace séparé, si $A$ converge vers $a$, alors elle converge uniquement vers $a$ et on note :
la limite de cette suite.
Continuité
Soit $f : \C\to \C$. On dit que $f$ est continue si pour tout $a\in \C$ et pour tout voisinage $V_{f(a)}$ de $f(a)$, $f^{-1}(V_{f(a)})$ (l'image réciproque de $V_{f(a)}$ par $f$) est un voisinage de $a$.
De même, en remplaçant les voisinages de $f(a)$ par des boules ouvertes centrées en $f(a)$, on retrouve la notion de continuité usuelle.
On peut astreindre $a$ à un ensemble plus petit. On définit alors la continuité comme étant sur cet ensemble.
Homéomorphisme
Un homéomorphisme $f:E\to F$ entre deux espaces topologiques (par exemple $E=F=\C$) est une bijection continue et de réciproque continue.
En particulier, $f$ envoie ouvert sur ouvert. En effet, si $U_F$ est un ouvert de $F$, alors en particulier c'est un voisinage de chacun des points de $U_F$ et donc comme $f^{-1}(U_F)$ vérifie également cette propriété (par continuité) alors $f^{-1}(U_F)$ est ouvert. De même, $f(U_E)$ est un ouvert de $F$ pour tout ouvert $U_E$ de $E$.

Compacité
La dernière notion que nous définirons est celle de compacité.
Une partie $A$ de $\C$ est compacte si pour toute suite $(a_n)_{n\in \mathbf{N}}$ à valeurs dans $A$, il existe une sous-suite convergente dans $A$.
On peut montrer que dans $\C$ les parties compactes sont les parties fermées et bornées.
On utilisera également l'autre caractérisation des parties compactes : $A\subset \C$ est compacte si, et seulement si, de tout recouvrement $(U_n)_{n\in\mathbf{N}}$ de $A$ par des ouverts, il existe un sous-recouvrement fini : $(U_{\varphi(n)})_{n\leq N < \infty}$.
Analyse complexe élémentaire
On va se munir de quelques résultats classiques d'analyse complexe. Je vais tout de même définir les termes « holomorphe » et « analytique ».
Fonction holomorphe et analytique
Soit $f : V\to\newcommand{C}{\mathbf{C}}\C$ définie sur un voisinage $V$ de $a\in \C$. $f$ est dite holomorphe en $a$ si la limite :
existe et est finie. On appelle alors ce nombre le nombre dérivé de $f$ en $a$.
Nous verrons que contrairement à l'analyse réelle, c'est une propriété très forte.
$f$ est dite analytique en $a$ s'il existe $r>0$ (tel que $B_a(r)\subset V$) et une suite $(c_n)_{n\in \mathbf{N}}$ de nombres complexes tels que :
On appelle série entière de variable $x$ une série formelle de la forme $\displaystyle \sum_{n\geq 0}c_nx^n$.
On remarquera que si $f$ est analytique en $a$ alors elle est infiniment dérivable en $a$.
Formule intégrale de Cauchy
On va se donner ce résultat d'analyse complexe pour la suite du tutoriel.
Soit $U$ un ouvert connexe1 de $\C$. Si $f$ est holomorphe sur $U$ alors $f$ est analytique sur $U$.
De plus, pour tout $z\in U$, en notant $r$ la distance euclidienne de $z$ à $\C-U$2, on a :
avec
où $C_p$ est le cercle orienté positivement de centre $z$ et de rayon $\rho$ inclus dans $U$.
En particulier, si $f:\C\to\C$ est holomorphe sur $\C$ tout entier, alors elle possède un développement en série entière valable pour tout $z\in\C$.
Maintenant que nous avons ces outils élémentaires d'analyse et de topologie, nous pouvons nous attaquer pleinement à l'étude de la sphère $\mathbf{S}^2$.