Nous avons vu dans les chapitres précédents quelques méthodes permettant de trouver les solutions des équations. Mais hélas, toutes les équations ne sont pas résolubles de façon exacte, c’est-à-dire que l’on ne peut pas les exprimer par une formule composée d’opérations classiques.
Dans ce cas, tout n’est cependant pas perdu. À défaut d’avoir une formule exacte, on peut chercher une valeur numérique approchée. Dans ce chapitre, nous allons voir deux méthodes de base permettant de trouver une approximation aussi précise que l’on veut des solutions.
Comme pour le chapitre précédent, nous allons utiliser quelques résultats d’analyse et d’étude des fonctions réelles. Si vous ne les connaissez pas, soit courrez consulter un cours sur les fonctions, soit croyez sur parole tout ce que je vais dire (c’est risqué).
Tableaux de variations
Nous avons vu que la façon la plus générale de présenter une équation est la suivante :
où est une fonction réelle. À partir de là, l’analyse, qui est la branche des mathématiques dans laquelle on étudie les fonctions réelles (et plein d’autres choses), nous offre toutes sortes d’outils permettant d’étudier les variations de .
Ce qui va nous intéresser pour la résolution des équations ce sont les tableaux de variation. Ce sont des tableaux dans lesquels on récapitule les intervalles de croissance et de décroissance de la fonction. En voici un :
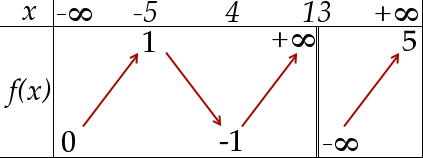
Nous n’expliquerons pas dans ce cours comment obtenir ces tableaux de variations. Si vous voulez en savoir plus, reportez-vous à un cours sur les fonctions.
Le tableau ci-dessus s’interprète de la façon suivante :
- en la fonction tend vers 0 et elle est croissante de à -5 où elle vaut 1 ;
- de -5 à 4, la fonction est décroissante et vaut -1 en 4 ;
- de 4 à 13 elle est croissante et tend vers en 13 où elle n’est pas définie ;
- de 13 à elle est croissante, elle tend vers en 13 et vers 5 en .
En clair, son graphe ressemble à ceci :
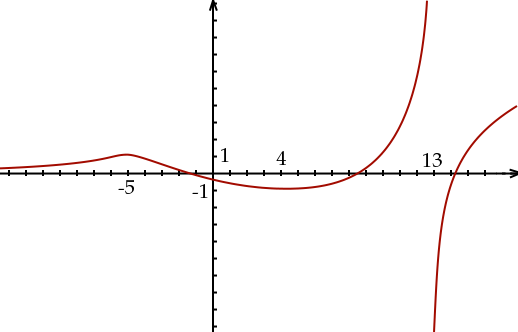
On peut donc en déduire que notre équation possède exactement trois solutions !
- La première solution se trouve entre -5 et 4.
- La deuxième solution se trouve entre 4 et 13.
- La troisième solution se trouve entre 13 et .
Rappelez-vous que les solutions de l’équation correspondent aux nombres pour lesquels la fonction vaut 0, c’est-à-dire aux points où son graphe croise l’axe horizontal.
En clair, pour chaque intervalle sur lequel la fonction est monotone (c’est-à-dire soit croissante, soit décroissante), il suffit de regarder les valeurs qu’elle prend aux bornes : si une de ces valeur est positive et l’autre négative, alors c’est que la fonction est passée par 0 entre les deux.
En réalité, ce raisonnement n’est juste qu’à condition que la fonction soit continue, c’est-à-dire qu’elle ne fasse pas de décrochages lui permettant de sauter du positif au négatif sans passer par 0. Mais rassurez-vous, dans 99% des cas classiques, les fonctions sont bien continues.
Nous avons donc cerné nos trois solutions dans trois intervalles. Alors bien sûr, ce n’est pas encore très précis, mais nous allons voir dans les sections suivantes comment se rapprocher de plus en plus de ces solutions.
Méthode de dichotomie
Une fois que l’on connait un intervalle sur lequel la fonction est croissante ou décroissante et qui passe par zéro, il nous reste à le localiser. Pour cela, la méthode la plus élémentaire est la méthode dichotomique.
Prenons donc une fonction définie entre deux nombres et comme ceci :
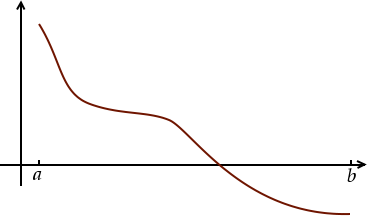
Ici la fonction est décroissante, mais ce que nous allons dire marcherait aussi bien si elle était croissante. Au début, tout ce que nous savons, c’est que la solution de notre équation se trouve entre et . Schématisons ceci par une zone verte que nous allons réduire pas à pas :
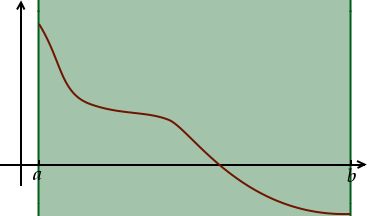
Nous allons maintenant regarder la valeur de la fonction au milieu de l’intervalle, c’est-à-dire pour la valeur moyenne . Il y a alors deux cas de figure :
- si la fonction est positive, c’est que le zéro se trouve dans la deuxième moitié de l’intervalle ;
- si au contraire elle est négative, alors le zéro se trouve dans la première moitié de l’intervalle .
Dans notre exemple, nous sommes dans le premier cas de figure :
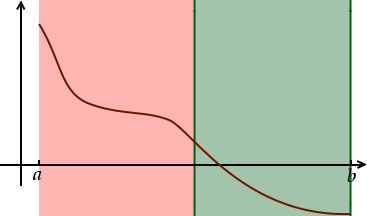
La zone dans laquelle notre zéro se trouve est donc divisée par deux. Il n’y a plus qu’à répéter le même processus avec le nouvel intervalle pour se rapprocher encore plus de notre zéro :
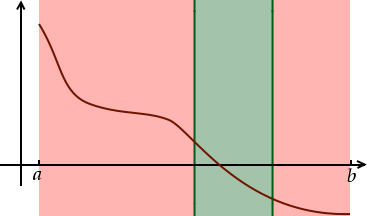
Et voici la troisième étape :
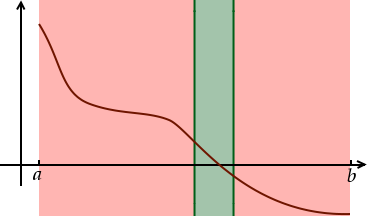
Et ainsi de suite, à chaque étape on coupe notre intervalle en deux et on garde celui des deux aux bornes duquel la fonction prend des valeurs de signes opposés.
Et quand est-ce qu’on s’arrête ?
Tout dépend de la précision que vous souhaitez. Si par exemple vous voulez connaître la solution avec deux chiffres après la virgule, il faut recommencer jusqu’à ce que l’intervalle soit plus petit que 0,01. Et si vous voulez 10 chiffres après la virgule, il faudra être plus persévérant et continuer jusqu’à ce que l’intervalle soit plus petit que 0,0000000001.
Méthode de la fausse position
La méthode de la fausse position ressemble beaucoup à la méthode dichotomique que nous venons de voir. Prenons un exemple pour comprendre son fonctionnement. Nous partons de la même façon d’une fonction monotone sur un intervalle qui s’annule à un endroit que nous cherchons.

Mais au lieu de couper notre intervalle en deux parts égales, nous allons tracer une ligne droite entre les deux points extrêmes de la fonction, et nous allons effectuer le découpage à l’endroit où cette droite passe par 0.
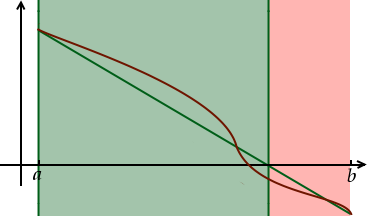
Comme pour la méthode dichotomique, on élimine alors le morceau qui ne nous intéresse pas en regardant la valeur de la fonction au point de coupage.
En fait, la méthode consiste à faire comme si la fonction allait en ligne droite. Si c’était le cas, alors cette construction nous donnerait la solution du premier coup, mais comme la fonction ne suit en général pas une droite, la position que l’on trouve est une « fausse position » de la solution, d’où le nom de la méthode. Cette méthode part du principe qu’avec cette construction, on a plus de chance de tomber proche de la racine que si on se contente simplement de prendre le point du milieu comme dans la méthode dichotomique.
Dans l’exemple ci-dessus, pas de chance, c’est le petit morceau qui s’en va. Pour l’instant, cette méthode semble moins efficace que la méthode par dichotomie. Mais regardons l’étape suivante :

Cette fois-ci, on a enlevé un gros morceau et on s’est beaucoup rapproché de la solution. Il ne reste plus qu’à répéter le même processus autant de fois qu’on le souhaite pour se rapprocher de plus en plus de la solution.
Mais alors finalement, quelle est la meilleure méthode ? La dichotomie ou la fausse position ?
Chacune a ses avantages et ses inconvénients.
Le principal problème de la méthode de la fausse position, c’est que la longueur de l’intervalle vert ne se rapproche pas forcément de zéro. En effet, il est fréquent qu’au bout d’un certain nombre d’étapes, l’une des bornes de l’intervalle vert ne bouge plus et c’est l’autre borne qui se rapproche toute seule de la solution. Essayez par exemple la méthode avec une fonction de la forme suivante :

Vous allez voir que la borne de droite ne bouge jamais : seule la borne de gauche se rapproche de la solution. Cela rend les choses plus difficile pour savoir à quelle distance on se trouve de la solution. Si on veut avoir une précision de deux chiffres après la virgule, dans la méthode dichotomique, il suffit d’attendre que l’intervalle soit plus petit que 0,01, mais ici, il est possible que l’intervalle reste toujours plus grand que cette valeur.
Mais la méthode de la fausse position a tout de même un gros avantage sur la dichotomie, c’est que celle des deux bornes qui se rapproche de la solution s’en rapproche beaucoup plus vite ! Autrement dit, il est possible d’avoir une précision bien plus grande en moins d’étapes.
En bref, avec la méthode de la fausse position on a une meilleure précision, mais il est plus difficile de savoir quelle est cette précision, tandis que la dichotomie donne une précision moindre, mais on sait exactement où on en est.
Il existe tout de même des moyens de savoir à peu près à quelle distance de la solution on se trouve avec la méthode de la fausse position. Mais c’est plus complexe et moins direct.
Il existe de nombreuses autres méthodes permettant d’approcher numériquement les solutions d’une équation. On peut par exemple citer la méthode de la sécante ou la méthode de Newton. Trouver des méthodes qui s’approchent de plus en plus vite des solutions de nos équations est un défi pour les mathématiciens, les plus efficaces d’entre-elles peuvent être extrêmement complexes à élaborer et à étudier.