En octobre 2017, Mathy Vanhoef a publié un papier exposant une vulnérabilité dans les implémentations du protocole WPA2. Aujourd’hui utilisé pour la plupart des communications Wi-Fi, il veille au chiffrement des données transmises entre la borne Wi-Fi (le point d’accès) et le client (ordinateur, smartphone, etc.).
La vulnérabilité découverte permet de mener des attaques dites KRACK contre ces communications Wi-Fi et d’en décrypter le contenu sans même connaître la clé de chiffrement. Dans la suite, nous verrons comment fonctionne WPA2 et en expliquerons la faille. Cet article se veut un intermédiaire entre la technicité du papier et la superficialité des médias. Aucun aspect pratique n’y sera abordé. Pour en comprendre au mieux le contenu, il est recommandé d’avoir des notions de base en réseau, et notamment de connaître celle de protocole.
Le protocole WPA2
Une communication Wi-Fi fait intervenir deux acteurs :
- Le point d’accès, ou AP (par exemple votre box) ;
- Le client (votre smartphone, ordinateur…).
Chacun peut contacter l’autre et est donc en mesure à la fois de chiffrer les données et de les déchiffrer. Cette sécurité est mise en oeuvre avec l’algorithme AES, aujourd’hui considéré comme le plus sûr. AES est dit symétrique : le chiffrement et le déchiffrement sont effectués avec une seule et même clé, contrairement à RSA par exemple.
4-way handshake
Pour échanger de manière sécurisée, les deux composants procèdent à une phase d’initialisation, appelée 4-way handshake, durant laquelle ils se mettent d’accord sur une clé de chiffrement. Cette dernière se base sur une information secrète et connue des deux acteurs, appelée Pairwise Master Key (PMK). Dans le cas de WPA2 Personal (par opposition à WPA2 Entreprise), il est question du mot de passe étiqueté sur votre box. Le transfert normalement sécurisé de la clé maître se fait donc par l’humain recopiant le code. Dans la version Entreprise, le partage du la clé se fait avec une authentification 802.1x.
Ce secret dure en principe dans le temps (on change rarement le mot de passe de son Wi-Fi). On souhaite donc l’exposer le moins possible, puisqu’un vol pourrait affecter à notre insu toutes nos communications futures. Au lieu de cela, on construit à chaque connexion1 une clé temporaire (Pairwise Transient Key, PTK) à partir de cinq éléments :
- PMK ;
- Nonce AP ;
- Nonce client ;
- Adresse MAC de l’AP ;
- Adresse MAC du client.
Un nonce est un nombre arbitraire à usage unique (on l’obtient généralement par tirage aléatoire). Ici, on en a deux : un généré par le point d’accès, l’autre par le client.
En plus de faire office de secret, la clé maître joue un rôle de signature. En construisant la même PTK que moi, le point d’accès me prouve qu’il connait la PMK et me rassure sur son identité. Un attaquant ne peut donc pas se faire passer pour lui (sauf s’il connait la clé maître, auquel cas tout est fichu). Nous reviendrons plus tard sur l’utilité des nonces. Comme les composants communiquent, chacun connait déjà l’adresse MAC de l’autre.
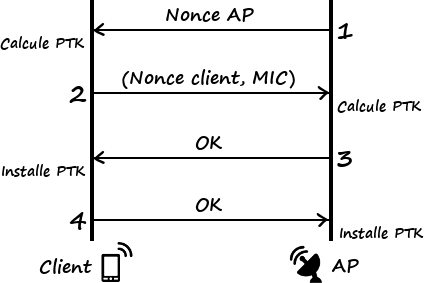
Tout l’objectif du 4-way handshake est de construire cette clé temporaire et de la faire connaître des deux acteurs (rappelez-vous en effet la symétrie d’AES). Comme indiqué par son nom, il consiste en quatre étapes :
- Point d’accès vers client : l’AP génère un nonce et l’envoie au client.
- Client vers point d’accès : le client génère un nonce ainsi que la PTK, qu’il envoie à l’AP avec un code MIC, lequel permet simplement de détecter la corruption potentielle du message.
- Point d’accès vers client : utilisons PTK (et envoi d’informations additionnelles).
- Client vers point d’accès : très bien, nous pouvons commencer à échanger.
Le chiffrement
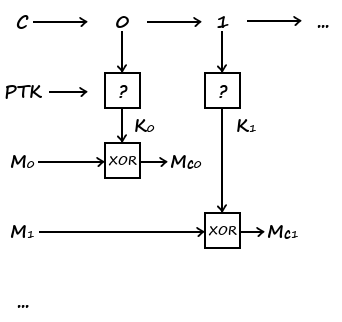
Une fois le 4-way handshake terminé et la clé temporaire installée, le chiffrement s’effectue de manière simplifiée comme suit. Chaque acteur initialise un compteur $C$ à la même valeur et les deux l’incrémenteront du même pas. Considérons l’exemple d’un message $M$ envoyé par le client au point d’accès :
- Récupérer la valeur $i$ de $C$ et incrémenter $C$ ;
- Générer une clé de chiffrement $K_i$ à partir de $i$ et de la PTK ;
- Calculer le message chiffré $M_c = M \oplus K_i$, avec $\oplus$ =
XOR.
Pour le troisième point, on supposera que le message aura été au préalable découpé en blocs $M_i$ de même taille que $K_i$. Le résultat est alors $M_{ci}$, la version chiffrée de $M_i$.
La valeur d’origine du compteur n’a pas à être secrète. D’une certaine manière, seule la PTK assure que $K_i$ est inconnue de l’attaquant. Comme nous le verrons dans la section suivante, le compteur, lui, permet d’éviter que l’attaquant déduise la clé temporaire à partir des messages chiffrés.
Le point d’accès déchiffre alors le message de cette manière :
- Récupérer la valeur $i$ de $C$ et incrémenter $C$ ;
- Générer une clé de (dé)chiffrement $K_i$ à partir de $i$ et de la PTK ;
- Retrouver $M$ à partir de $M = M_c \oplus K_i$.
La dernière équation se détaille en :
Il est très important de noter que les valeurs $i$ de $C$ ne servent qu’une seule fois sur chaque acteur, c’est-à-dire que les $K_i$ sont uniques pour une clé temporaire donnée. Nous verrons dans la section suivante ce qu’il se passe quand ce n’est pas le cas.
-
Comprendre « à chaque fois que vous rejoignez le réseau via ce point d’accès ». ↩
La faille
Comme indiqué en introduction, plusieurs attaques ont été découvertes. Vous pouvez en retrouver une liste dans la section « Assigned CVE identifiers » de cette page. Je me contenterai ici d’introduire les principes généraux sous-jacents à ces attaques.
Quand le point d’accès ne reçoit pas le dernier message du handshake, il conclut que le client n’a pas réceptionné le troisième et le renvoie donc. Et c’est là où le bât blesse. Mathy Vanhoef a découvert que le client réinstallait alors la clé temporaire, réinitialisant par la même occasion le compteur $C$. Il réexpédie également le message 4, suite auquel le point d’accès réinitialise également son compteur, sans changer de PTK.
Autrement dit, en se plaçant au milieu des communications (man-in-the-middle attack), un attaquant peut à sa guise réinitialiser les compteurs du client et du point d’accès en renvoyant le message 3 au premier. Ainsi, il brise l’unicité du couple (PTK, $i$) et obtient des messages chiffrés avec la même clé1 :
Sans même connaître la clé, il lui est alors possible de retrouver $M_1$ et $M_2$ (les messages d’origine) avec une méthode appelée crib-dragging.
On comprend ici le rôle des nonces échangés lors du 4-way handshake : ils permettent l’unicité de la PTK et donc du couple (PTK, $i$) entre deux connexions. Dans le cas contraire, on pourrait se retrouver à la fin du 4-way handshake avec le même $K_0$. La réinstallation de la clé (la faille) a donc le même effet que si on générait plusieurs fois la même clé temporaire.
Certaines propriétés du 4-way handshake ont été prouvées formellement, comme le fait que la clé temporaire reste privée et que les identités du client et du point d’accès sont assurées. Seulement, le modèle n’inclue pas la phase d’installation de la PTK, à l’origine de la faille. D’ailleurs, tous les systèmes d’exploitation ne sont pas uniformément vulnérables, selon leur implémentation de cette phase.
Crib-dragging
Commençons par remarquer que $M_{1c} \oplus M_{2c} = M_1 \oplus M_2$ :
Le programme Python suivant confirme cette propriété :
1 2 3 4 5 6 7 8 9 10 11 12 13 | >>> def xor_str(s, t): ... return ''.join(chr(ord(a) ^ ord(b)) for a, b in zip(s,t)) ... >>> m1, m2, k = 'a', 'b', 'c' >>> mc1, mc2 = xor_str(m1, k), xor_str(m2, k) >>> mc1, mc2 ('\x02', '\x01') >>> xor_str(mc1, mc2) '\x03' >>> xor_str(m1, m2) '\x03' >>> xor_str(mc1, mc2) == xor_str(m1, m2) True |
L’attaquant obtient donc facilement $M_1 \oplus M_2$. Remarquons que s’il connait $M_1$, il détermine $M_2$ avec cette équation :
1 2 3 4 5 6 7 8 | >>> m1, m2, k = "Le sens de la vie est", "Ca passe ou ça KRACK!", "abcdefghijklmnopqrstu" >>> mc1 = xor_str(m1, k) >>> mc2 = xor_str(m2, k) >>> mc_xor = xor_str(mc1, mc2) >>> xor_str(m1, mc_xor) 'Ca passe ou ça KRACK!' >>> xor_str(m2, mc_xor) 'Le sens de la vie est' |
Mais il y a peu de chances que l’attaquant connaisse un des deux messages dans son intégralité. Par contre, il peut faire des hypothèses sur leur contenu. Par exemple, si les messages sont en français, ils comporteront probablement des mots comme « et » ou « le ». Regardons ce qu’il se passe s’il parvient à positionner un tel mot correctement :
1 2 3 | >>> m_hack = "..................est" >>> xor_str(m_hack, mc_xor) '!*.-*3.kj${b¨ox\x0c\x19OCK!' |
On retrouve la fin du second message ! Seulement, l’attaquant ignore que le mot « est » apparaît à la toute fin. Qu’à cela ne tienne ! Il lui suffit de tester toutes les positions :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | >>> def cribdrag(mc_xor, word): ... for i in range(len(mc_xor) - len(word) + 1): ... # Pour les Pythonistes : on préfèrera utiliser `yield` ... # mais `print` rend le code plus accessible ... # `repr` permet d'afficher les caractères non imprimables sous forme de code ... print(repr(xor_str(word, mc_xor[i:i+len(word)]))) ... >>> cribdrag(mc_xor, "est") 'jwt' 'asw' 'epp' 'fwi' 'ant' 'xs1' 'e60' ' 7~' '!y!' 'o&8' '0?ò' ')õ5' 'ã2"' '$%V' '3QC' 'GD\x15' 'R\x12R' '\x04UL' 'CK!' |
Il ne reste alors plus qu’à considérer des mots dérivant probablement d’une de ces suites de lettres et de recommencer avec ces mots. Par exemple, CK! fait penser à KRACK!2. Repassons donc le crible :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | >>> cribdrag(mc_xor, "KRACK!") 'DVA@O<' 'ORBGV!' 'KQE^Kd' 'HV\\C\x0ee' 'OOA\x06\x0f+' 'VR\x04\x07At' 'K\x17\x05I\x1em' '\x0e\x16K\x16\x07§' '\x0fX\x14\x0fÍ`' 'A\x07\rÅ\nw' '\x1e\x1eÇ\x02\x1d\x03' '\x07Ô\x00\x15i\x16' 'Í\x13\x17a|@' '\n\x04ct*\x07' '\x1dpv"m\x19' 'ie est' |
Et on répète le procédé. La dernière ligne nous indique un mot se terminant par ie. On peut alors récupérer la liste des mots les plus courants satisfaisant cette condition.
Pour des informations complémentaires et des conseils sur comment faire face à ce risque, je vous recommande ce site. J’ai également consulté les ressources suivantes pour écrire cet article :
Je ne suis pas parvenu à déterminer la licence du logo.
Je remercie vivement Saroupille pour la validation.