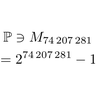À leurs débuts, les ordinateurs ont été surtout des outils pour le calcul. Désormais, les outils informatiques ont aussi une place grandissante comme assistants pour effectuer des démonstrations mathématiques (on parle aussi de preuves), que ce soit par des mathématiciens ou des informaticiens. Les premiers les utilisent pour des preuves mathématiques, alors que les seconds sont plus intéressés par l’écriture de programmes prouvés corrects.
Dans les deux cas, ces outils sont d’une grande aide pour aider à construire des preuves et les vérifier automatiquement. Cette vérification automatisée permet d’atteindre des niveaux de confiance supérieurs aux preuves vérifiées par des humains. Il est aussi possible de traiter des problèmes dont la taille rend un traitement manuel trop laborieux, voire impossible.
Ces outils appliquent les règles logiques sans faillir, mais ont aussi très peu d’imagination : soit ils prouvent seuls des problèmes d’une forme spécifique et bien connue, soit ils savent vérifier des preuves complexes, mais il faut leur fournir tous les détails avec minutie. En effet, contrairement aux humains, où il suffit de détailler grossièrement la démonstration et laisser au lecteur le soin d’éclaircir les zones d’ombre, les outils automatiques tendent à avoir besoin des moindres détails du raisonnement pour faire leur travail de vérification.
Dans cet article, nous verrons sur un exemple à quoi ressemblent les mathématiques assistées par ordinateur, en démontrant des théorèmes sur un mini-univers mathématique constitué des points cardinaux et de transformations géométriques. L’outil que nous utiliserons est le prouveur interactif Coq. En d’autres termes, il s’agit d’un logiciel qui permet d’écrire précisément des théorèmes et d’en construire des preuves vérifiées en interagissant avec le système de vérification de preuve intégré à l’outil.
Cet article devrait être accessible à toute personne familière avec la géométrie élémentaire et les techniques de base de la démonstration.
Définissons notre mini-univers mathématique
Pour les besoins de cet article, nous définissons un mini-univers mathématique. L’objectif est d’avoir un exemple relativement simple et circonscrit pour faciliter la compréhension. Coq en lui-même peut être utilisé pour des projets bien plus complexes comme nous le verrons à la fin.
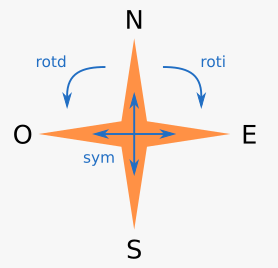
Notre mini-univers mathématique est celui des points cardinaux : nord, sud, est et ouest et de quelques-unes de leurs transformations : rotations d’un quart de tour et symétrie par rapport à l’origine.
À quoi ressemble Coq ?
Pour expliquer notre mini-univers mathématique à Coq, il faut interagir avec lui à l’aide de commandes. Une manière conviviale de le faire est d’utiliser une interface graphique telle que CoqIde, qu’on voit ci-dessous.
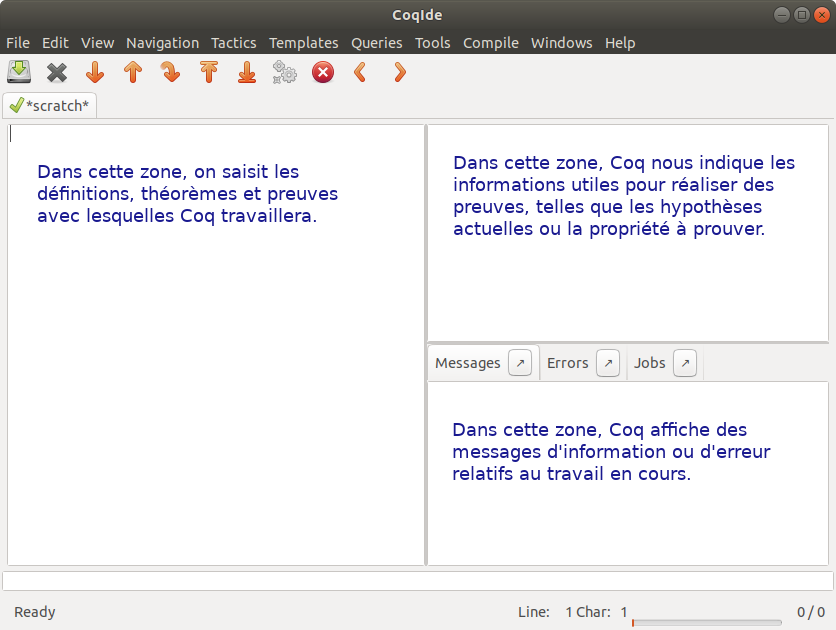
La zone de gauche est celle où on saisit les commandes pour Coq. Quand on commence à travailler, cette zone est vide. Autrement dit, Coq ne sait rien de particulier au départ. Il a seulement connaissance des règles logiques fondamentales.1 C’est là que toutes les commandes de cet article seront saisies.
À mesure qu’on saisit des commandes dans la zone de gauche, Coq exigera qu’on démontre certaines choses, qu’il affichera dans la zone en haut à droite. Des informations ou erreurs concernant les dernières commandes saisies sont affichées dans la zone en bas à droite.
Objets de notre mini-univers
Comme nous l’avons dit avant, Coq ne sait pas grand chose. En particulier, il ne sait pas ce qu’est une rose des vents, et encore moins ce qu’est un point cardinal. Expliquons-lui tout cela :
Inductive point := N | S | E | O.
Il faut lire cette ligne comme suit : « Je définis un type d’objets (commande Inductive) nommé point ; les objets de ce type sont de la forme N, S, E ou O et aucune autre. »
Ensuite, il faut définir nos transformations géométriques :
- la rotation d’un quart de tour directe
rotd, - la rotation d’un quart de tour indirecte
roti, - la symétrie centrale
sym.
En Coq, cela se traduit comme cela :
Variable rotd : point -> point.
Variable roti : point -> point.
Variable sym : point -> point.
Pour comprendre ces lignes, prenons en exemple la première ligne. Elle signifie la chose suivante : « Je définis un objet (commande Variable) nommé rotd ; cet objet est une transformation qui à un objet de type point associe un autre objet de type point (ce qu’on note point -> point). »
Propriétés de nos transformations
Ces quelques lignes ont expliqué à Coq quels étaient les objets de notre univers, mais il ne sait toujours pas quoi en faire ! Il ne sait pas ce qu’est une symétrie ou une rotation pour le moment, mais seulement qu’il s’agit de transformations de points. Définissons quelques propriétés pour décrire l’effet de ces transformations (en espérant qu’elles soient suffisantes pour notre usage).
Notre première propriété concerne la symétrie ; on souhaite expliquer à Coq que si on fait une symétrie, on peut faire marche arrière en effectuant la même symétrie. Autrement dit, si un point est le symétrique d’un autre, alors cet autre point est le symétrique du premier et réciproquement. Plus formellement, on pourrait dire qu’étant donnés deux points A et B quelconques, il est équivalent de dire que A est le symétrique de B ou B est le symétrique de A. C’est ce que nous allons expliquer à Coq :
Axiom sym_inv_sym: forall p1 p2, sym p1 = p2 <-> sym p2 = p1.
Ici, on utilise la commande Axiom qui permet d’écrire une propriété qui sera considérée vraie sans démonstration par Coq. On lui donne ensuite un nom, ici sym_inv_sym et on écrit la propriété dans un langage proche de la notation mathématique habituelle, avec ici le quantificateur universel forall, des égalités utilisant sym et l’équivalence <->.
On définit de manière similaire que les rotations directe et indirecte sont les réciproques l’une de l’autre :
Axiom roti_inv_rotd: forall p1 p2, rotd p1 = p2 <-> roti p2 = p1.
Enfin, il nous manque une relation entre la rotation et la symétrie. Coq ne sait pas pour le moment qu’il s’agit de quarts de tours, et que donc deux quarts de tour font un demi-tour, c’est-à-dire le même effet qu’une symétrie. En Coq, j’ai choisi de l’écrire comme ça :
Axiom rot2_sym: forall p, rotd (rotd p) = sym p.
On peut le lire de la manière suivante : « rot2_sym est un axiome affirmant que pour tout p (sous-entendu de type point), le point obtenu par la rotation directe du point obtenu par rotation directe de p est le symétrique de p. »
Relations entre points
Si nous avons expliqué à l’ordinateur comment se comportent globalement nos transformations, nous n’avons encore rien dit sur leurs liens avec les points. Nous connaissons bien les positions relatives des points cardinaux : le nord en haut, le sud en bas, l’est à droite, l’ouest à gauche. Coq ne sait évidemment pas tout ça, il faut donc lui expliquer.
Faisons appel à notre intuition pour en dire le minimum possible sur les relations entre les points, afin d’éviter des redondances. Si on en dit assez, il devrait être alors possible de démontrer tout ce que l’on souhaite sans trop d’effort.
Le plus évident est sûrement que le nord est à l’opposé du sud et que l’est est à l’opposé de l’ouest. Traduisons cela par des symétries : le sud est le symétrique du nord et l’ouest est le symétrique de l’est. En Coq, cela fera de nouveaux axiomes :
Axiom sym_n_s: sym N = S.
Axiom sym_e_o: sym E = O.
Enfin, il faut indiquer à Coq l’orientation relative des axes N-S et E-O. Nous exprimons cela en disant que l’ouest est obtenu par rotation en sens direct du nord :
Axiom rotd_n_o: rotd N = O.
Toutes ces informations données soigneusement à Coq devraient être suffisantes pour démontrer quelques théorèmes de notre mini-univers mathématique.
- En pratique, quelques bibliothèques sont chargées automatiquement et ajoutent quelques connaissances supplémentaires, mais nous n’y faisons pas appel dans cet article.↩
Démontrons des théorèmes !
Il existe plein de théorèmes relativement intéressants dans ce mini-univers, mais nous nous contenterons de quelques exemples pour montrer progressivement à quoi ressemblent les démonstrations avec Coq.
Une petite égalité sans prétention
Pour commencer, attaquons-nous à quelque chose en apparence évident : par rotation directe d’un quart de tour de O, on obtient S. C’est évident quand on regarde la rose des vents, mais pour Coq, puisque ce n’est pas un axiome, c’est un théorème qu’il faut démontrer.
Les théorèmes s’énoncent avec la commande Theorem, on leur donne un nom, puis on écrit l’énoncé à la suite, qu’on conclut par un point.
Theorem rotd_o_s: rotd O = S.
Ensuite, il faut démontrer ce théorème. Sur une rose des vents, « ça se voit ». Mais pour Coq, il faut procéder étape par étape, en utilisant les axiomes. On démarre la démonstration à l’aide de la commande Proof. Quand on procède ainsi, Coq nous parle en retour (comme avec toutes les commandes, même si je ne l’ai pas mentionné avant), en indiquant ce qu’il faut prouver :
1 subgoal
______________________________________(1/1)
rotd O = S
Ces quelques mots nous indiquent que nous avons un seul sous-objectif de preuve, et il s’agit évidemment du théorème tel qu’énoncé avant. Comment procède-t-on pour démontrer cela ?
La théorie mathématique derrière Coq nous permet d’écrire des preuves en enchaînant des tactiques. Ces tactiques ont pour but de transformer le sous-objectif courant jusqu’à tomber sur la propriété toujours vraie (True en Coq), ce qui conclut la démonstration. Par rapport à une démonstration usuelle, Coq procède à l’envers : plutôt que de partir de quelque chose de vrai et d’effectuer des déductions pour aboutir au résultat souhaité, on part du résultat souhaité pour aboutir à quelque chose dont il est la conséquence.
Voilà une manière informelle d’écrire la preuve dans le sens habituel :
- on part de l’axiome disant que deux rotations donnent une symétrie directe ;
- on l’applique à N : rotd (rotd N) = sym N ;
- on remplace rotd N par O à gauche ;
- on remplace sym N par S à droite ;
- on obtient alors rotd O = S, qui est ce qu’il fallait démontrer.
En Coq, on remonte des conséquences vers les causes (les portions en parenthèses étoilées sont des commentaires ignorés par Coq) :
(* On commence la preuve. L’objectif est : rotd O = S. *)
Proof.
(* On réécrit en remplaçant S par sym N en utilisant l’axiome. L’objectif est désormais : rotd O = sym N. *)
rewrite <- sym_n_s.
(* On réécrit en remplaçant O par rotd N. L'objectif est maintenant : rotd (rotd N) = sym N. *)
rewrite <- rotd_n_o.
(* On applique l’axiome, ce qui termine la preuve car il est toujours vrai. Il n'y a plus d'objectif. *)
apply rot2_sym.
(* quod erat demonstrandum : le théorème est démontré, on passe à la suite *)
Qed.
Il y a dans cette preuve deux tactiques différentes :
rewrite, qui correspond au remplacement d’un terme par un autre, et qui est pratique pour transformer des expressions,apply, qui sert à appliquer des théorèmes (l’effet exact dépend de la forme du théorème, ici cela termine la preuve).
Il a bien fallu écrire à Coq tous les détails, mais au fur et à mesure de l’avancée de la preuve et jusqu’à sa conclusion, nous avons la garantie que ce que nous avons écrit est juste. Les preuves fausses ne peuvent pas être conclues avec Coq : la commande Qed déclencherait dans ce cas une erreur expliquant qu’il y a encore des objectifs à prouver.
Un théorème un peu plus abstrait
La symétrie est involutive, cela signifie qu’elle est sa propre réciproque, et que donc l’appliquer deux fois d’affilée ramène au point initial. C’est une propriété relativement évidente, car c’est une conséquence d’un de nos axiomes, mais il faut le prouver pour que Coq en ait la connaissance.
Voici l’énoncé du théorème en Coq :
Theorem sym_involutive: forall p, sym (sym p) = p.
La preuve est commentée ci-dessous :
(* On commence la preuve. L’objectif est : forall p, sym (sym p) = p *)
Proof.
(* Le théorème contient "pour tout p", la tactique intro permet de considérer un p quelconque. *)
(* L'objectif devient : sym (sym p) = p. *)
intro p.
(* On applique le théorème sur la symétrie : Coq échange (sym p) et p *)
(* L'objectif devient : sym p = sym p *)
apply sym_inv_sym.
(* Rien n'est évident pour Coq, on prouve cela par réflexivité de l'égalité. *)
reflexivity.
(* La démonstration est finie. *)
Qed.
Quelques autres théorèmes
On peut démontrer de nombreux petits théorèmes dans notre mini-univers. Par exemple, quatre rotations directes reviennent au point de départ :
Theorem rotd4: forall p, rotd (rotd (rotd (rotd p))) = p.
Un autre exemple disant que d’une certaine manière, les symétries changent le sens des rotations :
Theorem sym_rotd_roti: forall p, sym (rotd p) = roti p.
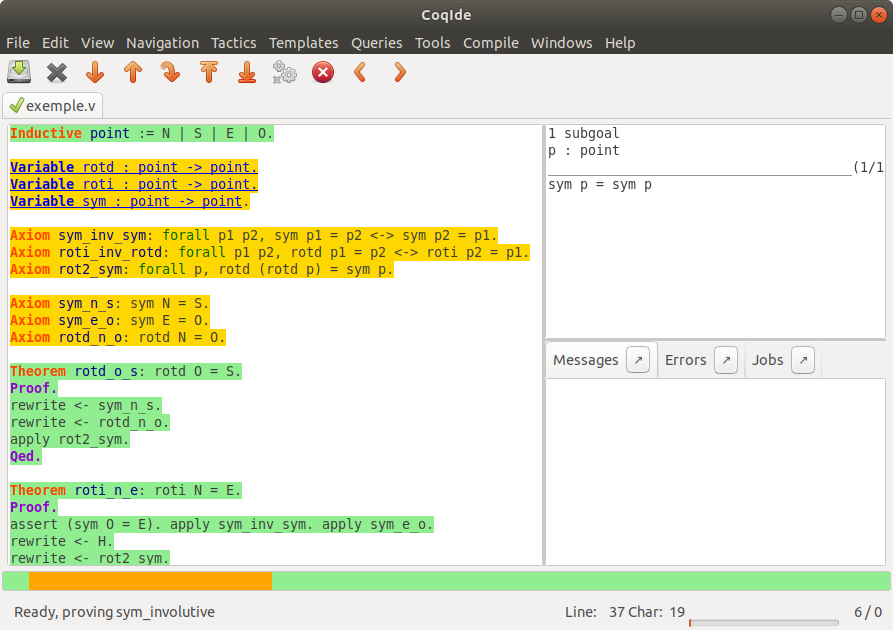
Voilà, vous avez un aperçu de comment certains logiciels peuvent être des assistants utiles pour faire des mathématiques !
L’exemple pris dans cet article est tout simple, il ne s’agit que d’un petit jouet mathématique. Coq est cependant un outil apte à la résolution de problèmes bien plus sérieux. Coq a par exemple permis la formalisation du théorème des quatre couleurs, qui porte sur le coloriage de graphes. D’autres projets ambitieux utilisent Coq, comme par exemple le compilateur CompCert qui transforme du code C en assembleur de manière mathématiquement correcte.
Aller (beaucoup) plus loin
- L’article Assistant de preuve sur Wikipédia, qui cite d’autres logiciels similaires à Coq.
- Le site officiel de Coq.
- Software Foundations, une série de livres qui enseignent Coq dans le cadre de la preuve de programmes.
- Le Coq’Art, un livre pour apprendre Coq et la théorie mathématique qui se cache derrière.