Reconnaissance de chiffres manuscrits

OpenCV (pour Open Computer Vision) est une bibliothèque graphique libre spécialisée dans le traitement d’image en temps réel. Elle contient plus de 2500 algorithmes optimisés exprès pour ce type de travail. Je vous invite à vous renseigner d’avantage sur ce magnifique outil qu’est OpenCV.

Installer OpenCV

J’ai compilé depuis les sources la version 4.2.0 mais rien ne vous oblige de faire pareil. C’est pourquoi je vous propose la méthode simple avec pip.

pip

Cette méthode est assez rapide mais assurez-vous avant de bien avoir pip d’installé

python3 -m pip install --user -U opencv-python opencv-contrib-python

Avant de commencer à écrire l’algorithme qui va permettre à l’ordinateur de reconnaître un chiffre, nous allons devoir lui préparer de quoi en reconnaître un pour quand on lui en donnera. Pour cela, commençons par un ensemble d’images des chiffres de 0 à 9.

Nous allons réaliser cette partie avec getTextSize() qui va nous permettre de connaître la taille de l’image nécessaire pour chaque chiffre. Cette fonction prend 4 paramètres :

• text: dans notre cas ce sera les chiffres allant de 0 à 9 ;
• fontFace: la liste des valeurs possible est ici ;
• fontScale: un facteur de taille ;
• thickness: l’épaisseur du trait de dessin.

Créons un fichier nommé digit.py et avec l’aide de putText(), commençons à générer nos images :

#!/usr/bin/env python3
import cv2
import numpy as np

SCALE = 3
THICK = 5
WHITE = (255, 255, 255)

digits = []
for digit in map(str, range(10)):
    (width, height), bline = cv2.getTextSize(digit, cv2.FONT_HERSHEY_SIMPLEX,
                                             SCALE, THICK)
    digits.append(np.zeros((height + bline, width), np.uint8))
    cv2.putText(digits[-1], digit, (0, height), cv2.FONT_HERSHEY_SIMPLEX,
                SCALE, WHITE, THICK)
    x0, y0, w, h = cv2.boundingRect(digits[-1])
    digits[-1] = digits[-1][y0:y0+h, x0:x0+w]

    cv2.imshow(digit, digits[-1])

Maintenant notre liste digits contient 10 images des chiffres allant de 0 à 9 :

Nous pourrons plus tard utiliser ces échantillons pour les comparer à notre écriture manuscrite.

Nous allons maintenant passer au traitement d’image. Le but ici est de partir d’une image, extraire les chiffres présents dessus et les comparer à ceux générés dans la première partie.

Voici l’image de test utilisée :

Lecture de l’image

La première étape consiste à charger l’image et la convertir en noir et blanc puisque dans notre cas, la couleur importe peu et peut même nous gêner. C’est notre premier traitement.

Toujours à la suite de votre fichier digit.py :

color_test_image = cv2.imread('/chemin/vers/votre/image.png', cv2.IMREAD_COLOR)
gray_test_image = cv2.cvtColor(color_test_image, cv2.COLOR_BGR2GRAY)
cv2.imshow('test_image', gray_test_image)

Vous devriez avoir ceci:

Nettoyer l’image

Comme nous voulons extraire uniquement les chiffres de notre photo de départ, on va faire un traitement en utilisant un seuil binaire pour faire ressortir les chiffres. Les chiffres sont écrits avec de l’encre noire sur un papier blanc mais ceux que nous avons générés sont en blanc sur fond noir.

Nous allons donc reproduire le même comportement que dans notre première partie grâce à la fonction threshold() qui prend également 4 paramètres :

• src : l’image source (test_image) ;
• thresh : notre valeur de seuil ;
• maxval : valeur maximale à utiliser avec THRESH_BINARY et THRESH_BINARY_INV ;
• type : le type de seuillage à utiliser (liste des types ici).

On peut donc écrire:

# faire un seuillage binaire inversé pour faire ressortir les chiffres en blanc sur noir
ret, thresh = cv2.threshold(gray_test_image, 170, 255, cv2.THRESH_BINARY_INV)

Maintenant l’image thresh devrait ressembler à ça :

L’intérêt d’utiliser des images en noir et blanc réside aussi dans le fait de pouvoir les gérer comme des tableaux de booléens (0 noir, 1 blanc) ; on peut donc utiliser des opérations logiques (AND, OR, XOR, NAND…) pour trouver la plus haute correspondance.

La fonction de détection

Le but va être de comparer une image passée en argument et de la comparer avec nos chiffres connus générés précédemment.

La comparaison

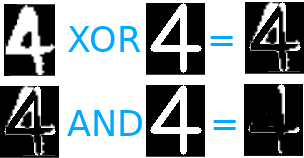
Plus le chiffre témoin est effacé, plus la correspondance sera élevée. C’est pourquoi on commence par faire un XOR (ou exclusif) sur nos deux images. Le XOR aura pour effet de conserver ce qui n’est pas commun entre les deux. Une fois fait, on peut maintenant faire un AND (et logique) qui nous donnera une image contenant uniquement la partie qui n’est pas recouverte par notre chiffre écrit. Plus cette partie est faible plus la reconnaissance est "sûre".

Ex.
Si le 4 témoin contient 400 pixel blanc, et qu’après le XOR et le AND il n’en contient plus que 74, on peut faire le calcul suivant 100 - (74 / 400 * 100) ce qui donne 81% de correspondance.

def detect(img):
    # chiffre extrait, on le compare avec notre base
    percent_white_pix = 0
    digit = -1
    for i, d in enumerate(digits):
        scaled_img = cv2.resize(img, d.shape[:2][::-1])
        # d AND (scaled_img XOR d)
        bitwise = cv2.bitwise_and(d, cv2.bitwise_xor(scaled_img, d))
        # le resultat est donné par la plus grosse perte de pixel blanc
        before = np.sum(d == 255)
        matching = 100 - (np.sum(bitwise == 255) / before * 100)
        #cv2.imshow('digit_%d' % (9-i), bitwise)
        if percent_white_pix < matching:
            percent_white_pix = matching
            digit = i
    return digit

Extraction de tous les chiffres

On va trouver tous les contours faits au stylo pour ensuite comparer chaque image avec nos images témoins et écrire la détection sur notre image en couleur.

# trouver les contours de notre image seuillée
contours, hierarchy = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)

Nous avons maintenant tous les contours de notre écriture, nous allons pouvoir isoler chaque chiffre pour le comparer :

for cnt in contours:
    # on vérifie la taille du contour pour éviter de traiter un 'défaut'
    if cv2.contourArea(cnt) > 30:
        # on récupère le rectangle encadrant le chiffre
        brect = cv2.boundingRect(cnt)
        x,y,w,h = brect
        # extraction de notre "region of interest"
        # notre roi correspond à un chiffre sur notre feuille
        roi = thresh[y:y+h, x:x+w]

        # detection
        digit = detect(roi)

        cv2.rectangle(color_test_image, brect, (0,255,0), 2)
        cv2.putText(color_test_image, str(digit), (x, y), cv2.FONT_HERSHEY_SIMPLEX, 1, (190, 123, 68), 2)

cv2.imshow('resultat', color_test_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

Nous prenons chaque roi (chiffre) extrait pour le comparer à nos images tests et nous ne retournons que la correspondance la plus forte.

Voici le résultat :

On obtient 80% de réussite ce qui n’est pas si mal, en fonction de notre écriture, on peut obtenir un pourcentage de réussite très variable.

L’algorithme dans la boucle

En faisant un copier/coller du code ci-dessus, il n’est pas forcément évident de comprendre ce qu’il se passe. Une image valant mieux que mille mots, voici visuellement ce qu’il se trame.

Pour chaque chiffre de la photo extrait, on le compare à tous les autres en procédant comme ceci :

• faire un XOR entre l’image du chiffre détecté et le chiffre témoin ;
• faire un AND entre le résultat du XOR et le chiffre témoin ;
• on compare le nombre de pixel blanc sur le chiffre témoin avant et après ;
• si le pourcentage d’effacement/recouvrement du chiffre témoin est plus élevé que le précédent, on le converse.

Exemple d’application

Reconnaître un seul chiffre peut vous paraître assez maigre comme résultat, mais libre à vous d’adapter et améliorer cet exemple d’algorithme. En utilisant exactement la même logique, vous pouvez extraire des cartes à jouer d’une image et détecter leur valeur ainsi que le symbole (♥, ♠, ♦ et ♣). Bien évidemment avec les mêmes faiblesses qu’expliquées précédemment, mais vous pouvez obtenir un résultat similaire à ça:

La seule erreur de détection sur cette image est le signe du 🂪 en haut à droite. Avec ce type d’approche, il est très difficile d’obtenir du 100% mais c’est toujours intéressant de voir des méthodes qu’un humain peut comprendre facilement, ce qui est loin d’être le cas quand on utilise des réseaux de neurones qui rend la méthode "opaque" pour nous.

Si vous voulez vous lancer, je vous conseille de commencer par des exemples simples (détection de chiffres) pour complexifier de plus en plus et arriver comme dans l’exemple ci-dessus à de la détection d’éléments plus complexes, comme des cartes à jouer.