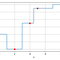
Lorsqu’on connaît les valeurs que prend une fonction seulement en certains points et qu’on souhaite lui attribuer une valeur en d’autres points, on peut effectuer ce qu’on appelle une interpolation.
La plus simple des interpolations est l’interpolation au plus proche : sur son ensemble de définition, la fonction prend la valeur du point connu le plus proche.
Exemple
Imaginons que l’on connaisse la fonction aux points suivants.
| x | f(x) |
|---|---|
| 0 | 2 |
| 2 | -2 |
| 6 | 5 |
| 8 | 9 |
| 10 | 10 |
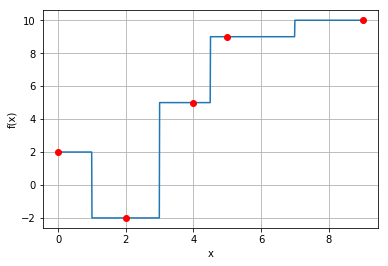
La fonction obtenue par interpolation au plus près est dans la figure ci-dessous.
Définition plus formelle
On dispose d’un ensemble de points $x_1$, …, $x_n$, rangés par ordre croissant, pour lesquels on connaît la valeur que prend la fonction $f$. Autrement dit, on connaît les valeurs $y_1 = f(x_1)$, …, $y_n = f(x_n)$.
L’interpolation au plus proche consiste à attribuer aux points inconnus la valeur du point connu le plus proche. Concrètement, la fonction $f$ est définie sur $[x_1, x_n]$ par :
Implémentation en Python
Une implémentation rudimentaire en Python se trouve ci-dessous.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 | # coding: utf-8 # In[102]: x = [0, 2, 4, 5, 9] y = [2, - 2, 5, 9, 10] # In[103]: def interpolant(x, y): def interpFn(x0): if x0 < x[0] or x0 > x[-1]: raise BaseException elif x0 == x[0]: return y[0] elif x0 == x[-1]: return y[-1] else: i2 = 0 while x0 > x[i2]: i2 += 1 i1 = i2 - 1 if x0 < (x[i1] + x[i2])/2: return y[i1] else: return y[i2] return interpFn # In[104]: f = interpolant(x, y) # In[105]: import numpy as np x0 = np.linspace(0, 9, 1000) y0 = np.zeros(1000) for i in range(1000): y[i] = f(x[i]) # In[107]: import matplotlib.pyplot as plt plt.plot(x0, y0) plt.xlabel('x') plt.ylabel('f(x)') plt.plot(x,y,'ro'); plt.grid() plt.show() ` |
Discussion
Avantages
L’interpolation au plus proche nécessite peu de calculs pour estimer la fonction en un point.
La seule mémoire nécessaire est celle pour stocker les vecteurs $x$ et $y$.
Inconvénients
L’interpolant n’est pas continu, alors que c’est souvent souhaitable dans les applications usuelles (physique, ingénierie, …).
Quand l’utiliser ?
Il y a assez peu de cas d’utilisation. Wikipédia fait mention du rendu d’images 3D.