- géobrève #2 - Quelle différence entre technopôle et technopole ?
- Un peu d'improvisation au clavier ?
Aujourd’hui, nouveau dessin « sentimental » comme le précédent. Il ne porte pas sur un théorème en particulier mais plutôt sur un tableau de sensations.
Le dessin
Sans plus attendre, voici le dessin.
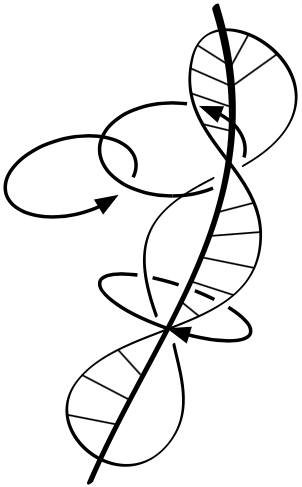
Vous noterez que je l’ai nommé « formule de Wu ». Cela n’est pas sans raison.
Légende
Ce dessin intervient dans un exposé sur une formule de Wu en dimension 3. Cette formule est la suivante :
Ce qu’il faut observer, c’est que si la quantité $w_2$ s’annule alors le membre de gauche aussi (la fonction ${\rm Sq}^1$ est un morphisme de groupes abéliens et envoie donc $0$ sur $0$) et donc $w_3 = 0$.
En ajoutant à cette formule l’hypothèse $w_1=0$, on obtient trivialement que ${\rm Sq}^1(w_2)=0$ si, et seulement si, $w_3=0$. C’est ce que ce dessin représente.
La première boucle en bas représente l’objet $w_1$ (qui a une signification géométrique précise pouvant être assimilé à la façon dont se tort un objet). Les deux autres boucles qui sont dépendantes entre elles représentent $w_2$ et $w_3$. La boucle attaché à l’objet principal est $w_2$, et vous constatez que si l’on fait disparaitre $w_2$ (c’est-à-dire si on l’annule) alors $w_3$ tombe aussi (c’est-à-dire s’annule). Et si on fait tomber $w_3$ alors $w_2$ a des chances de tomber mais sans que ça soit non plus nécessaire (ce qui revient à dire que ${\rm Sq}^1(w_2)=0$).
 Maths en images #4
Maths en images #4


