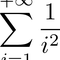- L'entre-soi et les boucles à rétroaction positive dans la gestion de projet
- Une étude de l'attractivité de Zeste de Savoir : le cas des auteurs
La programmation avec des nombres à virgule flottante est plus subtile qu’on ne pourrait le croire quand on commence à s’en servir. La première subtilité qu’on apprend est que quand on stocke 0.1 sous la forme d’un nombre flottant, on n’obtient qu’une approximation. Une autre subtilité (peut-être moins connue ?) est que la somme de nombres flottants n’est pas associative, c’est-à-dire que l’ordre utilisé peut changer le résultat. Voyons un exemple concret.
En Mathématiques, une série est une somme dont on cherche en général à connaître la limite quand le nombre d’opérations tend vers l’infini. Un des résultats connus porte sur un cas particulier des séries de Riemann :
Supposons maintenant qu’on veuille réaliser ce calcul par ordinateur : on pourra évaluer sa précision en regardant à quel point on s’approche de $\frac{\pi^2}{6}$. Je vais utiliser ici le langage Rust pour l’implémentation. C’est un langage moderne qui a l’avantage de rendre explicite le type de nombre flottants qu’on manipule. Une implémentation naïve serait la suivante :
1 2 3 4 5 6 7 8 9 | fn main() { let mut sum = 0f32; // sum est de type float32, on commence à zéro for i in 1..10.pow(8) { let f = i as f32; sum += 1.0/(f*f); } println!("résultat : {:.12}", sum); // afficher le résultat avec 12 chiffres après la virgule } |
Mais ce choix n’est pas optimal. En effet, on ajoute des nombres de plus en plus petits : d’abord $1 \times 10^0$, et finalement $1 \times 10^{-16}$. Or, pour un exposant donné, un nombre flottant codé sur 32 bits ne peut retenir que 6 à 9 chiffres corrects après la virgule. Donc toute l’information qui arrive après $10^{-9}$ est perdue. Une meilleure méthode est donc de calculer les termes de la série en commençant par le plus petit (ici $10^{-16}$). On ne perd pas d’information en stockant ce nombre, parce que l’exposant va augmenter petit à petit, et les chiffres après la virgule contiendront le plus d’information possible. Comparons ces deux méthodes :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | use std::f32; fn main() { let pi = f32::consts::PI; let correct = pi * pi / 6.0f32; let mut frombig = 0f32; for i in 1..10u32.pow(8) { let f = i as f32; // il faut convertir i en nombre flottant frombig += 1.0/(f*f); } let mut fromsmall= 0f32; for i in (1..10u32.pow(8)).rev() { // .rev() permet de commencer par la fin let f = i as f32; fromsmall+= 1.0/(f*f); } let fromsmallerror = correct - fromsmall; let frombigerror = correct - frombig; println!("valeur correcte : {:.12}", correct); println!("version naïve : {:.12} (erreur {})", frombig, frombigerror); println!("version inverse : {:.12} (erreur {})", fromsmall, fromsmallerror); println!("la version inverse est {} fois plus précise", frombigerror/fromsmallerror); } |
Après un rustc -O main.rs, mon ordinateur (qui est très lent) donne cette sortie après 300ms :
1 2 3 4 | valeur correcte : 1.644934177399 version naïve : 1.644725322723 (erreur 0.00020885468) version inverse : 1.644934058189 (erreur 0.00000011920929) la version inverse est 1752 fois plus précise |
On se rend compte qu’avec la version naïve, seulement trois chiffres après la virgule sont corrects, alors qu’avec la version inverse, on en obtient 6 ! On ne peut donc probablement pas faire mieux en restant sur des flottants codés sur 32 bits.
C’était rigolo et/ou intéressant, non ? Pour aller plus loin, quelques liens :
- Quand la calculatrice nous trompe par Aabu (merci pour sa correction par commentaire !)
- Contrôler la propagation des erreurs de calculs numériques par KFC
- Les nombres flottants logarithmiques publié lui-aussi sur ZdS
- La somme compensée de Kahan qui résoud le même problème sans devoir réordonner manuellement les opérations comme on vient de le faire ici
Merci d’avoir lu !