Aaaah, l’ordinateur quantique… Que n’entendons-nous pas parler de lui ! Outil de science-fiction pour les uns, révolutionnaire technologie d’avenir pour les autres, on entend souvent parler de lui comme la prochaine génération d’ordinateurs. Et bien sûr, on entend souvent plein d’âneries à ce sujet.
Dans ce billet, je vous propose d’explorer, en termes simples, ce qu’est l’ordinateur quantique, et surtout ce qu’il n’est pas. Comme ça, vous éviterez une crise cardiaque au prochain informaticien quantique que vous rencontrerez1 !
Comme son nom l’indique, l’ordinateur quantique repose sur la mécanique quantique. Alors qu’un ordinateur classique n’utilise que des $0$ et des $1$, un ordinateur quantique va s’appuyer sur une propriété très précise d’un objet quantique, par exemple2 le spin3 d’un électron. Ce spin, quand on l’observe, ne peut prendre que deux valeurs, qu’on associera à $0$ et $1$ : on appelle ça un qubit4. Là où ça devient intéressant, c’est que la théorie quantique nous garantit qu’avant d’observer l’électron, son spin peut être une superposition de $0$ et de $1$ : autrement dit, il est un peu des deux, sans être tout à fait l’un, ni tout à fait l’autre. Et quand on observe ce qubit, il prendra aléatoirement une valeur, soit $0$ soit $1$.
Par exemple, observons l’état quantique $\frac 1 {\sqrt{3}} \lvert 0 \rangle - \sqrt{\frac 2 3} \lvert 1 \rangle$. Cette formule barbare signifie simplement que quand on observera notre qubit (actuellement dans une superposition de $0$ et $1$), il y aura $\left(\frac 1 {\sqrt{3}}\right)^2 \approx 0.33 = 33\%$ de chances qu’on observe un $0$, et $\left(- \sqrt{\frac 2 3}\right)^2 \approx 0.67 = 67\%$ de chances qu’on observe un $1$.
Grâce à ce phénomène, un ordinateur quantique peut avoir en mémoire une configuration quantique qui explore l’ensemble des configurations possibles, et ce, en même temps. Ainsi, si l’on dispose de $n$ qubits, on peut avoir en mémoire $2^n$ états différents, soit beaucoup d’états. C’est par exemple le cas de la configuration précédente : avec 1 qubit, on avait en même temps les 2 états possibles, $0$ et $1$. Si on avait 10 qubits, on pourrait explorer les $2^{10} = 1024$ états possibles en même temps, etc. Un ordinateur classique, lui, ne pourrait explorer qu’un seul état possible à la fois.
Mais attention ! On entend souvent qu’un ordi quantique est plus rapide justement parce qu’il explore toutes ces configurations en même temps ; c’est complètement faux. Rappelez-vous que quand on observera nos qubits, le résultat sera un et un seul des états possibles, choisi aléatoirement : c’est ce qu’on appelle la réduction du paquet d’ondes.
Alors, quel est l’intérêt d’un ordinateur quantique, s’il ne peut que donner des réponses aléatoires ? Eh bien, en faisant très attention à la manière dont on manipule les qubits, on peut faire en sorte que l’ordinateur donnera quasiment toujours (voire toujours) la bonne réponse. On fait en sorte que les mauvaises réponses interfèrent entre elles, ne laissant plus la place qu’aux bonnes réponses, qui seront donc les sorties les plus probables lors de l’observation.
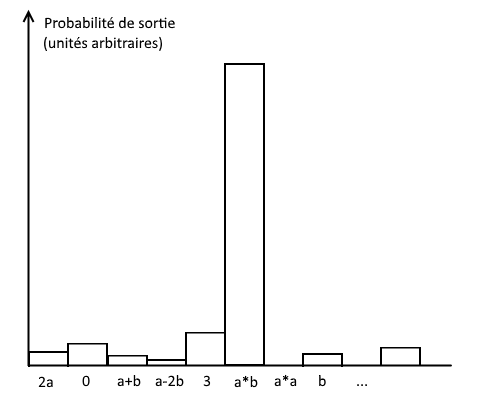
Alors, pourquoi est-ce plus rapide qu’un ordinateur classique ? Eh bien… ça ne l’est pas toujours. A l’heure actuelle, on ne connaît qu’un nombre restreint (en anglais) de problèmes pour lesquels un algorithme quantique donnerait plus vite la réponse qu’un algorithme classique. Le problème, c’est que les algorithmes quantiques sont très difficiles à trouver, et sont fondamentalement différents dans leur conception des algorithmes classiques.
Mais je m’en voudrais de vous quitter sans vous donner d’exemple concret. Prenons par exemple le problème de la factorisation d’entiers5. A l’heure actuelle, les meilleurs algorithmes classiques sont de type sous-exponentiels : c’est lent. Il existe un algorithme quantique, l’algorithme de Shor, qui est cubique : c’est beaucoup plus rapide.
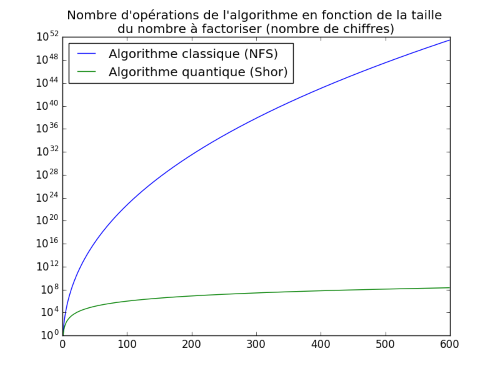
Cet algorithme, s’il venait à être implémenté sur un ordinateur quantique, sonnerait le glas du cryptosystème RSA. Une variante de l’algorithme de Shor achèverait également le problème du logarithme discret, lui aussi central en cryptographie. En bref, si l’ordinateur quantique venait au monde, alors deux des méthodes cryptographiques les plus utilisées deviendraient caduques. Rassurez-vous, les cryptologues ont déjà trouvé des cryptosystèmes qui devraient résister à l’ordinateur quantique : on parle alors de cryptologie post-quantique. En revanche, changer l’ensemble des protocoles en usage serait un véritable cauchemar.
Mais où en est-on à l’heure actuelle, avec ces fameux ordi quantiques ? Eh bien, en 2012, des chercheurs d’IBM ont implémenté, sur un ordinateur quantique, cet algorithme de Shor, et ont ainsi réussi à factoriser… $21$. Le principal problème de l’ordinateur quantique, c’est qu’à l’heure actuelle on ne peut l’utiliser qu’avec quelques qubits : plus on veut de qubits, et plus le protocole expérimental devient casse-tête. C’est notamment sur ce sujet que de nombreux chercheurs travaillent d’arrache-pied6. Ainsi, plus récemment, IBM a annoncé la réalisation d’un ordinateur quantique prototype de 50 qubits. Ça ne semble toujours pas beaucoup, mais on se demande sérieusement si cet ordinateur quantique ne sera pas plus puissant que les supercalculateurs classiques sur certains problèmes. Affaire à suivre !
Autre "détail", pour pouvoir fonctionner, les ordinateurs quantiques demandent d’être refroidis à des températures proches du zéro absolu (-273,15°C). Autrement dit, l’informatique quantique à domicile, ce n’est pas pour demain, mais ça promet quand même plein de trucs rigolos7.
-
Comme quoi, Zeste de culture sauve des vies ! Si vous aimez vos informaticiens quantique, faites tourner ce billet au maximum. La Science vous remercie. ↩
-
Il y a à l’heure actuelle plein d’autres possibilités (en anglais). Comme la recherche dans le sujet en est encore à ses balbutiements, on ne sait pas ce qui est le mieux. ↩
-
Pas besoin de savoir ce que c’est, dites-vous juste que c’est une propriété de l’électron, comme le sont sa masse, sa vitesse… ↩
-
Prononcez "cubitte". ↩
-
Le problème de factorisation est le suivant : pour un nombre $N$, quels sont ses diviseurs (plus exactement ses diviseurs premiers) ? Par exemple, $143 = 11 \times 13$. Ce problème est central en cryptographie, il est notamment à la base du cryptosystème RSA, mondialement utilisé, jusque dans votre navigateur web ou votre carte bleue : si on sait factoriser rapidement, alors RSA est cassé ! ↩
-
Alors évidemment, sur des nombres aussi petits que 21 ce n’est pas intéressant, mais c’est en persévérant qu’on réussit : en 1945, un des premiers ordinateurs, l’ENIAC, ne faisait que 357 opérations à la seconde. De nos jours, n’importe quel téléphone calcule presque 100 000 000 d’opérations dans le même intervalle. ↩
-
Je mets ici en vrac 2 infos : un ordinateur quantique peut émuler un ordinateur classique (en anglais), ce qui signifie qu’en théorie, dans le futur l’ordinateur quantique pourrait complètement remplacer l’ordinateur classique. Par ailleurs, pour les plus matheux d’entre vous, sachez que si les ordis quantiques sont plus puissants que les machines de Turing, a priori ils ne sont pas équivalents à des machines de Turing non déterministes (on pense que ces dernières sont bien plus puissantes que les ordis quantiques (en anglais)). ↩




