Dans le cadre de mon travail j’ai été amené à écrire un petit texte qui explique mon quotidien fait de "recherche (scientifique) en langages de programmation". Je me permets de le diffuser ici au cas où ça intéresse des gens.
Ma recherche
Je travaille à l’INRIA, un institut public français de recherche en informatique. Je fais de la programmation et de la recherche sur les langages de programmation.
Mon rôle est d’étudier ces langages, de mieux les comprendre, pour identifier les propriétés désirables et capturer des éléments de langage qui sont les plus simples, performants et sûrs à utiliser. Cela permet faire évoluer les langages déjà existants, voire même de créer un langage où il est plus facile de dire à la machine ce que l’on veut qu’elle fasse, et où la machine est aussi mieux capable de vérifier que notre demande est cohérente.
(Pour plus d’information sur l’étude mathématique des langages de programmation, voir le précédent billet Pourquoi la recherche en langages de programmation ?.)
Ma recherche est aussi liée au développement des assistants de preuve, des outils qui permettent non pas d’écrire des programmes et de les faire faire exécuter par l’ordinateur, mais d’écrire des preuves mathématiques et de les faire vérifier par l’ordinateur. L’interaction entre langages de programmation et assistants de preuves est double. D’une part, beaucoup de travaux sur les langages de programmation peuvent être réutilisés pour comprendre les « langages de preuve » des assistants de preuve. D’autre part, nous essayons de concevoir des langages dans lesquels on puisse donner une spécification du comportement de son programme, et aider ensuite l’ordinateur à vérifier, à prouver que la spécification est vérifiée par le programme – ces langages intègrent donc des outils de recherche de preuve et d’assistance à la preuve.
L’équipe de recherche dans laquelle je travaille, nommée Parsifal, étudie la théorie de la démonstration, c’est-à-dire l’étude formelle des preuves mathématiques. Certains mathématiciens étudient les nombres, les événements aléatoires ou les surfaces géométriques, nous étudions les preuves mathématiques elles-mêmes comme des objets formels. C’est un sujet essentiel pour comprendre la recherche de preuve, les assistants de preuve, mais qui a aussi des applications nombreuses pour étudier les langages de programmation : en regardant d’une certaine façon peut voir qu’un « programme » est aussi une « preuve » et inversement. J’utilise cette correspondance preuves-programmes dans mon travail et j’espère continuer à la développer.
Mon quotidien
Au jour le jour, ma façon de travailler ressemble à celle des mathématiciens et mathématiciennes : j’essaie de comprendre quels résultats je veux établir, et ensuite comment les prouver. Un article scientifique dans mon domaine commence typiquement par expliquer un problème perçu dans un langage de programmation donné, une proposition de solution, puis donner une définition mathématique du langage corrigé, et montrer un théorème qui nous convainc que le problème n’est plus présent. Souvent, on ne travaille pas sur un langage existant en entier, mais sur une version simplifiée, conçue pour garder uniquement les aspects que nous souhaitons étudier.
Bref, je peux présenter mon travail de recherche avec des définitions, des lemmes et des théorèmes. Mais souvent je vais aussi essayer d’implémenter les langages et les programmes considérés, pour pouvoir exécuter des exemples sur un ordinateur, comprendre certaines propriétés de l’exécution, et aussi garder un lien de praticien avec l’activité de programmation que j’étudie.
Concrètement, vous pouvez voir sur les images ci-dessous à quoi ressemble une session de travail sur Abella, un nouvel assistant de preuve en cours de développement au sein de l’équipe Parsifal. On voit à gauche une zone bleue qui représente la partie déjà vérifiée par l’outil (les preuves dans cette partie sont correctes), une zone noire qui n’a pas encore été vérifiée (on est en train d’écrire la preuve), et à droite on voit le "but" courant, ce qu’il reste à faire vérifier pour conclure la preuve :
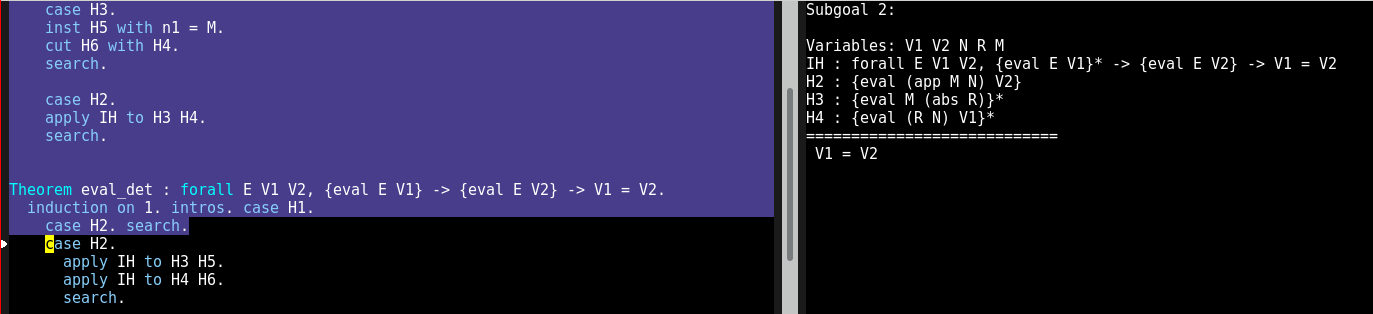
Les assistants de preuve ont vocation à être utilisés par tous les scientifiques faisant des raisonnement mathématiques, mais il reste du travail pour qu’ils soient plus faciles à utiliser – ils sont aujourd’hui réservés aux spécialistes du domaine. Ma communauté de recherche fait des efforts pour adopter ces outils, je m’en sers parfois pour valider mon propre travail, et cela permet de découvrir des problèmes d’utilisation, des points à améliorer pour pouvoir espérer une adoption plus grande. Aujourd’hui quand quelqu’un annonce un nouveau résultat mathématique, il peut être très difficile de savoir si le résultat est correct ou non ; il sera peut-être un jour réaliste de demander à la personne de fournir une preuve vérifiée par un assistant de preuve, pour accélérer son étude et sa compréhension par les scientifiques du domaine.
Échanger avec l’extérieur
De nouveaux langages de programmation apparaissent tous les ans. Une partie est construite par des scientifiques du domaine, ou des gens qui ont étudié notre travail, mais la majorité vient de personnes spécialistes d’un tout autre domaine de la programmation, qui veulent créer un bon langage pour leurs besoins, sans avoir étudié la théorie.
Une partie de notre travail consiste donc à entrer en contact avec les personnes qui créent de nouveaux langages et les utilisent, pour leur transmettre de bonnes pratiques de conception, les alerter sur des problèmes à venir, et aussi découvrir de leurs besoins et idées pour faire évoluer notre compréhension commune des langages de programmation. Nous avons parfois des discussions directes avec l’équipe qui conçoit un langage, et il nous arrive même de travailler scientifiquement sur ces nouveaux langages (récemment ma communauté s’est penchée sur les langages R, Ceylon, Rust et Julia par exemple), mais nous avons aussi un impact indirect, en faisant utiliser des langages conçus par notre communauté dont certaines idées inspirent ensuite les nouveaux langages de programmation. Étudier les nouveaux langages de non-spécialistes nous permet aussi de découvrir de nouveaux besoins qui viennent enrichir notre activité de recherche.
Ainsi, je travaille sur le langage de programmation OCaml (comme scientifique et aussi comme contributeur et co-mainteneur de l’implémentation), conçu à l’INRIA et encore développé en grande partie dans l’institut. Le langage est utilisé dans des projets venant de tous les horizons, la recherche, le logiciel libre et l’industrie, qui font connaître ses idées à un public plus large. L’idée de programmation « fonctionnelle », mettant l’accent sur l’importance de raisonner rigoureusement sur son code, est promue par OCaml mais aussi d’autres langages comme Scala, Haskell, ou le langage F# (dérivé de OCaml), et influence les évolutions de langages grand public comme Java, C# ou Javascript.
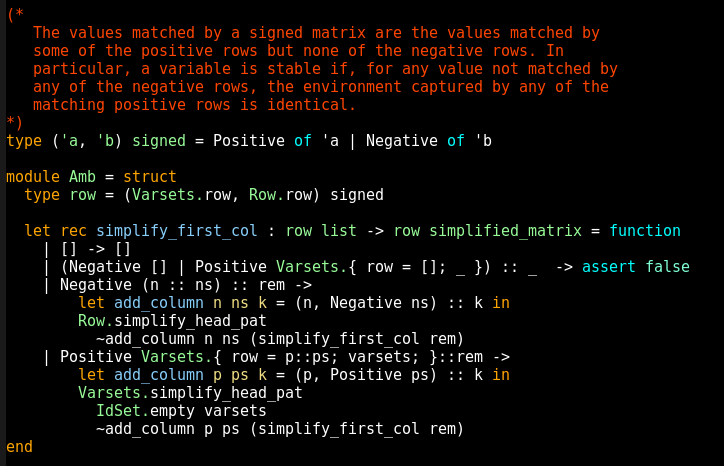
Recherche et logiciel libre
Les résultats de mes travaux sont accessibles à tous – pour moi c’est une part essentielle du contrat moral de la recherche publique. Mes publications sont en accès libre (et archivées sur arXiv et/ou HAL (si possible en licence CC-BY, mais malheureusement ce n’est pas toujours moi qui décide), et le logiciel produit est sous licence libre.
Dans le cadre de mon activité de recherche, je produis surtout des petits prototypes qui ne sont pas forcément très intéressants pour les autres – même s’il m’arrive de partager effectivement du code avec d’autres chercheurs ou de collaborer sur leurs projets. Mon activité de développement principale tourne autour de l’implémentation du langage OCaml, et d’outils et bibliothèques de son écosystème (je travaille là-dessus dans une zone assez floue entre le temps libre/personnel et le temps de travail).
Le compilateur OCaml est un logiciel libre, et j’essaie (ainsi que les autres mainteneurs) de faire des efforts pour encourager les contributions externes – faire des revues de code pour les contributeurs externes, marquer des bugs comme "faciles" sur le bugtracker, organiser des réunions d’initiation à la contribution.
Un langage de programmation qui a des utilisateurs n’est pas un projet libre facile à gérer : il faut être très prudent quand on accepte de nouvelles fonctionnalités pour préserver la compatibilité arrière et éviter l’enfouissement sous les fonctionnalités (feature bloat). Du coup il peut être très difficile de juger des propositions de changement et de prendre des décisions, ce qui frustre les contributeurs. Une nouvelle fonctionnalité peut attendre dans un coin pendant des années parce qu’elle n’est "pas complète", voire même parce qu’il y a deux propositions de syntaxe différentes et qu’on ne sait pas laquelle on préfère. Ce n’est pas unique à OCaml; tout langage est beaucoup plus difficile à évoluer qu’il n’y paraît au premier abord. C’est une raison de plus de bien faire attention à la théorie quand on conçoit un langage ou une nouvelle fonctionnalité, pour essayer d’avoir la meilleure première version possible 
Ces derniers temps j’ai aussi eu l’occasion de faire un peu de gestion des publications de nouvelle version (release management), à l’occasion en particulier d’un congé parental pris par le gestionnaire de nouvelles versions habituel, Damien Doligez. Le plus difficile dans cette partie du travail est de décider comment réagir en cas de problème repéré tard dans le cycle de développement, et d’évaluer la sûreté et les risques pour la compatibilité arrière des correctifs proposés – un correctif risque toujours d’introduire de nouveaux problèmes.



 .
.