Il y a deux ans, je célébrais Noël avec 10 amis et nous avions décidé de s’offrir des cadeaux et pour ce faire, nous avons organisé un "Secret Santa". Pour ceux qui ne connaissent pas Secret Santa, l’idée est très simple : avant Noël, un père Noël secret est attributé à chaque invité. Ce père Noël aura la tâche de trouver un cadeau pour cette personne et de lui offrir lors de la fête de Noël. Le jour du réveillon, on choisit une personne au hasard et celle-ci offre son cadeau à la personne qui lui a été attribuée puis cette personne fait de même et ainsi de suite.
Donc, comme je le disais, nous avions décidé d’organiser un Secret Santa mais il s’est passé quelque chose d’horrible: il y avait une sous-boucle dans la distribution ! J’ai commencé en donnant mon cadeau à une personne A qui a continué en donnant son cadeau à une personne B qui a continué en donnant son cadeau à… moi. Cela signifiait donc qu’on allait devoir choisir une autre personne au hasard pour continuer la distribution entre les 7 personnes restantes.
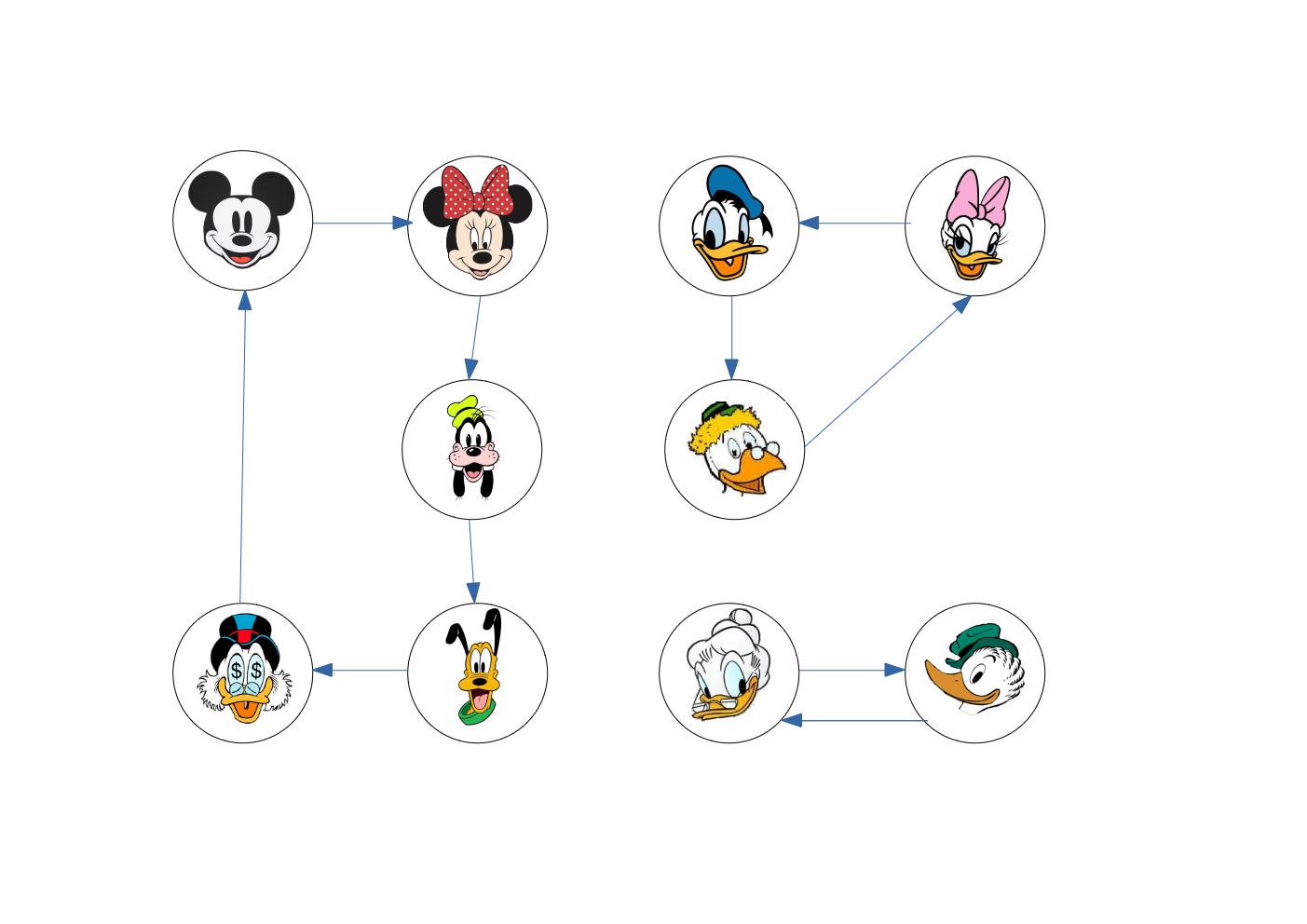
L’année dernière, j’ai décidé de ne pas laisser cette situation se reproduire. Voyons comment écrire une application qui attribue des pères Noëls secrets à l’aide de notre meilleure amie: les mathématiques.
Ce que nous disent les maths
La théorie des graphes
Une discipline passionnante des maths est la théorie des graphes. Elle permet de représenter des problèmes complexes sous forme de graphes.
Un graphe, c’est une structure, orientée ou non, composée de sommets et d’arêtes. Un exemple typique est d’utiliser un graphe pour représenter des voyages possibles entre destination. Dans ce cas, les sommets sont des villes et les arêtes représentent s’il est possible de se rendre de façon direct de la ville A à la ville B. Ceci est représenté dans l’illustration ci-dessous.
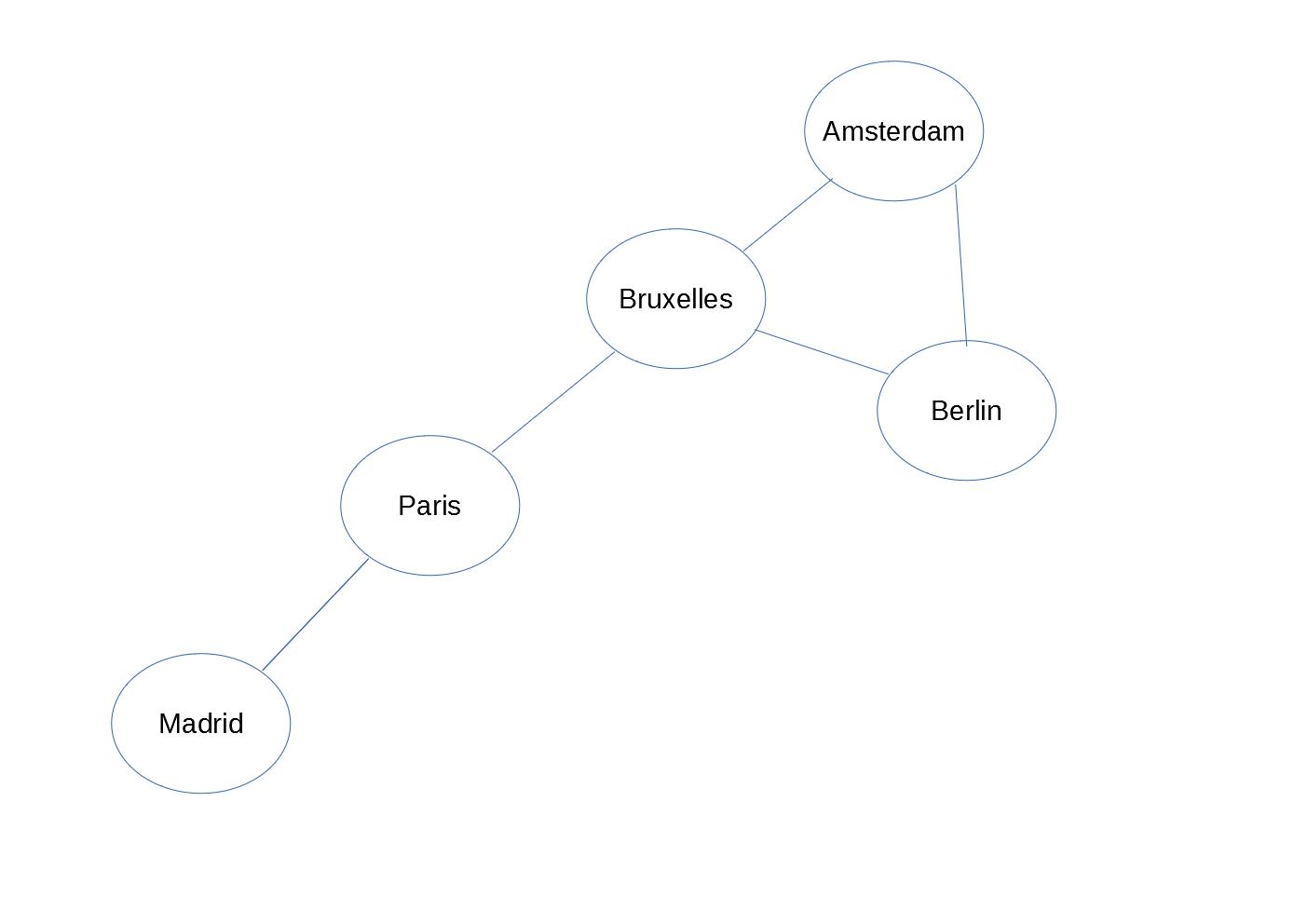
Dans cet exemple, il est possible de se rendre directement de Paris à Madrid mais pas de Paris à Berlin. Pour ce faire, il faut d’abord transiter par Bruxelles. Il est également possible de donner une valeur aux arêtes. Dans notre exemple, cela pourrait représenter la distance entre les villes. Ensuite, nous pourrions essayer de trouver le chemin le plus court entre deux villes.
Comme mentionné plus haut, une graphe peut être orienté ou non-orienté. L’exemple des villes est non-orienté : une arête existe entre Paris et Bruxelles, cela signifie qu’il est possible de se rendre de Paris à Bruxelles mais également de faire le chemin inverse, de Bruxelles à Paris. On pourrait imaginer rendre ce graphe orienté, ce qui représenterait des routes à sens unique par exemple.
Très bien, maintenant que nous avons un peu discuter de la théorie, essayons de l’appliquer à notre cas. Pour le Secret Santa, nos sommets seront les participants et les arêtes représenteront l’acte de donner un cadeau à quelqu’un. Il s’agira donc d’un graphe orienté car on veut savoir qui est la personne qui donne le cadeau et qui est celle qui le reçoit. Enfin, on ne donnera aucun poids à nos arêtes étant donné qu’on donne toujours un cadeau ou non. On ne donne jamais de demi-cadeau.
Hamilton à la rescousse
Des nombreux mathématiciens se sont intéressés aux graphes et celui qui va nous être utile ici est William Rowan Hamilton. En effet, un graphe est dit hamiltonien si il possède un cycle hamiltonien. Un cycle hamiltonien peut être décomposé en deux parties:
- Cycle: Un chemin est considéré comme un cycle si le sommet duquel le chemin débute est également celui auquel il se termine
- Hamiltonien: un chemin est hamiltonien s’il ne passe qu’une et une seule fois par chaque sommet
La bonne nouvelle, c’est qu’il s’agit exactement de ce que nous voulons! On veut que notre chemin implique tous les participants et ceux-ci ne doivent donner (et recevoir) qu’un seul cadeau. La mauvaise, c’est qu’il n’existe pas d’algorithme qui permette de trouver ce cycle hamiltonien en un temps polynomial.
Implémentation
Représentation du graphe
Maintenant que nous connaissons la théorie, voyons comment nous pouvons implémenter une solution en commençant pas la représentation. Une méthode typique pour représenter un graphe dirigé est d’utiliser un array tab à 2 dimensions où la valeur tab[x][y] représente si une arête existe depuis x vers y. Dans notre cas, nous utiliserons deux valeurs:
-
POSSIBLEsi une arête peut être tracée de x vers y -
IMPOSSIBLEsi il n’existe pas d’arêtes de x vers yCeci est représenté dans l’image ci-dessous où une case blanche représente l’état
POSSIBLEet une case rouge l’étatIMPOSSIBLE.

La diagonale est uniquement composée d’états impossible car personne ne peut être son propre Secret Santa. J’ai aussi ajouté une contrainte que les couples ne peuvent pas être le Secret Santa l’un de l’autre afin d’ajouter quelque contraintes (et je trouvais cela plus amusant). On pourrait très bien imaginer plus ou moins de contraintes (par exemple, si Donald était le Secret Santa de Pluto l’année dernière, on pourrait l’interdire cette année).
Trouver un cycle hamiltonien
Place maintenant à l’algorithme en tant que tel. Comme mentionné plus tôt, il est impossible de trouver un cycle hamiltonien en un temps polynomial. Il existe des algorithmes optimisés qui permettent de limiter le temps nécessaire à sa résolution mais si l’on se limite à un nombre limité d’amis avec qui passer Noël, une simple approche exhaustive fera l’affaire, d’autant plus que notre graphe comporte énormément d’arêtes.
Voici donc notre approche:
- Choisir un sommet au hasard, l’ajouter au cycle. Il s’agit de notre sommet de départ
- Pour ce sommet, choisir aléatoirement un autre sommet accessible.
- Ajouter ce nouveau sommet au cycle:
- Si ce sommet a déjà été visité, le retirer du cycle et retourner à l’étape 2.
- Si il n’a pas encore été visité et qu’il s’agit du dernier sommet, c’est terminé on a trouvé notre cycle.
- Sinon, répéter l’étape deux à partir du nouveau sommet
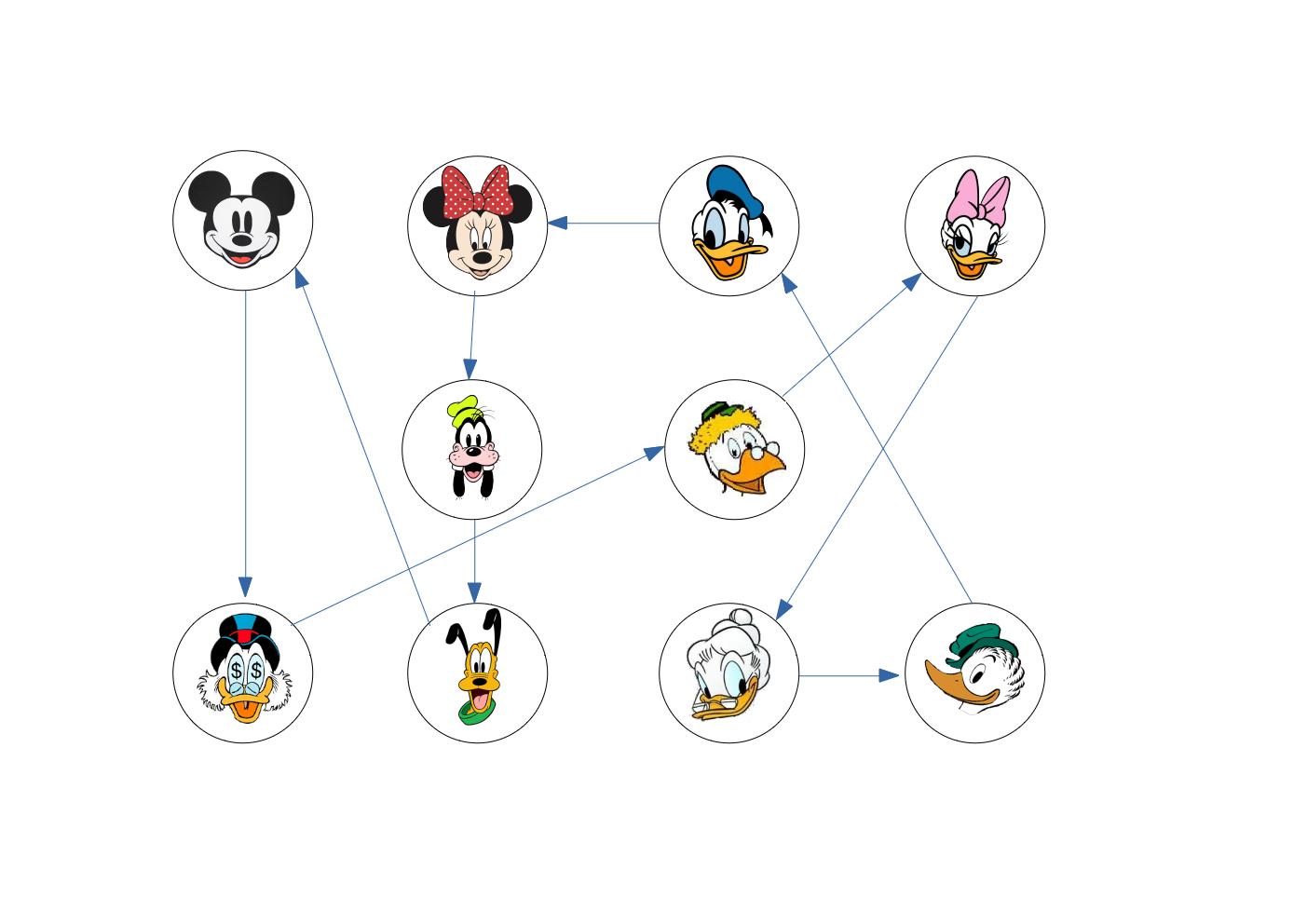
Exemple en Java
Voyons un exemple d’une implémentation en Java.
public class Participant {
private String name;
private List<String> exclusionList;
//...
}
public class SecretSantaService {
public enum Status {
Possible,
Impossible,
;
}
public List<Participant> computeHamiltonCycle(List<Participant> participants) {
Map<Participant, Map<Participant, Status>> giftsTable = buildGiftsTable(participants);
ArrayList<Participant> hamiltonCycle = new ArrayList<>();
hamiltonCycle.add(participants.get(0));
if (!computeHamiltonCycle(giftsTable, hamiltonCycle, participants.get(0))) {
throw new IllegalArgumentException("Could not compute a proper secret santa based on provided participants");
}
return hamiltonCycle;
}
private Map<Participant, Map<Participant, Status>> buildGiftsTable(List<Participant> participants) {
Map<Participant, Map<Participant, Status>> giftsTable = new HashMap<>();
for(Participant givingParticipant : participants) {
Map<Participant, Status> statusMap = new HashMap<>();
for(Participant receivingParticipant : participants) {
if (givingParticipant.getExclusionList() != null && givingParticipant.getExclusionList().contains(receivingParticipant.getName())) {
statusMap.put(receivingParticipant, Status.Impossible);
} else {
statusMap.put(receivingParticipant, Status.Possible);
}
}
giftsTable.put(givingParticipant, statusMap);
}
return giftsTable;
}
private boolean computeHamiltonCycle(Map<Participant, Map<Participant, Status>> giftsTable, List<Participant> hamiltonCycle, Participant givingParticipant) {
if(hamiltonCycle.size() == giftsTable.keySet().size() && giftsTable.get(givingParticipant).get(hamiltonCycle.get(0)) == Status.Possible) {
//We are done
return true;
}
List<Participant> possibleReceivingParticipants = getPossibleReceivingParticipants(giftsTable.get(givingParticipant), hamiltonCycle);
while(possibleReceivingParticipants.size() > 0) {
int receivingParticipantIdx = getRandomNumberInRange(0, possibleReceivingParticipants.size() - 1);
Participant receivingParticipant = possibleReceivingParticipants.get(receivingParticipantIdx);
hamiltonCycle.add(receivingParticipant);
if (computeHamiltonCycle(giftsTable, hamiltonCycle, receivingParticipant)) {
return true;
}
hamiltonCycle.remove(receivingParticipant);
possibleReceivingParticipants.remove(receivingParticipantIdx);
}
return false;
}
private List<Participant> getPossibleReceivingParticipants(Map<Participant,SecretSantaService.Status> receivingParticipants, List<Participant> hamiltonCycle) {
return receivingParticipants.entrySet()
.stream()
.filter(e -> e.getValue() !=SecretSantaService.Status.Impossible && !hamiltonCycle.contains(e.getKey()))
.map(Map.Entry::getKey)
.collect(Collectors.toList());
}
private int getRandomNumberInRange(int min, int max) {
if(min == max) {
return min;
}
if (min > max) {
throw new IllegalArgumentException("max must be greater than min");
}
Random r = new Random();
return r.nextInt((max - min) + 1) + min;
}
}
Tout commence par un appel à la méthode computeHamiltonCycle(List<Participant> participants) à laquelle on passe une liste de Participants. Chaque Participant est constitué d’un nom et d’une liste d’exclusions (afin d’exclure les couples par exemple).
La méthode computeHamiltonCycle(List<Participant> participants) va tout d’abord créer notre graphe (giftsTable) sur base des Participants reçus puis va appeler la méthode computeHamiltonCycle(Map<Participant, Map<Participant, Status>> giftsTable, List<Participant> hamiltonCycle, Participant givingParticipant) en lui fournissant le graphe fraichement créé, une le cycle hamiltonien (initialement uniquement composé du sommet de départ) ainsi que le premier participant duquel le cycle débutera.
Dans cette nouvelle méthode, on vérifie tout d’abord si on n’a pas déjà atteint la fin de notre calcul. Évidemment, pour la première itération, c’est un peu inutile mais comme nous allons avoir des appels récursifs, cela servira de condition d’arrêt.
Ensuite, on choisit une arête au hasard dans les arêtes disponibles ayant un sommet pas encore visité et on la suit afin d’atteindre le prochain sommet. On appelle alors notre méthode à nouveau en utilisant ce nouveau sommet. Si cet appel échoue (retourne false), on retire le sommet du cycle et on en choisit un autre aléatoirement.
Enfin, une fois que notre chemin est de longueur égale au nombre de participants, on vérifie que nous pouvons bien "fermer" le cycle en vérifiant que notre dernier sommet a le droit de donner un cadeau au sommet initial. Si c’est le cas, notre algorithme est terminé et nous avons trouvé notre cycle hamiltonien.
Créer un webservice
Afin de partager ce service avec le monde afin d’éviter à tous d’avoir des Secret Santa non-optimaux, on peut facilement utiliser Spring Boot et créer un Controller appelant notre service.
@Controller
@RequestMapping("/")
public class SecretSantaController {
private final SecretSantaService secretSantaService;
public SecretSantaController(SecretSantaService secretSantaService) {
this.secretSantaService = secretSantaService;
}
@RequestMapping(method= RequestMethod.GET)
public SecretSantaResponse getSecretSanta(SecretSantaRequest request) {
var hamiltonCycle = secretSantaService.computeHamiltonCycle(request.getParticipants());
List<SecretSanta> secretSantas = buildSecretSantas(hamiltonCycle);
return new SecretSantaResponse(secretSantas);
}
private List<SecretSanta> buildSecretSantas(List<Participant> hamiltonCycle) {
List<SecretSanta> secretSantas = new ArrayList<>();
Participant previousParticipant = hamiltonCycle.get(hamiltonCycle.size() - 1);
for (Participant participant : hamiltonCycle) {
secretSantas.add(new SecretSanta(previousParticipant, participant));
previousParticipant = participant;
}
return secretSantas;
}
}
Un exemple de ceci est disponible à l’adresse https://secretsanta.migwel.dev/.
Test
Afin de vérifier que tout ceci fonctionne correctement, on peut écrire un test en utilisant JUnit.
@Test
void testGetValidSecretSanta() throws IOException {
InputStream inStream = this.getClass().getClassLoader().getResourceAsStream("validsecretsantarequest.json");
SecretSantaRequest request = new ObjectMapper().readValue(inStream, SecretSantaRequest.class);
SecretSantaResponse response = controller.getSecretSanta(request);
List<SecretSanta> secretSantas = response.getSecretSantas();
assertEquals(request.getParticipants().size(), secretSantas.size());
Set<Participant> givingParticipant = new HashSet<>();
Set<Participant> receivingParticipant = new HashSet<>();
Participant previousReceiver = secretSantas.get(secretSantas.size() - 1).getReceiver();
for(SecretSanta secretSanta : secretSantas) {
assertEquals(previousReceiver, secretSanta.getSecretSanta());
assertFalse(givingParticipant.contains(secretSanta.getSecretSanta()));
assertFalse(receivingParticipant.contains(secretSanta.getReceiver()));
givingParticipant.add(secretSanta.getSecretSanta());
receivingParticipant.add(secretSanta.getReceiver());
previousReceiver = secretSanta.getReceiver();
}
}
Aussi, il est important de tester que si une requête est invalide (par exemple, si un des participants ne veut donner de cadeau à personne), le service doit échouer.
@Test
void testGetInvalidSecretSanta() throws IOException {
InputStream inStream = this.getClass().getClassLoader().getResourceAsStream("invalidsecretsantarequest.json");
SecretSantaRequest request = new ObjectMapper().readValue(inStream, SecretSantaRequest.class);
assertThrows(IllegalArgumentException.class, () -> controller.getSecretSanta(request));
}
Nous voici donc prêts à aborder les fêtes de fin d’année comme il se doit, sans avoir à craindre les horribles sous-boucles de Noël. Si vous souhaitez faire tourner votre propre instance, les sources sont disponibles sur Github.


